Georgij Gamov. Priklyucheniya Mistera Tompkinsa
Mister Tompkins v Strane CHudes
Mister Tompkins issleduet atom
----------------------------------------------------------------------------
Illyustracii avtora i Dzhona Hukhema
Perevod s anglijskogo YUliya Danilova
Bibliotechka Kvant.
M., Byuro Kvantum, 1993
OCR Bychkov M.N. mailto:bmn@lib.ru
----------------------------------------------------------------------------
Predislovie
Zimoj 1938 goda ya napisal korotkij fantasticheskij s tochki zreniya nauki
(no ne nauchno-fantasticheskij) rasskaz, v kotorom predprinyal popytku
ob座asnit' dostupno dlya nespecialista osnovnye idei teorii iskrivlennogo
prostranstva i rasshiryayushchejsya Vselennoj. YA reshil, chto dlya etogo luchshe vsego
sil'no uvelichit' masshtaby real'no sushchestvuyushchih relyativistskih yavlenij i tem
samym sdelat' ih legko nablyudaemymi dlya geroya moego rasskaza - nekoego C. G.
H. Tompkinsa {Inicialy mistera Tompkinsa (v anglijskom originale) C. G. H.
Tompkins obyazany svoim proishozhdeniem trem fundamental'nym fizicheskim
konstantam: skorosti sveta s, gravitacionnoj postoyannoj G i kvantovoj
postoyannoj Planka h. CHtoby eti konstanty stali zametny cheloveku s ulicy, ih
neobhodimo vo mnogo raz uvelichit'.}, skromnogo bankovskogo sluzhashchego,
interesuyushchegosya sovremennoj naukoj.
Rukopis' ya otoslal v redakciyu zhurnala "Harper's Magazine" i, kak i vse
nachinayushchie avtory, v skorom vremeni poluchil ee obratno vmeste s uvedomleniem
ob otkaze. Poproboval bylo poslat' rukopis' v redakcii poldyuzhiny drugih
zhurnalov - rezul'tat okazalsya takim zhe. Togda ya zasunul rukopis' v yashchik
svoego pis'mennogo stola i zabyl o nej.
Letom togo zhe goda mne dovelos' pobyvat' na mezhdunarodnom kongresse po
teoreticheskoj fizike, proishodivshem v Varshave pod egidoj Ligi Nacij. Kak-to
raz ya razgovorilsya tam za stakanom prevoshodnogo pot'skogo meda s moim
davnim priyatelem serom CHarlzom Darvinom, vnukom togo samogo CHarlza Darvina
(avtora "Proishozhdeniya vidov"). Rech' zashla o populyarizacii nauki. YA povedal
Darvinu o postigshej menya neudache na poprishche populyarizacii, i tot posovetoval
mne v otvet:
- Znaete, chto ya vam skazhu, Gamov? Po vozvrashchenii v Soedinennye SHtaty
razyshchite svoyu rukopis' i poshlite ee doktoru CHarlzu Snou. On sejchas
redaktiruet nauchno-populyarnyj zhurnal "Discovery", vypuskaemyj izdatel'stvom
Kembridzhskogo universiteta.
Tak ya i postupil. A cherez nedelyu prishla telegramma ot Snou. V nej
znachilos': "Vasha stat'ya budet opublikovana v sleduyushchem nomere. Prisylajte
eshche". Vskore v vypuskah zhurnala "Discovery" odna za drugoj poyavilis' povesti
o mistere Tompkinse, v kotoryh populyarno izlagalis' teoriya otnositel'nosti i
kvantovaya mehanika. A zatem ya poluchil pis'mo ot izdatel'stva Kembridzhskogo
universiteta, v kotorom mne predlagalos', dopolniv uzhe vyshedshie stat'i
neskol'kimi novymi dlya bol'shego ob容ma, opublikovat' povesti o mistere
Tompkinse v vide otdel'noj knizhki. |ta knizhka pod nazvaniem "Mister Tompkins
v Strane CHudes" vyshla v izdatel'stve Kembridzhskogo universiteta v 1940 g. i
s teh por vyderzhala 16 izdanij. Za pervoj knizhkoj posledovalo prodolzhenie -
"Mister Tompkins issleduet atom". Vtoraya knizhka vyshla vpervye v 1944 g. i s
teh por uspela vyderzhat' 10 izdanij. Obe knizhki byli perevedeny na vse
evropejskie yazyki (krome russkogo), a takzhe - na kitajskij i hindi.
Nedavno izdatel'stvo Kembridzhskogo universiteta reshilo vypustit' obe
knizhki pod odnoj oblozhkoj i obratilos' ko mne s pros'boj obnovit' ustarevshij
material i dobavit' neskol'ko istorij o sobytiyah, kotorye proizoshli v fizike
i smezhnyh oblastyah nauki so vremeni vyhoda pervyh izdanij moih povestej.
Tak, mne prishlos' dobavit' istorii o delenii i sinteze yader, stacionarnoj
Vselennoj i uvlekatel'nyh problemah fiziki elementarnyh chastic. Ves'
material vmeste sostavil soderzhanie etoj knigi.
Ne mogu ne skazat' neskol'ko slov ob illyustraciyah. Vse illyustracii k
moim stat'yam, opublikovannym v zhurnale "Discovery", i k pervoj knizhke byli
vypolneny hudozhnikom Dzhonom Hukhemom, nadelivshim Mistera Tompkinsa
opredelennymi portretnymi chertami. Kogda ya napisal vtoruyu knizhku, mister
Hukhem udalilsya ot del i mne prishlo v golovu samomu proillyustrirovat' knizhku
v duhe Hukhema. Novye illyustracii k predlagaemoj chitatelyu knige takzhe
vypolneny mnoj. Stihi i pesenki napisany moej zhenoj Barbaroj.
Georgij Gamov
Universitet Kolorado, Boulder, shtat Kolorado, SSHA
Moemu drugu i izdatelyu Ronal'du Mensbridzhu
Vvedenie
S detstva my privykaem k okruzhayushchemu miru, kakim on vosprinimaetsya
nashimi pyat'yu chuvstvami; imenno v detstve u nas formiruyutsya fundamental'nye
predstavleniya o prostranstve, vremeni i dvizhenii. Nash razum vskore nastol'ko
osvaivaetsya s etimi ponyatiyami, chto vposledstvii my sklonny schitat'
edinstvenno vozmozhnym nashe osnovannoe na nih predstavlenie o vneshnem mire i
lyubaya mysl' ob izmenenii etih ponyatij kazhetsya nam paradoksal'noj. Odnako
razvitie tochnyh fizicheskih metodov nablyudeniya i bolee glubokij analiz
nablyudaemyh sootnoshenij priveli sovremennuyu nauku k vpolne opredelennomu
vyvodu o tom, chto ee "klassicheskie" osnovy okazyvayutsya sovershenno
nesostoyatel'nymi, kogda ih pytayutsya primenit' k podrobnomu opisaniyu yavlenij,
obychno nedostupnyh nablyudeniyam, i chto dlya pravil'nogo i neprotivorechivogo
opisaniya nashego utonchennogo opyta sovershenno neobhodimo vnesenie nekotoryh
izmenenij v fundamental'nye ponyatiya - prostranstvo, vremya i dvizhenie.
Vmeste s tem rashozhdeniya mezhdu ponyatiyami, osnovannymi na obydennom
zdravom smysle, i ponyatiyami, vvedennymi sovremennoj fizikoj, prenebrezhimo
maly, poka rech' idet o nashem povsednevnom zhitejskom opyte. No stoit lish' nam
voobrazit' inye miry, v kotoryh dejstvuyut takie zhe fizicheskie zakony, kak v
nashem sobstvennom mire, no s drugimi chislovymi znacheniyami fizicheskih
konstant, ustanavlivayushchih predely primenimosti staryh ponyatij, kak novye
(pravil'nye) predstavleniya o prostranstve, vremeni i dvizhenii, k kotorym
sovremennaya nauka prishla v rezul'tate dolgih i kropotlivyh issledovanij,
stanovyatsya dostoyaniem obychnogo zdravogo smysla. Mozhno utverzhdat', chto v
takih mirah dazhe pervobytnyj dikar' byl by znakom s principami teorii
otnositel'nosti i ispol'zoval by ih na ohote i dlya udovletvoreniya drugih
povsednevnyh potrebnostej.
Geroj istorij, s kotorymi vy poznakomites' v etoj knige, perenositsya vo
sne v neskol'ko takih mirov, gde yavleniya, obychno nedostupnye nashim chuvstvam,
usilivayutsya do takoj stepeni, chto ih mozhno nablyudat' kak sobytiya
povsednevnoj zhizni. V fantasticheskih, no vpolne real'nyh ("pravil'nyh") s
nauchnoj tochki zreniya snah nashemu geroyu pomogaet staryj professor fiziki (na
docheri kotorogo po imeni Mod nash geroj v konce koncov zhenitsya), prosto i
dohodchivo ob座asnyayushchij neobychnye yavleniya, nablyudaemye geroem v mire teorii
otnositel'nosti, kosmologii, kvantovoj mehaniki, atomnoj i yadernoj fiziki,
teorii elementarnyh chastic i t. d.
Nadeemsya, chto neobychnye puteshestviya mistera Tompkinsa pomogut
interesuyushchemusya chitatelyu sostavit' bolee yasnoe predstavlenie o tom real'nom
fizicheskom mire, v kotorom my zhivem.
Blagodarnosti
-----
Vyrazhayu svoyu priznatel'nost' Muzykal'noj korporacii |dvarda B. Marksa za
razreshenie vosproizvesti noty psalma "Prijdite, pravednye!" ("O, atom
per-r-rvichnyj!", s. 75) i gimna "Prav', Britaniya!" ("Vselennaya ne voznikla
vdrug", s. 80) iz sbornika "Vremya pet'" i izdatel'stvu Makmillana za ris. A
so stranicy 175 knigi "Kristallicheskoe sostoyanie" sera U. G. Bregga i U. L.
Bregga.
ogranichenie skorosti
 V tot den' vse banki byli zakryty - vyhodnoj, i mister Tompkins,
skromnyj sluzhashchij solidnogo gorodskogo banka, vstal pozzhe obychnogo i ne
spesha pozavtrakal. Pora bylo pozabotit'sya o dosuge, i mister Tompkins reshil,
chto bylo by neploho shodit' na dnevnoj seans v kino. Razvernuv utrennyuyu
gazetu na toj polose, gde publikovalas' informaciya o razvlecheniyah, on
uglubilsya v izuchenie repertuara kinoteatrov. Ni odin iz reklamiruemyh
fil'mov ne pokazalsya misteru Tompkinsu dostatochno privlekatel'nym. On
terpet' ne mog vsyu etu gollivudskuyu drebeden' s neskonchaemymi lyubovnymi
istoriyami, razygryvaemymi populyarnymi kinozvezdami. Vot esli by nashelsya hotya
by odin fil'm s syuzhetom, zaimstvovannym iz real'noj zhizni, byt' mozhet, s
primes'yu chego-nibud' neobychnogo ili dazhe fantasticheskogo! No takih fil'mov -
uvy! - ne bylo. Neozhidanno vnimanie mistera Tompkinsa privleklo nebol'shoe
ob座avlenie v samom uglu gazetnoj polosy. Mestnyj universitet dovodil do
svedeniya vseh zhelayushchih, chto v ego pomeshchenii budet prochitan cikl lekcij po
problemam sovremennoj fiziki. Blizhajshaya lekciya sostoitsya segodnya vecherom i
budet posvyashchena teorii otnositel'nosti |jnshtejna. Vot eto stoyashchee delo!
Misteru Tompkinsu chasten'ko prihodilos' slyshat', chto vo vsem mire edva li
dyuzhina lyudej po-nastoyashchemu ponimayut teoriyu |jnshtejna! A chto esli on, mister
Tomggkins, stanet trinadcatym? YAsnoe delo: on nepremenno otpravitsya na
lekciyu. |to kak raz to, chto emu nuzhno! Kogda mister Tompkins voshel v bol'shuyu
universitetskuyu auditoriyu, lekciya uzhe nachalas'. Vse pomeshchenie bylo bitkom
nabito studentami (v osnovnom eto byli molodye lyudi), s nepoddel'nym
interesom vnimavshimi vysokomu sedoborodomu cheloveku u doski, kotoryj pytalsya
ob座asnit' auditorii osnovnye idei teorii otnositel'nosti. Iz slov lektora
mister Tompkins ponyal tol'ko, chto osnovnoj punkt teorii |jnshtejna -
sushchestvovanie maksimal'noj skorosti - skorosti sveta, kotoruyu ne mozhet
prevzojti ni odno dvizhushcheesya material'noe telo, i chto eto obstoyatel'stvo
privodit k ves'ma strannym i neobychnym sledstviyam. Pravda, professor
zametil, chto, poskol'ku skorost' sveta sostavlyaet 300000 kilometrov v
sekundu, relyativistskie (t.e. svyazannee s teoriej otnositel'nosti) effekty
edva li mogut nablyudat'sya v yavleniyah povsednevnoj zhizni. CHto zhe kasaetsya
prirody etih neobychnyh effektov, to ponyat' ee bylo nesravnenno trudnee, i
misteru Tompkinsu pokazalos', chto vse, o chem govorit lektor, protivorechilo
zdravomu smyslu. On popytalsya myslenno predstavit' sebe sokrashchenie
izmeritel'nyh sterzhnej i strannoe povedenie chasov - effekty, kotoryh
sledovalo by ozhidat' pri dvizhenii so skorost'yu, blizkoj k skorosti sveta, no
tut golova ego medlenno sklonilas' na plecho.
Kogda mister Tompkins snova otkryl glaza, on obnaruzhil, chto sidit ne na
skam'e v universitetskoj auditorii, a na skamejkah, ustanovlennyh gorodskimi
vlastyami dlya udobstva passazhirov, ozhidayushchih avtobus. Krugom prostiralsya
krasivyj starinnyj gorodok so srednevekovymi zdaniyami kolledzhej,
vystroivshimisya vdol' ulicy. Mister Tompkins zapodozril bylo, chto vidit vse
eto vo sne, no k ego udivleniyu nichego neobychnogo vokrug ne proishodilo, dazhe
polismen, stoyavshij na protivopolozhnom uglu, vyglyadel tak, kak obychno
vyglyadyat polismeny. Strelki bol'shih chasov na bashne v konce ulicy pokazyvali
pyat' chasov, i ulicy byli pochti pustynnymi. Odinokij velosipedist pokazalsya
vdali i stal medlenno priblizhat'sya. Kogda on pod容hal poblizhe, mister
Tompkins vytarashchil glaza ot izumleniya: i velosiped, i vossedavshij na nem
molodoj chelovek byli neveroyatno sokrashcheny v napravlenii dvizheniya, kak budto
ih rassmatrivali cherez cilindricheskuyu linzu. CHasy na bashne probili pyat', i
velosipedist, po-vidimomu, kuda-to speshivshij, prinaleg na pedali. Mister
Tompkins ne zametil, chtoby skorost' ot etogo pribavilas', no usiliya
velosipedista ne proshli bessledno: on sokratilsya eshche sil'nee i otpravilsya
dal'she, v tochnosti napominaya kartinku, vyrezannuyu iz kartona. Tut mister
Tompkins oshchutil neobychnyj priliv gordosti, ibo emu bylo sovershenno yasno, chto
proishodilo s velosipedistom - eto bylo ne chto inoe, kak sokrashchenie
dvizhushchihsya tel v napravlenii dvizheniya, o kotorom tol'ko chto rasskazyval
lektor.
- Dolzhno byt', estestvennaya predel'naya skorost' zdes' pomen'she, chem u
nas, - podumal mister Tompkins, - poetomu policejskij na uglu vyglyadit takim
lenivym: emu ne nuzhno sledit', chtoby nikto ne narushal ogranichenij na
skorost'.
V tot den' vse banki byli zakryty - vyhodnoj, i mister Tompkins,
skromnyj sluzhashchij solidnogo gorodskogo banka, vstal pozzhe obychnogo i ne
spesha pozavtrakal. Pora bylo pozabotit'sya o dosuge, i mister Tompkins reshil,
chto bylo by neploho shodit' na dnevnoj seans v kino. Razvernuv utrennyuyu
gazetu na toj polose, gde publikovalas' informaciya o razvlecheniyah, on
uglubilsya v izuchenie repertuara kinoteatrov. Ni odin iz reklamiruemyh
fil'mov ne pokazalsya misteru Tompkinsu dostatochno privlekatel'nym. On
terpet' ne mog vsyu etu gollivudskuyu drebeden' s neskonchaemymi lyubovnymi
istoriyami, razygryvaemymi populyarnymi kinozvezdami. Vot esli by nashelsya hotya
by odin fil'm s syuzhetom, zaimstvovannym iz real'noj zhizni, byt' mozhet, s
primes'yu chego-nibud' neobychnogo ili dazhe fantasticheskogo! No takih fil'mov -
uvy! - ne bylo. Neozhidanno vnimanie mistera Tompkinsa privleklo nebol'shoe
ob座avlenie v samom uglu gazetnoj polosy. Mestnyj universitet dovodil do
svedeniya vseh zhelayushchih, chto v ego pomeshchenii budet prochitan cikl lekcij po
problemam sovremennoj fiziki. Blizhajshaya lekciya sostoitsya segodnya vecherom i
budet posvyashchena teorii otnositel'nosti |jnshtejna. Vot eto stoyashchee delo!
Misteru Tompkinsu chasten'ko prihodilos' slyshat', chto vo vsem mire edva li
dyuzhina lyudej po-nastoyashchemu ponimayut teoriyu |jnshtejna! A chto esli on, mister
Tomggkins, stanet trinadcatym? YAsnoe delo: on nepremenno otpravitsya na
lekciyu. |to kak raz to, chto emu nuzhno! Kogda mister Tompkins voshel v bol'shuyu
universitetskuyu auditoriyu, lekciya uzhe nachalas'. Vse pomeshchenie bylo bitkom
nabito studentami (v osnovnom eto byli molodye lyudi), s nepoddel'nym
interesom vnimavshimi vysokomu sedoborodomu cheloveku u doski, kotoryj pytalsya
ob座asnit' auditorii osnovnye idei teorii otnositel'nosti. Iz slov lektora
mister Tompkins ponyal tol'ko, chto osnovnoj punkt teorii |jnshtejna -
sushchestvovanie maksimal'noj skorosti - skorosti sveta, kotoruyu ne mozhet
prevzojti ni odno dvizhushcheesya material'noe telo, i chto eto obstoyatel'stvo
privodit k ves'ma strannym i neobychnym sledstviyam. Pravda, professor
zametil, chto, poskol'ku skorost' sveta sostavlyaet 300000 kilometrov v
sekundu, relyativistskie (t.e. svyazannee s teoriej otnositel'nosti) effekty
edva li mogut nablyudat'sya v yavleniyah povsednevnoj zhizni. CHto zhe kasaetsya
prirody etih neobychnyh effektov, to ponyat' ee bylo nesravnenno trudnee, i
misteru Tompkinsu pokazalos', chto vse, o chem govorit lektor, protivorechilo
zdravomu smyslu. On popytalsya myslenno predstavit' sebe sokrashchenie
izmeritel'nyh sterzhnej i strannoe povedenie chasov - effekty, kotoryh
sledovalo by ozhidat' pri dvizhenii so skorost'yu, blizkoj k skorosti sveta, no
tut golova ego medlenno sklonilas' na plecho.
Kogda mister Tompkins snova otkryl glaza, on obnaruzhil, chto sidit ne na
skam'e v universitetskoj auditorii, a na skamejkah, ustanovlennyh gorodskimi
vlastyami dlya udobstva passazhirov, ozhidayushchih avtobus. Krugom prostiralsya
krasivyj starinnyj gorodok so srednevekovymi zdaniyami kolledzhej,
vystroivshimisya vdol' ulicy. Mister Tompkins zapodozril bylo, chto vidit vse
eto vo sne, no k ego udivleniyu nichego neobychnogo vokrug ne proishodilo, dazhe
polismen, stoyavshij na protivopolozhnom uglu, vyglyadel tak, kak obychno
vyglyadyat polismeny. Strelki bol'shih chasov na bashne v konce ulicy pokazyvali
pyat' chasov, i ulicy byli pochti pustynnymi. Odinokij velosipedist pokazalsya
vdali i stal medlenno priblizhat'sya. Kogda on pod容hal poblizhe, mister
Tompkins vytarashchil glaza ot izumleniya: i velosiped, i vossedavshij na nem
molodoj chelovek byli neveroyatno sokrashcheny v napravlenii dvizheniya, kak budto
ih rassmatrivali cherez cilindricheskuyu linzu. CHasy na bashne probili pyat', i
velosipedist, po-vidimomu, kuda-to speshivshij, prinaleg na pedali. Mister
Tompkins ne zametil, chtoby skorost' ot etogo pribavilas', no usiliya
velosipedista ne proshli bessledno: on sokratilsya eshche sil'nee i otpravilsya
dal'she, v tochnosti napominaya kartinku, vyrezannuyu iz kartona. Tut mister
Tompkins oshchutil neobychnyj priliv gordosti, ibo emu bylo sovershenno yasno, chto
proishodilo s velosipedistom - eto bylo ne chto inoe, kak sokrashchenie
dvizhushchihsya tel v napravlenii dvizheniya, o kotorom tol'ko chto rasskazyval
lektor.
- Dolzhno byt', estestvennaya predel'naya skorost' zdes' pomen'she, chem u
nas, - podumal mister Tompkins, - poetomu policejskij na uglu vyglyadit takim
lenivym: emu ne nuzhno sledit', chtoby nikto ne narushal ogranichenij na
skorost'.
 Dejstvitel'no, poyavivsheesya na ulice taksi proizvodilo grohot i skrezhet,
sposobnye razbudit' i mertvogo, no prodvigalos' ne namnogo bystree, chem
velosipedist, i, esli skazat' chestno, polzlo ele-ele. Mister Tompkins reshil
dognat' velosipedista, kotoryj na vid byl simpatichnym malym, i rassprosit'
ego obo vsem. Ubedivshis', chto polismen otvernulsya i smotrit v druguyu
storonu, mister Tompkins vospol'zovalsya ch'im-to velosipedom, stoyavshim u kraya
trotuara, i pomchalsya po ulice. On ozhidal, chto srazu zhe sokratitsya v
napravlenii dvizheniya i dazhe byl ochen' rad etomu, tak kak nachavshaya
raspolzat'sya za poslednee vremya figura prichinyala emu nekotorye nepriyatnosti.
No k velichajshemu udivleniyu mistera Tompkinsa ni s nim samim, ni s
velosipedom nichego ne proizoshlo. Sokratilis' ulicy, vitriny lavok i
magazinov prevratilis' v uzkie shcheli, a polismen na uglu stal samym toshchim
chelovekom, kotorogo prihodilos' kogda-nibud' videt' misteru Tompkinsu.
- Klyanus' YUpiterom, - radostno voskliknul mister Tompkins, - ya,
kazhetsya, ponyal, v chem delo! Vot gde poyavlyaetsya slovechko "otnositel'nost'".
Vse, chto dvizhetsya otnositel'no menya, kazhetsya mne sokrashchennym, kto by ni
krutil pedali!
Dejstvitel'no, poyavivsheesya na ulice taksi proizvodilo grohot i skrezhet,
sposobnye razbudit' i mertvogo, no prodvigalos' ne namnogo bystree, chem
velosipedist, i, esli skazat' chestno, polzlo ele-ele. Mister Tompkins reshil
dognat' velosipedista, kotoryj na vid byl simpatichnym malym, i rassprosit'
ego obo vsem. Ubedivshis', chto polismen otvernulsya i smotrit v druguyu
storonu, mister Tompkins vospol'zovalsya ch'im-to velosipedom, stoyavshim u kraya
trotuara, i pomchalsya po ulice. On ozhidal, chto srazu zhe sokratitsya v
napravlenii dvizheniya i dazhe byl ochen' rad etomu, tak kak nachavshaya
raspolzat'sya za poslednee vremya figura prichinyala emu nekotorye nepriyatnosti.
No k velichajshemu udivleniyu mistera Tompkinsa ni s nim samim, ni s
velosipedom nichego ne proizoshlo. Sokratilis' ulicy, vitriny lavok i
magazinov prevratilis' v uzkie shcheli, a polismen na uglu stal samym toshchim
chelovekom, kotorogo prihodilos' kogda-nibud' videt' misteru Tompkinsu.
- Klyanus' YUpiterom, - radostno voskliknul mister Tompkins, - ya,
kazhetsya, ponyal, v chem delo! Vot gde poyavlyaetsya slovechko "otnositel'nost'".
Vse, chto dvizhetsya otnositel'no menya, kazhetsya mne sokrashchennym, kto by ni
krutil pedali!
 Mister Tompkins byl neplohim velosipedistom i izo vseh sil staralsya
dognat' molodogo cheloveka. Odnako on obnaruzhil, chto razvit' prilichnuyu
skorost' na ugnannom im velosipede sovsem nelegko. Hotya mister Tompkins
krutil pedali chto bylo sil, skorost' ot etogo pribavlyalas' edva zametno.
Nogi u nego uzhe nachalo svodit' ot napryazheniya, a emu nikak ne udavalos'
minovat' fonarnyj stolb na uglu bystree, chem kogda on tol'ko pustilsya v
put'. Kazalos', vse ego usiliya ehat' bystree tshchetny. Teper' on otlichno
ponyal, pochemu velosipedist i vstretivsheesya emu tol'ko chto taksi polzli s
takoj cherepash'ej skorost'yu. Vspomnilis' emu i slova professora o tom, chto ni
odno dvizhushcheesya telo ne mozhet prevzojti predel'nuyu skorost' - skorost'
sveta. Pravda, mister Tompkins zametil, chto gorodskie kvartaly sokrashchalis'
vse bol'she i do ehavshego vperedi velosipedista teper' kazalos' ne tak
daleko. U vtorogo povorota misteru Tompkinsu udalos' dognat' velosipedista i
v tot samyj moment, kogda oni porovnyalis', ehali ryadom, mister Tompkins,
vzglyanuv na togo, k svoemu udivleniyu uvidel, chto pered nim obychnyj molodoj
chelovek sportivnogo vida.
- Dolzhno byt', eto ot togo, chto my ne dvizhemsya drug otnositel'no druga,
- podumal mister Tompkins i obratilsya k molodomu cheloveku:
- Proshu proshcheniya, ser! - skazal on. - Ne nahodite li vy, chto zhizn' v
gorode so stol' nizkoj predel'noj skorost'yu sopryazhena s nekotorymi
neudobstvami?
- O kakoj predel'noj skorosti vy govorite? - s nedoumeniem sprosil
molodoj chelovek. - U nas v gorode net nikakih ogranichenij na skorost'. YA
mogu ehat' gde ugodno i kuda ugodno s lyuboj skorost'yu, kakaya mne tol'ko
zablagorassuditsya ili po krajnej mere s kakoj mog by dvigat'sya, bud' u menya
motocikl, a ne eta dopotopnaya razvalina, iz kotoroj, kak ni starajsya,
prilichnoj skorosti ne vyzhmesh'!
- No kogda vy nedavno proezzhali mimo menya, - prodolzhal mister Tompkins,
- to tashchilis' ele-ele. YA obratil na eto vnimanie.
- V samom dele? - molodoj chelovek byl yavno zadet podobnym zamechaniem. -
V takom sluchae vy, veroyatno, zametili, chto vpervye obratilis' ko mne, kogda
my byli otsyuda v pyati kvartalah. Dlya vas eto nedostatochno bystro?
- No s teh por ulicy znachitel'no sokratilis', - prodolzhal nastaivat'
mister Tompkins.
- A kakaya raznica, dvizhemsya li my bystree ili ulica stanovitsya koroche?
Mne nuzhno proehat' desyat' kvartalov, chtoby popast' na pochtu, i esli ya budu
prilezhnee krutit' pedali, to kvartaly stanut koroche i ya bystree popadu na
pochtu. Vprochem, vot my i doehali.
S etimi slovami molodoj chelovek soskochil s velosipeda.
Mister Tompkins vzglyanul na chasy na zdanii pochty: oni pokazyvali
polshestogo.
- Vot vidite, - zametil on torzhestvuyushche, - chtoby proehat' kakih-nibud'
desyat' kvartalov, vam ponadobilos' polchasa. Ved' kogda ya vpervye uvidel vas,
bylo rovno pyat'!
- I vy pochuvstvovali, chto proshlo polchasa? - sprosil ego sobesednik.
Misteru Tompkinsu prishlos' priznat', chto po ego oshchushcheniyam proshlo vsego
neskol'ko minut. Krome togo, vzglyanuv na svoi ruchnye chasy, on uvidel, chto
oni pokazyvayut tol'ko pyat' minut shestogo.
- O! - tol'ko i smog vymolvit' on. - CHasy na zdanii pochty speshat?
- Razumeetsya, speshat ili - vashi chasy otstayut, potomu chto vy dvigaetes'
slishkom bystro. Da chto s vami v samom dele? Vy chto, s Luny svalilis'? - i
molodoj chelovek voshel v zdanie pochty.
Posle etogo razgovora mister Tompkins pozhalel, chto ryadom net starogo
professora, kotoryj by ob座asnil emu eti strannye sobytiya. Molodoj chelovek,
po-vidimomu, byl mestnym zhitelem i privyk k takomu sostoyaniyu veshchej prezhde,
chem nauchilsya hodit'. Misteru Tompkinsu ne ostavalos' nichego drugogo, kak
samomu prinyat'sya za issledovanie okruzhavshego ego strannogo mira. On postavil
svoi chasy po chasam na zdanii pochty i, chtoby ubedit'sya v tom, chto ego chasy
idut pravil'no, vyzhdal minut desyat'. Ego ruchnye chasy ne otstavali. Prodolzhiv
svoe puteshestvie po ulice, mister Tompkins, nakonec, dobralsya do vokzala i
reshil snova sverit' svoi chasy. K ego udivleniyu, chasy snova nemnogo otstali.
- Dolzhno byt', eto takzhe kakoj-to relyativistskij effekt, - reshil mister
Tompkins i podumal, chto bylo by nedurno rassprosit' ob etom kogo-nibud'
poumnee yunogo velosipedista.
Udobnyj sluchaj predstavilsya ochen' skoro. Dzhentl'men, na vid let soroka,
soshel s poezda i napravilsya k vyhodu. Ego vstrechala ledi ves'ma preklonnogo
vozrasta, kotoraya, k udivleniyu mistera Tompkinsa, nazyvala ego ne inache, kak
"moj dorogoj dedushka". Dlya mistera Tompkinsa eto bylo uzhe chereschur. Pod
predlogom pomoch' podnesti veshchi on vmeshalsya v razgovor.
- Proshu izvinit' menya za to, chto vmeshivayus' v vashi semejnye dela, -
nachal on, - no dejstvitel'no li vy prihodites' dedushkoj etoj miloj pozhiloj
ledi? Vidite li, ya v etih mestah chelovek novyj i ne znayu mestnyh obychaev, no
mne nikogda ne dovodilos'...
- Ponimayu vashe zatrudnenie, - ulybnulsya v usy dzhentl'men. - Dolzhno
byt', vy prinimaete menya za Vechnogo ZHida ili kogo-nibud' v tom zhe duhe. No v
dejstvitel'nosti vse obstoit ochen' prosto. Moya professiya vynuzhdaet menya
mnogo ezdit', i bol'shuyu chast' svoej zhizni ya provozhu v poezde i poetomu,
estestvenno, stareyu gorazdo medlennee, chem moi rodstvenniki, prozhivayushchie v
gorode. YA tak rad, chto sumel vernut'sya vovremya i zastal eshche v zhivyh moyu
lyubimuyu vnuchku! No proshu menya izvinit', mne nuzhno provodit' ee do taksi, - i
dzhentl'men pospeshil proch', ostaviv mistera Tompkinsa odin na odin s ego
problemami. Para buterbrodov iz vokzal'nogo bufeta neskol'ko podkrepili ego
umstvennye sposobnosti, i on zashel v svoih rassuzhdeniyah tak daleko, chto
zayavil, budto emu udalos' obnaruzhit' protivorechie v znamenitom principe
otnositel'nosti.
- Esli by vse bylo otnositel'no, - razmyshlyal on, othlebyvaya kofe, - to
puteshestvennik kazalsya by svoim osedlym rodstvennikam ochen' starym, a oni v
svoyu ochered' kazalis' by ochen' starymi emu, hotya v dejstvitel'nosti obe
storony byli by dostatochno molodymi, No to, chto ya utverzhdayu teper', kazhetsya
sovershennejshej chepuhoj: ni u kogo ne mozhet byt' "otnositel'no sedyh volos!"
Tut mister Tompkins reshil predprinyat' poslednyuyu popytku razobrat'sya v
tom, kak obstoit delo v dejstvitel'nosti, i obratilsya k cheloveku v
zheleznodorozhnoj forme, odinoko sidevshemu v bufete.
- Ne budete li vy tak lyubezny, - nachal on, - ne budete li vy tak dobry
skazat', kto vinovat v tom, chto passazhiry v poezde stareyut gorazdo medlennee
teh lyudej, kotorye ostayutsya doma?
- Vo vsem vinovat ya, ser, - ochen' spokojno otvetil neznakomec.
- O! - voskliknul mister Tompkins. - Tak vam udalos' razreshit' problemu
filosofskogo kamnya, nad kotoroj v starinu stol'ko bilis' alhimiki. Dolzhno
byt', vy ochen' znamenity v medicinskom mire. Vy vozglavlyaete gde-nibud'
kafedru?
- Net, - otvetil neznakomec, neobychajno udivlennyj tem, chto skazal
mister Tompkins. - YA tormoznoj konduktor i v moi obyazannosti vhodit vovremya
tormozit'.
- Tormoznoj konduktor! - voskliknul mister Tompkins, chuvstvuya, chto
pochva uhodit u nego iz-pod nog. - Tak vy dumaete, chto vy ... Vy
dejstvitel'no tol'ko nazhimaete na tormoz, kogda poezd podhodit k stancii?
- Sovershenno verno! Imenno eto ya i delayu, i vsyakij raz, kogda poezd
zamedlyaet svoj hod, passazhiry stanovyatsya chut' starshe drugih lyudej.
- Razumeetsya, - skromno dobavil konduktor, - mashinist, kotoryj
razgonyaet poezd, takzhe vypolnyaet svoyu chast' raboty.
- A kakoe otnoshenie tormozhenie i razgon poezda imeyut k tomu, chto odni
ostayutsya molodymi, a drugie stareyut? - v izumlenii sprosil mister Tomkins.
- Kakaya tut svyaz', mne dopodlinno neizvestno, - skazal konduktor, -
znayu tol'ko, chto ona est'. Odnazhdy sredi passazhirov mne vstretilsya professor
iz universiteta, i ya sprosil u nego, kak eto poluchaetsya. On pustilsya v
dlinnye i malovrazumitel'nye ob座asneniya, a pod konec upomyanul o kakom-to
"gravitacionnom krasnom smeshchenii (kazhetsya, on vyrazilsya imenno tak) na
Solnce". Prihodilos' li vam slyshat' o chem-nibud' podobnom? CHto eto za zver'
takoj - krasnoe smeshchenie?
- Ne-et, - zadumchivo protyanul mister Tompkins, i konduktor poshel svoej
dorogoj, kachaya golovoj.
Vdrug ch'ya-to tyazhelaya ruka opustilas' na plecho mistera Tompkinsa, i,
ochnuvshis', on obnaruzhil, chto sidit ne v vokzal'nom bufete, a na skam'e v toj
samoj universitetskoj auditorii, gde on slushal lekciyu professora. Svet uzhe
byl potushen, i auditoriya opustela. Razbudivshij ego universitetskij sluzhitel'
myagko zametil:
- My zakryvaemsya, ser! Esli hotite spat', stupajte luchshe k sebe domoj.
Mister Tompkins vstal i napravilsya k vyhodu.
lekciya professora o teorii otnositel'nosti, na kotoroj zasnul mister
Tompkins
Ledi i dzhentl'meny!
CHelovecheskij razum sformiroval opredelennye predstavleniya o
prostranstve i vremeni kak o vmestilishche ili arene, na kotoroj proishodyat
razlichnye sobytiya. |ti predstavleniya bez osobyh izmenenij peredavalis' iz
pokoleniya v pokolenie, a so vremeni zarozhdeniya tochnyh nauk byli vklyucheny v
samye osnovy matematicheskogo opisaniya okruzhayushchego nas mira. Velikij N'yuton,
po-vidimomu, pervym dal chetkuyu formulirovku klassicheskih ponyatij
prostranstva i vremeni, napisav v svoih "Matematicheskih nachalah":
"_Absolyutnoe prostranstvo_ po samoj svoej sushchnosti, bezotnositel'no k
chemu by to ni bylo vneshnemu, ostaetsya vsegda odinakovym i nepodvizhnym" i
"_Absolyutnoe, istinnoe matematicheskoe vremya_ samo po sebe i po samoj svoej
sushchnosti, bez vsyakogo otnosheniya k chemu-libo vneshnemu, protekaet ravnomerno i
inache nazyvaetsya dlitel'nost'yu" {N'yuton I. Matematicheskie nachala natural'noj
filosofii. - Per. s latinskogo i kommentarii A.N. Krylova. Predislovie
L.S.Polaka. - M.: Nauka, 1989. - S. 30. (Prim. per.)}.
- Ubezhdenie v absolyutnoj pravil'nosti etih klassicheskih predstavlenij o
prostranstve i vremeni bylo stol' sil'nym, chto filosofy chasto schitali ih
apriornymi i ni odnomu uchenomu-estestvoispytatelyu dazhe v golovu ne prihodilo
usomnit'sya v nih. Odnako v nachale XX veka stalo yasno, chto ryad rezul'tatov,
poluchennyh s pomoshch'yu chuvstvitel'nyh i tonkih metodov eksperimental'noj
fiziki, privodyat k protivorechiyam, esli ih interpretirovat' v ramkah
klassicheskih predstavlenij o prostranstve i vremeni. |to obstoyatel'stvo
privelo odnogo iz velichajshih sovremennyh fizikov Al'berta |jnshtejna k
revolyucionnoj idee: ne sushchestvuet nikakih prichin, krome tradicii, po kotorym
klassicheskie predstavleniya o prostranstve i vremeni sledovalo by schitat'
absolyutno pravil'nymi; v eti ponyatiya mozhno i dolzhno vnosit' izmeneniya, chtoby
oni sootvetstvovali nashemu novomu, bolee tochnomu opytu. Dejstvitel'no,
klassicheskie ponyatiya prostranstva i vremeni byli sformulirovany na osnove
chelovecheskogo opyta, pocherpnutogo iz povsednevnoj zhizni. Nuzhno li
udivlyat'sya, chto tonkie i tochnye sovremennye metody nablyudeniya, osnovannye na
ispol'zovanii vysokorazvitoj eksperimental'noj tehniki, ukazyvayut na to, chto
starye ponyatiya prostranstva i vremeni slishkom gruby, netochny i mogli
ispol'zovat'sya v povsednevnoj zhizni i na bolee rannih stadiyah razvitiya
fiziki tol'ko potomu, chto ih otkloneniya ot pravil'nyh ponyatij dostatochno
maly. Ne sleduet udivlyat'sya i tomu, chto rasshirenie oblasti issledovanij
sovremennoj nauki rano ili pozdno dolzhno bylo privesti nas v takie oblasti,
gde eti otkloneniya ves'ma veliki i klassicheskie ponyatiya voobshche ne primenimy.
Samym vazhnym eksperimental'nym rezul'tatom, privedshim k korennomu
peresmotru nashih klassicheskih predstavlenij, stalo otkrytie togo fakta, chto
skorost' sveta v pustote predstavlyaet soboj verhnij predel vseh vozmozhnyh
fizicheskih skorostej. Takoj vazhnyj i neozhidannyj vyvod byl sdelan glavnym
obrazom na osnovanii eksperimentov amerikanskogo fizika Majkel'sona, kotoryj
v konce proshlogo veka predprinyal popytku nablyudat' vliyanie dvizheniya Zemli na
skorost' rasprostraneniya sveta i k svoemu velikomu udivleniyu i k udivleniyu
vsego nauchnogo mira obnaruzhil, chto nikakih effektov, svidetel'stvuyushchih o
vliyanii skorosti dvizheniya Zemli na skorost' sveta, ne sushchestvuet i chto
skorost' sveta v pustote okazyvaetsya vsegda odnoj i toj zhe, nezavisimo ot
sistemy, v kotoroj proizvoditsya izmerenie, ili ot dvizheniya istochnika,
ispuskayushchego svet. Net neobhodimosti ob座asnyat', pochemu takoj rezul'tat
ves'ma neobychen i protivorechit nashim fundamental'nym predstavleniyam o
dvizhenii. Dejstvitel'no, esli kakoj-to ob容kt bystro dvizhetsya v
prostranstve, a vy dvizhetes' navstrechu emu, to dvizhushchijsya ob容kt stolknetsya
s vami s bol'shej otnositel'noj skorost'yu, ravnoj summe skorostej ob容kta i
nablyudatelya. S drugoj storony, esli vy udalyaetes' ot ob容kta, to on, dognav
vas szadi, stolknetsya s vami s men'shej otnositel'noj skorost'yu, ravnoj
raznosti skorostej.
Naprimer, esli vy dvizhetes', skazhem, edete v avtomashine, navstrechu
rasprostranyayushchemusya v vozduhe zvuku, to izmerennaya iz mashiny skorost' zvuka
budet bol'she na velichinu, ravnuyu skorosti, razvivaemoj vashej mashinoj, ili,
sootvetstvenno, men'she, esli zvuk dogonyaet vas. My nazyvaem eto _teoremoj
slozheniya skorostej_. Vsegda schitalos', chto eta teorema samoochevidna.
Odnako, kak pokazali samye tshchatel'nye eksperimenty, v sluchae sveta
teorema slozheniya skorostej narushaetsya: skorost' sveta v pustote vsegda
ostaetsya odnoj i toj zhe i ravna 300000 km/s (skorost' sveta prinyato
oboznachat' strochnoj latinskoj bukvoj s) nezavisimo ot togo, kak bystro
dvizhetsya nablyudatel'.
- Vse eto horosho, - skazhete vy, - no razve nel'zya postroit'
sverhsvetovuyu skorost', skladyvaya neskol'ko men'shih, fizicheski dostizhimyh
skorostej?
Mozhem zhe my predstavit' sebe dvizhushchijsya ochen' bystro (naprimer, so
skorost'yu, ravnoj 3/4 skorosti sveta) poezd i brodyagu, begushchego po krysham
vagonov takzhe so skorost'yu, ravnoj 3/4 skorosti sveta.
Po teoreme slozheniya skorostej, obshchaya skorost' brodyagi byla by ravna
polutora skorostyam sveta, i brodyaga mog by obognat' svet, ispuskaemyj
signal'nym fonarem. Odnako istina sostoit v tom, chto, poskol'ku postoyanstvo
skorosti sveta est' eksperimental'nyj fakt, rezul'tiruyushchaya skorost' v nashem
sluchae dolzhna byt' men'she, chem my ozhidaem, - ona ne mozhet prevoshodit'
kriticheskogo znacheniya s. Takim obrazom, my prihodim k vyvodu o tom, chto i
pri men'shih skorostyah klassicheskaya teorema slozheniya skorostej dolzhna byt'
neverna.
Matematicheskij analiz problemy, v kotoryj ya ne hochu zdes' vdavat'sya,
privodit k ochen' prostoj novoj formule dlya vychisleniya rezul'tiruyushchej
skorosti dvuh skladyvaemyh dvizhenij.
Esli u1 i u2 - dve podlezhashchie slozheniyu skorosti, to rezul'tiruyushchaya
skorost' okazyvaetsya ravnoj
Mister Tompkins byl neplohim velosipedistom i izo vseh sil staralsya
dognat' molodogo cheloveka. Odnako on obnaruzhil, chto razvit' prilichnuyu
skorost' na ugnannom im velosipede sovsem nelegko. Hotya mister Tompkins
krutil pedali chto bylo sil, skorost' ot etogo pribavlyalas' edva zametno.
Nogi u nego uzhe nachalo svodit' ot napryazheniya, a emu nikak ne udavalos'
minovat' fonarnyj stolb na uglu bystree, chem kogda on tol'ko pustilsya v
put'. Kazalos', vse ego usiliya ehat' bystree tshchetny. Teper' on otlichno
ponyal, pochemu velosipedist i vstretivsheesya emu tol'ko chto taksi polzli s
takoj cherepash'ej skorost'yu. Vspomnilis' emu i slova professora o tom, chto ni
odno dvizhushcheesya telo ne mozhet prevzojti predel'nuyu skorost' - skorost'
sveta. Pravda, mister Tompkins zametil, chto gorodskie kvartaly sokrashchalis'
vse bol'she i do ehavshego vperedi velosipedista teper' kazalos' ne tak
daleko. U vtorogo povorota misteru Tompkinsu udalos' dognat' velosipedista i
v tot samyj moment, kogda oni porovnyalis', ehali ryadom, mister Tompkins,
vzglyanuv na togo, k svoemu udivleniyu uvidel, chto pered nim obychnyj molodoj
chelovek sportivnogo vida.
- Dolzhno byt', eto ot togo, chto my ne dvizhemsya drug otnositel'no druga,
- podumal mister Tompkins i obratilsya k molodomu cheloveku:
- Proshu proshcheniya, ser! - skazal on. - Ne nahodite li vy, chto zhizn' v
gorode so stol' nizkoj predel'noj skorost'yu sopryazhena s nekotorymi
neudobstvami?
- O kakoj predel'noj skorosti vy govorite? - s nedoumeniem sprosil
molodoj chelovek. - U nas v gorode net nikakih ogranichenij na skorost'. YA
mogu ehat' gde ugodno i kuda ugodno s lyuboj skorost'yu, kakaya mne tol'ko
zablagorassuditsya ili po krajnej mere s kakoj mog by dvigat'sya, bud' u menya
motocikl, a ne eta dopotopnaya razvalina, iz kotoroj, kak ni starajsya,
prilichnoj skorosti ne vyzhmesh'!
- No kogda vy nedavno proezzhali mimo menya, - prodolzhal mister Tompkins,
- to tashchilis' ele-ele. YA obratil na eto vnimanie.
- V samom dele? - molodoj chelovek byl yavno zadet podobnym zamechaniem. -
V takom sluchae vy, veroyatno, zametili, chto vpervye obratilis' ko mne, kogda
my byli otsyuda v pyati kvartalah. Dlya vas eto nedostatochno bystro?
- No s teh por ulicy znachitel'no sokratilis', - prodolzhal nastaivat'
mister Tompkins.
- A kakaya raznica, dvizhemsya li my bystree ili ulica stanovitsya koroche?
Mne nuzhno proehat' desyat' kvartalov, chtoby popast' na pochtu, i esli ya budu
prilezhnee krutit' pedali, to kvartaly stanut koroche i ya bystree popadu na
pochtu. Vprochem, vot my i doehali.
S etimi slovami molodoj chelovek soskochil s velosipeda.
Mister Tompkins vzglyanul na chasy na zdanii pochty: oni pokazyvali
polshestogo.
- Vot vidite, - zametil on torzhestvuyushche, - chtoby proehat' kakih-nibud'
desyat' kvartalov, vam ponadobilos' polchasa. Ved' kogda ya vpervye uvidel vas,
bylo rovno pyat'!
- I vy pochuvstvovali, chto proshlo polchasa? - sprosil ego sobesednik.
Misteru Tompkinsu prishlos' priznat', chto po ego oshchushcheniyam proshlo vsego
neskol'ko minut. Krome togo, vzglyanuv na svoi ruchnye chasy, on uvidel, chto
oni pokazyvayut tol'ko pyat' minut shestogo.
- O! - tol'ko i smog vymolvit' on. - CHasy na zdanii pochty speshat?
- Razumeetsya, speshat ili - vashi chasy otstayut, potomu chto vy dvigaetes'
slishkom bystro. Da chto s vami v samom dele? Vy chto, s Luny svalilis'? - i
molodoj chelovek voshel v zdanie pochty.
Posle etogo razgovora mister Tompkins pozhalel, chto ryadom net starogo
professora, kotoryj by ob座asnil emu eti strannye sobytiya. Molodoj chelovek,
po-vidimomu, byl mestnym zhitelem i privyk k takomu sostoyaniyu veshchej prezhde,
chem nauchilsya hodit'. Misteru Tompkinsu ne ostavalos' nichego drugogo, kak
samomu prinyat'sya za issledovanie okruzhavshego ego strannogo mira. On postavil
svoi chasy po chasam na zdanii pochty i, chtoby ubedit'sya v tom, chto ego chasy
idut pravil'no, vyzhdal minut desyat'. Ego ruchnye chasy ne otstavali. Prodolzhiv
svoe puteshestvie po ulice, mister Tompkins, nakonec, dobralsya do vokzala i
reshil snova sverit' svoi chasy. K ego udivleniyu, chasy snova nemnogo otstali.
- Dolzhno byt', eto takzhe kakoj-to relyativistskij effekt, - reshil mister
Tompkins i podumal, chto bylo by nedurno rassprosit' ob etom kogo-nibud'
poumnee yunogo velosipedista.
Udobnyj sluchaj predstavilsya ochen' skoro. Dzhentl'men, na vid let soroka,
soshel s poezda i napravilsya k vyhodu. Ego vstrechala ledi ves'ma preklonnogo
vozrasta, kotoraya, k udivleniyu mistera Tompkinsa, nazyvala ego ne inache, kak
"moj dorogoj dedushka". Dlya mistera Tompkinsa eto bylo uzhe chereschur. Pod
predlogom pomoch' podnesti veshchi on vmeshalsya v razgovor.
- Proshu izvinit' menya za to, chto vmeshivayus' v vashi semejnye dela, -
nachal on, - no dejstvitel'no li vy prihodites' dedushkoj etoj miloj pozhiloj
ledi? Vidite li, ya v etih mestah chelovek novyj i ne znayu mestnyh obychaev, no
mne nikogda ne dovodilos'...
- Ponimayu vashe zatrudnenie, - ulybnulsya v usy dzhentl'men. - Dolzhno
byt', vy prinimaete menya za Vechnogo ZHida ili kogo-nibud' v tom zhe duhe. No v
dejstvitel'nosti vse obstoit ochen' prosto. Moya professiya vynuzhdaet menya
mnogo ezdit', i bol'shuyu chast' svoej zhizni ya provozhu v poezde i poetomu,
estestvenno, stareyu gorazdo medlennee, chem moi rodstvenniki, prozhivayushchie v
gorode. YA tak rad, chto sumel vernut'sya vovremya i zastal eshche v zhivyh moyu
lyubimuyu vnuchku! No proshu menya izvinit', mne nuzhno provodit' ee do taksi, - i
dzhentl'men pospeshil proch', ostaviv mistera Tompkinsa odin na odin s ego
problemami. Para buterbrodov iz vokzal'nogo bufeta neskol'ko podkrepili ego
umstvennye sposobnosti, i on zashel v svoih rassuzhdeniyah tak daleko, chto
zayavil, budto emu udalos' obnaruzhit' protivorechie v znamenitom principe
otnositel'nosti.
- Esli by vse bylo otnositel'no, - razmyshlyal on, othlebyvaya kofe, - to
puteshestvennik kazalsya by svoim osedlym rodstvennikam ochen' starym, a oni v
svoyu ochered' kazalis' by ochen' starymi emu, hotya v dejstvitel'nosti obe
storony byli by dostatochno molodymi, No to, chto ya utverzhdayu teper', kazhetsya
sovershennejshej chepuhoj: ni u kogo ne mozhet byt' "otnositel'no sedyh volos!"
Tut mister Tompkins reshil predprinyat' poslednyuyu popytku razobrat'sya v
tom, kak obstoit delo v dejstvitel'nosti, i obratilsya k cheloveku v
zheleznodorozhnoj forme, odinoko sidevshemu v bufete.
- Ne budete li vy tak lyubezny, - nachal on, - ne budete li vy tak dobry
skazat', kto vinovat v tom, chto passazhiry v poezde stareyut gorazdo medlennee
teh lyudej, kotorye ostayutsya doma?
- Vo vsem vinovat ya, ser, - ochen' spokojno otvetil neznakomec.
- O! - voskliknul mister Tompkins. - Tak vam udalos' razreshit' problemu
filosofskogo kamnya, nad kotoroj v starinu stol'ko bilis' alhimiki. Dolzhno
byt', vy ochen' znamenity v medicinskom mire. Vy vozglavlyaete gde-nibud'
kafedru?
- Net, - otvetil neznakomec, neobychajno udivlennyj tem, chto skazal
mister Tompkins. - YA tormoznoj konduktor i v moi obyazannosti vhodit vovremya
tormozit'.
- Tormoznoj konduktor! - voskliknul mister Tompkins, chuvstvuya, chto
pochva uhodit u nego iz-pod nog. - Tak vy dumaete, chto vy ... Vy
dejstvitel'no tol'ko nazhimaete na tormoz, kogda poezd podhodit k stancii?
- Sovershenno verno! Imenno eto ya i delayu, i vsyakij raz, kogda poezd
zamedlyaet svoj hod, passazhiry stanovyatsya chut' starshe drugih lyudej.
- Razumeetsya, - skromno dobavil konduktor, - mashinist, kotoryj
razgonyaet poezd, takzhe vypolnyaet svoyu chast' raboty.
- A kakoe otnoshenie tormozhenie i razgon poezda imeyut k tomu, chto odni
ostayutsya molodymi, a drugie stareyut? - v izumlenii sprosil mister Tomkins.
- Kakaya tut svyaz', mne dopodlinno neizvestno, - skazal konduktor, -
znayu tol'ko, chto ona est'. Odnazhdy sredi passazhirov mne vstretilsya professor
iz universiteta, i ya sprosil u nego, kak eto poluchaetsya. On pustilsya v
dlinnye i malovrazumitel'nye ob座asneniya, a pod konec upomyanul o kakom-to
"gravitacionnom krasnom smeshchenii (kazhetsya, on vyrazilsya imenno tak) na
Solnce". Prihodilos' li vam slyshat' o chem-nibud' podobnom? CHto eto za zver'
takoj - krasnoe smeshchenie?
- Ne-et, - zadumchivo protyanul mister Tompkins, i konduktor poshel svoej
dorogoj, kachaya golovoj.
Vdrug ch'ya-to tyazhelaya ruka opustilas' na plecho mistera Tompkinsa, i,
ochnuvshis', on obnaruzhil, chto sidit ne v vokzal'nom bufete, a na skam'e v toj
samoj universitetskoj auditorii, gde on slushal lekciyu professora. Svet uzhe
byl potushen, i auditoriya opustela. Razbudivshij ego universitetskij sluzhitel'
myagko zametil:
- My zakryvaemsya, ser! Esli hotite spat', stupajte luchshe k sebe domoj.
Mister Tompkins vstal i napravilsya k vyhodu.
lekciya professora o teorii otnositel'nosti, na kotoroj zasnul mister
Tompkins
Ledi i dzhentl'meny!
CHelovecheskij razum sformiroval opredelennye predstavleniya o
prostranstve i vremeni kak o vmestilishche ili arene, na kotoroj proishodyat
razlichnye sobytiya. |ti predstavleniya bez osobyh izmenenij peredavalis' iz
pokoleniya v pokolenie, a so vremeni zarozhdeniya tochnyh nauk byli vklyucheny v
samye osnovy matematicheskogo opisaniya okruzhayushchego nas mira. Velikij N'yuton,
po-vidimomu, pervym dal chetkuyu formulirovku klassicheskih ponyatij
prostranstva i vremeni, napisav v svoih "Matematicheskih nachalah":
"_Absolyutnoe prostranstvo_ po samoj svoej sushchnosti, bezotnositel'no k
chemu by to ni bylo vneshnemu, ostaetsya vsegda odinakovym i nepodvizhnym" i
"_Absolyutnoe, istinnoe matematicheskoe vremya_ samo po sebe i po samoj svoej
sushchnosti, bez vsyakogo otnosheniya k chemu-libo vneshnemu, protekaet ravnomerno i
inache nazyvaetsya dlitel'nost'yu" {N'yuton I. Matematicheskie nachala natural'noj
filosofii. - Per. s latinskogo i kommentarii A.N. Krylova. Predislovie
L.S.Polaka. - M.: Nauka, 1989. - S. 30. (Prim. per.)}.
- Ubezhdenie v absolyutnoj pravil'nosti etih klassicheskih predstavlenij o
prostranstve i vremeni bylo stol' sil'nym, chto filosofy chasto schitali ih
apriornymi i ni odnomu uchenomu-estestvoispytatelyu dazhe v golovu ne prihodilo
usomnit'sya v nih. Odnako v nachale XX veka stalo yasno, chto ryad rezul'tatov,
poluchennyh s pomoshch'yu chuvstvitel'nyh i tonkih metodov eksperimental'noj
fiziki, privodyat k protivorechiyam, esli ih interpretirovat' v ramkah
klassicheskih predstavlenij o prostranstve i vremeni. |to obstoyatel'stvo
privelo odnogo iz velichajshih sovremennyh fizikov Al'berta |jnshtejna k
revolyucionnoj idee: ne sushchestvuet nikakih prichin, krome tradicii, po kotorym
klassicheskie predstavleniya o prostranstve i vremeni sledovalo by schitat'
absolyutno pravil'nymi; v eti ponyatiya mozhno i dolzhno vnosit' izmeneniya, chtoby
oni sootvetstvovali nashemu novomu, bolee tochnomu opytu. Dejstvitel'no,
klassicheskie ponyatiya prostranstva i vremeni byli sformulirovany na osnove
chelovecheskogo opyta, pocherpnutogo iz povsednevnoj zhizni. Nuzhno li
udivlyat'sya, chto tonkie i tochnye sovremennye metody nablyudeniya, osnovannye na
ispol'zovanii vysokorazvitoj eksperimental'noj tehniki, ukazyvayut na to, chto
starye ponyatiya prostranstva i vremeni slishkom gruby, netochny i mogli
ispol'zovat'sya v povsednevnoj zhizni i na bolee rannih stadiyah razvitiya
fiziki tol'ko potomu, chto ih otkloneniya ot pravil'nyh ponyatij dostatochno
maly. Ne sleduet udivlyat'sya i tomu, chto rasshirenie oblasti issledovanij
sovremennoj nauki rano ili pozdno dolzhno bylo privesti nas v takie oblasti,
gde eti otkloneniya ves'ma veliki i klassicheskie ponyatiya voobshche ne primenimy.
Samym vazhnym eksperimental'nym rezul'tatom, privedshim k korennomu
peresmotru nashih klassicheskih predstavlenij, stalo otkrytie togo fakta, chto
skorost' sveta v pustote predstavlyaet soboj verhnij predel vseh vozmozhnyh
fizicheskih skorostej. Takoj vazhnyj i neozhidannyj vyvod byl sdelan glavnym
obrazom na osnovanii eksperimentov amerikanskogo fizika Majkel'sona, kotoryj
v konce proshlogo veka predprinyal popytku nablyudat' vliyanie dvizheniya Zemli na
skorost' rasprostraneniya sveta i k svoemu velikomu udivleniyu i k udivleniyu
vsego nauchnogo mira obnaruzhil, chto nikakih effektov, svidetel'stvuyushchih o
vliyanii skorosti dvizheniya Zemli na skorost' sveta, ne sushchestvuet i chto
skorost' sveta v pustote okazyvaetsya vsegda odnoj i toj zhe, nezavisimo ot
sistemy, v kotoroj proizvoditsya izmerenie, ili ot dvizheniya istochnika,
ispuskayushchego svet. Net neobhodimosti ob座asnyat', pochemu takoj rezul'tat
ves'ma neobychen i protivorechit nashim fundamental'nym predstavleniyam o
dvizhenii. Dejstvitel'no, esli kakoj-to ob容kt bystro dvizhetsya v
prostranstve, a vy dvizhetes' navstrechu emu, to dvizhushchijsya ob容kt stolknetsya
s vami s bol'shej otnositel'noj skorost'yu, ravnoj summe skorostej ob容kta i
nablyudatelya. S drugoj storony, esli vy udalyaetes' ot ob容kta, to on, dognav
vas szadi, stolknetsya s vami s men'shej otnositel'noj skorost'yu, ravnoj
raznosti skorostej.
Naprimer, esli vy dvizhetes', skazhem, edete v avtomashine, navstrechu
rasprostranyayushchemusya v vozduhe zvuku, to izmerennaya iz mashiny skorost' zvuka
budet bol'she na velichinu, ravnuyu skorosti, razvivaemoj vashej mashinoj, ili,
sootvetstvenno, men'she, esli zvuk dogonyaet vas. My nazyvaem eto _teoremoj
slozheniya skorostej_. Vsegda schitalos', chto eta teorema samoochevidna.
Odnako, kak pokazali samye tshchatel'nye eksperimenty, v sluchae sveta
teorema slozheniya skorostej narushaetsya: skorost' sveta v pustote vsegda
ostaetsya odnoj i toj zhe i ravna 300000 km/s (skorost' sveta prinyato
oboznachat' strochnoj latinskoj bukvoj s) nezavisimo ot togo, kak bystro
dvizhetsya nablyudatel'.
- Vse eto horosho, - skazhete vy, - no razve nel'zya postroit'
sverhsvetovuyu skorost', skladyvaya neskol'ko men'shih, fizicheski dostizhimyh
skorostej?
Mozhem zhe my predstavit' sebe dvizhushchijsya ochen' bystro (naprimer, so
skorost'yu, ravnoj 3/4 skorosti sveta) poezd i brodyagu, begushchego po krysham
vagonov takzhe so skorost'yu, ravnoj 3/4 skorosti sveta.
Po teoreme slozheniya skorostej, obshchaya skorost' brodyagi byla by ravna
polutora skorostyam sveta, i brodyaga mog by obognat' svet, ispuskaemyj
signal'nym fonarem. Odnako istina sostoit v tom, chto, poskol'ku postoyanstvo
skorosti sveta est' eksperimental'nyj fakt, rezul'tiruyushchaya skorost' v nashem
sluchae dolzhna byt' men'she, chem my ozhidaem, - ona ne mozhet prevoshodit'
kriticheskogo znacheniya s. Takim obrazom, my prihodim k vyvodu o tom, chto i
pri men'shih skorostyah klassicheskaya teorema slozheniya skorostej dolzhna byt'
neverna.
Matematicheskij analiz problemy, v kotoryj ya ne hochu zdes' vdavat'sya,
privodit k ochen' prostoj novoj formule dlya vychisleniya rezul'tiruyushchej
skorosti dvuh skladyvaemyh dvizhenij.
Esli u1 i u2 - dve podlezhashchie slozheniyu skorosti, to rezul'tiruyushchaya
skorost' okazyvaetsya ravnoj
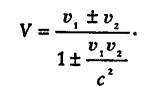 (1)
Vy vidite iz etoj formuly, chto esli obe podlezhashchie slozheniyu skorosti
maly (ya imeyu v vidu "maly po sravneniyu so skorost'yu sveta"), to vtorym
chlenom v znamenatele formuly (1) mozhno prenebrech' po sravneniyu s edinicej i
vy poluchaete klassicheskuyu teoremu slozheniya skorostej. Esli zhe skorosti u1, i
u2 ne maly, to rezul'tat budet neskol'ko men'she arifmeticheskoj summy
skorostej. Tak, v nashem primere s brodyagoj, begushchim po krysham vagonov
mchashchegosya poezda, u1 = (3/4)c i u2 = (3/4)c i nasha formula pozvolyaet najti
rezul'tiruyushchuyu skorost' F = (24/25) s, kotoraya, kak i skladyvaemye skorosti,
men'she skorosti sveta.
V chastnosti, kogda odna iz ishodnyh skorostej ravna skorosti sveta s,
iz formuly (1) sleduet, chto rezul'tiruyushchaya skorost' takzhe ravna s,
nezavisimo ot togo, kakova vtoraya skorost'. Poetomu, skladyvaya lyuboe chislo
skorostej, my nikogda ne mozhem prevzojti skorost' sveta.
Vozmozhno, vam budet interesno uznat', chto formula (1) byla podtverzhdena
eksperimental'no i dejstvitel'no bylo obnaruzheno, chto rezul'tiruyushchaya dvuh
skorostej vsegda neskol'ko men'she ih arifmeticheskoj summy.
(1)
Vy vidite iz etoj formuly, chto esli obe podlezhashchie slozheniyu skorosti
maly (ya imeyu v vidu "maly po sravneniyu so skorost'yu sveta"), to vtorym
chlenom v znamenatele formuly (1) mozhno prenebrech' po sravneniyu s edinicej i
vy poluchaete klassicheskuyu teoremu slozheniya skorostej. Esli zhe skorosti u1, i
u2 ne maly, to rezul'tat budet neskol'ko men'she arifmeticheskoj summy
skorostej. Tak, v nashem primere s brodyagoj, begushchim po krysham vagonov
mchashchegosya poezda, u1 = (3/4)c i u2 = (3/4)c i nasha formula pozvolyaet najti
rezul'tiruyushchuyu skorost' F = (24/25) s, kotoraya, kak i skladyvaemye skorosti,
men'she skorosti sveta.
V chastnosti, kogda odna iz ishodnyh skorostej ravna skorosti sveta s,
iz formuly (1) sleduet, chto rezul'tiruyushchaya skorost' takzhe ravna s,
nezavisimo ot togo, kakova vtoraya skorost'. Poetomu, skladyvaya lyuboe chislo
skorostej, my nikogda ne mozhem prevzojti skorost' sveta.
Vozmozhno, vam budet interesno uznat', chto formula (1) byla podtverzhdena
eksperimental'no i dejstvitel'no bylo obnaruzheno, chto rezul'tiruyushchaya dvuh
skorostej vsegda neskol'ko men'she ih arifmeticheskoj summy.
 Priznav sushchestvovanie verhnego predela skorosti, my mozhem pristupit' k
analizu klassicheskih predstavlenij o prostranstve i vremeni. Svoj pervyj
udar my napravim protiv ponyatiya _odnovremennosti_, osnovannom na etih
klassicheskih predstavleniyah. Kogda vy zayavlyaete:
- Vzryv na shahte nepodaleku ot Kejptauna proizoshel v tot samyj moment,
kogda v moej londonskoj kvartire mne na zavtrak podali yaichnicu s vetchinoj, -
vam kazhetsya, budto vy vyskazyvaete vpolne osmyslennoe utverzhdenie. Odnako ya
popytayus' pokazat', chto v dejstvitel'nosti vy ne znaete, o chem, sobstvenno,
idet rech' i, bolee togo, chto vashe utverzhdenie, strogo govorya, ne imeet
tochnogo smysla. V samom dele, kak by vy stali proveryat' odnovremennost' dvuh
sobytij, proishodyashchih v dvuh razlichnyh mestah? Vozmozhno, vy skazhete, chto
takie dva sobytiya odnovremenny, esli mestnye chasy pokazyvayut odno i to zhe
vremya, no togda voznikaet vopros, kak ustanovit' chasy, raznesennye v
prostranstve na bol'shoe rasstoyanie drug ot druga, tak, chtoby oni
odnovremenno pokazyvali odno i to zhe vremya, i my snova vozvrashchaemsya k
ishodnomu voprosu.
Poskol'ku nezavisimost' skorosti sveta v pustote ot dvizheniya istochnika
ili sistemy, v kotoroj proizvoditsya izmerenie, prinadlezhit k chislu naibolee
tochno ustanovlennyh eksperimental'nyh faktov, sleduyushchij metod izmereniya
rasstoyanij i pravil'noj ustanovki chasov na razlichnyh nablyudatel'nyh stanciyah
sleduet priznat' naibolee razumnym i, porazmysliv nemnogo, vy soglasites' so
mnoj, chto eto - edinstvenno priemlemyj sposob.
Svetovoj signal otpravlyaetsya so stancii A i, kak tol'ko on prinimaetsya
na stancii V, posylaetsya obratno na stanciyu A. Polovina vremeni (po
izmereniyam, proizvodimym na stancii A) mezhdu otpravleniem signala i ego
priemom na stancii A, umnozhennaya na skorost' sveta, opredelyaet rasstoyanie
mezhdu stanciyami A i V.
Uslovimsya govorit', chto chasy na stanciyah A i V ustanovleny pravil'no,
esli v moment priema signala na stancii V mestnye chasy pokazyvali vremya,
ravnoe polusumme pokazanij chasov na stancii A v moment otpravleniya i priema
signala. Primenyaya etot sposob pravil'noj ustanovki chasov k dvum razlichnym
nablyudatel'nym stanciyam, sooruzhennym na odnoj platforme (odnom i tom zhe
tverdom tele), my poluchaem stol' zhelannuyu sistemu otscheta i obretaem
vozmozhnost' otvechat' na voprosy ob odnovremennosti sobytij ili vremenn_o_m
intervale mezhdu dvumya sobytiyami, proishodyashchimi v razlichnyh mestah.
No priznayut li odnovremennymi te zhe sobytiya i soglasyatsya li s ocenkoj
vremennyh intervalov nablyudateli v drugih sistemah otscheta? CHtoby otvetit'
na etot vopros, predstavim sebe dve sistemy otscheta, sooruzhennye na dvuh
razlichnyh platformah (tverdyh telah), naprimer na dvuh dlinnyh kosmicheskih
raketah, letyashchih v protivopolozhnyh napravleniyah kazhdaya so svoej postoyannoj
skorost'yu. Kak rezul'taty izmerenij, proizvodimyh v odnoj sisteme otscheta,
budut sootnosit'sya s rezul'tatami analogichnyh izmerenij, proizvodimyh v
drugoj sisteme otscheta? Predpolozhim, chto v nosovoj i kormovoj chasti kazhdoj
rakety nahoditsya po nablyudatelyu i chto vse chetyre nablyudatelya hotyat prezhde
vsego pravil'no ustanovit' svoi chasy. Kazhdaya para nablyudatelej, nahodyashchihsya
na bortu odnoj i toj zhe rakety, mozhet, neskol'ko vidoizmeniv opisannyj vyshe
sposob pravil'noj ustanovki chasov, postavit' nul' na svoih chasah v tot
moment, kogda svetovoj signal, poslannyj iz serediny rakety (seredina rakety
mozhet byt' ustanovlena s pomoshch'yu mernogo sterzhnya), dostignet sootvetstvenno
nosa ili kormy rakety. Takim obrazom, kazhdaya para nashih nablyudatelej
ustanavlivaet v sootvetstvii s prinyatym vyshe opredeleniem kriterij
odnovremennosti v svoej sobstvennoj sisteme otscheta i "pravil'no"
(razumeetsya, so svoej tochki zreniya) svoi chasy.
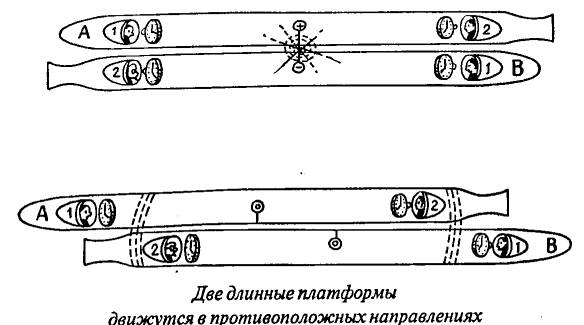
Predpolozhim teper', chto nashi nablyudateli reshili vyyasnit', soglasuyutsya
li pokazaniya chasov na bortu ih rakety s pokazaniem chasov na bortu drugoj
rakety. Naprimer, budut li chasy dvuh nablyudatelej, nahodyashchihsya na bortu
razlichnyh raket, pokazyvat' odno i to zhe vremya, kogda raketam sluchitsya
proletat' mimo drug druga? Proverit' eto mozhno sleduyushchim sposobom. V centre
(geometricheskoj seredine) kazhdoj rakety nablyudateli, ustanavlivayut
zaryazhennyj kondensator s takim raschetom, chto kogda rakety proletayut mimo
drug druga, mezhdu kondensatorami proskakivaet iskra i iz centra kazhdoj
platformy k ee koncam (nosu i korme) odnovremenno nachinayut rasprostranyat'sya
svetovye signaly. K tomu vremeni, kogda svetovye signaly, rasprostranyayushchiesya
s konechnoj skorost'yu, dostignut nablyudatelej, rakety izmenyat svoe
otnositel'noe raspolozhenie i nablyudateli 2A i 2V okazhutsya blizhe k istochniku
sveta, chem nablyudateli 1A i 1V.
YAsno, chto kogda svetovoj signal dostignet nablyudatelya 2A, nablyudatel'
1B budet pozadi nego i, chtoby dostignut' nablyudatelya 1B, svetovomu signalu
ponadobitsya nekotoroe dopolnitel'noe vremya. Sledovatel'no, esli chasy
nablyudatelya 1V postavleny tak, chto pokazyvayut nol' chasov nol' minut v moment
prihoda signala, to nablyudatel' 2A budet nastaivat' na tom, chto chasy ego
kollegi 1V otstayut ot pravil'nogo vremeni.
Tochno tak zhe drugoj nablyudatel' 1A pridet k zaklyucheniyu, chto chasy
nablyudatelya 2V, do kotorogo svetovoj signal dojdet ran'she, chem do nego,
speshat. Poskol'ku soglasno prinyatomu opredeleniyu odnovremennosti kazhdyj iz
nablyudatelej schitaet, chto ego chasy postavleny pravil'no, nablyudateli na
bortu rakety A soglasyatsya s tem, chto mezhdu chasami nablyudatelej na bortu
rakety V imeetsya razlichie. Ne sleduet, odnako, zabyvat' o tom, chto
nablyudateli na bortu rakety V po tochno tem zhe prichinam budut schitat', chto ih
chasy postavleny pravil'no, a chasy nablyudatelej na bortu rakety A
rassoglasovany.
Poskol'ku obe rakety sovershenno ekvivalentny, raznoglasiya mezhdu dvumya
gruppami nablyudatelej mozhno razreshit', tol'ko esli priznat', chto pravy obe
gruppy - kazhdaya so svoej tochki zreniya, no chto vopros o tom, kto iz nih prav,
"absolyutno" ne imeet fizicheskogo smysla.
Boyus' chto ya utomil vas etimi dlinnymi rassuzhdeniyami, no esli vy
vnimatel'no sledili za hodom moej mysli, to vam dolzhno byt' yasno, chto kak
tol'ko nash sposob prostranstvenno-vremenn_y_h izmerenij prinyat, _ponyatie
absolyutnoj odnovremennosti polnost'yu utrachivaet smysl i dva sobytiya,
proishodyashchie v razlichnyh mestah i odnovremennye s tochki zreniya odnoj sistemy
otscheta, razdeleny konechnym vremennym intervalom s tochki zreniya drugoj
sistemy otscheta_.
|to utverzhdenie zvuchit ves'ma stranno, v osobennosti dlya teh, kto
slyshit ego vpervye, no tak li stranno pokazhetsya vam, esli ya skazhu, chto,
obedaya v vagone-restorane idushchego poezda, vy s容daete svoj sup i desert v
odnoj i toj zhe tochke vagona-restorana, no v razlichnyh tochkah
zheleznodorozhnogo polotna, razdelennyh dostatochno bol'shim rasstoyaniem? Mezhdu
tem utverzhdenie o vashej trapeze v poezde mozhno sformulirovat' i tak: _dva
sobytiya, proishodyashchie v razlichnoe vremya v odnoj i toj zhe tochke odnoj sistemy
otscheta, razdeleny konechnym prostranstvennym intervalom s tochki zreniya
drugoj sistemy otscheta_.
Sravniv eto "trivial'noe" utverzhdenie s predydushchim "paradoksal'nym"
utverzhdeniem, vy uvidite, chto oni sovershenno simmetrichny i perehodyat drug v
druga, esli slovo "vremennoj" zamenit' na "prostranstvennyj" (i naoborot).
V etom i sostoit vsya sut' tochki zreniya |jnshtejna: esli v klassicheskoj
fizike vremya rassmatrivalos' kak nechto sovershenno nezavisimoe ot
prostranstva i dvizheniya i schitalos', chto ono "po samoj svoej sushchnosti, bez
vsyakogo otnosheniya k chemu-libo vneshnemu, protekaet ravnomerno" (N'yuton), to v
novoj fizike prostranstvo i vremya tesno vzaimosvyazany i predstavlyayut soboj
dva razlichnyh secheniya odnogo odnorodnogo "prostranstvenno-vremennogo
kontinuuma", v kotorom razygryvayutsya vse nablyudaemye sobytiya. Razdelenie
etogo chetyrehmernogo kontinuuma na trehmernoe prostranstvo i odnomernoe
vremya sovershenno proizvol'no i zavisit ot sistemy otscheta, v kotoroj
proizvodyatsya nablyudeniya.
Dva sobytiya, razdelennye v prostranstve rasstoyaniem l i vo vremeni
intervalom t po nablyudeniyam v odnoj sisteme otscheta, po nablyudeniyam v drugoj
sisteme otscheta razdeleny drugim rasstoyaniem l' v prostranstve i drugim
vremennym intervalom t' chto pozvolyaet v opredelennom smysle govorit' o
preobrazovanii prostranstva vo vremya i naoborot. Netrudno takzhe ponyat',
pochemu preobrazovanie vremeni v prostranstvo, kak v primere s obedom v
vagone-restorane, dlya nas obychnoe delo, togda kak preobrazovanie
prostranstva vo vremya, porozhdayushchee otnositel'nost' ponyatiya odnovremennosti,
kazhetsya ves'ma neobychnym. Delo v tom, chto esli rasstoyaniya my izmeryaem,
naprimer, v "santimetrah", to sootvetstvuyushchej edinicej vremeni dolzhna byt'
ne privychnaya "sekunda", a "racional'naya edinica vremeni" - interval vremeni,
kotoryj neobhodim svetovomu signalu dlya togo, chtoby preodolet' rasstoyanie v
odin santimetr, t.e. 0,00000000003 sekundy.
Sledovatel'no, v sfere nashego obychnogo opyta preobrazovanie
prostranstvennyh intervalov vo vremennye intervaly privodit k prakticheski
nenablyudaemym rezul'tatam, chto, kazalos' by, podkreplyaet klassicheskij vzglyad
na prirodu veshchej, soglasno kotoromu vremya est' nechto absolyutno nezavisimoe i
neizmenyaemoe.
No pri izuchenii dvizhenij s ochen' bol'shimi skorostyami, naprimer,
dvizheniya elektronov, ispuskaemyh radioaktivnymi elementami, ili dvizheniya
elektronov vnutri atoma, gde rasstoyaniya, pokryvaemye za opredelennyj
interval vremeni, - velichiny togo zhe poryadka, kak vremya, vyrazhennoe v
racional'nyh edinicah, my nepremenno stalkivaemsya s oboimi effektami, o
kotoryh shla rech' vyshe, i teoriya otnositel'nosti priobretaet vazhnoe znachenie.
Relyativistskie effekty mogut nablyudat'sya dazhe v oblasti sravnitel'no malyh
skorostej, naprimer, pri dvizhenii planet v nashej Solnechnoj sisteme iz-za
neobychajno vysokoj tochnosti astronomicheskih izmerenij (odnako nablyudenie
relyativistskih effektov v podobnyh sluchayah trebuet izmerenij izmenenij
dvizheniya planety, dohodyashchih do doli uglovoj sekundy za god).
Kak ya pytalsya ob座asnit' vam, kriticheskij analiz ponyatij prostranstva i
vremeni privodit k zaklyucheniyu, chto prostranstvennye intervaly mogut byt'
chastichno prevrashcheny vo vremennye intervaly i naoborot. |to oznachaet, chto
chislovye znacheniya dannogo rasstoyaniya ili perioda vremeni, izmeryaemye v
razlichnyh dvizhushchihsya sistemah otscheta, mogut rashodit'sya.
Sravnitel'no prostoj matematicheskij analiz etoj problemy, v kotoryj,
odnako, ya ne hotel by vhodit' na etih lekciyah, privodit k vpolne
opredelennym formulam dlya izmeneniya dlin prostranstvennyh i vremenn_y_h
intervalov. Iz nih sleduet, chto lyuboj ob容kt dliny l, dvizhushchijsya
otnositel'no nablyudatelya so skorost'yu u, sokratitsya na velichinu, zavisyashchuyu
ot skorosti, i izmerennaya dlina ob容kta okazhetsya ravnoj
Priznav sushchestvovanie verhnego predela skorosti, my mozhem pristupit' k
analizu klassicheskih predstavlenij o prostranstve i vremeni. Svoj pervyj
udar my napravim protiv ponyatiya _odnovremennosti_, osnovannom na etih
klassicheskih predstavleniyah. Kogda vy zayavlyaete:
- Vzryv na shahte nepodaleku ot Kejptauna proizoshel v tot samyj moment,
kogda v moej londonskoj kvartire mne na zavtrak podali yaichnicu s vetchinoj, -
vam kazhetsya, budto vy vyskazyvaete vpolne osmyslennoe utverzhdenie. Odnako ya
popytayus' pokazat', chto v dejstvitel'nosti vy ne znaete, o chem, sobstvenno,
idet rech' i, bolee togo, chto vashe utverzhdenie, strogo govorya, ne imeet
tochnogo smysla. V samom dele, kak by vy stali proveryat' odnovremennost' dvuh
sobytij, proishodyashchih v dvuh razlichnyh mestah? Vozmozhno, vy skazhete, chto
takie dva sobytiya odnovremenny, esli mestnye chasy pokazyvayut odno i to zhe
vremya, no togda voznikaet vopros, kak ustanovit' chasy, raznesennye v
prostranstve na bol'shoe rasstoyanie drug ot druga, tak, chtoby oni
odnovremenno pokazyvali odno i to zhe vremya, i my snova vozvrashchaemsya k
ishodnomu voprosu.
Poskol'ku nezavisimost' skorosti sveta v pustote ot dvizheniya istochnika
ili sistemy, v kotoroj proizvoditsya izmerenie, prinadlezhit k chislu naibolee
tochno ustanovlennyh eksperimental'nyh faktov, sleduyushchij metod izmereniya
rasstoyanij i pravil'noj ustanovki chasov na razlichnyh nablyudatel'nyh stanciyah
sleduet priznat' naibolee razumnym i, porazmysliv nemnogo, vy soglasites' so
mnoj, chto eto - edinstvenno priemlemyj sposob.
Svetovoj signal otpravlyaetsya so stancii A i, kak tol'ko on prinimaetsya
na stancii V, posylaetsya obratno na stanciyu A. Polovina vremeni (po
izmereniyam, proizvodimym na stancii A) mezhdu otpravleniem signala i ego
priemom na stancii A, umnozhennaya na skorost' sveta, opredelyaet rasstoyanie
mezhdu stanciyami A i V.
Uslovimsya govorit', chto chasy na stanciyah A i V ustanovleny pravil'no,
esli v moment priema signala na stancii V mestnye chasy pokazyvali vremya,
ravnoe polusumme pokazanij chasov na stancii A v moment otpravleniya i priema
signala. Primenyaya etot sposob pravil'noj ustanovki chasov k dvum razlichnym
nablyudatel'nym stanciyam, sooruzhennym na odnoj platforme (odnom i tom zhe
tverdom tele), my poluchaem stol' zhelannuyu sistemu otscheta i obretaem
vozmozhnost' otvechat' na voprosy ob odnovremennosti sobytij ili vremenn_o_m
intervale mezhdu dvumya sobytiyami, proishodyashchimi v razlichnyh mestah.
No priznayut li odnovremennymi te zhe sobytiya i soglasyatsya li s ocenkoj
vremennyh intervalov nablyudateli v drugih sistemah otscheta? CHtoby otvetit'
na etot vopros, predstavim sebe dve sistemy otscheta, sooruzhennye na dvuh
razlichnyh platformah (tverdyh telah), naprimer na dvuh dlinnyh kosmicheskih
raketah, letyashchih v protivopolozhnyh napravleniyah kazhdaya so svoej postoyannoj
skorost'yu. Kak rezul'taty izmerenij, proizvodimyh v odnoj sisteme otscheta,
budut sootnosit'sya s rezul'tatami analogichnyh izmerenij, proizvodimyh v
drugoj sisteme otscheta? Predpolozhim, chto v nosovoj i kormovoj chasti kazhdoj
rakety nahoditsya po nablyudatelyu i chto vse chetyre nablyudatelya hotyat prezhde
vsego pravil'no ustanovit' svoi chasy. Kazhdaya para nablyudatelej, nahodyashchihsya
na bortu odnoj i toj zhe rakety, mozhet, neskol'ko vidoizmeniv opisannyj vyshe
sposob pravil'noj ustanovki chasov, postavit' nul' na svoih chasah v tot
moment, kogda svetovoj signal, poslannyj iz serediny rakety (seredina rakety
mozhet byt' ustanovlena s pomoshch'yu mernogo sterzhnya), dostignet sootvetstvenno
nosa ili kormy rakety. Takim obrazom, kazhdaya para nashih nablyudatelej
ustanavlivaet v sootvetstvii s prinyatym vyshe opredeleniem kriterij
odnovremennosti v svoej sobstvennoj sisteme otscheta i "pravil'no"
(razumeetsya, so svoej tochki zreniya) svoi chasy.
Predpolozhim teper', chto nashi nablyudateli reshili vyyasnit', soglasuyutsya
li pokazaniya chasov na bortu ih rakety s pokazaniem chasov na bortu drugoj
rakety. Naprimer, budut li chasy dvuh nablyudatelej, nahodyashchihsya na bortu
razlichnyh raket, pokazyvat' odno i to zhe vremya, kogda raketam sluchitsya
proletat' mimo drug druga? Proverit' eto mozhno sleduyushchim sposobom. V centre
(geometricheskoj seredine) kazhdoj rakety nablyudateli, ustanavlivayut
zaryazhennyj kondensator s takim raschetom, chto kogda rakety proletayut mimo
drug druga, mezhdu kondensatorami proskakivaet iskra i iz centra kazhdoj
platformy k ee koncam (nosu i korme) odnovremenno nachinayut rasprostranyat'sya
svetovye signaly. K tomu vremeni, kogda svetovye signaly, rasprostranyayushchiesya
s konechnoj skorost'yu, dostignut nablyudatelej, rakety izmenyat svoe
otnositel'noe raspolozhenie i nablyudateli 2A i 2V okazhutsya blizhe k istochniku
sveta, chem nablyudateli 1A i 1V.
YAsno, chto kogda svetovoj signal dostignet nablyudatelya 2A, nablyudatel'
1B budet pozadi nego i, chtoby dostignut' nablyudatelya 1B, svetovomu signalu
ponadobitsya nekotoroe dopolnitel'noe vremya. Sledovatel'no, esli chasy
nablyudatelya 1V postavleny tak, chto pokazyvayut nol' chasov nol' minut v moment
prihoda signala, to nablyudatel' 2A budet nastaivat' na tom, chto chasy ego
kollegi 1V otstayut ot pravil'nogo vremeni.
Tochno tak zhe drugoj nablyudatel' 1A pridet k zaklyucheniyu, chto chasy
nablyudatelya 2V, do kotorogo svetovoj signal dojdet ran'she, chem do nego,
speshat. Poskol'ku soglasno prinyatomu opredeleniyu odnovremennosti kazhdyj iz
nablyudatelej schitaet, chto ego chasy postavleny pravil'no, nablyudateli na
bortu rakety A soglasyatsya s tem, chto mezhdu chasami nablyudatelej na bortu
rakety V imeetsya razlichie. Ne sleduet, odnako, zabyvat' o tom, chto
nablyudateli na bortu rakety V po tochno tem zhe prichinam budut schitat', chto ih
chasy postavleny pravil'no, a chasy nablyudatelej na bortu rakety A
rassoglasovany.
Poskol'ku obe rakety sovershenno ekvivalentny, raznoglasiya mezhdu dvumya
gruppami nablyudatelej mozhno razreshit', tol'ko esli priznat', chto pravy obe
gruppy - kazhdaya so svoej tochki zreniya, no chto vopros o tom, kto iz nih prav,
"absolyutno" ne imeet fizicheskogo smysla.
Boyus' chto ya utomil vas etimi dlinnymi rassuzhdeniyami, no esli vy
vnimatel'no sledili za hodom moej mysli, to vam dolzhno byt' yasno, chto kak
tol'ko nash sposob prostranstvenno-vremenn_y_h izmerenij prinyat, _ponyatie
absolyutnoj odnovremennosti polnost'yu utrachivaet smysl i dva sobytiya,
proishodyashchie v razlichnyh mestah i odnovremennye s tochki zreniya odnoj sistemy
otscheta, razdeleny konechnym vremennym intervalom s tochki zreniya drugoj
sistemy otscheta_.
|to utverzhdenie zvuchit ves'ma stranno, v osobennosti dlya teh, kto
slyshit ego vpervye, no tak li stranno pokazhetsya vam, esli ya skazhu, chto,
obedaya v vagone-restorane idushchego poezda, vy s容daete svoj sup i desert v
odnoj i toj zhe tochke vagona-restorana, no v razlichnyh tochkah
zheleznodorozhnogo polotna, razdelennyh dostatochno bol'shim rasstoyaniem? Mezhdu
tem utverzhdenie o vashej trapeze v poezde mozhno sformulirovat' i tak: _dva
sobytiya, proishodyashchie v razlichnoe vremya v odnoj i toj zhe tochke odnoj sistemy
otscheta, razdeleny konechnym prostranstvennym intervalom s tochki zreniya
drugoj sistemy otscheta_.
Sravniv eto "trivial'noe" utverzhdenie s predydushchim "paradoksal'nym"
utverzhdeniem, vy uvidite, chto oni sovershenno simmetrichny i perehodyat drug v
druga, esli slovo "vremennoj" zamenit' na "prostranstvennyj" (i naoborot).
V etom i sostoit vsya sut' tochki zreniya |jnshtejna: esli v klassicheskoj
fizike vremya rassmatrivalos' kak nechto sovershenno nezavisimoe ot
prostranstva i dvizheniya i schitalos', chto ono "po samoj svoej sushchnosti, bez
vsyakogo otnosheniya k chemu-libo vneshnemu, protekaet ravnomerno" (N'yuton), to v
novoj fizike prostranstvo i vremya tesno vzaimosvyazany i predstavlyayut soboj
dva razlichnyh secheniya odnogo odnorodnogo "prostranstvenno-vremennogo
kontinuuma", v kotorom razygryvayutsya vse nablyudaemye sobytiya. Razdelenie
etogo chetyrehmernogo kontinuuma na trehmernoe prostranstvo i odnomernoe
vremya sovershenno proizvol'no i zavisit ot sistemy otscheta, v kotoroj
proizvodyatsya nablyudeniya.
Dva sobytiya, razdelennye v prostranstve rasstoyaniem l i vo vremeni
intervalom t po nablyudeniyam v odnoj sisteme otscheta, po nablyudeniyam v drugoj
sisteme otscheta razdeleny drugim rasstoyaniem l' v prostranstve i drugim
vremennym intervalom t' chto pozvolyaet v opredelennom smysle govorit' o
preobrazovanii prostranstva vo vremya i naoborot. Netrudno takzhe ponyat',
pochemu preobrazovanie vremeni v prostranstvo, kak v primere s obedom v
vagone-restorane, dlya nas obychnoe delo, togda kak preobrazovanie
prostranstva vo vremya, porozhdayushchee otnositel'nost' ponyatiya odnovremennosti,
kazhetsya ves'ma neobychnym. Delo v tom, chto esli rasstoyaniya my izmeryaem,
naprimer, v "santimetrah", to sootvetstvuyushchej edinicej vremeni dolzhna byt'
ne privychnaya "sekunda", a "racional'naya edinica vremeni" - interval vremeni,
kotoryj neobhodim svetovomu signalu dlya togo, chtoby preodolet' rasstoyanie v
odin santimetr, t.e. 0,00000000003 sekundy.
Sledovatel'no, v sfere nashego obychnogo opyta preobrazovanie
prostranstvennyh intervalov vo vremennye intervaly privodit k prakticheski
nenablyudaemym rezul'tatam, chto, kazalos' by, podkreplyaet klassicheskij vzglyad
na prirodu veshchej, soglasno kotoromu vremya est' nechto absolyutno nezavisimoe i
neizmenyaemoe.
No pri izuchenii dvizhenij s ochen' bol'shimi skorostyami, naprimer,
dvizheniya elektronov, ispuskaemyh radioaktivnymi elementami, ili dvizheniya
elektronov vnutri atoma, gde rasstoyaniya, pokryvaemye za opredelennyj
interval vremeni, - velichiny togo zhe poryadka, kak vremya, vyrazhennoe v
racional'nyh edinicah, my nepremenno stalkivaemsya s oboimi effektami, o
kotoryh shla rech' vyshe, i teoriya otnositel'nosti priobretaet vazhnoe znachenie.
Relyativistskie effekty mogut nablyudat'sya dazhe v oblasti sravnitel'no malyh
skorostej, naprimer, pri dvizhenii planet v nashej Solnechnoj sisteme iz-za
neobychajno vysokoj tochnosti astronomicheskih izmerenij (odnako nablyudenie
relyativistskih effektov v podobnyh sluchayah trebuet izmerenij izmenenij
dvizheniya planety, dohodyashchih do doli uglovoj sekundy za god).
Kak ya pytalsya ob座asnit' vam, kriticheskij analiz ponyatij prostranstva i
vremeni privodit k zaklyucheniyu, chto prostranstvennye intervaly mogut byt'
chastichno prevrashcheny vo vremennye intervaly i naoborot. |to oznachaet, chto
chislovye znacheniya dannogo rasstoyaniya ili perioda vremeni, izmeryaemye v
razlichnyh dvizhushchihsya sistemah otscheta, mogut rashodit'sya.
Sravnitel'no prostoj matematicheskij analiz etoj problemy, v kotoryj,
odnako, ya ne hotel by vhodit' na etih lekciyah, privodit k vpolne
opredelennym formulam dlya izmeneniya dlin prostranstvennyh i vremenn_y_h
intervalov. Iz nih sleduet, chto lyuboj ob容kt dliny l, dvizhushchijsya
otnositel'no nablyudatelya so skorost'yu u, sokratitsya na velichinu, zavisyashchuyu
ot skorosti, i izmerennaya dlina ob容kta okazhetsya ravnoj
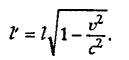 (2)
Analogichno, lyuboj process, dlyashchijsya vremya t, pri nablyudenii iz
dvizhushchejsya otnositel'no nego sistemy otscheta, budet dlit'sya dol'she - vremya
t', kotoroe mozhet byt' vychisleno po formule
(2)
Analogichno, lyuboj process, dlyashchijsya vremya t, pri nablyudenii iz
dvizhushchejsya otnositel'no nego sistemy otscheta, budet dlit'sya dol'she - vremya
t', kotoroe mozhet byt' vychisleno po formule
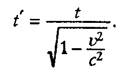 (3)
|to i est' znamenitoe "sokrashchenie prostranstva" i "zamedlenie vremeni"
v teorii otnositel'nosti.
Obychno, kogda skorost' u gorazdo men'she skorosti sveta s, eti effekty
ochen' maly, no pri dostatochno bol'shih skorostyah dliny, nablyudaemye iz
dvizhushchejsya sistemy otscheta, mogut byt' sdelany skol' ugodno malymi, a
vremenn_y_e intervaly - skol' ugodno prodolzhitel'nymi.
YA hochu, chtoby vy ne zabyvali, chto oba effekta - i sokrashchenie
prostranstvennyh intervalov, i zamedlenie vremeni - sovershenno simmetrichny
i, esli passazhiry bystro mchashchegosya poezda budut udivlyat'sya, pochemu passazhiry
stoyashchego poezda takie toshchie i dvizhutsya tak medlenno, passazhiry stoyashchego
poezda budut razmyshlyat' o tom zhe, glyadya na passazhirov mchashchegosya poezda.
Eshche odno sledstvie sushchestvovaniya maksimal'noj dostizhimoj skorosti
otnositsya k masse dvizhushchihsya tel. Kak yavstvuet iz obshchih osnov mehaniki,
massa tela opredelyaet, naskol'ko trudno privesti ego v dvizhenie ili, esli
ono uzhe dvizhetsya, uskorit' ego: chem bol'she massa, tem trudnee uvelichit'
skorost' tela na dannuyu velichinu.
To, chto ni odno telo ni pri kakih obstoyatel'stvah ne mozhet dvigat'sya so
skorost'yu, bol'shej skorosti sveta, privodit nas neposredstvenno k vyvodu,
chto ego soprotivlenie dal'nejshemu uskoreniyu, ili, inache govorya, ego massa,
neogranichenno vozrastaet, kogda skorost' tela priblizhaetsya k skorosti sveta.
Matematicheskij analiz pozvolyaet vyvesti formulu zavisimosti massy tela ot
ego skorosti, analogichnuyu formulam (2) i (3). Esli m0 - massa tela pri ochen'
malyh skorostyah, to massa m tela pri skorosti u opredelyaetsya po formule
(3)
|to i est' znamenitoe "sokrashchenie prostranstva" i "zamedlenie vremeni"
v teorii otnositel'nosti.
Obychno, kogda skorost' u gorazdo men'she skorosti sveta s, eti effekty
ochen' maly, no pri dostatochno bol'shih skorostyah dliny, nablyudaemye iz
dvizhushchejsya sistemy otscheta, mogut byt' sdelany skol' ugodno malymi, a
vremenn_y_e intervaly - skol' ugodno prodolzhitel'nymi.
YA hochu, chtoby vy ne zabyvali, chto oba effekta - i sokrashchenie
prostranstvennyh intervalov, i zamedlenie vremeni - sovershenno simmetrichny
i, esli passazhiry bystro mchashchegosya poezda budut udivlyat'sya, pochemu passazhiry
stoyashchego poezda takie toshchie i dvizhutsya tak medlenno, passazhiry stoyashchego
poezda budut razmyshlyat' o tom zhe, glyadya na passazhirov mchashchegosya poezda.
Eshche odno sledstvie sushchestvovaniya maksimal'noj dostizhimoj skorosti
otnositsya k masse dvizhushchihsya tel. Kak yavstvuet iz obshchih osnov mehaniki,
massa tela opredelyaet, naskol'ko trudno privesti ego v dvizhenie ili, esli
ono uzhe dvizhetsya, uskorit' ego: chem bol'she massa, tem trudnee uvelichit'
skorost' tela na dannuyu velichinu.
To, chto ni odno telo ni pri kakih obstoyatel'stvah ne mozhet dvigat'sya so
skorost'yu, bol'shej skorosti sveta, privodit nas neposredstvenno k vyvodu,
chto ego soprotivlenie dal'nejshemu uskoreniyu, ili, inache govorya, ego massa,
neogranichenno vozrastaet, kogda skorost' tela priblizhaetsya k skorosti sveta.
Matematicheskij analiz pozvolyaet vyvesti formulu zavisimosti massy tela ot
ego skorosti, analogichnuyu formulam (2) i (3). Esli m0 - massa tela pri ochen'
malyh skorostyah, to massa m tela pri skorosti u opredelyaetsya po formule
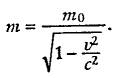 (4)
My vidim, chto soprotivlenie tela dal'nejshemu uskoreniyu stanovitsya
beskonechno bol'shim, kogda i stremitsya k c. |tot effekt relyativistskogo
izmeneniya massy mozhet byt' legko nablyudaem eksperimental'no na chasticah,
dvizhushchihsya s ochen' bol'shimi skorostyami. Naprimer, massa elektronov,
ispuskaemyh radioaktivnymi telami (so skorost'yu, sostavlyayushchej 99 % skorosti
sveta), v neskol'ko raz bol'she, chem v sostoyanii pokoya, a massy elektronov,
obrazuyushchih tak nazyvaemye kosmicheskie livni i neredko dvizhushchihsya so
skorost'yu 99,98 % skorosti sveta, v 1000 raz bol'she. K takim skorostyam
klassicheskaya mehanika stanovitsya absolyutno neprimenimoj, i my vstupaem v
oblast' chistoj teorii otnositel'nosti.
Mister Tompkins beret otpusk
Misteru Tompkinsu ochen' ponravilis' priklyucheniya v relyativistskom
gorode, ogorchalo tol'ko, chto s nim ne bylo professora, kotoryj mog by
ob座asnit' neobychnye yavleniya, kotorye emu, misteru Tompkinsu, dovelos' tam
nablyudat', naprimer, pomoch' razreshit' zagadku, osobenno zanimavshuyu ego:
kakim obrazom tormoznomu konduktoru udavalos' predupredit' starenie
passazhirov? Mnogo nochej podryad mister Tompkins ukladyvalsya v postel' s
nadezhdoj snova uvidet' polyubivshijsya emu gorod, no sny mister Tompkins videl
redko i, v osnovnom, dovol'no nepriyatnye. Naprimer, v poslednij raz misteru
Tompkinsu prisnilos', chto upravlyayushchij bankom uvolil ego za nebrezhnost' v
vedenii bankovskih schetov. Prosnuvshis', mister Tompkins schel za blago vzyat'
otpusk i otpravit'sya na nedel'ku kuda-nibud' na more. Tak mister Tompkins
okazalsya v kupe poezda, nablyudaya v okno, kak serye kryshi prigoroda
postepenno ustupayut mesto zelenym luzhajkam sel'skoj mestnosti. Mister
Tompkins dostal gazetu i popytalsya sosredotochit'sya na poslednih
korrespondenciyah s teatra voennyh dejstvij vo V'etname. No vse soobshcheniya
pokazalis' emu nevynosimo skuchnymi, a zheleznodorozhnyj vagon tak priyatno
pokachivalo...
Kogda Tompkins opustil gazetu i snova vyglyanul v okno, pejzazh sil'no
izmenilsya. Telegrafnye stolby stoyali tak blizko drug ot druga, chto
napominali gigantskuyu izgorod', a krony derev'ev byli takimi uzkimi, chto
derev'ya napominali ital'yanskie kiparisy. Naprotiv mistera Tompkinsa v kupe
sidel ego staryj znakomyj - professor i s zhivejshim interesom smotrel v okno.
Po-vidimomu, on voshel v kupe, poka mister Tompkins byl zanyat chteniem gazety.
- My nahodimsya v strane otnositel'nosti, esli ya ne oshibayus', - zametil
mister Tompkins.
- O! - voskliknul professor. - Ne ozhidal vstretit' poputchika,
obladayushchego stol' glubokimi poznaniyami! A po kakomu uchebniku vy izuchali
teoriyu otnositel'nosti?
- Mne uzhe dovodilos' byvat' zdes', hotya ya ne imel chesti byt' vashim
poputchikom.
- Na etot raz vam pridetsya byt' moim gidom, - skazal staryj professor.
- Boyus', chto mne pridetsya otkazat'sya ot etoj pochetnoj roli, - otklonil
lestnoe predlozhenie mister Tompkins. - YA dejstvitel'no videl mnozhestvo
neobychnyh veshchej, no mestnye zhiteli, k kotorym ya obrashchalsya za raz座asneniyami,
nikak ne mogli vzyat' v tolk, chto menya smushchaet.
- Vpolne estestvenno, - zametil professor. - Ved' oni rodilis' v etom
mire, i vse proishodyashchie vokrug nih yavleniya kazhutsya im samoochevidnymi.
Predstavlyayu, kak oni udivilis' by, esli by im dovelos' pobyvat' v tom mire,
gde privykli zhit' vy. Dumayu, on pokazalsya by im ves'ma neobychnym.
- Pozvol'te zadat' vam odin vopros, - skazal mister Tompkins. - V
proshlyj raz, kogda ya byl zdes', mne vstretilsya tormoznoj konduktor s
zheleznoj dorogi. On utverzhdal, budto iz-za togo, chto poezd ostanavlivaetsya i
trogaetsya v put', passazhiry staryatsya bystree, chem lyudi v gorode. CHto eto -
chudesa ili yavlenie, kotoroe soglasuetsya s sovremennoj naukoj?
- Ssylat'sya na chudesa pri ob座asnenii chego ugodno - priem zapreshchennyj, -
otvetil professor. - YAvlenie, o kotorom govoril vash konduktor, sleduet iz
zakonov fiziki. Analiziruya novye (ili, luchshe skazat', starye, no lish'
nezadolgo do togo otkrytye) ponyatiya prostranstva i vremeni, |jnshtejn
pokazal, chto vse fizicheskie processy zamedlyayutsya, kogda sistema, v kotoroj
oni proishodyat, izmenyaet svoyu skorost'. V nashem mire takie effekty pochti
nezametny, no zdes' iz-za maloj skorosti sveta oni stanovyatsya legko
nablyudaemymi. Naprimer, esli vy popytaetes' zdes' svarit' sebe na zavtrak
yajco i vmesto togo, chtoby dat' kastryul'ke spokojno stoyat' na ogne, nachnete
dvigat' ee to v odnu, to v druguyu storonu, to svarit' yajco vkrutuyu vam
udastsya ne za pyat', a, skazhem, za shest' minut. Vse processy v chelovecheskom
tele takzhe zamedlyayutsya, esli, naprimer, chelovek kachaetsya v kresle-kachalke
ili sidit v kupe poezda, kotoryj zamedlyaet ili uskoryaet hod: v takogo roda
usloviyah my zhivem medlennee. No poskol'ku vse processy zamedlyayutsya
odinakovo, fiziki predpochitayut govorit', chto v _neravnomerno dvizhushchejsya
sisteme vremya techet medlennee_.
- A nablyudayut li takie yavleniya uchenye v nashem mire, tak skazat', u nas
doma?
- Nablyudayut, hotya dlya etogo im prihoditsya proyavlyat' nedyuzhinnoe
eksperimental'noe iskusstvo. Tehnicheski ochen' trudno dostich' neobhodimyh
uskorenij, a fizicheskie usloviya v neravnomerno dvizhushchejsya sisteme
analogichny, ya by dazhe skazal "tozhdestvenny", rezul'tatu vozdejstviya ochen'
bol'shoj sily tyazhesti. Vam, dolzhno byt', prihodilos' zamechat', chto v kabine
podnimayushchegosya s uskoreniem lifta vam kazhetsya, chto vy stanovites' tyazhelee.
Naoborot, esli lift opuskaetsya (naprimer, esli oborvalsya tros i lift
padaet), to vy oshchushchaete kak by poteryu vesa. Ob座asnenie izmenenij vesa
sostoit v tom, chto sozdavaemoe uskoreniem gravitacionnoe pole dobavlyaetsya
ili vychitaetsya iz sily tyazhesti Zemli. Potencial sily tyazhesti na Solnce vo
mnogo raz bol'she, chem na poverhnosti Zemli, i poetomu vse processy na Solnce
nemnogo zamedlyayutsya. Astronomy nablyudayut eto.
- No ved' oni ne mogut otpravit'sya na Solnce, chtoby nablyudat'
zamedlenie vseh processov?
- Im i ne nuzhno tuda otpravlyat'sya. Oni nablyudayut svet, prihodyashchij k nam
ot Solnca. |tot svet porozhdaetsya kolebaniyami razlichnyh atomov v solnechnoj
atmosfere. Esli vse processy na Solnce idut medlennee, to skorost' atomnyh
kolebanij takzhe ubyvaet i, sravnivaya svet, ispuskaemyj Solncem i zemnymi
istochnikami, astronomy mogut zametit' raznicu.
- Kstati, vy ne znaete, kak nazyvaetsya nebol'shaya stanciya, mimo kotoroj
my sejchas proezzhaem? - prerval sebya professor.
Poezd katilsya vdol' perrona malen'koj zaholustnoj stancii. Perron byl
sovershenno pust, esli ne schitat' nachal'nika stancii i molodogo nosil'shchika,
sidevshego na bagazhnoj telezhke i chitavshego gazetu. Vdrug nachal'nik stancii
kak-to nelepo vzmahnul rukami i upal nichkom. Mister Tomkins ne slyshal zvuka
vystrela, dolzhno byt', zaglushennogo stukom koles poezda, no luzha krovi u
tela nachal'nika stancii ne ostavlyala somnenij v tom, chto proizoshlo ubijstvo.
Professor ne medlya dernul stop-kran, i poezd ryvkom ostanovilsya. Kogda
mister Tompkins i professor vyshli iz vagona, nosil'shchik bezhal k telu i na
perrone poyavilsya mestnyj polismen.
- Ubit vystrelom v serdce, - konstatiroval polismen, osmotrev telo, i,
polozhiv tyazheluyu ruku na plecho nosil'shchika, prodolzhil:
- Vy arestovany za ubijstvo nachal'nika stancii.
- Ne ubival ya ego, - zakrichal neschastnyj nosil'shchik. - YA chital gazetu,
kak vdrug uslyshal vystrel. Vozmozhno, eti dzhentl'meny s poezda videli, kak
vse proizoshlo i mogut podtverdit', chto ya ne vinoven.
- Dejstvitel'no, - podtverdil mister Tompkins, - ya videl svoimi
sobstvennymi glazami, kak etot chelovek chital gazetu v tot moment, kogda byl
zastrelen nachal'nik stancii. Mogu poklyast'sya na Biblii.
- No vy nahodilis' v dvizhushchemsya poezde, - zametil polismen, obretaya
nachal'stvennyj ton, - i poetomu vashi pokazaniya ne imeyut dokazatel'noj sily.
S tochki zreniya nablyudatelya na perrone etot chelovek mog byt' zastrelen v tot
zhe samyj moment. Razve vy ne znaete, chto odnovremennost' sobytij zavisit ot
sistemy otscheta, iz kotoroj vy ee nablyudaete? Projdem bez lishnego shuma, -
obratilsya on k nosil'shchiku.
- Proshu izvinit' menya, konstebl', - prerval ego professor, - no vy
sovershenno ne pravy i ya ne dumayu, chto v policejskom upravlenii ochen'
obraduyutsya, uznav o vashem nevezhestve. Nikto ne sporit: v vashej strane
ponyatie odnovremennosti v vysshej stepeni otnositel'no. |to pravda. Verno i
to, chto dva sobytiya, proishodyashchih v razlichnyh mestah, mogut byt'
odnovremennymi ili ne odnovremennymi v zavisimosti ot dvizheniya nablyudatelya.
No dazhe v vashej strane ni odin nablyudatel' ne mozhet videt' sledstvie ran'she,
chem prichinu. Vam zhe nikogda ne sluchalos' poluchat' telegrammu do togo, kak ta
byla otpravlena, ved' verno? Ne sluchalos' i pit' do togo, kak butylku
otkuporili. Naskol'ko ya vas ponimayu, vy polagaete, chto iz-za dvizheniya poezda
my, passazhiry, nablyudali vystrel gorazdo _pozzhe_, chem ego sledstvie,
poskol'ku, vyskochiv iz vagona totchas zhe posle ekstrennoj ostanovki poezda,
my uvideli nachal'nika stancii lezhashchim na zemle, no eshche ne videli samogo
vystrela. YA znayu, chto v policii vas uchat verit' tol'ko tomu, chto napisano v
vashih instrukciyah. Vzglyanite v nih i vy, veroyatno, otyshchite chto-nibud'
podhodyashchee k sluchayu.
Ton professora proizvel neizgladimoe vpechatlenie na polismena i,
vytashchiv karmannyj svod instrukcij, on prinyalsya medlenno, stranica za
stranicej izuchat' ih. Vskore po ego shirokoj krasnoj fizionomii razlilas'
ulybka oblegcheniya.
- Vot, - skazal on, - razdel 37, chast' 12, paragraf e: "V kachestve
absolyutno nadezhnogo alibi sleduet schitat' lyuboe avtoritetnoe dokazatel'stvo
togo, chto iz lyuboj dvizhushchejsya sistemy otscheta v moment soversheniya
prestupleniya ili v techenie intervala vremeni +-cd (gde s - skorost' sveta, a
d - rasstoyanie ot mesta prestupleniya) podozrevaemogo videli v drugom meste".
- Vy svobodny, moj milyj, - obratilsya polismen k nosil'shchiku i dobavil,
povernuvshis' k professoru:
- Ochen' priznatelen vam, ser, chto vy izbavili menya ot nepriyatnostej s
policejskim upravleniem. YA v policii sluzhu nedavno i eshche ne vyuchil nazubok
vse pravila. No mne vse ravno neobhodimo dolozhit' ob ubijstve. I polismen
pospeshil k telefonnoj budke. CHerez minutu on zakrichal na ves' perron:
- Vse v poryadke! Oni pojmali nastoyashchego ubijcu, kogda tot bezhal so
stancii. Eshche raz blagodaryu vas, ser!
- Dolzhno byt', ya neprohodimo glup, - zametil mister Tompkins, kogda
poezd snova tronulsya, - no chto oznachaet vsya eta nerazberiha s
odnovremennost'yu? Imeet li odnovremennost' voobshche kakoj-nibud' smysl v etoj
strane?
- Imeet, - glasil otvet professora, - no lish' v opredelennoj stepeni,
inache ya ne smog by pomoch' bednyage-nosil'shchiku. Delo v tom, chto esli
sushchestvuet estestvennyj predel skorosti dlya dvizheniya lyubogo tela ili
rasprostraneniya lyubogo signala, to odnovremennost' v obychnom smysle etogo
slova utrachivaet smysl. Vam, veroyatno, budet legche ponyat' sut' dela na
sleduyushchem primere. Predpolozhim, chto u vas est' drug, zhivushchij v dalekom
gorode, s kotorym vy perepisyvaetes', i pochtovyj poezd, kotoryj otpravlyaetsya
raz v sutki, - samoe bystroe sredstvo soobshcheniya. Predpolozhim teper', chto
kakoe-to proisshestvie sluchilos' s vami v voskresen'e i vy uznali, chto
analogichnoe proisshestvie dolzhno proizojti s vashim drugom. YAsno, chto vy ne
mozhete uvedomit' ego ob etom ran'she vtornika. S drugoj storony, esli by on
znal zaranee o tom, chto proizojdet s vami, to poslednij den', kogda on mog
predupredit' vas o gryadushchem sobytii, byl chetverg na proshloj nedele. Takim
obrazom, v techenie shesti dnej - s chetverga na proshloj nedele do vtornika na
budushchej nedele - vash drug ne sposoben ni povliyat' na vashu sud'bu v
voskresen'e, ni uznat' o tom, chto s vami proizoshlo. S tochki zreniya
prichinnosti on iz座at iz obshcheniya s vami, ili, tak skazat', ekskommunicirovan.
- A chto esli emu poslat' telegrammu? - predlozhil mister Tompkins.
- No ved' ya predpolozhil, chto skorost' pochtovogo poezda - maksimal'no
vozmozhnaya. Primerno tak i obstoit delo v etoj strane. U nas na rodine
maksimal'noj skorost'yu yavlyaetsya skorost' sveta, i vy ne mozhete poslat'
signal, kotoroj rasprostranyalsya by bystree, chem radiosignal.
- Pust' tak, - soglasilsya mister Tompkins, - no dazhe esli nichto ne
mozhet prevzojti skorost' pochtovogo poezda, ya vse ravno ne ponimayu, kakoe eto
imeet otnoshenie k odnovremennosti. Moj drug i ya po-prezhnemu obedaem po
voskresen'yam v odno i to zhe vremya. Razve ne tak?
- Net, ne tak. Vashe utverzhdenie voobshche ne imelo by smysla: odin
nablyudatel' soglasilsya by s tem, chto vy s priyatelem obedaete odnovremenno, a
drugie nablyudateli, proizvodivshie svoi nablyudeniya iz drugih poezdov,
utverzhdali by, chto vy obedaete po voskresen'yam v to samoe vremya, kogda vash
drug zavtrakaet po pyatnicam ili uzhinaet po vtornikam. No nikto ne mozhet
nablyudat' vas i vashego druga za odnovremennoj trapezoj, esli vas razdelyaet
vremennoj interval bolee treh dnej.
- No kak eto mozhet byt'? - voskliknul nedoverchivo mister Tompkins.
- Proishodit vse eto tochno tak, kak vy, vozmozhno, uyasnili sebe iz moih
lekcij. Verhnij predel skorosti dolzhen ostavat'sya odnim i tem zhe pri
nablyudenii iz razlichnyh dvizhushchihsya sistem otscheta. Prinyav takoe
predpolozhenie, my s neobhodimost'yu prihodim k zaklyucheniyu o tom, chto...
Tut razgovor, k sozhaleniyu, prervalsya, tak kak poezd pribyl na tu
stanciyu, gde misteru Tompkinsu nuzhno bylo shodit'.
Kogda mister Tompkins spustilsya k zavtraku na dlinnuyu zasteklennuyu
verandu otelya na sleduyushchee utro posle svoego pribytiya na poberezh'e, ego
ozhidal priyatnyj syurpriz: na protivopolozhnom konce stola protiv nego vossedal
staryj professor s krasivoj molodoj devushkoj, kotoraya ozhivlenno chto-to
govorila emu, chasto poglyadyvaya v tu storonu, gde sidel mister Tompkins.
- Dolzhno byt', ya sovershil bol'shuyu glupost', kogda zasnul v poezde, -
podumal mister Tompkins, serdyas' na sebya vse bol'she i bol'she, - a professor
vse eshche pomnit tot glupyj vopros, kotoryj ya zadal emu o molodeyushchih
passazhirah. No po krajnej mere eto pozvolyaet mne prodolzhit' znakomstvo s
professorom i rassprosit' ego o tom, chto mne po-prezhnemu neponyatno.
Dazhe samomu sebe mister Tompkins ne hotel priznat'sya, chto dumaet ne
tol'ko o professore, no i o ego horoshen'koj sputnice.
- Da, da, konechno, ya pomnyu, chto videl vas na svoih lekciyah, - skazal
professor, kogda oni vyhodili iz obedennogo zala. - Poznakom'tes', eto moya
doch' Mod. Ona zanimaetsya zhivopis'yu.
- Rad poznakomit'sya s vami, miss Mod, - otvetil mister Tompkins i
podumal, chto nikogda ne slyshal bolee krasivogo imeni. - Dumayu, chto zdeshnie
krasoty dadut vam nemalo materiala dlya vashih etyudov.
- Mod nepremenno pokazhet ih vam kogda-nibud', - poobeshchal professor. - A
sejchas skazhite mne luchshe, mnogo li vy pocherpnuli iz moej lekcii?
- O da, ochen' mnogo! Bolee togo, ya na sebe prochuvstvoval vse eti
relyativistskie sokrashcheniya material'nyh ob容ktov i sumasshedshee povedenie
chasov, kogda pobyval v gorode, gde skorost' sveta sostavlyala tol'ko
kilometrov desyat' v chas.
- ZHal', chto vy propustili moyu sleduyushchuyu lekciyu o krivizne prostranstva
i ee svyazi s silami n'yutonovskoj gravitacii, - zadumchivo proiznes professor.
- No zdes', na poberezh'e, u nas hvatit vremeni, i ya nadeyus' ob座asnit' vam
vse eto. Naprimer, ponimaete li vy, v chem raznica mezhdu polozhitel'noj i
otricatel'noj kriviznoj prostranstva?
- Papochka, - vmeshalas' miss Mod, kaprizno naduv guby, - esli vy
sobiraetes' snova besedovat' o fizike, to ya luchshe zajmus' etyudami.
- Horosho, devochka, idi, - soglasilsya professor, opuskayas' v legkoe
kreslo. - YA vizhu, chto vy molodoj chelovek, ne ochen' svedushchi v matematike, no
dumayu, chto udastsya ob座asnit' vam vse ochen' prosto. Dlya bol'shej naglyadnosti ya
budu govorit' o poverhnosti. Predstav'te sebe, chto mister SHell (vy znaete, o
kom ya govoryu, - eto tot samyj gospodin, kotoryj vladeet benzozapravochnymi
stanciyami "SHell Ojl") reshil kak-to raz prosledit' za tem, chtoby ego
zapravochnye stancii byli ravnomerno raspredeleny po territorii kakoj-nibud'
strany, naprimer, Ameriki. Dlya etogo mister SHell otdal pravleniyu svoej
firmy, raspolozhennomu gde-to v centre strany (esli ya ne oshibayus', mnogie
sklonny dumat', chto serdce Ameriki nahoditsya v Kanzas-Siti), rasporyazhenie
soschitat' chislo stancij na rasstoyanii sto, dvesti, trista i t. d. mil' ot
centra. So shkol'noj skam'i mister SHell vynes vospominaniya o tom, chto ploshchad'
kruga proporcional'na kvadratu ego radiusa, i ozhidaet, chto v sluchae
ravnomernogo raspredeleniya zapravochnyh stancij chislo ih v rezul'tate
podschetov budet vozrastat', kak posledovatel'nost' chisel 1; 4; 9; 16 i t.d.
Kogda v pravlenie "SHell Ojl" stali postupat' otchety, glava firmy k svoemu
velikomu udivleniyu obnaruzhil, chto chislo stancij vozrastaet gorazdo
medlennee, naprimer, kak chisla, obrazuyushchie posledovatel'nost' 1; 3,8; 8,5;
15,0 i t.d.
(4)
My vidim, chto soprotivlenie tela dal'nejshemu uskoreniyu stanovitsya
beskonechno bol'shim, kogda i stremitsya k c. |tot effekt relyativistskogo
izmeneniya massy mozhet byt' legko nablyudaem eksperimental'no na chasticah,
dvizhushchihsya s ochen' bol'shimi skorostyami. Naprimer, massa elektronov,
ispuskaemyh radioaktivnymi telami (so skorost'yu, sostavlyayushchej 99 % skorosti
sveta), v neskol'ko raz bol'she, chem v sostoyanii pokoya, a massy elektronov,
obrazuyushchih tak nazyvaemye kosmicheskie livni i neredko dvizhushchihsya so
skorost'yu 99,98 % skorosti sveta, v 1000 raz bol'she. K takim skorostyam
klassicheskaya mehanika stanovitsya absolyutno neprimenimoj, i my vstupaem v
oblast' chistoj teorii otnositel'nosti.
Mister Tompkins beret otpusk
Misteru Tompkinsu ochen' ponravilis' priklyucheniya v relyativistskom
gorode, ogorchalo tol'ko, chto s nim ne bylo professora, kotoryj mog by
ob座asnit' neobychnye yavleniya, kotorye emu, misteru Tompkinsu, dovelos' tam
nablyudat', naprimer, pomoch' razreshit' zagadku, osobenno zanimavshuyu ego:
kakim obrazom tormoznomu konduktoru udavalos' predupredit' starenie
passazhirov? Mnogo nochej podryad mister Tompkins ukladyvalsya v postel' s
nadezhdoj snova uvidet' polyubivshijsya emu gorod, no sny mister Tompkins videl
redko i, v osnovnom, dovol'no nepriyatnye. Naprimer, v poslednij raz misteru
Tompkinsu prisnilos', chto upravlyayushchij bankom uvolil ego za nebrezhnost' v
vedenii bankovskih schetov. Prosnuvshis', mister Tompkins schel za blago vzyat'
otpusk i otpravit'sya na nedel'ku kuda-nibud' na more. Tak mister Tompkins
okazalsya v kupe poezda, nablyudaya v okno, kak serye kryshi prigoroda
postepenno ustupayut mesto zelenym luzhajkam sel'skoj mestnosti. Mister
Tompkins dostal gazetu i popytalsya sosredotochit'sya na poslednih
korrespondenciyah s teatra voennyh dejstvij vo V'etname. No vse soobshcheniya
pokazalis' emu nevynosimo skuchnymi, a zheleznodorozhnyj vagon tak priyatno
pokachivalo...
Kogda Tompkins opustil gazetu i snova vyglyanul v okno, pejzazh sil'no
izmenilsya. Telegrafnye stolby stoyali tak blizko drug ot druga, chto
napominali gigantskuyu izgorod', a krony derev'ev byli takimi uzkimi, chto
derev'ya napominali ital'yanskie kiparisy. Naprotiv mistera Tompkinsa v kupe
sidel ego staryj znakomyj - professor i s zhivejshim interesom smotrel v okno.
Po-vidimomu, on voshel v kupe, poka mister Tompkins byl zanyat chteniem gazety.
- My nahodimsya v strane otnositel'nosti, esli ya ne oshibayus', - zametil
mister Tompkins.
- O! - voskliknul professor. - Ne ozhidal vstretit' poputchika,
obladayushchego stol' glubokimi poznaniyami! A po kakomu uchebniku vy izuchali
teoriyu otnositel'nosti?
- Mne uzhe dovodilos' byvat' zdes', hotya ya ne imel chesti byt' vashim
poputchikom.
- Na etot raz vam pridetsya byt' moim gidom, - skazal staryj professor.
- Boyus', chto mne pridetsya otkazat'sya ot etoj pochetnoj roli, - otklonil
lestnoe predlozhenie mister Tompkins. - YA dejstvitel'no videl mnozhestvo
neobychnyh veshchej, no mestnye zhiteli, k kotorym ya obrashchalsya za raz座asneniyami,
nikak ne mogli vzyat' v tolk, chto menya smushchaet.
- Vpolne estestvenno, - zametil professor. - Ved' oni rodilis' v etom
mire, i vse proishodyashchie vokrug nih yavleniya kazhutsya im samoochevidnymi.
Predstavlyayu, kak oni udivilis' by, esli by im dovelos' pobyvat' v tom mire,
gde privykli zhit' vy. Dumayu, on pokazalsya by im ves'ma neobychnym.
- Pozvol'te zadat' vam odin vopros, - skazal mister Tompkins. - V
proshlyj raz, kogda ya byl zdes', mne vstretilsya tormoznoj konduktor s
zheleznoj dorogi. On utverzhdal, budto iz-za togo, chto poezd ostanavlivaetsya i
trogaetsya v put', passazhiry staryatsya bystree, chem lyudi v gorode. CHto eto -
chudesa ili yavlenie, kotoroe soglasuetsya s sovremennoj naukoj?
- Ssylat'sya na chudesa pri ob座asnenii chego ugodno - priem zapreshchennyj, -
otvetil professor. - YAvlenie, o kotorom govoril vash konduktor, sleduet iz
zakonov fiziki. Analiziruya novye (ili, luchshe skazat', starye, no lish'
nezadolgo do togo otkrytye) ponyatiya prostranstva i vremeni, |jnshtejn
pokazal, chto vse fizicheskie processy zamedlyayutsya, kogda sistema, v kotoroj
oni proishodyat, izmenyaet svoyu skorost'. V nashem mire takie effekty pochti
nezametny, no zdes' iz-za maloj skorosti sveta oni stanovyatsya legko
nablyudaemymi. Naprimer, esli vy popytaetes' zdes' svarit' sebe na zavtrak
yajco i vmesto togo, chtoby dat' kastryul'ke spokojno stoyat' na ogne, nachnete
dvigat' ee to v odnu, to v druguyu storonu, to svarit' yajco vkrutuyu vam
udastsya ne za pyat', a, skazhem, za shest' minut. Vse processy v chelovecheskom
tele takzhe zamedlyayutsya, esli, naprimer, chelovek kachaetsya v kresle-kachalke
ili sidit v kupe poezda, kotoryj zamedlyaet ili uskoryaet hod: v takogo roda
usloviyah my zhivem medlennee. No poskol'ku vse processy zamedlyayutsya
odinakovo, fiziki predpochitayut govorit', chto v _neravnomerno dvizhushchejsya
sisteme vremya techet medlennee_.
- A nablyudayut li takie yavleniya uchenye v nashem mire, tak skazat', u nas
doma?
- Nablyudayut, hotya dlya etogo im prihoditsya proyavlyat' nedyuzhinnoe
eksperimental'noe iskusstvo. Tehnicheski ochen' trudno dostich' neobhodimyh
uskorenij, a fizicheskie usloviya v neravnomerno dvizhushchejsya sisteme
analogichny, ya by dazhe skazal "tozhdestvenny", rezul'tatu vozdejstviya ochen'
bol'shoj sily tyazhesti. Vam, dolzhno byt', prihodilos' zamechat', chto v kabine
podnimayushchegosya s uskoreniem lifta vam kazhetsya, chto vy stanovites' tyazhelee.
Naoborot, esli lift opuskaetsya (naprimer, esli oborvalsya tros i lift
padaet), to vy oshchushchaete kak by poteryu vesa. Ob座asnenie izmenenij vesa
sostoit v tom, chto sozdavaemoe uskoreniem gravitacionnoe pole dobavlyaetsya
ili vychitaetsya iz sily tyazhesti Zemli. Potencial sily tyazhesti na Solnce vo
mnogo raz bol'she, chem na poverhnosti Zemli, i poetomu vse processy na Solnce
nemnogo zamedlyayutsya. Astronomy nablyudayut eto.
- No ved' oni ne mogut otpravit'sya na Solnce, chtoby nablyudat'
zamedlenie vseh processov?
- Im i ne nuzhno tuda otpravlyat'sya. Oni nablyudayut svet, prihodyashchij k nam
ot Solnca. |tot svet porozhdaetsya kolebaniyami razlichnyh atomov v solnechnoj
atmosfere. Esli vse processy na Solnce idut medlennee, to skorost' atomnyh
kolebanij takzhe ubyvaet i, sravnivaya svet, ispuskaemyj Solncem i zemnymi
istochnikami, astronomy mogut zametit' raznicu.
- Kstati, vy ne znaete, kak nazyvaetsya nebol'shaya stanciya, mimo kotoroj
my sejchas proezzhaem? - prerval sebya professor.
Poezd katilsya vdol' perrona malen'koj zaholustnoj stancii. Perron byl
sovershenno pust, esli ne schitat' nachal'nika stancii i molodogo nosil'shchika,
sidevshego na bagazhnoj telezhke i chitavshego gazetu. Vdrug nachal'nik stancii
kak-to nelepo vzmahnul rukami i upal nichkom. Mister Tomkins ne slyshal zvuka
vystrela, dolzhno byt', zaglushennogo stukom koles poezda, no luzha krovi u
tela nachal'nika stancii ne ostavlyala somnenij v tom, chto proizoshlo ubijstvo.
Professor ne medlya dernul stop-kran, i poezd ryvkom ostanovilsya. Kogda
mister Tompkins i professor vyshli iz vagona, nosil'shchik bezhal k telu i na
perrone poyavilsya mestnyj polismen.
- Ubit vystrelom v serdce, - konstatiroval polismen, osmotrev telo, i,
polozhiv tyazheluyu ruku na plecho nosil'shchika, prodolzhil:
- Vy arestovany za ubijstvo nachal'nika stancii.
- Ne ubival ya ego, - zakrichal neschastnyj nosil'shchik. - YA chital gazetu,
kak vdrug uslyshal vystrel. Vozmozhno, eti dzhentl'meny s poezda videli, kak
vse proizoshlo i mogut podtverdit', chto ya ne vinoven.
- Dejstvitel'no, - podtverdil mister Tompkins, - ya videl svoimi
sobstvennymi glazami, kak etot chelovek chital gazetu v tot moment, kogda byl
zastrelen nachal'nik stancii. Mogu poklyast'sya na Biblii.
- No vy nahodilis' v dvizhushchemsya poezde, - zametil polismen, obretaya
nachal'stvennyj ton, - i poetomu vashi pokazaniya ne imeyut dokazatel'noj sily.
S tochki zreniya nablyudatelya na perrone etot chelovek mog byt' zastrelen v tot
zhe samyj moment. Razve vy ne znaete, chto odnovremennost' sobytij zavisit ot
sistemy otscheta, iz kotoroj vy ee nablyudaete? Projdem bez lishnego shuma, -
obratilsya on k nosil'shchiku.
- Proshu izvinit' menya, konstebl', - prerval ego professor, - no vy
sovershenno ne pravy i ya ne dumayu, chto v policejskom upravlenii ochen'
obraduyutsya, uznav o vashem nevezhestve. Nikto ne sporit: v vashej strane
ponyatie odnovremennosti v vysshej stepeni otnositel'no. |to pravda. Verno i
to, chto dva sobytiya, proishodyashchih v razlichnyh mestah, mogut byt'
odnovremennymi ili ne odnovremennymi v zavisimosti ot dvizheniya nablyudatelya.
No dazhe v vashej strane ni odin nablyudatel' ne mozhet videt' sledstvie ran'she,
chem prichinu. Vam zhe nikogda ne sluchalos' poluchat' telegrammu do togo, kak ta
byla otpravlena, ved' verno? Ne sluchalos' i pit' do togo, kak butylku
otkuporili. Naskol'ko ya vas ponimayu, vy polagaete, chto iz-za dvizheniya poezda
my, passazhiry, nablyudali vystrel gorazdo _pozzhe_, chem ego sledstvie,
poskol'ku, vyskochiv iz vagona totchas zhe posle ekstrennoj ostanovki poezda,
my uvideli nachal'nika stancii lezhashchim na zemle, no eshche ne videli samogo
vystrela. YA znayu, chto v policii vas uchat verit' tol'ko tomu, chto napisano v
vashih instrukciyah. Vzglyanite v nih i vy, veroyatno, otyshchite chto-nibud'
podhodyashchee k sluchayu.
Ton professora proizvel neizgladimoe vpechatlenie na polismena i,
vytashchiv karmannyj svod instrukcij, on prinyalsya medlenno, stranica za
stranicej izuchat' ih. Vskore po ego shirokoj krasnoj fizionomii razlilas'
ulybka oblegcheniya.
- Vot, - skazal on, - razdel 37, chast' 12, paragraf e: "V kachestve
absolyutno nadezhnogo alibi sleduet schitat' lyuboe avtoritetnoe dokazatel'stvo
togo, chto iz lyuboj dvizhushchejsya sistemy otscheta v moment soversheniya
prestupleniya ili v techenie intervala vremeni +-cd (gde s - skorost' sveta, a
d - rasstoyanie ot mesta prestupleniya) podozrevaemogo videli v drugom meste".
- Vy svobodny, moj milyj, - obratilsya polismen k nosil'shchiku i dobavil,
povernuvshis' k professoru:
- Ochen' priznatelen vam, ser, chto vy izbavili menya ot nepriyatnostej s
policejskim upravleniem. YA v policii sluzhu nedavno i eshche ne vyuchil nazubok
vse pravila. No mne vse ravno neobhodimo dolozhit' ob ubijstve. I polismen
pospeshil k telefonnoj budke. CHerez minutu on zakrichal na ves' perron:
- Vse v poryadke! Oni pojmali nastoyashchego ubijcu, kogda tot bezhal so
stancii. Eshche raz blagodaryu vas, ser!
- Dolzhno byt', ya neprohodimo glup, - zametil mister Tompkins, kogda
poezd snova tronulsya, - no chto oznachaet vsya eta nerazberiha s
odnovremennost'yu? Imeet li odnovremennost' voobshche kakoj-nibud' smysl v etoj
strane?
- Imeet, - glasil otvet professora, - no lish' v opredelennoj stepeni,
inache ya ne smog by pomoch' bednyage-nosil'shchiku. Delo v tom, chto esli
sushchestvuet estestvennyj predel skorosti dlya dvizheniya lyubogo tela ili
rasprostraneniya lyubogo signala, to odnovremennost' v obychnom smysle etogo
slova utrachivaet smysl. Vam, veroyatno, budet legche ponyat' sut' dela na
sleduyushchem primere. Predpolozhim, chto u vas est' drug, zhivushchij v dalekom
gorode, s kotorym vy perepisyvaetes', i pochtovyj poezd, kotoryj otpravlyaetsya
raz v sutki, - samoe bystroe sredstvo soobshcheniya. Predpolozhim teper', chto
kakoe-to proisshestvie sluchilos' s vami v voskresen'e i vy uznali, chto
analogichnoe proisshestvie dolzhno proizojti s vashim drugom. YAsno, chto vy ne
mozhete uvedomit' ego ob etom ran'she vtornika. S drugoj storony, esli by on
znal zaranee o tom, chto proizojdet s vami, to poslednij den', kogda on mog
predupredit' vas o gryadushchem sobytii, byl chetverg na proshloj nedele. Takim
obrazom, v techenie shesti dnej - s chetverga na proshloj nedele do vtornika na
budushchej nedele - vash drug ne sposoben ni povliyat' na vashu sud'bu v
voskresen'e, ni uznat' o tom, chto s vami proizoshlo. S tochki zreniya
prichinnosti on iz座at iz obshcheniya s vami, ili, tak skazat', ekskommunicirovan.
- A chto esli emu poslat' telegrammu? - predlozhil mister Tompkins.
- No ved' ya predpolozhil, chto skorost' pochtovogo poezda - maksimal'no
vozmozhnaya. Primerno tak i obstoit delo v etoj strane. U nas na rodine
maksimal'noj skorost'yu yavlyaetsya skorost' sveta, i vy ne mozhete poslat'
signal, kotoroj rasprostranyalsya by bystree, chem radiosignal.
- Pust' tak, - soglasilsya mister Tompkins, - no dazhe esli nichto ne
mozhet prevzojti skorost' pochtovogo poezda, ya vse ravno ne ponimayu, kakoe eto
imeet otnoshenie k odnovremennosti. Moj drug i ya po-prezhnemu obedaem po
voskresen'yam v odno i to zhe vremya. Razve ne tak?
- Net, ne tak. Vashe utverzhdenie voobshche ne imelo by smysla: odin
nablyudatel' soglasilsya by s tem, chto vy s priyatelem obedaete odnovremenno, a
drugie nablyudateli, proizvodivshie svoi nablyudeniya iz drugih poezdov,
utverzhdali by, chto vy obedaete po voskresen'yam v to samoe vremya, kogda vash
drug zavtrakaet po pyatnicam ili uzhinaet po vtornikam. No nikto ne mozhet
nablyudat' vas i vashego druga za odnovremennoj trapezoj, esli vas razdelyaet
vremennoj interval bolee treh dnej.
- No kak eto mozhet byt'? - voskliknul nedoverchivo mister Tompkins.
- Proishodit vse eto tochno tak, kak vy, vozmozhno, uyasnili sebe iz moih
lekcij. Verhnij predel skorosti dolzhen ostavat'sya odnim i tem zhe pri
nablyudenii iz razlichnyh dvizhushchihsya sistem otscheta. Prinyav takoe
predpolozhenie, my s neobhodimost'yu prihodim k zaklyucheniyu o tom, chto...
Tut razgovor, k sozhaleniyu, prervalsya, tak kak poezd pribyl na tu
stanciyu, gde misteru Tompkinsu nuzhno bylo shodit'.
Kogda mister Tompkins spustilsya k zavtraku na dlinnuyu zasteklennuyu
verandu otelya na sleduyushchee utro posle svoego pribytiya na poberezh'e, ego
ozhidal priyatnyj syurpriz: na protivopolozhnom konce stola protiv nego vossedal
staryj professor s krasivoj molodoj devushkoj, kotoraya ozhivlenno chto-to
govorila emu, chasto poglyadyvaya v tu storonu, gde sidel mister Tompkins.
- Dolzhno byt', ya sovershil bol'shuyu glupost', kogda zasnul v poezde, -
podumal mister Tompkins, serdyas' na sebya vse bol'she i bol'she, - a professor
vse eshche pomnit tot glupyj vopros, kotoryj ya zadal emu o molodeyushchih
passazhirah. No po krajnej mere eto pozvolyaet mne prodolzhit' znakomstvo s
professorom i rassprosit' ego o tom, chto mne po-prezhnemu neponyatno.
Dazhe samomu sebe mister Tompkins ne hotel priznat'sya, chto dumaet ne
tol'ko o professore, no i o ego horoshen'koj sputnice.
- Da, da, konechno, ya pomnyu, chto videl vas na svoih lekciyah, - skazal
professor, kogda oni vyhodili iz obedennogo zala. - Poznakom'tes', eto moya
doch' Mod. Ona zanimaetsya zhivopis'yu.
- Rad poznakomit'sya s vami, miss Mod, - otvetil mister Tompkins i
podumal, chto nikogda ne slyshal bolee krasivogo imeni. - Dumayu, chto zdeshnie
krasoty dadut vam nemalo materiala dlya vashih etyudov.
- Mod nepremenno pokazhet ih vam kogda-nibud', - poobeshchal professor. - A
sejchas skazhite mne luchshe, mnogo li vy pocherpnuli iz moej lekcii?
- O da, ochen' mnogo! Bolee togo, ya na sebe prochuvstvoval vse eti
relyativistskie sokrashcheniya material'nyh ob容ktov i sumasshedshee povedenie
chasov, kogda pobyval v gorode, gde skorost' sveta sostavlyala tol'ko
kilometrov desyat' v chas.
- ZHal', chto vy propustili moyu sleduyushchuyu lekciyu o krivizne prostranstva
i ee svyazi s silami n'yutonovskoj gravitacii, - zadumchivo proiznes professor.
- No zdes', na poberezh'e, u nas hvatit vremeni, i ya nadeyus' ob座asnit' vam
vse eto. Naprimer, ponimaete li vy, v chem raznica mezhdu polozhitel'noj i
otricatel'noj kriviznoj prostranstva?
- Papochka, - vmeshalas' miss Mod, kaprizno naduv guby, - esli vy
sobiraetes' snova besedovat' o fizike, to ya luchshe zajmus' etyudami.
- Horosho, devochka, idi, - soglasilsya professor, opuskayas' v legkoe
kreslo. - YA vizhu, chto vy molodoj chelovek, ne ochen' svedushchi v matematike, no
dumayu, chto udastsya ob座asnit' vam vse ochen' prosto. Dlya bol'shej naglyadnosti ya
budu govorit' o poverhnosti. Predstav'te sebe, chto mister SHell (vy znaete, o
kom ya govoryu, - eto tot samyj gospodin, kotoryj vladeet benzozapravochnymi
stanciyami "SHell Ojl") reshil kak-to raz prosledit' za tem, chtoby ego
zapravochnye stancii byli ravnomerno raspredeleny po territorii kakoj-nibud'
strany, naprimer, Ameriki. Dlya etogo mister SHell otdal pravleniyu svoej
firmy, raspolozhennomu gde-to v centre strany (esli ya ne oshibayus', mnogie
sklonny dumat', chto serdce Ameriki nahoditsya v Kanzas-Siti), rasporyazhenie
soschitat' chislo stancij na rasstoyanii sto, dvesti, trista i t. d. mil' ot
centra. So shkol'noj skam'i mister SHell vynes vospominaniya o tom, chto ploshchad'
kruga proporcional'na kvadratu ego radiusa, i ozhidaet, chto v sluchae
ravnomernogo raspredeleniya zapravochnyh stancij chislo ih v rezul'tate
podschetov budet vozrastat', kak posledovatel'nost' chisel 1; 4; 9; 16 i t.d.
Kogda v pravlenie "SHell Ojl" stali postupat' otchety, glava firmy k svoemu
velikomu udivleniyu obnaruzhil, chto chislo stancij vozrastaet gorazdo
medlennee, naprimer, kak chisla, obrazuyushchie posledovatel'nost' 1; 3,8; 8,5;
15,0 i t.d.
 - CHto za d'yavol'shchina, - voskliknul mister SHell, - moi upravlyayushchie v
Amerike nichego ne smyslyat v svoem dele! Nu skazhite na milost', zachem im
ponadobilos' sosredotachivat' zapravochnye stancii v okrestnostyah Kanzas-Siti?
Prav li mister SHell v svoem zaklyuchenii?
- V samom dele, prav li on? - povtoril mister Tompkins, mysli kotorogo
gde-to vitali.
- Mister SHell gluboko zabluzhdaetsya, - mrachno izrek professor. - On
upustil iz vidu, chto poverhnost' Zemli ne ploskaya, a sfericheskaya, a na sfere
ploshchad', zaklyuchennaya vnutri kruga dannogo radiusa, rastet medlennee, chem na
ploskosti. Mozhete vy predstavit' sebe eto naglyadno? Net? Togda voz'mite
globus i ubedites' sami v tom, chto ya prav. Naprimer, esli vy nahodites' na
Severnom polyuse, to okruzhnost' radiusom v polovinu meridiana est' ne chto
inoe, kak ekvator, a zaklyuchennaya vnutri nee ploshchad' poverhnosti Zemli est'
ploshchad' severnogo polushariya. S uvelicheniem radiusa ploshchad' na poverhnosti
sfery vozrastaet tol'ko vdvoe, a ne vchetvero, kak bylo by na ploskosti.
Teper', nadeyus', yasno?
- O, da, - kivnul mister Tompkins, delaya vid, budto on vnimatel'no
sledit za ob座asneniyami. - A chto takoe polozhitel'naya ili otricatel'naya
krivizna?
- U sfery krivizna schitaetsya polozhitel'noj. Kak vy videli na primere
zemnogo shara, polozhitel'naya krivizna sootvetstvuet konechnoj poverhnosti,
imeyushchej konechnuyu ploshchad'. Primerom poverhnosti s otricatel'noj kriviznoj
mozhet sluzhit' sedlo.
- Sedlo? - peresprosil mister Tompkins.
- Da, sedlo, ili na poverhnosti Zemli sedloobraznyj pereval mezhdu dvumya
gornymi vershinami. Predpolozhim, chto nekij botanik obitaet v gornoj hizhine,
raspolozhennoj na takom sedlovidnom perevale, i zanimaetsya izucheniem
plotnosti sosen, rastushchih vokrug ego zhilishcha. Podschitav chislo sosen, rastushchih
ne dalee sta, dvuhsot, trehsot i t. d. futov ot hizhiny, on obnaruzhit, chto
chislo sosen vozrastaet bystree, chem kvadrat rasstoyaniya, poskol'ku na
sedlovidnoj poverhnosti ploshchad', zaklyuchennaya vnutri dannogo radiusa, rastet
bystree, chem na ploskosti. O takih poverhnostyah govoryat, chto oni obladayut
otricatel'noj kriviznoj. Esli vy popytaetes', rastyanuv, nalozhit' sedlovidnuyu
poverhnost' na ploskost', to vam pridetsya sdelat' skladki. Esli zhe vy
zadumaete nalozhit' na ploskost' sfericheskuyu poverhnost', to vam pridetsya
gde-to prodelat' v nej dyrochku.
- Kazhetsya, ya nachinayu ponimat', - zadumchivo proiznes mister Tompkins. -
Vy hotite skazat', chto sedlovidnaya poverhnost' beskonechnaya, hotya i
iskrivlennaya.
- Vot imenno! - odobritel'no kivnul professor. - Sedlovidnaya
poverhnost' prostiraetsya vo vse storony do beskonechnosti i nigde ne
zamykaetsya. Razumeetsya, v moem primere s sedlovidnym perevalom poverhnost'
perestaet byt' poverhnost'yu otricatel'noj krivizny, kak tol'ko vy
spuskaetes' s gor, i perehodit v iskrivlennuyu poverhnost' zemnogo shara s
polozhitel'noj kriviznoj. No, razumeetsya, nichto ne meshaet vam voobrazit'
poverhnost', sohranyayushchuyu povsyudu otricatel'nuyu kriviznu.
- No kakoe otnoshenie imeet vse eto k iskrivlennomu trehmernomu
prostranstvu?
- Samoe neposredstvennoe. Predstav'te sebe, chto kakie-to vashi ob容kty
ravnomerno raspredeleny po vsemu prostranstvu. Pod ravnomernym ya ponimayu
takoe raspredelenie, pri kotorom rasstoyanie mezhdu lyubymi sosednimi ob容ktami
vsegda odno i to zhe. Predpolozhim, chto vy podschityvaete chislo ob容ktov,
raspolozhennyh ne dalee togo ili inogo rasstoyaniya ot vas. Esli eto chislo
rastet kak kvadrat rasstoyaniya, to prostranstvo ploskoe. Esli zhe chislo
ob容ktov rastet medlennee ili bystree, to prostranstvo obladaet
sootvetstvenno polozhitel'noj ili otricatel'noj kriviznoj.
- CHto za d'yavol'shchina, - voskliknul mister SHell, - moi upravlyayushchie v
Amerike nichego ne smyslyat v svoem dele! Nu skazhite na milost', zachem im
ponadobilos' sosredotachivat' zapravochnye stancii v okrestnostyah Kanzas-Siti?
Prav li mister SHell v svoem zaklyuchenii?
- V samom dele, prav li on? - povtoril mister Tompkins, mysli kotorogo
gde-to vitali.
- Mister SHell gluboko zabluzhdaetsya, - mrachno izrek professor. - On
upustil iz vidu, chto poverhnost' Zemli ne ploskaya, a sfericheskaya, a na sfere
ploshchad', zaklyuchennaya vnutri kruga dannogo radiusa, rastet medlennee, chem na
ploskosti. Mozhete vy predstavit' sebe eto naglyadno? Net? Togda voz'mite
globus i ubedites' sami v tom, chto ya prav. Naprimer, esli vy nahodites' na
Severnom polyuse, to okruzhnost' radiusom v polovinu meridiana est' ne chto
inoe, kak ekvator, a zaklyuchennaya vnutri nee ploshchad' poverhnosti Zemli est'
ploshchad' severnogo polushariya. S uvelicheniem radiusa ploshchad' na poverhnosti
sfery vozrastaet tol'ko vdvoe, a ne vchetvero, kak bylo by na ploskosti.
Teper', nadeyus', yasno?
- O, da, - kivnul mister Tompkins, delaya vid, budto on vnimatel'no
sledit za ob座asneniyami. - A chto takoe polozhitel'naya ili otricatel'naya
krivizna?
- U sfery krivizna schitaetsya polozhitel'noj. Kak vy videli na primere
zemnogo shara, polozhitel'naya krivizna sootvetstvuet konechnoj poverhnosti,
imeyushchej konechnuyu ploshchad'. Primerom poverhnosti s otricatel'noj kriviznoj
mozhet sluzhit' sedlo.
- Sedlo? - peresprosil mister Tompkins.
- Da, sedlo, ili na poverhnosti Zemli sedloobraznyj pereval mezhdu dvumya
gornymi vershinami. Predpolozhim, chto nekij botanik obitaet v gornoj hizhine,
raspolozhennoj na takom sedlovidnom perevale, i zanimaetsya izucheniem
plotnosti sosen, rastushchih vokrug ego zhilishcha. Podschitav chislo sosen, rastushchih
ne dalee sta, dvuhsot, trehsot i t. d. futov ot hizhiny, on obnaruzhit, chto
chislo sosen vozrastaet bystree, chem kvadrat rasstoyaniya, poskol'ku na
sedlovidnoj poverhnosti ploshchad', zaklyuchennaya vnutri dannogo radiusa, rastet
bystree, chem na ploskosti. O takih poverhnostyah govoryat, chto oni obladayut
otricatel'noj kriviznoj. Esli vy popytaetes', rastyanuv, nalozhit' sedlovidnuyu
poverhnost' na ploskost', to vam pridetsya sdelat' skladki. Esli zhe vy
zadumaete nalozhit' na ploskost' sfericheskuyu poverhnost', to vam pridetsya
gde-to prodelat' v nej dyrochku.
- Kazhetsya, ya nachinayu ponimat', - zadumchivo proiznes mister Tompkins. -
Vy hotite skazat', chto sedlovidnaya poverhnost' beskonechnaya, hotya i
iskrivlennaya.
- Vot imenno! - odobritel'no kivnul professor. - Sedlovidnaya
poverhnost' prostiraetsya vo vse storony do beskonechnosti i nigde ne
zamykaetsya. Razumeetsya, v moem primere s sedlovidnym perevalom poverhnost'
perestaet byt' poverhnost'yu otricatel'noj krivizny, kak tol'ko vy
spuskaetes' s gor, i perehodit v iskrivlennuyu poverhnost' zemnogo shara s
polozhitel'noj kriviznoj. No, razumeetsya, nichto ne meshaet vam voobrazit'
poverhnost', sohranyayushchuyu povsyudu otricatel'nuyu kriviznu.
- No kakoe otnoshenie imeet vse eto k iskrivlennomu trehmernomu
prostranstvu?
- Samoe neposredstvennoe. Predstav'te sebe, chto kakie-to vashi ob容kty
ravnomerno raspredeleny po vsemu prostranstvu. Pod ravnomernym ya ponimayu
takoe raspredelenie, pri kotorom rasstoyanie mezhdu lyubymi sosednimi ob容ktami
vsegda odno i to zhe. Predpolozhim, chto vy podschityvaete chislo ob容ktov,
raspolozhennyh ne dalee togo ili inogo rasstoyaniya ot vas. Esli eto chislo
rastet kak kvadrat rasstoyaniya, to prostranstvo ploskoe. Esli zhe chislo
ob容ktov rastet medlennee ili bystree, to prostranstvo obladaet
sootvetstvenno polozhitel'noj ili otricatel'noj kriviznoj.
 - Znachit, v sluchae prostranstva polozhitel'noj krivizny ob容m,
zaklyuchennyj v predelah dannogo rasstoyaniya, men'she, a v sluchae prostranstva
otricatel'noj krivizny - bol'she, chem v sluchae ploskogo prostranstva? - s
udivleniem sprosil mister Tompkins.
- Vot imenno! - ulybnulsya professor. - YA vizhu, chto teper' vy ponyali
menya pravil'no. CHtoby opredelit' znak krivizny toj ogromnoj Vselennoj, v
kotoroj my zhivem, neobhodimo lish' proizvodit' takie podschety udalennyh
ob容ktov. Bol'shie tumannosti, o kotoryh vy, vozmozhno, slyshali, rasseyany
ravnomerno v kosmicheskom prostranstve, i ih mozhno nablyudat' vplot' do
rasstoyanij v neskol'ko millionov svetovyh let. Dlya issledovaniya krivizny
Vselennoj eto ochen' udobnye ob容kty.
- I poluchaetsya, chto nasha Vselennaya konechna i zamknuta?
- Vidite li, - otvetil professor, - v dejstvitel'nosti eta problema vse
eshche ne reshena. V svoih rabotah po kosmologii |jnshtejn utverzhdal, chto nasha
Vselennaya imeet konechnye razmery, zamknuta i ne izmenyaetsya vo vremeni.
Odnako v bolee pozdnej rabote russkogo matematika Al. Fridmana bylo
pokazano, chto fundamental'nye uravneniya |jnshtejna dopuskayut takuyu
vozmozhnost', kak rasshirenie ili szhatie Vselennoj na bolee pozdnem etape
razvitiya. |to matematicheskoe zaklyuchenie bylo podtverzhdeno amerikanskim
astronomom |. Habblom, kotoryj, ispol'zuya stodyujmovyj teleskop observatorii
Maunt Vilson, obnaruzhil, chto galaktiki razletayutsya, t.e. nasha Vselennaya
rasshiryaetsya. Sushchestvuet, odnako, vse eshche nereshennaya problema otnositel'no
togo, budet li eto rasshirenie prodolzhat'sya neogranichenno ili radius
Vselennoj dostignet svoego maksimal'nogo znacheniya, posle chego v otdalennom
budushchem rasshirenie smenitsya szhatiem. Otvet na etot vopros mogut dat' tol'ko
bolee podrobnye astronomicheskie nablyudeniya.
Poka professor govoril, vokrug stali proishodit' ves'ma neobychnye
izmeneniya: odin konec koridora szhalsya i stal krohotnym, sdaviv vsyu stoyavshuyu
tam mebel', zato drugoj konec rasshirilsya i prodolzhal uvelichivat'sya v
razmerah, hotya uzhe sejchas, kak pokazalos' misteru Tompkinsu, on mog vmestit'
vsyu Vselennuyu. Uzhasnaya mysl' proneslas' v golove mistera Tompkinsa: chto esli
kusochek prostranstva s plyazhem, gde miss Mod risovala svoi etyudy, otorvalsya
ot osnovnoj chasti Vselennoj? - Togda, - podumal mister Tompkins, - ya nikogda
ne uvizhu ee snova!
Mister Tompkins brosilsya k vyhodu. Poslednee, chto on uslyshal, byl golos
professora, krichavshego emu vsled:
- Ostorozhnee! Kvantovaya postoyannaya takzhe shodit s uma!
Kogda mister Tompkins dostig plyazha, emu pokazalos', chto on perepolnen.
Tysyachi devushek nosilis' po vsem napravleniyam, sozdavaya dikuyu nerazberihu.
- Kak zhe ya smogu najti moyu Mod v etoj tolpe? - rasteryanno podumal
mister Tompkins. No priglyadevshis', on zametil, chto vse devushki vyglyadeli
tochno tak zhe, kak doch' professora, i ponyal, chto eto neobychajnoe shodstvo
bylo igroj principa neopredelennosti. V sleduyushchij moment volna anomal'no
bol'shoj kvantovoj postoyannoj proshla, i pered misterom Tompkinsom na plyazhe
okazalas' miss Mod s ispugannym vyrazheniem v glazah.
- Ah, eto vy! - vzdohnula ona s oblegcheniem. - A mne pokazalos', chto
ogromnaya tolpa zatopchet menya. Dolzhno byt', ya peregrelas' na solnce i eto mne
pomereshchilos'. Podozhdite, pozhalujsta, menya zdes', ya tol'ko na minutku sbegayu
v otel' za shlyapoj.
- Net-net, my ne dolzhny rasstavat'sya, - zaprotestoval mister Tompkins.
- Mne kazhetsya, chto skorost' sveta takzhe menyaetsya. Vernuvshis' so shlyapoj, vy
mozhete zastat' menya dryahlym starikom.
- Ne govorite chepuhi, - vozrazila devushka, no vzyala mistera Tompkinsa
pod ruku. A na polputi k otelyu novaya volna neopredelennosti nakryla ih, i
mister Tompkins i ego sputnica okazalis' razmazannymi po vsemu beregu.
Odnovremenno s okrestnyh holmov nachala rasprostranyat'sya skladka
prostranstva, prichudlivo iskazhaya ochertaniya pribrezhnyh skal i rybackih
domikov. Luchi Solnca, otrazhennye ot intensivnogo gravitacionnogo polya,
polnost'yu ischezli za gorizontom, i mister Tompkins pogruzilsya v kromeshnuyu
t'mu.
Proshla celaya vechnost', prezhde chem stol' milyj ego serdcu golos ne
privel ego v chuvstvo.
- O, ya vizhu moj papochka sovsem usypil vas svoimi razgovorami o fizike,
- proshchebetala miss Mod. - Ne hotite li vy pojti so mnoj poplavat'? Voda
segodnya prosto velikolepnaya.
Mister Tompkins podprygnul so svoego legkogo kresla, kak na pruzhinah.
- Tak eto byl tol'ko son, - podumal on, kogda oni spuskalis' k plyazhu. -
Ili son tol'ko teper' nachinaetsya?
Lekciya professora ob iskrivlennom prostranstve, gravitacii i vselennoj
Ledi i dzhentl'meny!
Segodnya ya namerevayus' rassmotret' problemu iskrivlennogo prostranstva i
ee svyaz' s yavleniyami gravitacii. Ne somnevayus', chto kazhdyj iz vas bez truda
mozhet predstavit' sebe iskrivlennuyu liniyu (krivuyu) ili iskrivlennuyu
poverhnost', no pri upominanii ob iskrivlennom trehmernom prostranstve vashi
lica vytyagivayutsya i vy sklonny dumat', chto eto nechto ves'ma neobychnoe i
pochti sverh容stestvennoe. Pochemu iskrivlennoe prostranstvo vyzyvaet vseobshchij
"uzhas"? Dejstvitel'no li ponyatie iskrivlennogo prostranstva trudnee dlya
ponimaniya, chem ponyatie iskrivlennoj poverhnosti? Mnogie iz vas, porazmysliv
nemnogo nad etimi voprosami, veroyatno, skazhut, chto predstavit' iskrivlennoe
trehmernoe prostranstvo trudnee po odnoj-edinstvennoj prichine: my ne mozhem
vzglyanut' na prostranstvo "so storony", kak my smotrim na iskrivlennuyu
poverhnost' shara, ili, esli obratit'sya k drugomu primeru, na takuyu osobym
obrazom izognutuyu poverhnost', kak sedlo. No te, kto tak govoryat, obrekayut
sebya na neznanie strogo matematicheskogo smysla krivizny, sushchestvenno
otlichayushchegosya ot obshcheupotreblyaemogo znacheniya etogo slova. My, matematiki,
nazyvaem poverhnost' iskrivlennoj, esli svojstva geometricheskih figur,
nacherchennyh na nej, otlichny ot svojstv figur na ploskosti, i izmeryaem
kriviznu otkloneniem ot klassicheskih pravil Evklida. Esli vy nachertite
treugol'nik na ploskom liste bumagi, to, kak izvestno iz elementarnoj
geometrii, summa ego vnutrennih uglov ravna dvum pryamym. Vy mozhete izognut'
etot list bumagi, pridav emu formu cilindra, konusa ili kakoj-nibud' bolee
slozhnoj figury, no summa uglov nacherchennogo na nem treugol'nika neizmenno
budet ostavat'sya ravnoj dvum pryamym uglam.
Geometriya poverhnosti ne menyaetsya pri etih deformaciyah i s tochki zreniya
"vnutrennej" krivizny poluchayushchiesya poverhnosti (iskrivlennye v obychnom
smysle) takie zhe ploskie, kak obychnaya ploskost'. No vy ne mozhete nalozhit'
list bumagi, ne rastyagivaya ego, na poverhnost' sfery ili sedla, a esli vy
nachertite treugol'nik na poverhnosti sfery (t.e. postroite sfericheskij
treugol'nik), to prostye teoremy evklidovoj geometrii vypolnyat'sya ne budut.
Naprimer, treugol'nik, obrazovannyj severnymi polovinami meridianov i
zaklyuchennoj mezhdu nimi dugoj ekvatora, imeet dva pryamyh ugla pri osnovanii i
proizvol'nyj ugol pri vershine.
Vozmozhno, vy udivites', kogda uznaete, chto na sedlovidnoj poverhnosti
summa uglov treugol'nika, naoborot, vsegda men'she dvuh pryamyh.
Takim obrazom, _chtoby opredelit' kriviznu poverhnosti, neobhodimo
izuchit' geometriyu na etoj poverhnosti_. Vzglyad zhe izvne na poverhnost' chasto
byvaet oshibochnym. Glyadya na poverhnost' izvne, vy skoree vsego otnesli by
poverhnost' cilindra k tomu zhe klassu, chto i poverhnost' obruchal'nogo
kol'ca. Mezhdu tem pervaya poverhnost' ploskaya, a vtoraya neizlechimo
iskrivlena. Kak tol'ko vy privyknite k etomu novomu strogomu ponyatiyu
krivizny, u vas ne budet bolee nikakih trudnostej v ponimanii togo, chto
imeyut v vidu fiziki, rassuzhdaya o tom, iskrivleno ili plosko prostranstvo, v
kotorom my zhivem. Problema zaklyuchaetsya tol'ko v vyyasnenii togo, podchinyayutsya
ili ne podchinyayutsya obychnym pravilam evklidovoj geometrii geometricheskie
figury, postroennye v fizicheskom prostranstve.
No poskol'ku my govorim o real'nom fizicheskom prostranstve, nam
neobhodimo prezhde vsego dat' _fizicheskoe opredelenie terminov, ispol'zuemyh
v geometrii_, i, v chastnosti, ukazat', chto my ponimaem pod pryamymi, iz
kotoryh postroeny figury.
- Znachit, v sluchae prostranstva polozhitel'noj krivizny ob容m,
zaklyuchennyj v predelah dannogo rasstoyaniya, men'she, a v sluchae prostranstva
otricatel'noj krivizny - bol'she, chem v sluchae ploskogo prostranstva? - s
udivleniem sprosil mister Tompkins.
- Vot imenno! - ulybnulsya professor. - YA vizhu, chto teper' vy ponyali
menya pravil'no. CHtoby opredelit' znak krivizny toj ogromnoj Vselennoj, v
kotoroj my zhivem, neobhodimo lish' proizvodit' takie podschety udalennyh
ob容ktov. Bol'shie tumannosti, o kotoryh vy, vozmozhno, slyshali, rasseyany
ravnomerno v kosmicheskom prostranstve, i ih mozhno nablyudat' vplot' do
rasstoyanij v neskol'ko millionov svetovyh let. Dlya issledovaniya krivizny
Vselennoj eto ochen' udobnye ob容kty.
- I poluchaetsya, chto nasha Vselennaya konechna i zamknuta?
- Vidite li, - otvetil professor, - v dejstvitel'nosti eta problema vse
eshche ne reshena. V svoih rabotah po kosmologii |jnshtejn utverzhdal, chto nasha
Vselennaya imeet konechnye razmery, zamknuta i ne izmenyaetsya vo vremeni.
Odnako v bolee pozdnej rabote russkogo matematika Al. Fridmana bylo
pokazano, chto fundamental'nye uravneniya |jnshtejna dopuskayut takuyu
vozmozhnost', kak rasshirenie ili szhatie Vselennoj na bolee pozdnem etape
razvitiya. |to matematicheskoe zaklyuchenie bylo podtverzhdeno amerikanskim
astronomom |. Habblom, kotoryj, ispol'zuya stodyujmovyj teleskop observatorii
Maunt Vilson, obnaruzhil, chto galaktiki razletayutsya, t.e. nasha Vselennaya
rasshiryaetsya. Sushchestvuet, odnako, vse eshche nereshennaya problema otnositel'no
togo, budet li eto rasshirenie prodolzhat'sya neogranichenno ili radius
Vselennoj dostignet svoego maksimal'nogo znacheniya, posle chego v otdalennom
budushchem rasshirenie smenitsya szhatiem. Otvet na etot vopros mogut dat' tol'ko
bolee podrobnye astronomicheskie nablyudeniya.
Poka professor govoril, vokrug stali proishodit' ves'ma neobychnye
izmeneniya: odin konec koridora szhalsya i stal krohotnym, sdaviv vsyu stoyavshuyu
tam mebel', zato drugoj konec rasshirilsya i prodolzhal uvelichivat'sya v
razmerah, hotya uzhe sejchas, kak pokazalos' misteru Tompkinsu, on mog vmestit'
vsyu Vselennuyu. Uzhasnaya mysl' proneslas' v golove mistera Tompkinsa: chto esli
kusochek prostranstva s plyazhem, gde miss Mod risovala svoi etyudy, otorvalsya
ot osnovnoj chasti Vselennoj? - Togda, - podumal mister Tompkins, - ya nikogda
ne uvizhu ee snova!
Mister Tompkins brosilsya k vyhodu. Poslednee, chto on uslyshal, byl golos
professora, krichavshego emu vsled:
- Ostorozhnee! Kvantovaya postoyannaya takzhe shodit s uma!
Kogda mister Tompkins dostig plyazha, emu pokazalos', chto on perepolnen.
Tysyachi devushek nosilis' po vsem napravleniyam, sozdavaya dikuyu nerazberihu.
- Kak zhe ya smogu najti moyu Mod v etoj tolpe? - rasteryanno podumal
mister Tompkins. No priglyadevshis', on zametil, chto vse devushki vyglyadeli
tochno tak zhe, kak doch' professora, i ponyal, chto eto neobychajnoe shodstvo
bylo igroj principa neopredelennosti. V sleduyushchij moment volna anomal'no
bol'shoj kvantovoj postoyannoj proshla, i pered misterom Tompkinsom na plyazhe
okazalas' miss Mod s ispugannym vyrazheniem v glazah.
- Ah, eto vy! - vzdohnula ona s oblegcheniem. - A mne pokazalos', chto
ogromnaya tolpa zatopchet menya. Dolzhno byt', ya peregrelas' na solnce i eto mne
pomereshchilos'. Podozhdite, pozhalujsta, menya zdes', ya tol'ko na minutku sbegayu
v otel' za shlyapoj.
- Net-net, my ne dolzhny rasstavat'sya, - zaprotestoval mister Tompkins.
- Mne kazhetsya, chto skorost' sveta takzhe menyaetsya. Vernuvshis' so shlyapoj, vy
mozhete zastat' menya dryahlym starikom.
- Ne govorite chepuhi, - vozrazila devushka, no vzyala mistera Tompkinsa
pod ruku. A na polputi k otelyu novaya volna neopredelennosti nakryla ih, i
mister Tompkins i ego sputnica okazalis' razmazannymi po vsemu beregu.
Odnovremenno s okrestnyh holmov nachala rasprostranyat'sya skladka
prostranstva, prichudlivo iskazhaya ochertaniya pribrezhnyh skal i rybackih
domikov. Luchi Solnca, otrazhennye ot intensivnogo gravitacionnogo polya,
polnost'yu ischezli za gorizontom, i mister Tompkins pogruzilsya v kromeshnuyu
t'mu.
Proshla celaya vechnost', prezhde chem stol' milyj ego serdcu golos ne
privel ego v chuvstvo.
- O, ya vizhu moj papochka sovsem usypil vas svoimi razgovorami o fizike,
- proshchebetala miss Mod. - Ne hotite li vy pojti so mnoj poplavat'? Voda
segodnya prosto velikolepnaya.
Mister Tompkins podprygnul so svoego legkogo kresla, kak na pruzhinah.
- Tak eto byl tol'ko son, - podumal on, kogda oni spuskalis' k plyazhu. -
Ili son tol'ko teper' nachinaetsya?
Lekciya professora ob iskrivlennom prostranstve, gravitacii i vselennoj
Ledi i dzhentl'meny!
Segodnya ya namerevayus' rassmotret' problemu iskrivlennogo prostranstva i
ee svyaz' s yavleniyami gravitacii. Ne somnevayus', chto kazhdyj iz vas bez truda
mozhet predstavit' sebe iskrivlennuyu liniyu (krivuyu) ili iskrivlennuyu
poverhnost', no pri upominanii ob iskrivlennom trehmernom prostranstve vashi
lica vytyagivayutsya i vy sklonny dumat', chto eto nechto ves'ma neobychnoe i
pochti sverh容stestvennoe. Pochemu iskrivlennoe prostranstvo vyzyvaet vseobshchij
"uzhas"? Dejstvitel'no li ponyatie iskrivlennogo prostranstva trudnee dlya
ponimaniya, chem ponyatie iskrivlennoj poverhnosti? Mnogie iz vas, porazmysliv
nemnogo nad etimi voprosami, veroyatno, skazhut, chto predstavit' iskrivlennoe
trehmernoe prostranstvo trudnee po odnoj-edinstvennoj prichine: my ne mozhem
vzglyanut' na prostranstvo "so storony", kak my smotrim na iskrivlennuyu
poverhnost' shara, ili, esli obratit'sya k drugomu primeru, na takuyu osobym
obrazom izognutuyu poverhnost', kak sedlo. No te, kto tak govoryat, obrekayut
sebya na neznanie strogo matematicheskogo smysla krivizny, sushchestvenno
otlichayushchegosya ot obshcheupotreblyaemogo znacheniya etogo slova. My, matematiki,
nazyvaem poverhnost' iskrivlennoj, esli svojstva geometricheskih figur,
nacherchennyh na nej, otlichny ot svojstv figur na ploskosti, i izmeryaem
kriviznu otkloneniem ot klassicheskih pravil Evklida. Esli vy nachertite
treugol'nik na ploskom liste bumagi, to, kak izvestno iz elementarnoj
geometrii, summa ego vnutrennih uglov ravna dvum pryamym. Vy mozhete izognut'
etot list bumagi, pridav emu formu cilindra, konusa ili kakoj-nibud' bolee
slozhnoj figury, no summa uglov nacherchennogo na nem treugol'nika neizmenno
budet ostavat'sya ravnoj dvum pryamym uglam.
Geometriya poverhnosti ne menyaetsya pri etih deformaciyah i s tochki zreniya
"vnutrennej" krivizny poluchayushchiesya poverhnosti (iskrivlennye v obychnom
smysle) takie zhe ploskie, kak obychnaya ploskost'. No vy ne mozhete nalozhit'
list bumagi, ne rastyagivaya ego, na poverhnost' sfery ili sedla, a esli vy
nachertite treugol'nik na poverhnosti sfery (t.e. postroite sfericheskij
treugol'nik), to prostye teoremy evklidovoj geometrii vypolnyat'sya ne budut.
Naprimer, treugol'nik, obrazovannyj severnymi polovinami meridianov i
zaklyuchennoj mezhdu nimi dugoj ekvatora, imeet dva pryamyh ugla pri osnovanii i
proizvol'nyj ugol pri vershine.
Vozmozhno, vy udivites', kogda uznaete, chto na sedlovidnoj poverhnosti
summa uglov treugol'nika, naoborot, vsegda men'she dvuh pryamyh.
Takim obrazom, _chtoby opredelit' kriviznu poverhnosti, neobhodimo
izuchit' geometriyu na etoj poverhnosti_. Vzglyad zhe izvne na poverhnost' chasto
byvaet oshibochnym. Glyadya na poverhnost' izvne, vy skoree vsego otnesli by
poverhnost' cilindra k tomu zhe klassu, chto i poverhnost' obruchal'nogo
kol'ca. Mezhdu tem pervaya poverhnost' ploskaya, a vtoraya neizlechimo
iskrivlena. Kak tol'ko vy privyknite k etomu novomu strogomu ponyatiyu
krivizny, u vas ne budet bolee nikakih trudnostej v ponimanii togo, chto
imeyut v vidu fiziki, rassuzhdaya o tom, iskrivleno ili plosko prostranstvo, v
kotorom my zhivem. Problema zaklyuchaetsya tol'ko v vyyasnenii togo, podchinyayutsya
ili ne podchinyayutsya obychnym pravilam evklidovoj geometrii geometricheskie
figury, postroennye v fizicheskom prostranstve.
No poskol'ku my govorim o real'nom fizicheskom prostranstve, nam
neobhodimo prezhde vsego dat' _fizicheskoe opredelenie terminov, ispol'zuemyh
v geometrii_, i, v chastnosti, ukazat', chto my ponimaem pod pryamymi, iz
kotoryh postroeny figury.
 Dumayu, vse vy znaete, chto pryamuyu chashche vsego opredelyayut kak kratchajshee
rasstoyanie mezhdu dvumya tochkami. Pryamuyu mozhno postroit', libo natyanuv nit'
mezhdu dvumya tochkami, libo s pomoshch'yu kakogo-nibud' ekvivalentnogo, no bolee
slozhnogo processa, ustanoviv opytnym putem liniyu mezhdu dvumya dannymi
tochkami, vdol' kotoroj minimal'noe chislo raz ukladyvaetsya mernyj sterzhen'
dannoj dliny.
CHtoby pokazat', chto rezul'taty postroeniya pryamoj s pomoshch'yu takogo
metoda zavisyat ot fizicheskih uslovij, predstavim sebe bol'shuyu krugluyu
platformu, ravnomerno vrashchayushchuyusya vokrug svoej osi {Nazvanie "Cirk Hukhema"
voshodit k misteru Dzhonu Hukhemu, rabotavshemu hudozhnikom-illyustratorom v
izdatel'stve Kembridzhskogo universiteta. Nezadolgo do vyhoda v otstavku
mister Hukhem sozdal mnogie iz risunkov, ukrasivshih etu knigu.}, i pust'
eksperimentator |2 pytaetsya najti kratchajshee rasstoyanie mezhdu dvumya tochkami
na krayu platformy. U eksperimentatora imeetsya korobka s ogromnym chislom
sterzhnej, kazhdyj dlinoj 5 dyujmov, i on pytaetsya vylozhit' iz minimal'nogo
chisla etih sterzhnej liniyu, soedinyayushchuyu dve dannye tochki A i V. Esli by
platforma ne vrashchalas', to nash eksperimentator raspolozhil by sterzhni vdol'
shtrihovoj linii mezhdu tochkami A i V. No iz-za vrashcheniya platformy ego mernye
sterzhni preterpevayut relyativistskoe sokrashchenie, o kotorom ya rasskazal vam v
moej predydushchej lekcii, prichem te iz nih, kotorye raspolozheny blizhe k krayu
platformy (i, sledovatel'no, obladayut bol'shimi linejnymi skorostyami),
sokrashchayutsya sil'nee, chem sterzhni, raspolozhennye blizhe k centru. YAsno, chto
dlya togo chtoby kazhdyj sterzhen' pokryval kak mozhno bol'shee rasstoyanie,
sterzhni neobhodimo raspolagat' kak mozhno blizhe k centru. No poskol'ku oba
konca linii zakrepleny na krayu platformy, sdvigat' vse sterzhni ot serediny
linii slishkom blizko k centru nevygodno.
V rezul'tate nash fizik dostignet nekoego kompromissa mezhdu etimi dvumya
usloviyami, i _kratchajshee rasstoyanie budet v konce koncov predstavleno
krivoj, slegka vypukloj v storonu centra_.
Esli nash eksperimentator vmesto otdel'nyh sterzhnej natyanet mezhdu dvumya
dannymi tochkami A i V nit', to rezul'tat, kak netrudno ponyat', poluchitsya
prezhnim, poskol'ku kazhdyj otrezok niti preterpevaet takoe zhe relyativistskoe
sokrashchenie, kak otdel'nye sterzhni. YA hochu osobo podcherknut', chto
relyativistskaya deformaciya natyanutoj niti, proishodyashchaya, kogda platforma
nachinaet vrashchat'sya, ne imeet nichego obshchego s obychnymi effektami centrobezhnoj
sily. Relyativistskaya deformaciya ostaetsya neizmennoj, kak by sil'no ni byla
natyanuta nit', ne govorya uzhe o tom, chto obychnaya centrobezhnaya sila dejstvuet
v protivopolozhnom napravlenii.
Esli nablyudatel', nahodyashchijsya na platforme, vzdumaet proverit'
rezul'tat svoih postroenij, sravniv poluchennuyu "pryamuyu" s luchom sveta, to on
obnaruzhit, chto svet dejstvitel'no rasprostranyaetsya vdol' postroennoj im
linii. Razumeetsya, dlya nablyudatelej, stoyashchih u platformy, luch sveta voobshche
ne budet iskrivlen. Oni budut interpretirovat' rezul'taty dvizhushchegosya
nablyudatelya putem superpozicii, ili nalozheniya, vrashcheniya platformy i
pryamolinejnogo rasprostraneniya sveta. Oni skazhut vam, chto esli vy nanesete
carapinu na vrashchayushchuyusya grammofonnuyu plastinku, dvinuv rukoj po pryamoj, to
carapina na plastinke, konechno zhe, budet iskrivlennoj.
No dlya nablyudatelya, nahodyashchegosya na vrashchayushchejsya platforme, nazvanie
"pryamaya" dlya postroennoj im krivoj vpolne razumno: eta krivaya daet
_kratchajshee rasstoyanie_ i sovpadaet s _luchom sveta_ v sisteme otscheta nashego
nablyudatelya. Predpolozhim, chto on vybral na krayu platformy tri tochki i
soedinil ih pryamymi, postroiv tem samym treugol'nik. _Summa uglov v etom
treugol'nike men'she dvuh pryamyh_, iz chego nash nablyudatel' zaklyuchaet (i
sovershenno spravedlivo), chto prostranstvo vokrug nego iskrivleno.
Rassmotrim drugoj primer. Predpolozhim, chto dva drugih nablyudatelya na
platforme (|3 i |4) reshili ocenit' chislo pi, izmeryaya dlinu okruzhnosti
platformy i ee diametr. Na mernyj sterzhen' nablyudatelya |3 vrashchenie ne
vliyaet, poskol'ku dvizhenie sterzhnya vsegda perpendikulyarno ego dline. S
drugoj storony, mernyj sterzhen' nablyudatelya |4 vsegda budet sokrashchen, i dlya
dliny okruzhnosti platformy etot nablyudatel' poluchit bol'shee znachenie, chem v
sluchae nevrashchayushchejsya platformy. Delya rezul'tat, poluchennyj nablyudatelem 4,
na rezul'tat, poluchennyj nablyudatelem 3, my poluchim znachenie, prevyshayushchee
znachenie pi, obychno privodimoe v uchebnikah. |to takzhe yavlyaetsya sledstviem
krivizny prostranstva.
Vrashchenie vliyaet ne tol'ko na izmereniya dlin. CHasy, raspolozhennye na
krayu platformy, budut dvigat'sya s bol'shej skorost'yu i, kak bylo pokazano v
predydushchej lekcii, ih hod zamedlitsya po sravneniyu s hodom chasov,
ustanovlennyh v centre platformy.
Esli dva eksperimentatora (|4 i |5) sveryat chasy v centre platformy, a
zatem eksperimentator |5 na kakoe-to vremya otneset svoi chasy na kraj
platformy, to po vozvrashchenii v centr on obnaruzhit, chto ego chasy otstayut po
sravneniyu s chasami, vse vremya ostavavshimisya v centre platformy. Iz etogo
eksperimentator |5 sdelaet vyvod, chto v razlichnyh mestah platformy vse
fizicheskie processy idut s razlichnymi skorostyami. Predpolozhim teper', chto
nashi eksperimentatory ostanovilis' i nemnogo porazmyslili nad prichinoj
neobychnyh rezul'tatov, tol'ko chto poluchennyh imi v geometricheskih
izmereniyah. Predpolozhim takzhe, chto vrashchayushchayasya platforma zakryta so vseh
storon i predstavlyaet soboj vrashchayushchuyusya komnatu bez okon, chtoby
eksperimentatory ne mogli nablyudat' svoe dvizhenie otnositel'no okruzhayushchih
predmetov. Mogli by v etom sluchae eksperimentatory ob座asnit' vse poluchennye
rezul'taty chisto fizicheskimi usloviyami na platforme bez ucheta ee vrashcheniya
otnositel'no "tverdoj osnovy", na kotoroj ustanovlena platforma?
Glyadya na razlichiya mezhdu fizicheskimi usloviyami na platforme i na
"tverdoj osnove", posredstvom kotoryh mozhno bylo by ob座asnit' nablyudaemye
izmeneniya v geometrii, nashi eksperimentatory srazu zhe zametili by, chto
sushchestvuet kakaya-to novaya sila, kotoraya stremitsya otbrosit' vse tela ot
centra platformy k ee okruzhnosti. Vpolne estestvenno, chto oni pripisali by
nablyudaemye effekty dejstviyu etoj sily, utverzhdaya, naprimer, chto iz dvuh
chasov te budut idti medlennee, kotorye raspolozheny dal'she ot centra v
napravlenii novoj sily.
No dejstvitel'no li eta novaya sila nova, t. e. ne nablyudaema na
"tverdoj osnove"? Razve my ne nablyudaem, kak vse tela prityagivayutsya k centru
Zemli siloj, kotoraya poluchila nazvanie sily tyazhesti? Razumeetsya, v odnom
sluchae my imeem prityazhenie k okruzhnosti diska, v drugom - prityazhenie k
centru Zemli, no eto oznachaet tol'ko razlichie v raspredelenii sily.
Netrudno, odnako, privesti drugoj primer, kogda "novaya" sila, porozhdaemaya
neravnomernym dvizheniem sistemy otscheta, vyglyadit tochno tak zhe, kak sila
tyazhesti v etoj lekcionnoj auditorii.
Predpolozhim, chto kosmicheskij korabl', prednaznachennyj dlya mezhzvezdnyh
pereletov, svobodno letit gde-to v kosmicheskom prostranstve nastol'ko daleko
ot razlichnyh zvezd, chto vnutri korablya sila tyazhesti ne dejstvuet. Vse
predmety vnutri kosmicheskogo korablya i sami puteshestvuyushchie v nem
eksperimentatory nevesomy i svobodno plavayut v vozduhe primerno tak zhe, kak
Mishel' Ardan i ego sputniki vo vremya puteshestviya na Lunu v znamenitom romane
ZHyulya Verna.
No vot dvigateli vklyucheny i kosmicheskij korabl' prihodit v dvizhenie,
postepenno nabiraya skorost'. CHto proishodit vnutri nego? Netrudno videt',
chto poka kosmicheskij korabl' uskoryaetsya, vse predmety vnutri nego
obnaruzhivayut stremlenie dvigat'sya k polu, ili, chto to zhe, pol dvizhetsya
navstrechu etim predmetam. Naprimer, esli nash eksperimentator derzhit v ruke
yabloko i vypuskaet ego, to yabloko prodolzhaet dvigat'sya (otnositel'no
okruzhayushchih korabl' zvezd) s postoyannoj skorost'yu - toj samoj, s kotoroj
dvigalsya kosmicheskij korabl', kogda eksperimentator vypustil iz ruk yabloko.
No kosmicheskij korabl' uskoryaetsya. Sledovatel'no, pol kabiny, dvigayas' vse
bystree i bystree, v konce koncov dogonit yabloko i stuknet ego. S etogo
momenta yabloko ostanetsya v postoyannom kontakte s polom, buduchi prizhato k
polu postoyanno dejstvuyushchim uskoreniem.
No dlya eksperimentatora, nahodyashchegosya vnutri kosmicheskogo korablya, vse
vyglyadit inache: yabloko "padaet" s kakim-to uskoreniem i, udarivshis' ob pol,
ostaetsya lezhat' na polu, pridavlennoe k nemu sobstvennym vesom. Brosaya
razlichnye predmety, nash eksperimentator zametit, chto vse oni padayut s
sovershenno odinakovym uskoreniem (esli prenebrech' treniem o vozduh) i
vspomnit, chto eto - zakon svobodnogo padeniya, otkrytyj Galileo Galileem. _No
nash eksperimentator tak i ne smozhet zametit' ni malejshego razlichiya mezhdu
yavleniyami, proishodyashchimi v dvizhushchejsya s uskoreniem kabine kosmicheskogo
korablya i obychnymi yavleniyami gravitacii. On mozhet pol'zovat'sya mayatnikovymi
chasami, stavit' knigi na polku, ne boyas', chto te uletyat proch', i povesit' na
gvozd' portret Al'berta |jnshtejna, kotoryj pervym ukazal na ekvivalentnost'
uskoreniya sistemy otscheta i gravitacii i na etoj osnove razvil tak
nazyvaemuyu obshchuyu teoriyu otnositel'nosti_.
Dumayu, vse vy znaete, chto pryamuyu chashche vsego opredelyayut kak kratchajshee
rasstoyanie mezhdu dvumya tochkami. Pryamuyu mozhno postroit', libo natyanuv nit'
mezhdu dvumya tochkami, libo s pomoshch'yu kakogo-nibud' ekvivalentnogo, no bolee
slozhnogo processa, ustanoviv opytnym putem liniyu mezhdu dvumya dannymi
tochkami, vdol' kotoroj minimal'noe chislo raz ukladyvaetsya mernyj sterzhen'
dannoj dliny.
CHtoby pokazat', chto rezul'taty postroeniya pryamoj s pomoshch'yu takogo
metoda zavisyat ot fizicheskih uslovij, predstavim sebe bol'shuyu krugluyu
platformu, ravnomerno vrashchayushchuyusya vokrug svoej osi {Nazvanie "Cirk Hukhema"
voshodit k misteru Dzhonu Hukhemu, rabotavshemu hudozhnikom-illyustratorom v
izdatel'stve Kembridzhskogo universiteta. Nezadolgo do vyhoda v otstavku
mister Hukhem sozdal mnogie iz risunkov, ukrasivshih etu knigu.}, i pust'
eksperimentator |2 pytaetsya najti kratchajshee rasstoyanie mezhdu dvumya tochkami
na krayu platformy. U eksperimentatora imeetsya korobka s ogromnym chislom
sterzhnej, kazhdyj dlinoj 5 dyujmov, i on pytaetsya vylozhit' iz minimal'nogo
chisla etih sterzhnej liniyu, soedinyayushchuyu dve dannye tochki A i V. Esli by
platforma ne vrashchalas', to nash eksperimentator raspolozhil by sterzhni vdol'
shtrihovoj linii mezhdu tochkami A i V. No iz-za vrashcheniya platformy ego mernye
sterzhni preterpevayut relyativistskoe sokrashchenie, o kotorom ya rasskazal vam v
moej predydushchej lekcii, prichem te iz nih, kotorye raspolozheny blizhe k krayu
platformy (i, sledovatel'no, obladayut bol'shimi linejnymi skorostyami),
sokrashchayutsya sil'nee, chem sterzhni, raspolozhennye blizhe k centru. YAsno, chto
dlya togo chtoby kazhdyj sterzhen' pokryval kak mozhno bol'shee rasstoyanie,
sterzhni neobhodimo raspolagat' kak mozhno blizhe k centru. No poskol'ku oba
konca linii zakrepleny na krayu platformy, sdvigat' vse sterzhni ot serediny
linii slishkom blizko k centru nevygodno.
V rezul'tate nash fizik dostignet nekoego kompromissa mezhdu etimi dvumya
usloviyami, i _kratchajshee rasstoyanie budet v konce koncov predstavleno
krivoj, slegka vypukloj v storonu centra_.
Esli nash eksperimentator vmesto otdel'nyh sterzhnej natyanet mezhdu dvumya
dannymi tochkami A i V nit', to rezul'tat, kak netrudno ponyat', poluchitsya
prezhnim, poskol'ku kazhdyj otrezok niti preterpevaet takoe zhe relyativistskoe
sokrashchenie, kak otdel'nye sterzhni. YA hochu osobo podcherknut', chto
relyativistskaya deformaciya natyanutoj niti, proishodyashchaya, kogda platforma
nachinaet vrashchat'sya, ne imeet nichego obshchego s obychnymi effektami centrobezhnoj
sily. Relyativistskaya deformaciya ostaetsya neizmennoj, kak by sil'no ni byla
natyanuta nit', ne govorya uzhe o tom, chto obychnaya centrobezhnaya sila dejstvuet
v protivopolozhnom napravlenii.
Esli nablyudatel', nahodyashchijsya na platforme, vzdumaet proverit'
rezul'tat svoih postroenij, sravniv poluchennuyu "pryamuyu" s luchom sveta, to on
obnaruzhit, chto svet dejstvitel'no rasprostranyaetsya vdol' postroennoj im
linii. Razumeetsya, dlya nablyudatelej, stoyashchih u platformy, luch sveta voobshche
ne budet iskrivlen. Oni budut interpretirovat' rezul'taty dvizhushchegosya
nablyudatelya putem superpozicii, ili nalozheniya, vrashcheniya platformy i
pryamolinejnogo rasprostraneniya sveta. Oni skazhut vam, chto esli vy nanesete
carapinu na vrashchayushchuyusya grammofonnuyu plastinku, dvinuv rukoj po pryamoj, to
carapina na plastinke, konechno zhe, budet iskrivlennoj.
No dlya nablyudatelya, nahodyashchegosya na vrashchayushchejsya platforme, nazvanie
"pryamaya" dlya postroennoj im krivoj vpolne razumno: eta krivaya daet
_kratchajshee rasstoyanie_ i sovpadaet s _luchom sveta_ v sisteme otscheta nashego
nablyudatelya. Predpolozhim, chto on vybral na krayu platformy tri tochki i
soedinil ih pryamymi, postroiv tem samym treugol'nik. _Summa uglov v etom
treugol'nike men'she dvuh pryamyh_, iz chego nash nablyudatel' zaklyuchaet (i
sovershenno spravedlivo), chto prostranstvo vokrug nego iskrivleno.
Rassmotrim drugoj primer. Predpolozhim, chto dva drugih nablyudatelya na
platforme (|3 i |4) reshili ocenit' chislo pi, izmeryaya dlinu okruzhnosti
platformy i ee diametr. Na mernyj sterzhen' nablyudatelya |3 vrashchenie ne
vliyaet, poskol'ku dvizhenie sterzhnya vsegda perpendikulyarno ego dline. S
drugoj storony, mernyj sterzhen' nablyudatelya |4 vsegda budet sokrashchen, i dlya
dliny okruzhnosti platformy etot nablyudatel' poluchit bol'shee znachenie, chem v
sluchae nevrashchayushchejsya platformy. Delya rezul'tat, poluchennyj nablyudatelem 4,
na rezul'tat, poluchennyj nablyudatelem 3, my poluchim znachenie, prevyshayushchee
znachenie pi, obychno privodimoe v uchebnikah. |to takzhe yavlyaetsya sledstviem
krivizny prostranstva.
Vrashchenie vliyaet ne tol'ko na izmereniya dlin. CHasy, raspolozhennye na
krayu platformy, budut dvigat'sya s bol'shej skorost'yu i, kak bylo pokazano v
predydushchej lekcii, ih hod zamedlitsya po sravneniyu s hodom chasov,
ustanovlennyh v centre platformy.
Esli dva eksperimentatora (|4 i |5) sveryat chasy v centre platformy, a
zatem eksperimentator |5 na kakoe-to vremya otneset svoi chasy na kraj
platformy, to po vozvrashchenii v centr on obnaruzhit, chto ego chasy otstayut po
sravneniyu s chasami, vse vremya ostavavshimisya v centre platformy. Iz etogo
eksperimentator |5 sdelaet vyvod, chto v razlichnyh mestah platformy vse
fizicheskie processy idut s razlichnymi skorostyami. Predpolozhim teper', chto
nashi eksperimentatory ostanovilis' i nemnogo porazmyslili nad prichinoj
neobychnyh rezul'tatov, tol'ko chto poluchennyh imi v geometricheskih
izmereniyah. Predpolozhim takzhe, chto vrashchayushchayasya platforma zakryta so vseh
storon i predstavlyaet soboj vrashchayushchuyusya komnatu bez okon, chtoby
eksperimentatory ne mogli nablyudat' svoe dvizhenie otnositel'no okruzhayushchih
predmetov. Mogli by v etom sluchae eksperimentatory ob座asnit' vse poluchennye
rezul'taty chisto fizicheskimi usloviyami na platforme bez ucheta ee vrashcheniya
otnositel'no "tverdoj osnovy", na kotoroj ustanovlena platforma?
Glyadya na razlichiya mezhdu fizicheskimi usloviyami na platforme i na
"tverdoj osnove", posredstvom kotoryh mozhno bylo by ob座asnit' nablyudaemye
izmeneniya v geometrii, nashi eksperimentatory srazu zhe zametili by, chto
sushchestvuet kakaya-to novaya sila, kotoraya stremitsya otbrosit' vse tela ot
centra platformy k ee okruzhnosti. Vpolne estestvenno, chto oni pripisali by
nablyudaemye effekty dejstviyu etoj sily, utverzhdaya, naprimer, chto iz dvuh
chasov te budut idti medlennee, kotorye raspolozheny dal'she ot centra v
napravlenii novoj sily.
No dejstvitel'no li eta novaya sila nova, t. e. ne nablyudaema na
"tverdoj osnove"? Razve my ne nablyudaem, kak vse tela prityagivayutsya k centru
Zemli siloj, kotoraya poluchila nazvanie sily tyazhesti? Razumeetsya, v odnom
sluchae my imeem prityazhenie k okruzhnosti diska, v drugom - prityazhenie k
centru Zemli, no eto oznachaet tol'ko razlichie v raspredelenii sily.
Netrudno, odnako, privesti drugoj primer, kogda "novaya" sila, porozhdaemaya
neravnomernym dvizheniem sistemy otscheta, vyglyadit tochno tak zhe, kak sila
tyazhesti v etoj lekcionnoj auditorii.
Predpolozhim, chto kosmicheskij korabl', prednaznachennyj dlya mezhzvezdnyh
pereletov, svobodno letit gde-to v kosmicheskom prostranstve nastol'ko daleko
ot razlichnyh zvezd, chto vnutri korablya sila tyazhesti ne dejstvuet. Vse
predmety vnutri kosmicheskogo korablya i sami puteshestvuyushchie v nem
eksperimentatory nevesomy i svobodno plavayut v vozduhe primerno tak zhe, kak
Mishel' Ardan i ego sputniki vo vremya puteshestviya na Lunu v znamenitom romane
ZHyulya Verna.
No vot dvigateli vklyucheny i kosmicheskij korabl' prihodit v dvizhenie,
postepenno nabiraya skorost'. CHto proishodit vnutri nego? Netrudno videt',
chto poka kosmicheskij korabl' uskoryaetsya, vse predmety vnutri nego
obnaruzhivayut stremlenie dvigat'sya k polu, ili, chto to zhe, pol dvizhetsya
navstrechu etim predmetam. Naprimer, esli nash eksperimentator derzhit v ruke
yabloko i vypuskaet ego, to yabloko prodolzhaet dvigat'sya (otnositel'no
okruzhayushchih korabl' zvezd) s postoyannoj skorost'yu - toj samoj, s kotoroj
dvigalsya kosmicheskij korabl', kogda eksperimentator vypustil iz ruk yabloko.
No kosmicheskij korabl' uskoryaetsya. Sledovatel'no, pol kabiny, dvigayas' vse
bystree i bystree, v konce koncov dogonit yabloko i stuknet ego. S etogo
momenta yabloko ostanetsya v postoyannom kontakte s polom, buduchi prizhato k
polu postoyanno dejstvuyushchim uskoreniem.
No dlya eksperimentatora, nahodyashchegosya vnutri kosmicheskogo korablya, vse
vyglyadit inache: yabloko "padaet" s kakim-to uskoreniem i, udarivshis' ob pol,
ostaetsya lezhat' na polu, pridavlennoe k nemu sobstvennym vesom. Brosaya
razlichnye predmety, nash eksperimentator zametit, chto vse oni padayut s
sovershenno odinakovym uskoreniem (esli prenebrech' treniem o vozduh) i
vspomnit, chto eto - zakon svobodnogo padeniya, otkrytyj Galileo Galileem. _No
nash eksperimentator tak i ne smozhet zametit' ni malejshego razlichiya mezhdu
yavleniyami, proishodyashchimi v dvizhushchejsya s uskoreniem kabine kosmicheskogo
korablya i obychnymi yavleniyami gravitacii. On mozhet pol'zovat'sya mayatnikovymi
chasami, stavit' knigi na polku, ne boyas', chto te uletyat proch', i povesit' na
gvozd' portret Al'berta |jnshtejna, kotoryj pervym ukazal na ekvivalentnost'
uskoreniya sistemy otscheta i gravitacii i na etoj osnove razvil tak
nazyvaemuyu obshchuyu teoriyu otnositel'nosti_.
 No tut, kak i v pervom primere s vrashchayushchejsya platformoj, my zamechaem
yavleniya, ostavshiesya neizvestnymi Galileyu i N'yutonu, kogda te izuchali
gravitaciyu. Luch sveta, poslannyj cherez kabinu, iskrivlyaetsya i osveshchaet v
zavisimosti ot uskoreniya kosmicheskogo korablya kazhdyj raz drugoe mesto
ekrana, visyashchego na protivopolozhnoj stene. Razumeetsya, vneshnij nablyudatel'
interpretiruet eto kak superpoziciyu ravnomernogo pryamolinejnogo dvizheniya
sveta i uskorennogo dvizheniya kabiny, gde proizvodyatsya nablyudeniya. Geometriya
takzhe narushaetsya: summa uglov treugol'nika, obrazovannogo tremya luchami
sveta, budet bol'she dvuh pryamyh uglov, a otnoshenie dliny okruzhnosti k
diametru - bol'she chisla pi. My rassmotreli lish' dva iz prostejshih primerov
uskorenno dvizhushchihsya sistem otscheta, no ustanovlennaya vyshe ekvivalentnost'
ostaetsya v sile dlya lyubogo dvizheniya tverdoj ili deformiruemoj sistemy
otscheta.
Tut my podhodim k voprosu velichajshej vazhnosti. Kak my tol'ko chto
videli, v uskorenno dvizhushchejsya sisteme otscheta mozhet nablyudat'sya ryad
yavlenij, ostavshihsya neizvestnymi dlya obychnogo gravitacionnogo polya.
Sushchestvuyut li eti novye yavleniya, takie kak iskrivlenie lucha sveta ili
zamedlenie chasov, i v gravitacionnyh polyah, porozhdaemyh tyazhelymi massami?
Ili, inache govorya, sushchestvuyut li effekty uskoreniya i effekty gravitacii,
kotorye ne tol'ko ochen' pohozhi, no i tozhdestvenny? Razumeetsya, yasno, chto
hotya s evristicheskoj tochki zreniya ves'ma soblaznitel'no prinyat' polnoe
tozhdestvo etih dvuh raznovidnostej effektov, okonchatel'nyj otvet mozhet byt'
dan tol'ko s pomoshch'yu pryamyh eksperimentov. I k velichajshemu udovletvoreniyu
nashego chelovecheskogo razuma, trebuyushchego prostoty i vnutrennej
neprotivorechivosti zakonov Vselennoj, eksperimenty podtverzhdayut
sushchestvovanie novyh yavlenij, o kotoryh idet rech', i v obychnom gravitacionnom
pole. Razumeetsya, effekty, predskazyvaemye gipotezoj ob ekvivalentnosti
polej uskoreniya i gravitacionnogo polya, ochen' maly. Imenno poetomu oni i
byli otkryty tol'ko posle togo, kak uchenye special'no zanyalis' ih poiskom.
Ispol'zuya privedennyj vyshe primer uskorenno dvizhushchihsya sistem otscheta,
my mozhem legko ocenit' dva naibolee vazhnyh relyativistskih gravitacionnyh
yavleniya po poryadku velichiny: izmenenie skorosti hoda chasov i iskrivlenie
lucha sveta.
Rassmotrim snachala primer s vrashchayushchejsya platformoj. Iz elementarnoj
mehaniki izvestno, chto na chasticu s edinichnoj massoj, raspolozhennuyu na
rasstoyanii r ot centra, dejstvuet centrobezhnaya sila, vychislyaemaya po formule
No tut, kak i v pervom primere s vrashchayushchejsya platformoj, my zamechaem
yavleniya, ostavshiesya neizvestnymi Galileyu i N'yutonu, kogda te izuchali
gravitaciyu. Luch sveta, poslannyj cherez kabinu, iskrivlyaetsya i osveshchaet v
zavisimosti ot uskoreniya kosmicheskogo korablya kazhdyj raz drugoe mesto
ekrana, visyashchego na protivopolozhnoj stene. Razumeetsya, vneshnij nablyudatel'
interpretiruet eto kak superpoziciyu ravnomernogo pryamolinejnogo dvizheniya
sveta i uskorennogo dvizheniya kabiny, gde proizvodyatsya nablyudeniya. Geometriya
takzhe narushaetsya: summa uglov treugol'nika, obrazovannogo tremya luchami
sveta, budet bol'she dvuh pryamyh uglov, a otnoshenie dliny okruzhnosti k
diametru - bol'she chisla pi. My rassmotreli lish' dva iz prostejshih primerov
uskorenno dvizhushchihsya sistem otscheta, no ustanovlennaya vyshe ekvivalentnost'
ostaetsya v sile dlya lyubogo dvizheniya tverdoj ili deformiruemoj sistemy
otscheta.
Tut my podhodim k voprosu velichajshej vazhnosti. Kak my tol'ko chto
videli, v uskorenno dvizhushchejsya sisteme otscheta mozhet nablyudat'sya ryad
yavlenij, ostavshihsya neizvestnymi dlya obychnogo gravitacionnogo polya.
Sushchestvuyut li eti novye yavleniya, takie kak iskrivlenie lucha sveta ili
zamedlenie chasov, i v gravitacionnyh polyah, porozhdaemyh tyazhelymi massami?
Ili, inache govorya, sushchestvuyut li effekty uskoreniya i effekty gravitacii,
kotorye ne tol'ko ochen' pohozhi, no i tozhdestvenny? Razumeetsya, yasno, chto
hotya s evristicheskoj tochki zreniya ves'ma soblaznitel'no prinyat' polnoe
tozhdestvo etih dvuh raznovidnostej effektov, okonchatel'nyj otvet mozhet byt'
dan tol'ko s pomoshch'yu pryamyh eksperimentov. I k velichajshemu udovletvoreniyu
nashego chelovecheskogo razuma, trebuyushchego prostoty i vnutrennej
neprotivorechivosti zakonov Vselennoj, eksperimenty podtverzhdayut
sushchestvovanie novyh yavlenij, o kotoryh idet rech', i v obychnom gravitacionnom
pole. Razumeetsya, effekty, predskazyvaemye gipotezoj ob ekvivalentnosti
polej uskoreniya i gravitacionnogo polya, ochen' maly. Imenno poetomu oni i
byli otkryty tol'ko posle togo, kak uchenye special'no zanyalis' ih poiskom.
Ispol'zuya privedennyj vyshe primer uskorenno dvizhushchihsya sistem otscheta,
my mozhem legko ocenit' dva naibolee vazhnyh relyativistskih gravitacionnyh
yavleniya po poryadku velichiny: izmenenie skorosti hoda chasov i iskrivlenie
lucha sveta.
Rassmotrim snachala primer s vrashchayushchejsya platformoj. Iz elementarnoj
mehaniki izvestno, chto na chasticu s edinichnoj massoj, raspolozhennuyu na
rasstoyanii r ot centra, dejstvuet centrobezhnaya sila, vychislyaemaya po formule
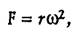 (1)
gde omega - postoyannaya uglovaya skorost' vrashcheniya nashej platformy.
Polnaya rabota, sovershaemaya etoj siloj pri dvizhenii chasticy ot centra do
kraya platformy, ravna velichine
(1)
gde omega - postoyannaya uglovaya skorost' vrashcheniya nashej platformy.
Polnaya rabota, sovershaemaya etoj siloj pri dvizhenii chasticy ot centra do
kraya platformy, ravna velichine
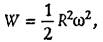 (2)
gde R - radius platformy.
Soglasno sformulirovannomu vyshe principu ekvivalentnosti my dolzhny
otozhdestvit' centrobezhnuyu silu F s siloj tyazhesti na platforme, a rabotu W -
s raznost'yu znachenij gravitacionnogo potenciala v centre i na krayu
platformy.
Napomnim, chto, kak bylo pokazano v predydushchej lekcii, chasy, dvizhushchiesya
so skorost'yu u, zamedlyayut svoj hod v
(2)
gde R - radius platformy.
Soglasno sformulirovannomu vyshe principu ekvivalentnosti my dolzhny
otozhdestvit' centrobezhnuyu silu F s siloj tyazhesti na platforme, a rabotu W -
s raznost'yu znachenij gravitacionnogo potenciala v centre i na krayu
platformy.
Napomnim, chto, kak bylo pokazano v predydushchej lekcii, chasy, dvizhushchiesya
so skorost'yu u, zamedlyayut svoj hod v
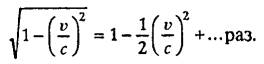 (3)
Esli skorost' u mala po sravneniyu so skorost'yu sveta s, to ostal'nymi
chlenami mozhno prenebrech'. Po opredeleniyu uglovoj skorosti poluchaem r =
R*omega, i "koefficient zamedleniya" mozhno predstavit' v vide
(3)
Esli skorost' u mala po sravneniyu so skorost'yu sveta s, to ostal'nymi
chlenami mozhno prenebrech'. Po opredeleniyu uglovoj skorosti poluchaem r =
R*omega, i "koefficient zamedleniya" mozhno predstavit' v vide
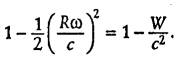 (4)
Formula (4) pokazyvaet, kak izmenyaetsya skorost' hoda chasov v
zavisimosti ot raznosti znachenij gravitacionnogo potenciala v mestah
raspolozheniya chasov.
Esli my pomestim odni chasy u osnovaniya, a drugie - na vershine |jfelevoj
bashni (vysota bashni 300 m), to raznost' znachenij gravitacionnogo potenciala
mezhdu nimi budet tak mala, chto chasy u podnozhiya budut idti medlennee, chem
chasy na vershine bashni, tol'ko v 0,99999999999997 raz.
S drugoj storony, raznost' znachenij gravitacionnogo potenciala mezhdu
poverhnost'yu Zemli i poverhnost'yu Solnca gorazdo bol'she i porozhdaet
koefficient zamedleniya, ravnyj 0,9999995, chto mozhet byt' podtverzhdeno
vysokotochnymi izmereniyami. Razumeetsya, nikto ne sobiraetsya pomeshchat' obychnye
chasy na poverhnost' Solnca i nablyudat' za ih hodom! U fizikov dlya etogo
imeyutsya gorazdo luchshie sredstva. S pomoshch'yu spektroskopa my mozhem nablyudat'
kolebaniya razlichnyh atomov na poverhnosti Solnca i sravnivat' ih s periodami
kolebanij atomov teh zhe elementov, pomeshchennyh v plamya bunzenovskoj gorelki v
laboratorii. Kolebaniya atomov na poverhnosti Solnca dolzhny zamedlyat'sya v
chislo raz, zadavaemoe formuloj (4), i poetomu ispuskaemyj imi svet dolzhen
byt' chut' bolee krasnovatym, chem v sluchae zemnyh istochnikov. Takoe "krasnoe
smeshchenie" dejstvitel'no nablyudaetsya v spektrah Solnca i neskol'kih drugih
zvezd, spektry kotoryh legko poddayutsya izmereniyam, i rezul'taty
eksperimentov soglasuyutsya so znacheniem, kotoroe daet nasha teoreticheskaya
formula.
Takim obrazom, sushchestvovanie krasnogo smeshcheniya dokazalo, chto processy
na Solnce proishodyat dejstvitel'no neskol'ko medlennee, chem na Zemle, iz-za
bolee vysokogo gravitacionnogo potenciala na poverhnosti Solnca.
CHtoby izmerit' kriviznu lucha sveta v gravitacionnom pole, bolee udobno
vospol'zovat'sya primerom s kosmicheskim korablem (s.51). Esli l - rasstoyanie
ot odnoj stenki kabiny do drugoj, to vremya, za kotoroe svet preodolevaet eto
rasstoyanie, opredelyaetsya velichinoj
(4)
Formula (4) pokazyvaet, kak izmenyaetsya skorost' hoda chasov v
zavisimosti ot raznosti znachenij gravitacionnogo potenciala v mestah
raspolozheniya chasov.
Esli my pomestim odni chasy u osnovaniya, a drugie - na vershine |jfelevoj
bashni (vysota bashni 300 m), to raznost' znachenij gravitacionnogo potenciala
mezhdu nimi budet tak mala, chto chasy u podnozhiya budut idti medlennee, chem
chasy na vershine bashni, tol'ko v 0,99999999999997 raz.
S drugoj storony, raznost' znachenij gravitacionnogo potenciala mezhdu
poverhnost'yu Zemli i poverhnost'yu Solnca gorazdo bol'she i porozhdaet
koefficient zamedleniya, ravnyj 0,9999995, chto mozhet byt' podtverzhdeno
vysokotochnymi izmereniyami. Razumeetsya, nikto ne sobiraetsya pomeshchat' obychnye
chasy na poverhnost' Solnca i nablyudat' za ih hodom! U fizikov dlya etogo
imeyutsya gorazdo luchshie sredstva. S pomoshch'yu spektroskopa my mozhem nablyudat'
kolebaniya razlichnyh atomov na poverhnosti Solnca i sravnivat' ih s periodami
kolebanij atomov teh zhe elementov, pomeshchennyh v plamya bunzenovskoj gorelki v
laboratorii. Kolebaniya atomov na poverhnosti Solnca dolzhny zamedlyat'sya v
chislo raz, zadavaemoe formuloj (4), i poetomu ispuskaemyj imi svet dolzhen
byt' chut' bolee krasnovatym, chem v sluchae zemnyh istochnikov. Takoe "krasnoe
smeshchenie" dejstvitel'no nablyudaetsya v spektrah Solnca i neskol'kih drugih
zvezd, spektry kotoryh legko poddayutsya izmereniyam, i rezul'taty
eksperimentov soglasuyutsya so znacheniem, kotoroe daet nasha teoreticheskaya
formula.
Takim obrazom, sushchestvovanie krasnogo smeshcheniya dokazalo, chto processy
na Solnce proishodyat dejstvitel'no neskol'ko medlennee, chem na Zemle, iz-za
bolee vysokogo gravitacionnogo potenciala na poverhnosti Solnca.
CHtoby izmerit' kriviznu lucha sveta v gravitacionnom pole, bolee udobno
vospol'zovat'sya primerom s kosmicheskim korablem (s.51). Esli l - rasstoyanie
ot odnoj stenki kabiny do drugoj, to vremya, za kotoroe svet preodolevaet eto
rasstoyanie, opredelyaetsya velichinoj
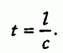 (5)
Za eto vremya kosmicheskij korabl', dvigayas' s uskoreniem g, projdet
rasstoyanie L, velichina kotorogo mozhet byt' vychislena po formule
(5)
Za eto vremya kosmicheskij korabl', dvigayas' s uskoreniem g, projdet
rasstoyanie L, velichina kotorogo mozhet byt' vychislena po formule
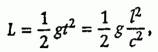 (6)
izvestnoj iz elementarnoj mehaniki. Sledovatel'no, ugol, zadayushchij
izmenenie napravleniya lucha, est' velichina poryadka
(6)
izvestnoj iz elementarnoj mehaniki. Sledovatel'no, ugol, zadayushchij
izmenenie napravleniya lucha, est' velichina poryadka
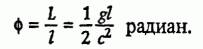 (7)
Ugol f tem bol'she, chem bol'she rasstoyanie l, prohodimoe svetom v
gravitacionnom pole, V formule (7) uskorenie g kosmicheskogo korablya mozhet
byt' interpretirovano kak uskorenie sily tyazhesti. Esli ya posylayu luch sveta
cherez etu auditoriyu, to velichinu l mozhno schitat' primerno ravnoj 1000 sm.
Uskorenie sily tyazhesti g na poverhnosti Zemli sostavlyaet 981 sm/s2, i pri s
= 3 * 10^10 sm/s my poluchaem
(7)
Ugol f tem bol'she, chem bol'she rasstoyanie l, prohodimoe svetom v
gravitacionnom pole, V formule (7) uskorenie g kosmicheskogo korablya mozhet
byt' interpretirovano kak uskorenie sily tyazhesti. Esli ya posylayu luch sveta
cherez etu auditoriyu, to velichinu l mozhno schitat' primerno ravnoj 1000 sm.
Uskorenie sily tyazhesti g na poverhnosti Zemli sostavlyaet 981 sm/s2, i pri s
= 3 * 10^10 sm/s my poluchaem
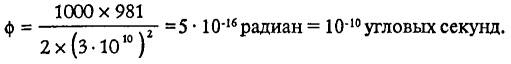 (8)
YAsno, chto pri takih usloviyah nablyudat' kriviznu lucha sveta zavedomo
nevozmozhno. No vblizi poverhnosti Solnca g = 27000 sm/s2, a obshchij put',
prohodimyj svetom v gravitacionnom pole Solnca, ochen' velik. Kak pokazyvayut
tochnye vychisleniya, otklonenie lucha sveta, prohodyashchego vblizi poverhnosti
Solnca, dostigaet velichiny 1,75". Takoe otklonenie nablyudali astronomy po
smeshcheniyu vidimogo polozheniya zvezd vblizi solnechnogo diska vo vremya polnogo
zatmeniya Solnca. Vy vidite, i v etom sluchae nablyudeniya podtverzhdayut
absolyutnoe tozhdestvo effektov uskoreniya i gravitacii.
Teper' my mozhem snova vernut'sya k probleme krivizny prostranstva. Kak
vy pomnite, ispol'zuya naibolee razumnoe opredelenie pryamoj, my prishli k
zaklyucheniyu, chto geometriya, voznikayushchaya v neravnomerno dvizhushchihsya sistemah
otscheta, otlichaetsya ot geometrii Evklida i chto prostranstva s takoj
geometriej sledovalo by schitat' iskrivlennymi. Poskol'ku lyuboe
gravitacionnoe pole ekvivalentno nekotoromu uskoreniyu sistemy otscheta, eto
oznachaet, chto lyuboe prostranstvo s gravitacionnym polem yavlyaetsya
iskrivlennym prostranstvom. Sdelav eshche odin shag vpered, mozhno utverzhdat',
chto _gravitacionnoe pole est' ne chto inoe, kak fizicheskoe proyavlenie
krivizny prostranstva_. Takim obrazom, krivizna v kazhdoj tochke prostranstva
dolzhna opredelyat'sya raspredeleniem mass, i vblizi tyazhelyh tel krivizna
prostranstva dolzhna byt' maksimal'noj. YA ne mogu vdavat'sya zdes' v ves'ma
slozhnuyu matematicheskuyu teoriyu, opisyvayushchuyu svojstva iskrivlennogo
prostranstva i ih zavisimost' ot raspredeleniya mass. Upomyanu tol'ko o tom,
chto krivizna prostranstva, voobshche govorya, opisyvaetsya ne odnim chislom, a
desyat'yu razlichnymi chislami, obshcheizvestnymi pod nazvaniem komponent
gravitacionnogo potenciala g i predstavlyayushchimi soboj obobshchenie
gravitacionnogo polya klassicheskoj fiziki, kotoryj ranee ya oboznachil W.
Sootvetstvenno, krivizna v kazhdoj tochke opisyvaetsya desyat'yu razlichnymi
radiusami krivizny, obychno oboznachaemymi R. |ti radiusy krivizny svyazany s
raspredeleniem mass fundamental'nym uravneniem |jnshtejna
(8)
YAsno, chto pri takih usloviyah nablyudat' kriviznu lucha sveta zavedomo
nevozmozhno. No vblizi poverhnosti Solnca g = 27000 sm/s2, a obshchij put',
prohodimyj svetom v gravitacionnom pole Solnca, ochen' velik. Kak pokazyvayut
tochnye vychisleniya, otklonenie lucha sveta, prohodyashchego vblizi poverhnosti
Solnca, dostigaet velichiny 1,75". Takoe otklonenie nablyudali astronomy po
smeshcheniyu vidimogo polozheniya zvezd vblizi solnechnogo diska vo vremya polnogo
zatmeniya Solnca. Vy vidite, i v etom sluchae nablyudeniya podtverzhdayut
absolyutnoe tozhdestvo effektov uskoreniya i gravitacii.
Teper' my mozhem snova vernut'sya k probleme krivizny prostranstva. Kak
vy pomnite, ispol'zuya naibolee razumnoe opredelenie pryamoj, my prishli k
zaklyucheniyu, chto geometriya, voznikayushchaya v neravnomerno dvizhushchihsya sistemah
otscheta, otlichaetsya ot geometrii Evklida i chto prostranstva s takoj
geometriej sledovalo by schitat' iskrivlennymi. Poskol'ku lyuboe
gravitacionnoe pole ekvivalentno nekotoromu uskoreniyu sistemy otscheta, eto
oznachaet, chto lyuboe prostranstvo s gravitacionnym polem yavlyaetsya
iskrivlennym prostranstvom. Sdelav eshche odin shag vpered, mozhno utverzhdat',
chto _gravitacionnoe pole est' ne chto inoe, kak fizicheskoe proyavlenie
krivizny prostranstva_. Takim obrazom, krivizna v kazhdoj tochke prostranstva
dolzhna opredelyat'sya raspredeleniem mass, i vblizi tyazhelyh tel krivizna
prostranstva dolzhna byt' maksimal'noj. YA ne mogu vdavat'sya zdes' v ves'ma
slozhnuyu matematicheskuyu teoriyu, opisyvayushchuyu svojstva iskrivlennogo
prostranstva i ih zavisimost' ot raspredeleniya mass. Upomyanu tol'ko o tom,
chto krivizna prostranstva, voobshche govorya, opisyvaetsya ne odnim chislom, a
desyat'yu razlichnymi chislami, obshcheizvestnymi pod nazvaniem komponent
gravitacionnogo potenciala g i predstavlyayushchimi soboj obobshchenie
gravitacionnogo polya klassicheskoj fiziki, kotoryj ranee ya oboznachil W.
Sootvetstvenno, krivizna v kazhdoj tochke opisyvaetsya desyat'yu razlichnymi
radiusami krivizny, obychno oboznachaemymi R. |ti radiusy krivizny svyazany s
raspredeleniem mass fundamental'nym uravneniem |jnshtejna
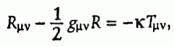 (9)
gde T zavisit ot plotnostej, skorostej i drugih svojstv gravitacionnogo
polya, porozhdaemogo tyazhelymi massami.
V zaklyuchenie lekcii ya hotel by obratit' vashe vnimanie na odno iz
naibolee interesnyh sledstvij iz uravneniya (9). Esli my rassmotrim
prostranstvo, ravnomerno zapolnennoe massami, kak, naprimer, nashe
prostranstvo zapolneno zvezdami i zvezdnymi sistemami, to pridem k
zaklyucheniyu, chto pomimo sluchajno bol'shoj krivizny vblizi otdel'nyh zvezd
prostranstvo dolzhno obladat' _vpolne zakonomernoj tendenciej k ravnomernomu
iskrivleniyu na bol'shih rasstoyaniyah_. S tochki zreniya matematiki sushchestvuet
neskol'ko razlichnyh reshenij fundamental'nogo uravneniya |jnshtejna. Odni iz
nih sootvetstvuyut _prostranstvu, kotoroe zamykaetsya i poetomu obladaet
konechnym ob容mom_, drugie - _beskonechnomu prostranstvu, analogichnomu
sedlovidnoj poverhnosti_, o kotoroj ya upominal v nachale etoj lekcii. Vtoroe
vazhnoe sledstvie iz uravneniya (9) sostoit v tom, chto takie iskrivlennye
prostranstva dolzhny nahodit'sya v sostoyanii neprestannogo rasshireniya ili
szhatiya. Fizicheski eto oznachaet, chto zapolnyayushchie prostranstvo chasticy dolzhny
byli by razletat'sya ili, naoborot, sletat'sya. Krome togo, mozhno pokazat',
chto v sluchae zamknutyh prostranstv s konechnym ob容mom stadii rasshireniya i
szhatiya dolzhny byli by periodicheski cheredovat'sya. Takie prostranstva poluchili
nazvanie pul'siruyushchih vselennyh. S drugoj storony, beskonechnye "sedlovidnye"
prostranstva postoyanno nahodyatsya v sostoyanii szhatiya ili rasshireniya.
Otvet na vopros o tom, kakoe iz etih razlichnyh matematicheski vozmozhnyh
reshenij sootvetstvuet prostranstvu, v kotorom my zhivem, dolzhen byt' najden
ne fizikoj, a astronomiej, i ya ne budu rassmatrivat' ego zdes'. Upomyanu lish'
o tom, chto vse imeyushchiesya astronomicheskie dannye vpolne opredelenno
svidetel'stvuyut o tom, chto nasha Vselennaya rasshiryaetsya, hotya vopros o tom, ne
smenitsya li kogda-nibud' rasshirenie szhatiem, a takzhe o konechnosti ili
beskonechnosti Vselennoj, ostaetsya poka otkrytym.
Pul'siruyushchaya vselennaya
Pervyj vecher svoego prebyvaniya v gostinice "Na beregu Kanala" {Kanal,
ili Anglijskij Kanal, - anglijskoe nazvanie proliva La-Mansh. (Prim. per)}
mister Tompkins zavershil uzhinom v restorane, razumeetsya, v obshchestve starogo
professora i ego ocharovatel'noj docheri. Uzhin udalsya na slavu. Professor bez
umolku razglagol'stvoval o kosmologii, miss Mod premilo boltala ob
iskusstve. Kogda mister Tompkins dobralsya, nakonec, do svoego nomera, on
edva uspel razdet'sya i, bez sil ruhnuv na postel', s golovoj nakrylsya
odeyalom. V ego ustalom mozgu peremeshalis' Bottichelli i Bondi, Sal'vador Dali
i Fred Hojl, Lemetr i Lafonten. Povorochavshis' nekotoroe vremya s boku na bok,
mister Tompkins, nakonec, zabylsya glubokim snom...
Sredi nochi on vdrug prosnulsya ot neozhidannogo oshchushcheniya: emu pokazalos',
chto vmesto myagkogo pruzhinnogo matraca on lezhit na chem-to neobychajno tverdom.
Mister Tompkins otkryl glaza i uvidel sebya prostertym na chem-to,
pokazavshemsya emu snachala skaloj na beregu okeana. Odnako chut' pozzhe on
obnaruzhil, chto dejstvitel'no vozlezhit na skale, metrov etak devyat' v
poperechnike, kotoraya bez vsyakoj vidimoj opory visela v prostranstve. Skala
byla mestami pokryta zelenym mhom, a koe-gde iz rasselin na nej rosli
nebol'shie kustiki. Prostranstvo vokrug skaly bylo osveshcheno kakim-to strannym
mercayushchim svetom i izryadno zabito pyl'yu. Misteru Tompkinsu eshche nikogda ne
prihodilos' videt', chtoby v vozduhe bylo stol'ko pyli, dazhe v fil'mah,
izobrazhavshih pyl'nye buri na Srednem Zapade. On sdelal sebe zashchitnuyu masku
iz nosovogo platka i pochuvstvoval izryadnoe oblegchenie. No v okruzhayushchem
prostranstve byli veshchi i poopasnee pyli. Ochen' chasto kamni razmerom s golovu
mistera Tompkinsa i pobolee pronosilis' v prostranstve u samoj skaly i vremya
ot vremeni vrezalis' v nee s neprivychno gluhim stukom. No i eto eshche ne vse:
obozrevaya okrestnosti, misteru Tompkinsu prihodilos' izo vseh sil ceplyat'sya
za vystupy skaly i prizhimat'sya k nej, opasayas' sorvat'sya so skaly i sginut'
v pyl'noj bezdne. No vskore mister Tompkins nabralsya hrabrosti i popytalsya
vzobrat'sya na kraj skaly, chtoby ubedit'sya v tom, chto pod nej dejstvitel'no
net nikakoj opory. Podpolzaya k krayu skaly, mister Tompkins k svoemu velikomu
udivleniyu zametil, chto ne padaet so skaly. Naoborot, ego ves postoyanno
prizhimaet ego k poverhnosti skaly, hotya sama skala nevelika i on uspel
propolzti uzhe ne menee chetverti ee ohvata. Vzglyanuv iz-za grudy kamnej na to
mesto, kotoroe raspolozheno v akkurat pod tem mestom, gde mister Tompkins
pervonachal'no okazalsya, on ubedilsya, chto skala svobodno visit v prostranstve
i ee nichto ne podderzhivaet. K svoemu velikomu izumleniyu, mister Tompkins
vnezapno uvidel v mercayushchem svete svoego druga - starogo professora,
stoyavshego na skale, kak pokazalos' misteru Tompkinsu, vniz golovoj i
delavshego kakie-to zametki v zapisnoj knizhke.
Teper' do mistera Tompkinsa medlenno stalo dohodit', chto proishodit. On
vspomnil, kak v detstve uchil v shkole, chto Zemlya - ogromnaya kruglaya skala,
svobodno obrashchayushchayasya v kosmicheskom prostranstve vokrug Solnca. Mister
Tompkins vspomnil takzhe risunok iz shkol'nogo uchebnika: dva antipoda, stoyashchie
na protivopolozhnyh storonah Zemli. Nu konechno zhe! Ego skala byla nebesnym
telom ochen' malyh razmerov, prityagivavshim vse k svoej poverhnosti, a on sam
i staryj professor sostavlyali vse naselenie etoj krohotnoj planety.
Razmyshleniya neskol'ko uteshili mistera Tompkinsa: po krajnej mere ne bylo
opasnosti svalit'sya so skaly v kosmicheskoe prostranstvo!
- Dobroe utro, - proiznes mister Tompkins, chtoby otvlech' vnimanie
starogo professora ot vychislenij, v kotorye tot ushel s golovoj.
(9)
gde T zavisit ot plotnostej, skorostej i drugih svojstv gravitacionnogo
polya, porozhdaemogo tyazhelymi massami.
V zaklyuchenie lekcii ya hotel by obratit' vashe vnimanie na odno iz
naibolee interesnyh sledstvij iz uravneniya (9). Esli my rassmotrim
prostranstvo, ravnomerno zapolnennoe massami, kak, naprimer, nashe
prostranstvo zapolneno zvezdami i zvezdnymi sistemami, to pridem k
zaklyucheniyu, chto pomimo sluchajno bol'shoj krivizny vblizi otdel'nyh zvezd
prostranstvo dolzhno obladat' _vpolne zakonomernoj tendenciej k ravnomernomu
iskrivleniyu na bol'shih rasstoyaniyah_. S tochki zreniya matematiki sushchestvuet
neskol'ko razlichnyh reshenij fundamental'nogo uravneniya |jnshtejna. Odni iz
nih sootvetstvuyut _prostranstvu, kotoroe zamykaetsya i poetomu obladaet
konechnym ob容mom_, drugie - _beskonechnomu prostranstvu, analogichnomu
sedlovidnoj poverhnosti_, o kotoroj ya upominal v nachale etoj lekcii. Vtoroe
vazhnoe sledstvie iz uravneniya (9) sostoit v tom, chto takie iskrivlennye
prostranstva dolzhny nahodit'sya v sostoyanii neprestannogo rasshireniya ili
szhatiya. Fizicheski eto oznachaet, chto zapolnyayushchie prostranstvo chasticy dolzhny
byli by razletat'sya ili, naoborot, sletat'sya. Krome togo, mozhno pokazat',
chto v sluchae zamknutyh prostranstv s konechnym ob容mom stadii rasshireniya i
szhatiya dolzhny byli by periodicheski cheredovat'sya. Takie prostranstva poluchili
nazvanie pul'siruyushchih vselennyh. S drugoj storony, beskonechnye "sedlovidnye"
prostranstva postoyanno nahodyatsya v sostoyanii szhatiya ili rasshireniya.
Otvet na vopros o tom, kakoe iz etih razlichnyh matematicheski vozmozhnyh
reshenij sootvetstvuet prostranstvu, v kotorom my zhivem, dolzhen byt' najden
ne fizikoj, a astronomiej, i ya ne budu rassmatrivat' ego zdes'. Upomyanu lish'
o tom, chto vse imeyushchiesya astronomicheskie dannye vpolne opredelenno
svidetel'stvuyut o tom, chto nasha Vselennaya rasshiryaetsya, hotya vopros o tom, ne
smenitsya li kogda-nibud' rasshirenie szhatiem, a takzhe o konechnosti ili
beskonechnosti Vselennoj, ostaetsya poka otkrytym.
Pul'siruyushchaya vselennaya
Pervyj vecher svoego prebyvaniya v gostinice "Na beregu Kanala" {Kanal,
ili Anglijskij Kanal, - anglijskoe nazvanie proliva La-Mansh. (Prim. per)}
mister Tompkins zavershil uzhinom v restorane, razumeetsya, v obshchestve starogo
professora i ego ocharovatel'noj docheri. Uzhin udalsya na slavu. Professor bez
umolku razglagol'stvoval o kosmologii, miss Mod premilo boltala ob
iskusstve. Kogda mister Tompkins dobralsya, nakonec, do svoego nomera, on
edva uspel razdet'sya i, bez sil ruhnuv na postel', s golovoj nakrylsya
odeyalom. V ego ustalom mozgu peremeshalis' Bottichelli i Bondi, Sal'vador Dali
i Fred Hojl, Lemetr i Lafonten. Povorochavshis' nekotoroe vremya s boku na bok,
mister Tompkins, nakonec, zabylsya glubokim snom...
Sredi nochi on vdrug prosnulsya ot neozhidannogo oshchushcheniya: emu pokazalos',
chto vmesto myagkogo pruzhinnogo matraca on lezhit na chem-to neobychajno tverdom.
Mister Tompkins otkryl glaza i uvidel sebya prostertym na chem-to,
pokazavshemsya emu snachala skaloj na beregu okeana. Odnako chut' pozzhe on
obnaruzhil, chto dejstvitel'no vozlezhit na skale, metrov etak devyat' v
poperechnike, kotoraya bez vsyakoj vidimoj opory visela v prostranstve. Skala
byla mestami pokryta zelenym mhom, a koe-gde iz rasselin na nej rosli
nebol'shie kustiki. Prostranstvo vokrug skaly bylo osveshcheno kakim-to strannym
mercayushchim svetom i izryadno zabito pyl'yu. Misteru Tompkinsu eshche nikogda ne
prihodilos' videt', chtoby v vozduhe bylo stol'ko pyli, dazhe v fil'mah,
izobrazhavshih pyl'nye buri na Srednem Zapade. On sdelal sebe zashchitnuyu masku
iz nosovogo platka i pochuvstvoval izryadnoe oblegchenie. No v okruzhayushchem
prostranstve byli veshchi i poopasnee pyli. Ochen' chasto kamni razmerom s golovu
mistera Tompkinsa i pobolee pronosilis' v prostranstve u samoj skaly i vremya
ot vremeni vrezalis' v nee s neprivychno gluhim stukom. No i eto eshche ne vse:
obozrevaya okrestnosti, misteru Tompkinsu prihodilos' izo vseh sil ceplyat'sya
za vystupy skaly i prizhimat'sya k nej, opasayas' sorvat'sya so skaly i sginut'
v pyl'noj bezdne. No vskore mister Tompkins nabralsya hrabrosti i popytalsya
vzobrat'sya na kraj skaly, chtoby ubedit'sya v tom, chto pod nej dejstvitel'no
net nikakoj opory. Podpolzaya k krayu skaly, mister Tompkins k svoemu velikomu
udivleniyu zametil, chto ne padaet so skaly. Naoborot, ego ves postoyanno
prizhimaet ego k poverhnosti skaly, hotya sama skala nevelika i on uspel
propolzti uzhe ne menee chetverti ee ohvata. Vzglyanuv iz-za grudy kamnej na to
mesto, kotoroe raspolozheno v akkurat pod tem mestom, gde mister Tompkins
pervonachal'no okazalsya, on ubedilsya, chto skala svobodno visit v prostranstve
i ee nichto ne podderzhivaet. K svoemu velikomu izumleniyu, mister Tompkins
vnezapno uvidel v mercayushchem svete svoego druga - starogo professora,
stoyavshego na skale, kak pokazalos' misteru Tompkinsu, vniz golovoj i
delavshego kakie-to zametki v zapisnoj knizhke.
Teper' do mistera Tompkinsa medlenno stalo dohodit', chto proishodit. On
vspomnil, kak v detstve uchil v shkole, chto Zemlya - ogromnaya kruglaya skala,
svobodno obrashchayushchayasya v kosmicheskom prostranstve vokrug Solnca. Mister
Tompkins vspomnil takzhe risunok iz shkol'nogo uchebnika: dva antipoda, stoyashchie
na protivopolozhnyh storonah Zemli. Nu konechno zhe! Ego skala byla nebesnym
telom ochen' malyh razmerov, prityagivavshim vse k svoej poverhnosti, a on sam
i staryj professor sostavlyali vse naselenie etoj krohotnoj planety.
Razmyshleniya neskol'ko uteshili mistera Tompkinsa: po krajnej mere ne bylo
opasnosti svalit'sya so skaly v kosmicheskoe prostranstvo!
- Dobroe utro, - proiznes mister Tompkins, chtoby otvlech' vnimanie
starogo professora ot vychislenij, v kotorye tot ushel s golovoj.
 Professor otorval glaza ot zapisnoj knizhki.
- Zdes' net nikakih utr, - skazal on, - net Solnca, kak net ni odnoj
svetyashchejsya zvezdy vo vsej etoj vselennoj. Horosho eshche, chto na poverhnosti tel
zdes' ne protekayut koe-kakie himicheskie processy, inache ya prosto ne smog by
nablyudat' za rasshireniem etogo uchastka vselennoj. - I s etimi slovami
professor snova utknulsya v svoyu zapisnuyu knizhku.
Mister Tompkins ochen' rasstroilsya: podumat' tol'ko, vstretit'
edinstvennoe zhivoe sushchestvo vo vsej vselennoj i obnaruzhit', chto ono tak
neobshchitel'no! Neozhidanno misteru Tompkinsu na pomoshch' prishel odin iz melkih
meteoritov: so stukom udarivshis' o zapisnuyu knizhku, on vybil ee iz ruk
professora i unes ee v kosmicheskie dali, proch' ot malen'koj planety.
- Bol'she vy ee ne uvidite, - zametil mister Tompkins, glyadya, kak
zapisnaya knizhka, stanovyas' vse men'she i men'she, skrylas' iz vidu.
- Naoborot! - zhivo vozrazil professor. - Vidite li, prostranstvo, gde
my s vami nahodimsya, imeet ne beskonechnuyu protyazhennost'. O da, da! YA znayu,
chto v shkole vas uchili, budto prostranstvo beskonechno i dve parallel'nye
pryamye nikogda ne peresekayutsya. No eto neverno ni dlya prostranstva, v
kotorom obitaet ostal'noe chelovechestvo, ni dlya prostranstva, v kotorom
nahodimsya sejchas my s vami. Razumeetsya, prostranstvo, v kotorom zhivet vse
ostal'noe chelovechestvo, ochen' veliko, i, po ocenkam uchenyh, prostiraetsya
primerno na 10000000000000000000000 kilometrov, chto dlya zauryadnogo uma
vpolne mozhet sojti za beskonechnost'. Esli by ya poteryal svoyu zapisnuyu knizhku
v toj Vselennoj, to zhdat' by ee prishlos' neveroyatno dolgo. Zdes' zhe, gde my
s vami nahodimsya, situaciya sovershenno inaya. Kak raz pered tem, kak zapisnaya
knizhka byla stol' neozhidanno vyrvana iz moih ruk, ya podschital, chto eto
prostranstvo imeet poperechnik vsego lish' okolo desyati kilometrov, hotya i
bystro rasshiryaetsya. Dumayu, chto moya zapisnaya knizhka vernetsya primerno cherez
polchasa.
- Vy polagaete, - robko podal golos mister Tompkins, - chto vasha
zapisnaya knizhka povedet sebya, kak bumerang aborigenov Avstralii, i, opisav
iskrivlennuyu traektoriyu, upadet k vashim nogam?
- Nichego podobnogo, - vozrazil professor. - Esli hotite ponyat', chto
proizojdet v dejstvitel'nosti, podumajte o kakom-nibud' drevnem greke,
kotoryj ne znal, chto Zemlya kruglaya. Predpolozhim, chto nash grek otdal
komu-nibud' instrukcii dvigat'sya vse vremya na sever. Predstav'te sebe ego
izumlenie, kogda poslanec vernetsya k nemu s yuga. Ved' nash drevnij grek ne
imeet ni malejshego ponyatiya o krugosvetnom puteshestvii (govorya o puteshestvii
vokrug sveta, ya, konechno, imeyu v vidu puteshestvie vokrug Zemli) i budet
prebyvat' v polnoj uverennosti, chto poslanec sbilsya s istinnogo puti i,
opisav iskrivlennyj marshrut, vernulsya v ishodnuyu tochku. V dejstvitel'nosti
zhe ego poslanec vse vremya dvigalsya po kratchajshej linii, kakuyu tol'ko mozhno
provesti na poverhnosti Zemli, no, obojdya vokrug zemnogo shara, vernulsya v
ishodnuyu tochku s protivopolozhnoj storony. To zhe samoe proizojdet i s moej
zapisnoj knizhkoj, esli tol'ko po doroge ona ne stolknetsya s kakim-nibud'
kamnem i ne otklonitsya ot pravil'nogo puti. Vot, voz'mite etot binokl'.
Mozhet byt', vam udastsya razglyadet' ee.
Mister Tompkins podnes k glazam binokl' i, hotya pyl' neskol'ko
zatemnyala obshchuyu kartinu, dejstvitel'no razglyadel zapisnuyu knizhku professora,
plyvushchuyu daleko ot nih v glubine kosmicheskogo prostranstva. Mistera
Tompkinsa neskol'ko udivilo, chto vse dalekie predmety, v tom chisle i
zapisnaya knizhka, imeyut rozovyj cvet.
- Vasha zapisnaya knizhka vozvrashchaetsya, - voskliknul on chut' pozzhe, - ya
vizhu, kak ona uvelichivaetsya v razmerah.
- Net, - otkliknulsya professor, - ona vse eshche udalyaetsya ot nas. To, chto
vy vidite, kak ona uvelichivaetsya v razmerah, ob座asnyaetsya osobym fokusiruyushchim
dejstviem zamknutogo sfericheskogo prostranstva na luchi sveta. Vernemsya k
nashemu drevnemu greku. Esli by luchi sveta, naprimer s pomoshch'yu atmosfernoj
refrakcii, mozhno bylo zastavit' rasprostranyat'sya vdol' iskrivlennoj
poverhnosti Zemli, to nash grek, bud' u nego moshchnyj binokl', mog by sledit'
za svoim poslancem na protyazhenii vsego puteshestviya. Vzglyanuv na globus, vy
zametite, chto pryamejshie linii na ego poverhnosti - meridiany - snachala
rashodyatsya ot odnogo polyusa, no posle prohozhdeniya cherez ekvator nachinayut
shodit'sya k protivopolozhnomu polyusu. Esli by luchi sveta rasprostranyalis'
vdol' meridianov, to vy nahodyas', naprimer, na odnom polyuse, uvideli, kak
poslanec, udalyayas' ot vas, umen'shaetsya v razmerah tol'ko do teh por, poka ne
peresechet ekvator. Zatem vy uvidite, kak on uvelichivaetsya v razmerah, i vam
budet kazat'sya, chto on vozvrashchaetsya, togda kak v dejstvitel'nosti on budet
dvigat'sya vse dal'she i dal'she ot vas. Kogda poslanec dostignet
protivopolozhnogo polyusa, vy uvidite ego v natural'nuyu velichinu - takim, kak
esli by on stoyal ryadom s vami. Odnako vy ne mogli by kosnut'sya ego, kak ne
mogli by potrogat' izobrazhenie v sfericheskom zerkale. Opirayas' na etu
dvumernuyu analogiyu, vy mozhete teper' predstavit', chto proizojdet s luchami
sveta v neobychno iskrivlennom trehmernom prostranstve.
- Vzglyanite, - prerval sebya na poluslove professor, - izobrazhenie moej
zapisnoj knizhki sovsem ryadom.
Dejstvitel'no, bez vsyakogo binoklya mister Tompkins mog videt', chto
zapisnaya knizhka nahodilas' ne bolee chem v metre ot nih. No vyglyadela ona
ves'ma stranno! Kontury ee byli ne rezkimi, a sil'no razmytymi, formuly,
kotorymi professor ispisal stranichki, byli edva razlichimy, a vsya zapisnaya
knizhka v celom vyglyadela, kak fotografiya, snyataya ne v fokuse i k tomu zhe eshche
nedoproyavlennaya.
- Teper' vy sami mozhete ubedit'sya, - zametil professor, - chto pered
vami ne sama zapisnaya knizhka, a vsego lish' ee izobrazhenie, sil'no iskazhennoe
svetom, kotoromu prishlos' projti polmira. Esli hotite okonchatel'no ubedit'sya
v tom, chto pered vami izobrazhenie, vzglyanite v stranicy povnimatel'nee i vy
uvidite skvoz' nih kamni, letyashchie v kosmicheskom prostranstve za knizhkoj.
Mister Tomkins popytalsya bylo shvatit' zapisnuyu knizhku, no ruka ego bez
vsyakogo soprotivleniya proshla skvoz' izobrazhenie.
- Sama zapisnaya knizhka, - prodolzhal professor, - nahoditsya sejchas ochen'
blizko ot protivopolozhnogo polyusa vselennoj. Vtoroe izobrazhenie knizhki
sejchas pryamo u vas za spinoj, i kogda oba izobrazheniya sovpadut, nastoyashchaya
knizhka okazhetsya na protivopolozhnom polyuse.
No mister Tompkins uzhe nichego ne slyshal. On gluboko pogruzilsya v
razmyshleniya, pytayas' pripomnit', kak stroyatsya izobrazheniya ob容ktov v
elementarnoj optike s pomoshch'yu vognutyh zerkal i linz. Kogda mister Tompkins
ochnulsya, izobrazheniya snova rashodilis' v protivopolozhnye storony.
- A chto iskrivlyaet prostranstvo i porozhdaet vse eti zabavnye effekty? -
sprosil mister Tompkins professora.
- Nalichie tyazheloj materii, - posledoval otvet. - Kogda N'yuton otkryl
zakon vsemirnogo tyagoteniya, on videl v gravitacii obychnuyu silu, takuyu zhe,
kak, naprimer, sila, porozhdaemaya uprugoj nit'yu, natyanutoj mezhdu dvumya
telami. Odnako vsegda ostaetsya zagadkoj to obstoyatel'stvo, chto vse tela
nezavisimo ot ih massy i razmera obladayut odnim i tem zhe uskoreniem i, esli
isklyuchit' soprotivlenie vozduha i tomu podobnye effekty, pod dejstviem sil
tyagoteniya dvizhutsya odinakovo. |jnshtejn pervym yasno i opredelenno pokazal,
chto tyazhelaya materiya prezhde vsego porozhdaet kriviznu prostranstva i chto
traektorii vseh tel, dvizhushchihsya v gravitacionnom pole, iskrivleny tol'ko
potomu, chto iskrivleno samo prostranstvo. Boyus' odnako, chto vam bez
dostatochnoj matematicheskoj podgotovki trudno razobrat'sya vo vsem etom.
- Nelegko, - soglasilsya mister Tompkins. - No skazhite mne, pozhalujsta,
byla by u nas ta geometriya, kotoroj menya uchili v shkole, esli by materii
voobshche ne bylo, i peresekalis' by togda parallel'nye pryamye?
- Parallel'nye ne peresekalis' by, - podtverdil professor, - no ni odno
material'noe sushchestvo ne moglo by proverit' eto.
- Mozhet byt', nikakogo Evklida v dejstvitel'nosti ne bylo i poetomu on
ne mog sozdat' geometriyu absolyutno pustogo prostranstva?
No professor yavno ne zhelal vdavat'sya v metafizicheskuyu diskussiyu.
Mezhdu tem izobrazhenie zapisnoj knizhki udalilos' v pervonachal'nom
napravlenii i nachalo priblizhat'sya vo vtoroj raz. Teper' ono bylo iskazheno
eshche bol'she, chem prezhde, i uznat' v nem "prizrak" zapisnoj knizhki bylo pochti
nevozmozhno. Po mneniyu professora, stol' sil'noe iskazhenie ob座asnyalos' tem,
chto lucham sveta na etot raz prihodilos' obhodit' ves' mir.
- Esli vy eshche raz oglyanetes', - obratilsya professor k misteru
Tompkinsu, - to uvidite moyu zapisnuyu knizhku, kotoraya, nakonec, vozvrashchaetsya
ko mne, sovershiv krugosvetnoe puteshestvie.
Professor protyanul ruku, pojmal zapisnuyu knizhku i zasunul ee v karman.
- V etoj vselennoj, kak vy mozhete ubedit'sya sami, tak mnogo pyli i
kamnej, - skazal professor, - chto pochti nevozmozhno okinut' vzglyadom ves'
mir. |ti besformennye teni, kotorye vy vidite vokrug nas, skoree vsego nashi
izobrazheniya i izobrazheniya okruzhayushchih predmetov. Odnako oni tak sil'no
iskazheny pyl'yu i defektami krivizny prostranstva, chto ya ne berus' skazat',
chemu sootvetstvuet kazhdoe takoe izobrazhenie.
- A ne nablyudaetsya li takoj zhe effekt v bol'shoj Vselennoj, gde my s
vami zhili ran'she? - sprosil mister Tompkins.
- Konechno, nablyudaetsya, - posledoval otvet, - no ta Vselennaya nastol'ko
velika, chto svetu trebuyutsya milliardy let, chtoby obojti ee. Vy mogli by, ne
pol'zuyas' zerkalom, uvidet', kak parikmaher postrig vas szadi, no lish' cherez
milliardy let posle togo, kak pobyvaete u parikmahera. Krome togo, veroyatnee
vsego mezhzvezdnaya pyl' polnost'yu zatemnit izobrazhenie. Kstati skazat', odin
anglijskij astronom predpolozhil dazhe kak-to raz, skoree v shutku, chem
vser'ez, chto vidimye sejchas zvezdy na nebe - ne bolee chem izobrazheniya zvezd,
sushchestvovavshih v ochen' dalekuyu epohu.
Ustav ot usilij ponyat' vse eti ob座asneniya, mister Tompkins oglyanulsya i
k svoemu bol'shomu udivleniyu zametil, chto kartina neba znachitel'no
izmenilas'. Pyli stalo zametno men'she, i on snyal s lica masku, kotoruyu
smasteril iz nosovogo platka. Nebol'shie kameshki proletali znachitel'no rezhe i
stukalis' o poverhnost' skaly s gorazdo men'shej energiej. CHto zhe kasaetsya
neskol'kih bol'shih skal, napodobie toj, na kotoroj nashli priyut i on sam,
mister Tompkins, i staryj professor, to teper' bol'shie skaly ne mayachili
poblizosti, kak v samom nachale, a udalilis' na bol'shie rasstoyaniya drug ot
druga i stali edva razlichimymi.
- ZHizn' yavno idet na lad, - podumal mister Tompkins, - a to ya vse
opasalsya, kak by odin iz etih bluzhdayushchih kamnej ne vrezalsya v menya.
- Mozhete li vy ob座asnit' izmeneniya, proishodyashchie vokrug nas? - sprosil
on, povernuvshis' k professoru.
- Ochen' dazhe prosto, - s gotovnost'yu otvetil tot. - Nasha malen'kaya
vselennaya ochen' bystro rasshiryaetsya i s teh por, kak my zdes' okazalis', ee
razmery uvelichilis' s desyati do primerno sotni kilometrov. Kak tol'ko ya
zdes' ochutilsya, rasshirenie bylo mne zametno po pokrasneniyu dalekih ob容ktov.
- YA tozhe zametil, chto na bol'shom rasstoyanii vse stanovitsya rozovym, -
podtverdil mister Tompkins, - no pochemu eto svidetel'stvuet o rasshirenii
vselennoj?
Professor otorval glaza ot zapisnoj knizhki.
- Zdes' net nikakih utr, - skazal on, - net Solnca, kak net ni odnoj
svetyashchejsya zvezdy vo vsej etoj vselennoj. Horosho eshche, chto na poverhnosti tel
zdes' ne protekayut koe-kakie himicheskie processy, inache ya prosto ne smog by
nablyudat' za rasshireniem etogo uchastka vselennoj. - I s etimi slovami
professor snova utknulsya v svoyu zapisnuyu knizhku.
Mister Tompkins ochen' rasstroilsya: podumat' tol'ko, vstretit'
edinstvennoe zhivoe sushchestvo vo vsej vselennoj i obnaruzhit', chto ono tak
neobshchitel'no! Neozhidanno misteru Tompkinsu na pomoshch' prishel odin iz melkih
meteoritov: so stukom udarivshis' o zapisnuyu knizhku, on vybil ee iz ruk
professora i unes ee v kosmicheskie dali, proch' ot malen'koj planety.
- Bol'she vy ee ne uvidite, - zametil mister Tompkins, glyadya, kak
zapisnaya knizhka, stanovyas' vse men'she i men'she, skrylas' iz vidu.
- Naoborot! - zhivo vozrazil professor. - Vidite li, prostranstvo, gde
my s vami nahodimsya, imeet ne beskonechnuyu protyazhennost'. O da, da! YA znayu,
chto v shkole vas uchili, budto prostranstvo beskonechno i dve parallel'nye
pryamye nikogda ne peresekayutsya. No eto neverno ni dlya prostranstva, v
kotorom obitaet ostal'noe chelovechestvo, ni dlya prostranstva, v kotorom
nahodimsya sejchas my s vami. Razumeetsya, prostranstvo, v kotorom zhivet vse
ostal'noe chelovechestvo, ochen' veliko, i, po ocenkam uchenyh, prostiraetsya
primerno na 10000000000000000000000 kilometrov, chto dlya zauryadnogo uma
vpolne mozhet sojti za beskonechnost'. Esli by ya poteryal svoyu zapisnuyu knizhku
v toj Vselennoj, to zhdat' by ee prishlos' neveroyatno dolgo. Zdes' zhe, gde my
s vami nahodimsya, situaciya sovershenno inaya. Kak raz pered tem, kak zapisnaya
knizhka byla stol' neozhidanno vyrvana iz moih ruk, ya podschital, chto eto
prostranstvo imeet poperechnik vsego lish' okolo desyati kilometrov, hotya i
bystro rasshiryaetsya. Dumayu, chto moya zapisnaya knizhka vernetsya primerno cherez
polchasa.
- Vy polagaete, - robko podal golos mister Tompkins, - chto vasha
zapisnaya knizhka povedet sebya, kak bumerang aborigenov Avstralii, i, opisav
iskrivlennuyu traektoriyu, upadet k vashim nogam?
- Nichego podobnogo, - vozrazil professor. - Esli hotite ponyat', chto
proizojdet v dejstvitel'nosti, podumajte o kakom-nibud' drevnem greke,
kotoryj ne znal, chto Zemlya kruglaya. Predpolozhim, chto nash grek otdal
komu-nibud' instrukcii dvigat'sya vse vremya na sever. Predstav'te sebe ego
izumlenie, kogda poslanec vernetsya k nemu s yuga. Ved' nash drevnij grek ne
imeet ni malejshego ponyatiya o krugosvetnom puteshestvii (govorya o puteshestvii
vokrug sveta, ya, konechno, imeyu v vidu puteshestvie vokrug Zemli) i budet
prebyvat' v polnoj uverennosti, chto poslanec sbilsya s istinnogo puti i,
opisav iskrivlennyj marshrut, vernulsya v ishodnuyu tochku. V dejstvitel'nosti
zhe ego poslanec vse vremya dvigalsya po kratchajshej linii, kakuyu tol'ko mozhno
provesti na poverhnosti Zemli, no, obojdya vokrug zemnogo shara, vernulsya v
ishodnuyu tochku s protivopolozhnoj storony. To zhe samoe proizojdet i s moej
zapisnoj knizhkoj, esli tol'ko po doroge ona ne stolknetsya s kakim-nibud'
kamnem i ne otklonitsya ot pravil'nogo puti. Vot, voz'mite etot binokl'.
Mozhet byt', vam udastsya razglyadet' ee.
Mister Tompkins podnes k glazam binokl' i, hotya pyl' neskol'ko
zatemnyala obshchuyu kartinu, dejstvitel'no razglyadel zapisnuyu knizhku professora,
plyvushchuyu daleko ot nih v glubine kosmicheskogo prostranstva. Mistera
Tompkinsa neskol'ko udivilo, chto vse dalekie predmety, v tom chisle i
zapisnaya knizhka, imeyut rozovyj cvet.
- Vasha zapisnaya knizhka vozvrashchaetsya, - voskliknul on chut' pozzhe, - ya
vizhu, kak ona uvelichivaetsya v razmerah.
- Net, - otkliknulsya professor, - ona vse eshche udalyaetsya ot nas. To, chto
vy vidite, kak ona uvelichivaetsya v razmerah, ob座asnyaetsya osobym fokusiruyushchim
dejstviem zamknutogo sfericheskogo prostranstva na luchi sveta. Vernemsya k
nashemu drevnemu greku. Esli by luchi sveta, naprimer s pomoshch'yu atmosfernoj
refrakcii, mozhno bylo zastavit' rasprostranyat'sya vdol' iskrivlennoj
poverhnosti Zemli, to nash grek, bud' u nego moshchnyj binokl', mog by sledit'
za svoim poslancem na protyazhenii vsego puteshestviya. Vzglyanuv na globus, vy
zametite, chto pryamejshie linii na ego poverhnosti - meridiany - snachala
rashodyatsya ot odnogo polyusa, no posle prohozhdeniya cherez ekvator nachinayut
shodit'sya k protivopolozhnomu polyusu. Esli by luchi sveta rasprostranyalis'
vdol' meridianov, to vy nahodyas', naprimer, na odnom polyuse, uvideli, kak
poslanec, udalyayas' ot vas, umen'shaetsya v razmerah tol'ko do teh por, poka ne
peresechet ekvator. Zatem vy uvidite, kak on uvelichivaetsya v razmerah, i vam
budet kazat'sya, chto on vozvrashchaetsya, togda kak v dejstvitel'nosti on budet
dvigat'sya vse dal'she i dal'she ot vas. Kogda poslanec dostignet
protivopolozhnogo polyusa, vy uvidite ego v natural'nuyu velichinu - takim, kak
esli by on stoyal ryadom s vami. Odnako vy ne mogli by kosnut'sya ego, kak ne
mogli by potrogat' izobrazhenie v sfericheskom zerkale. Opirayas' na etu
dvumernuyu analogiyu, vy mozhete teper' predstavit', chto proizojdet s luchami
sveta v neobychno iskrivlennom trehmernom prostranstve.
- Vzglyanite, - prerval sebya na poluslove professor, - izobrazhenie moej
zapisnoj knizhki sovsem ryadom.
Dejstvitel'no, bez vsyakogo binoklya mister Tompkins mog videt', chto
zapisnaya knizhka nahodilas' ne bolee chem v metre ot nih. No vyglyadela ona
ves'ma stranno! Kontury ee byli ne rezkimi, a sil'no razmytymi, formuly,
kotorymi professor ispisal stranichki, byli edva razlichimy, a vsya zapisnaya
knizhka v celom vyglyadela, kak fotografiya, snyataya ne v fokuse i k tomu zhe eshche
nedoproyavlennaya.
- Teper' vy sami mozhete ubedit'sya, - zametil professor, - chto pered
vami ne sama zapisnaya knizhka, a vsego lish' ee izobrazhenie, sil'no iskazhennoe
svetom, kotoromu prishlos' projti polmira. Esli hotite okonchatel'no ubedit'sya
v tom, chto pered vami izobrazhenie, vzglyanite v stranicy povnimatel'nee i vy
uvidite skvoz' nih kamni, letyashchie v kosmicheskom prostranstve za knizhkoj.
Mister Tomkins popytalsya bylo shvatit' zapisnuyu knizhku, no ruka ego bez
vsyakogo soprotivleniya proshla skvoz' izobrazhenie.
- Sama zapisnaya knizhka, - prodolzhal professor, - nahoditsya sejchas ochen'
blizko ot protivopolozhnogo polyusa vselennoj. Vtoroe izobrazhenie knizhki
sejchas pryamo u vas za spinoj, i kogda oba izobrazheniya sovpadut, nastoyashchaya
knizhka okazhetsya na protivopolozhnom polyuse.
No mister Tompkins uzhe nichego ne slyshal. On gluboko pogruzilsya v
razmyshleniya, pytayas' pripomnit', kak stroyatsya izobrazheniya ob容ktov v
elementarnoj optike s pomoshch'yu vognutyh zerkal i linz. Kogda mister Tompkins
ochnulsya, izobrazheniya snova rashodilis' v protivopolozhnye storony.
- A chto iskrivlyaet prostranstvo i porozhdaet vse eti zabavnye effekty? -
sprosil mister Tompkins professora.
- Nalichie tyazheloj materii, - posledoval otvet. - Kogda N'yuton otkryl
zakon vsemirnogo tyagoteniya, on videl v gravitacii obychnuyu silu, takuyu zhe,
kak, naprimer, sila, porozhdaemaya uprugoj nit'yu, natyanutoj mezhdu dvumya
telami. Odnako vsegda ostaetsya zagadkoj to obstoyatel'stvo, chto vse tela
nezavisimo ot ih massy i razmera obladayut odnim i tem zhe uskoreniem i, esli
isklyuchit' soprotivlenie vozduha i tomu podobnye effekty, pod dejstviem sil
tyagoteniya dvizhutsya odinakovo. |jnshtejn pervym yasno i opredelenno pokazal,
chto tyazhelaya materiya prezhde vsego porozhdaet kriviznu prostranstva i chto
traektorii vseh tel, dvizhushchihsya v gravitacionnom pole, iskrivleny tol'ko
potomu, chto iskrivleno samo prostranstvo. Boyus' odnako, chto vam bez
dostatochnoj matematicheskoj podgotovki trudno razobrat'sya vo vsem etom.
- Nelegko, - soglasilsya mister Tompkins. - No skazhite mne, pozhalujsta,
byla by u nas ta geometriya, kotoroj menya uchili v shkole, esli by materii
voobshche ne bylo, i peresekalis' by togda parallel'nye pryamye?
- Parallel'nye ne peresekalis' by, - podtverdil professor, - no ni odno
material'noe sushchestvo ne moglo by proverit' eto.
- Mozhet byt', nikakogo Evklida v dejstvitel'nosti ne bylo i poetomu on
ne mog sozdat' geometriyu absolyutno pustogo prostranstva?
No professor yavno ne zhelal vdavat'sya v metafizicheskuyu diskussiyu.
Mezhdu tem izobrazhenie zapisnoj knizhki udalilos' v pervonachal'nom
napravlenii i nachalo priblizhat'sya vo vtoroj raz. Teper' ono bylo iskazheno
eshche bol'she, chem prezhde, i uznat' v nem "prizrak" zapisnoj knizhki bylo pochti
nevozmozhno. Po mneniyu professora, stol' sil'noe iskazhenie ob座asnyalos' tem,
chto lucham sveta na etot raz prihodilos' obhodit' ves' mir.
- Esli vy eshche raz oglyanetes', - obratilsya professor k misteru
Tompkinsu, - to uvidite moyu zapisnuyu knizhku, kotoraya, nakonec, vozvrashchaetsya
ko mne, sovershiv krugosvetnoe puteshestvie.
Professor protyanul ruku, pojmal zapisnuyu knizhku i zasunul ee v karman.
- V etoj vselennoj, kak vy mozhete ubedit'sya sami, tak mnogo pyli i
kamnej, - skazal professor, - chto pochti nevozmozhno okinut' vzglyadom ves'
mir. |ti besformennye teni, kotorye vy vidite vokrug nas, skoree vsego nashi
izobrazheniya i izobrazheniya okruzhayushchih predmetov. Odnako oni tak sil'no
iskazheny pyl'yu i defektami krivizny prostranstva, chto ya ne berus' skazat',
chemu sootvetstvuet kazhdoe takoe izobrazhenie.
- A ne nablyudaetsya li takoj zhe effekt v bol'shoj Vselennoj, gde my s
vami zhili ran'she? - sprosil mister Tompkins.
- Konechno, nablyudaetsya, - posledoval otvet, - no ta Vselennaya nastol'ko
velika, chto svetu trebuyutsya milliardy let, chtoby obojti ee. Vy mogli by, ne
pol'zuyas' zerkalom, uvidet', kak parikmaher postrig vas szadi, no lish' cherez
milliardy let posle togo, kak pobyvaete u parikmahera. Krome togo, veroyatnee
vsego mezhzvezdnaya pyl' polnost'yu zatemnit izobrazhenie. Kstati skazat', odin
anglijskij astronom predpolozhil dazhe kak-to raz, skoree v shutku, chem
vser'ez, chto vidimye sejchas zvezdy na nebe - ne bolee chem izobrazheniya zvezd,
sushchestvovavshih v ochen' dalekuyu epohu.
Ustav ot usilij ponyat' vse eti ob座asneniya, mister Tompkins oglyanulsya i
k svoemu bol'shomu udivleniyu zametil, chto kartina neba znachitel'no
izmenilas'. Pyli stalo zametno men'she, i on snyal s lica masku, kotoruyu
smasteril iz nosovogo platka. Nebol'shie kameshki proletali znachitel'no rezhe i
stukalis' o poverhnost' skaly s gorazdo men'shej energiej. CHto zhe kasaetsya
neskol'kih bol'shih skal, napodobie toj, na kotoroj nashli priyut i on sam,
mister Tompkins, i staryj professor, to teper' bol'shie skaly ne mayachili
poblizosti, kak v samom nachale, a udalilis' na bol'shie rasstoyaniya drug ot
druga i stali edva razlichimymi.
- ZHizn' yavno idet na lad, - podumal mister Tompkins, - a to ya vse
opasalsya, kak by odin iz etih bluzhdayushchih kamnej ne vrezalsya v menya.
- Mozhete li vy ob座asnit' izmeneniya, proishodyashchie vokrug nas? - sprosil
on, povernuvshis' k professoru.
- Ochen' dazhe prosto, - s gotovnost'yu otvetil tot. - Nasha malen'kaya
vselennaya ochen' bystro rasshiryaetsya i s teh por, kak my zdes' okazalis', ee
razmery uvelichilis' s desyati do primerno sotni kilometrov. Kak tol'ko ya
zdes' ochutilsya, rasshirenie bylo mne zametno po pokrasneniyu dalekih ob容ktov.
- YA tozhe zametil, chto na bol'shom rasstoyanii vse stanovitsya rozovym, -
podtverdil mister Tompkins, - no pochemu eto svidetel'stvuet o rasshirenii
vselennoj?
 - Dolzhno byt', vy zamechali, - nachal professor, - chto gudok
priblizhayushchegosya poezda zvuchit vysoko, no znachitel'no ponizhaetsya, kogda poezd
pronositsya mimo vas? |to tak nazyvaemyj effekt Doplera: zavisimost' vysoty
zvuka ot skorosti istochnika. Kogda rasshiryaetsya vse prostranstvo, kazhdyj
ob容kt, raspolozhennyj v nem, udalyaetsya so skorost'yu, proporcional'noj
rasstoyaniyu ot nablyudatelya do ob容kta. Svet, ispuskaemyj takimi ob容ktami,
krasneet, chto v akustike sootvetstvuet ponizheniyu vysoty tona. CHem dal'she
ob容kt, tem bystree on dvizhetsya i tem krasnee kazhetsya nam. V nashej dobroj
staroj Vselennoj, kotoraya takzhe rasshiryaetsya, eto pokrasnenie, ili, kak my
ego nazyvaem, krasnoe smeshchenie, pozvolyaet astronomam ocenivat' rasstoyaniya do
ochen' dalekih zvezdnyh oblakov. Naprimer, odno iz takih blizhajshih oblakov -
tak nazyvaemaya Tumannost' Andromedy - obnaruzhivaet 0,05 %-noe pokrasnenie,
chto sootvetstvuet rasstoyaniyu, prohodimomu svetom za vosem'sot tysyach let. No
sushchestvuyut takzhe tumannosti na predele razreshayushchej sposobnosti sovremennyh
teleskopov, kotorye obnaruzhivayut 15 %-noe pokrasnenie, chto sootvetstvuet
rasstoyaniyu v neskol'ko soten millionov svetovyh let. Predpolagaetsya, chto eti
tumannosti raspolozheny pochti na seredine ekvatora nashej bol'shoj Vselennoj i
ves' ob容m kosmicheskogo prostranstva, izvestnogo zemnym astronomam,
sostavlyaet znachitel'nuyu chast' polnogo ob容ma Vselennoj. Sovremennaya skorost'
ee rasshireniya sostavlyaet 0,00000001 % v god, kazhduyu sekundu radius Vselennoj
vozrastaet primerno na _desyat' millionov_ kilometrov. Nasha malaya vselennaya
rastet (po sravneniyu s bol'shoj) gorazdo bystree, i ee razmery uvelichivayutsya
primerno na 1 % v minutu.
- I takoe rasshirenie nikogda ne prekratitsya? - sprosil mister Tompkins.
- Razumeetsya, prekratitsya, - skazal professor, - a zatem nachnetsya
szhatie. Kazhdaya vselennaya pul'siruet mezhdu naimen'shim i naibol'shim radiusom.
Dlya bol'shoj Vselennoj period kolebanij ochen' velik i sostavlyaet chto-nibud'
okolo neskol'kih tysyach millionov let, no dlya nashej malen'koj vselennoj
period kolebanij sostavlyaet vsego lish' kakih-nibud' dva chasa. Dumayu, chto
sejchas my nablyudali sostoyanie ee naibol'shego rasshireniya. Vy zametili, kak
poholodalo?
Dejstvitel'no, teplovoe izluchenie, zapolnyayushchee vselennuyu i teper'
raspredelennoe po ochen' bol'shomu ob容mu, otdavalo malen'koj planete, na
kotoroj nahodilis' mister Tompkins i staryj professor, lish' nebol'shuyu toliku
tepla i temperatura byla blizka k tochke zamerzaniya.
- Horosho eshche, - skazal professor, - chto kogda my zdes' okazalis',
teplovogo izlucheniya bylo stol'ko, chto nemnogo tepla ono otdavalo dazhe na
stadii rasshireniya. V protivnom sluchae v nashej malen'koj vselennoj bylo by
nastol'ko holodno, chto vozduh vokrug nashej skaly skondensirovalsya by v
zhidkost' i my by nasmert' zamerzli. No szhatie uzhe nachalos' i skoro snova
budet teplo.
Vzglyanuv na nebo, mister Tompkins zametil, chto vse dalekie ob容kty
izmenili svoj cvet s rozovogo na fioletovyj. Po mneniyu professora, eto
oznachalo, chto vse nebesnye tela nachali priblizhat'sya k nim. Mister Tompkins
vspomnil privedennuyu professorom analogiyu s vysotoj zvuchaniya gudka
priblizhayushchegosya poezda i sodrognulsya ot straha.
- Esli vse teper' szhimaetsya, ne sleduet li ozhidat', chto vskore ogromnye
skaly, zapolnyayushchie vselennuyu, sblizyatsya i razdavyat nas? - s bespokojstvom
sprosil on professora.
- Vy sovershenno pravy, tak i proizojdet, - spokojno otvetil professor,
- no ya dumayu, chto eshche do togo, kak eto proizojdet, my oba raspademsya na
otdel'nye atomy iz-za neobychajno vysokoj temperatury. |to miniatyurnaya kopiya
kartiny konca bol'shoj Vselennoj, vse smeshaetsya v odnorodnyj shar raskalennogo
gaza i tol'ko posle togo, kak nastupit stadiya novogo rasshireniya, nachnetsya
novaya zhizn'.
- Nichego sebe perspektiva! - probormotal mister Tompkins. - V bol'shoj
Vselennoj u nas bylo do ee konca, kak vy upominali, milliardy let, a zdes'
vse proishodit slishkom bystro dlya menya! Mne zharko dazhe v pizhame!
- Pizhamu luchshe ne snimat', - posovetoval professor. - Vse ravno etim ne
pomozhesh'. Luchshe lech' i nablyudat' za proishodyashchim vokrug, poka vy smozhete.
Mister Tompkins nichego ne otvetil. ZHara stanovilas' nesterpimoj. Pyl',
sil'no uplotnivshayasya, stala sobirat'sya vokrug nego, i on pochuvstvoval sebya
kak by zavernutym v myagkoe teploe odeyalo. Mister Tompkins sdelal dvizhenie,
chtoby osvobodit'sya iz etogo kokona, i ruka ego neozhidanno okazalas' v
holodnom vozduhe.
- Dolzhno byt', vy zamechali, - nachal professor, - chto gudok
priblizhayushchegosya poezda zvuchit vysoko, no znachitel'no ponizhaetsya, kogda poezd
pronositsya mimo vas? |to tak nazyvaemyj effekt Doplera: zavisimost' vysoty
zvuka ot skorosti istochnika. Kogda rasshiryaetsya vse prostranstvo, kazhdyj
ob容kt, raspolozhennyj v nem, udalyaetsya so skorost'yu, proporcional'noj
rasstoyaniyu ot nablyudatelya do ob容kta. Svet, ispuskaemyj takimi ob容ktami,
krasneet, chto v akustike sootvetstvuet ponizheniyu vysoty tona. CHem dal'she
ob容kt, tem bystree on dvizhetsya i tem krasnee kazhetsya nam. V nashej dobroj
staroj Vselennoj, kotoraya takzhe rasshiryaetsya, eto pokrasnenie, ili, kak my
ego nazyvaem, krasnoe smeshchenie, pozvolyaet astronomam ocenivat' rasstoyaniya do
ochen' dalekih zvezdnyh oblakov. Naprimer, odno iz takih blizhajshih oblakov -
tak nazyvaemaya Tumannost' Andromedy - obnaruzhivaet 0,05 %-noe pokrasnenie,
chto sootvetstvuet rasstoyaniyu, prohodimomu svetom za vosem'sot tysyach let. No
sushchestvuyut takzhe tumannosti na predele razreshayushchej sposobnosti sovremennyh
teleskopov, kotorye obnaruzhivayut 15 %-noe pokrasnenie, chto sootvetstvuet
rasstoyaniyu v neskol'ko soten millionov svetovyh let. Predpolagaetsya, chto eti
tumannosti raspolozheny pochti na seredine ekvatora nashej bol'shoj Vselennoj i
ves' ob容m kosmicheskogo prostranstva, izvestnogo zemnym astronomam,
sostavlyaet znachitel'nuyu chast' polnogo ob容ma Vselennoj. Sovremennaya skorost'
ee rasshireniya sostavlyaet 0,00000001 % v god, kazhduyu sekundu radius Vselennoj
vozrastaet primerno na _desyat' millionov_ kilometrov. Nasha malaya vselennaya
rastet (po sravneniyu s bol'shoj) gorazdo bystree, i ee razmery uvelichivayutsya
primerno na 1 % v minutu.
- I takoe rasshirenie nikogda ne prekratitsya? - sprosil mister Tompkins.
- Razumeetsya, prekratitsya, - skazal professor, - a zatem nachnetsya
szhatie. Kazhdaya vselennaya pul'siruet mezhdu naimen'shim i naibol'shim radiusom.
Dlya bol'shoj Vselennoj period kolebanij ochen' velik i sostavlyaet chto-nibud'
okolo neskol'kih tysyach millionov let, no dlya nashej malen'koj vselennoj
period kolebanij sostavlyaet vsego lish' kakih-nibud' dva chasa. Dumayu, chto
sejchas my nablyudali sostoyanie ee naibol'shego rasshireniya. Vy zametili, kak
poholodalo?
Dejstvitel'no, teplovoe izluchenie, zapolnyayushchee vselennuyu i teper'
raspredelennoe po ochen' bol'shomu ob容mu, otdavalo malen'koj planete, na
kotoroj nahodilis' mister Tompkins i staryj professor, lish' nebol'shuyu toliku
tepla i temperatura byla blizka k tochke zamerzaniya.
- Horosho eshche, - skazal professor, - chto kogda my zdes' okazalis',
teplovogo izlucheniya bylo stol'ko, chto nemnogo tepla ono otdavalo dazhe na
stadii rasshireniya. V protivnom sluchae v nashej malen'koj vselennoj bylo by
nastol'ko holodno, chto vozduh vokrug nashej skaly skondensirovalsya by v
zhidkost' i my by nasmert' zamerzli. No szhatie uzhe nachalos' i skoro snova
budet teplo.
Vzglyanuv na nebo, mister Tompkins zametil, chto vse dalekie ob容kty
izmenili svoj cvet s rozovogo na fioletovyj. Po mneniyu professora, eto
oznachalo, chto vse nebesnye tela nachali priblizhat'sya k nim. Mister Tompkins
vspomnil privedennuyu professorom analogiyu s vysotoj zvuchaniya gudka
priblizhayushchegosya poezda i sodrognulsya ot straha.
- Esli vse teper' szhimaetsya, ne sleduet li ozhidat', chto vskore ogromnye
skaly, zapolnyayushchie vselennuyu, sblizyatsya i razdavyat nas? - s bespokojstvom
sprosil on professora.
- Vy sovershenno pravy, tak i proizojdet, - spokojno otvetil professor,
- no ya dumayu, chto eshche do togo, kak eto proizojdet, my oba raspademsya na
otdel'nye atomy iz-za neobychajno vysokoj temperatury. |to miniatyurnaya kopiya
kartiny konca bol'shoj Vselennoj, vse smeshaetsya v odnorodnyj shar raskalennogo
gaza i tol'ko posle togo, kak nastupit stadiya novogo rasshireniya, nachnetsya
novaya zhizn'.
- Nichego sebe perspektiva! - probormotal mister Tompkins. - V bol'shoj
Vselennoj u nas bylo do ee konca, kak vy upominali, milliardy let, a zdes'
vse proishodit slishkom bystro dlya menya! Mne zharko dazhe v pizhame!
- Pizhamu luchshe ne snimat', - posovetoval professor. - Vse ravno etim ne
pomozhesh'. Luchshe lech' i nablyudat' za proishodyashchim vokrug, poka vy smozhete.
Mister Tompkins nichego ne otvetil. ZHara stanovilas' nesterpimoj. Pyl',
sil'no uplotnivshayasya, stala sobirat'sya vokrug nego, i on pochuvstvoval sebya
kak by zavernutym v myagkoe teploe odeyalo. Mister Tompkins sdelal dvizhenie,
chtoby osvobodit'sya iz etogo kokona, i ruka ego neozhidanno okazalas' v
holodnom vozduhe.
 - Uzh ne prodelal li ya dyru v negostepriimnoj vselennoj? - bylo ego
pervoj mysl'yu. On hotel sprosit' ob etom professora, no togo nigde ne bylo.
Vmesto stavshej uzhe privychnoj skaly mister Tompkins razlichil v predrassvetnoj
mgle smutnye ochertaniya gostinichnogo nomera. On lezhal na krovati, plotno
zavernutyj v sherstyanoe odeyalo, vyprostav iz-pod odeyala odnu lish' ruku.
- Novaya zhizn' nachnetsya s rasshireniya! - podumal on, vspomniv slova
starogo professora. - Slava Bogu, my vse eshche rasshiryaemsya!
I mister Tompkins napravilsya v vannuyu, chtoby prinyat' utrennij dush.
Kosmicheskaya opera
Kogda utrom za zavtrakom mister Tompkins povedal professoru o svoem
sne, prisnivshemsya proshloj noch'yu, tot vyslushal ego ves'ma skepticheski.
- Kollaps nashej Vselennoj, - zametil on, - razumeetsya, byl by ves'ma
dramaticheskim koncom, odnako skorosti razbeganiya galaktik nastol'ko veliki,
chto perezhivaemaya nami stadiya rasshireniya nikogda ne perejdet v kollaps, nasha
Vselennaya budet neogranichenno rasshiryat'sya, a raspredelenie galaktik v
kosmicheskom prostranstve stanovit'sya vse bolee razrezhennym. Kogda vse
zvezdy, obrazuyushchie galaktiki, pogasnut iz-za ischerpaniya yadernogo topliva,
nasha Vselennaya prevratitsya v nabor holodnyh i temnyh skoplenij nebesnyh tel,
rasseyannyh v beskonechnyh prostorah.
Vprochem, nekotorye astronomy dumayut inache. Oni vydvigayut teoriyu tak
nazyvaemoj kosmologii stacionarnogo sostoyaniya, soglasno kotoroj Vselennaya
ostaetsya neizmennoj vo vremeni: ona sushchestvovala primerno v tom zhe
sostoyanii, v kakom my vidim ee segodnya, v beskonechno dalekom proshlom i budet
sushchestvovat' v takom zhe sostoyanii v beskonechno dalekom budushchem. Razumeetsya,
takaya teoriya velikolepno soglasuetsya so starym dobrym principom Britanskoj
imperii - sohranyat' v mire status kvo, odnako ya sklonen dumat', chto teoriya
stacionarnogo sostoyaniya neverna. Kstati skazat', odin iz sozdatelej etoj
novoj teorii - professor teoreticheskoj astronomii Kembridzhskogo universiteta
- napisal operu o stacionarnoj Vselennoj, prem'era kotoroj sostoitsya v
Kovent-Garden na sleduyushchej nedele. Pochemu by vam ne zakazat' bilety dlya Mod
i dlya sebya i ne poslushat' stol' neobychnuyu operu?
- Uzh ne prodelal li ya dyru v negostepriimnoj vselennoj? - bylo ego
pervoj mysl'yu. On hotel sprosit' ob etom professora, no togo nigde ne bylo.
Vmesto stavshej uzhe privychnoj skaly mister Tompkins razlichil v predrassvetnoj
mgle smutnye ochertaniya gostinichnogo nomera. On lezhal na krovati, plotno
zavernutyj v sherstyanoe odeyalo, vyprostav iz-pod odeyala odnu lish' ruku.
- Novaya zhizn' nachnetsya s rasshireniya! - podumal on, vspomniv slova
starogo professora. - Slava Bogu, my vse eshche rasshiryaemsya!
I mister Tompkins napravilsya v vannuyu, chtoby prinyat' utrennij dush.
Kosmicheskaya opera
Kogda utrom za zavtrakom mister Tompkins povedal professoru o svoem
sne, prisnivshemsya proshloj noch'yu, tot vyslushal ego ves'ma skepticheski.
- Kollaps nashej Vselennoj, - zametil on, - razumeetsya, byl by ves'ma
dramaticheskim koncom, odnako skorosti razbeganiya galaktik nastol'ko veliki,
chto perezhivaemaya nami stadiya rasshireniya nikogda ne perejdet v kollaps, nasha
Vselennaya budet neogranichenno rasshiryat'sya, a raspredelenie galaktik v
kosmicheskom prostranstve stanovit'sya vse bolee razrezhennym. Kogda vse
zvezdy, obrazuyushchie galaktiki, pogasnut iz-za ischerpaniya yadernogo topliva,
nasha Vselennaya prevratitsya v nabor holodnyh i temnyh skoplenij nebesnyh tel,
rasseyannyh v beskonechnyh prostorah.
Vprochem, nekotorye astronomy dumayut inache. Oni vydvigayut teoriyu tak
nazyvaemoj kosmologii stacionarnogo sostoyaniya, soglasno kotoroj Vselennaya
ostaetsya neizmennoj vo vremeni: ona sushchestvovala primerno v tom zhe
sostoyanii, v kakom my vidim ee segodnya, v beskonechno dalekom proshlom i budet
sushchestvovat' v takom zhe sostoyanii v beskonechno dalekom budushchem. Razumeetsya,
takaya teoriya velikolepno soglasuetsya so starym dobrym principom Britanskoj
imperii - sohranyat' v mire status kvo, odnako ya sklonen dumat', chto teoriya
stacionarnogo sostoyaniya neverna. Kstati skazat', odin iz sozdatelej etoj
novoj teorii - professor teoreticheskoj astronomii Kembridzhskogo universiteta
- napisal operu o stacionarnoj Vselennoj, prem'era kotoroj sostoitsya v
Kovent-Garden na sleduyushchej nedele. Pochemu by vam ne zakazat' bilety dlya Mod
i dlya sebya i ne poslushat' stol' neobychnuyu operu?
 CHerez neskol'ko dnej posle vozvrashcheniya v London s yuzhnogo poberezh'ya,
gde, kak eto chasto byvaet, stalo holodno i poshli dozhdi, mister Tompkins i
Mod sideli v udobnyh kreslah krasnogo barhata, ozhidaya, kogda vzov'etsya
zanaves i nachnetsya opera.
Prelyudiya byla ispolnena v tempe precipitevol issimevolmente, i dirizher
dvazhdy menyal svoj vorotnichok, prezhde chem prelyudiya podoshla k koncu. Nakonec,
kogda zanaves ryvkom podnyalsya, vse, kto nahodilsya v zale, vynuzhdeny byli
zakryt' glaza rukami - stol' oslepitel'no yarkim svetom byla zalita scena.
Potoki sveta, izlivavshiesya so sceny, vskore zapolnili ves' zritel'nyj zal ot
partera do balkona samogo verhnego yarusa, prevrativ ego v odin oslepitel'nyj
okean sveta. No vot svet stal postepenno merknut', i mister Tompkins
vnezapno obnaruzhil, chto kak by plavaet v temnom prostranstve, osveshchennom
mnozhestvom bystro vrashchayushchihsya kroshechnyh goryashchih fakelov, napominayushchih
ognennye kolesa, ispol'zuemye pri fejerverkah. Muzyka nevidimogo orkestra
smenilas' zvuchaniem organa, i mister Tompkins uvidel nepodaleku ot sebya
cheloveka v chernoj sutane i belom vorotnichke, kotoryj nosyat
svyashchennosluzhiteli. Vzglyanuv v libretto, mister Tompkins uznal, chto eto byl
abbat ZHorzh Lemetr iz Bel'gii, kotoryj pervym predlozhil teoriyu rasshiryayushchejsya
Vselennoj (etu teoriyu neredko nazyvayut teoriej "Bol'shogo Vzryva").
Pervye kuplety iz arii Lemetra mister Tompkins pomnit i ponyne:
O, Aiome prreemorrdialel
All-containeeng Atome!
Deessolved eento fragments exceedeengfy small
Galaxies forrmeeng,
Each wizprrimal energy!
Ot rradioactif Atome!
Ot all-containeeng Atome!
O, Univairrsale Aiome -
Worrk of Z'Lorrd!
Z long evolution
Tells of mightyfirreworrks
Zat ended een ashes and smouldairreeng weesps.
We stand on z'ceendairres
Fadeengsuns confironteengus,
Attempteeng to rremembairre
Z'splendeurofz brigine,
Q, Univairrsale Atome -
Worrkof Z'Lorrd {*}
CHerez neskol'ko dnej posle vozvrashcheniya v London s yuzhnogo poberezh'ya,
gde, kak eto chasto byvaet, stalo holodno i poshli dozhdi, mister Tompkins i
Mod sideli v udobnyh kreslah krasnogo barhata, ozhidaya, kogda vzov'etsya
zanaves i nachnetsya opera.
Prelyudiya byla ispolnena v tempe precipitevol issimevolmente, i dirizher
dvazhdy menyal svoj vorotnichok, prezhde chem prelyudiya podoshla k koncu. Nakonec,
kogda zanaves ryvkom podnyalsya, vse, kto nahodilsya v zale, vynuzhdeny byli
zakryt' glaza rukami - stol' oslepitel'no yarkim svetom byla zalita scena.
Potoki sveta, izlivavshiesya so sceny, vskore zapolnili ves' zritel'nyj zal ot
partera do balkona samogo verhnego yarusa, prevrativ ego v odin oslepitel'nyj
okean sveta. No vot svet stal postepenno merknut', i mister Tompkins
vnezapno obnaruzhil, chto kak by plavaet v temnom prostranstve, osveshchennom
mnozhestvom bystro vrashchayushchihsya kroshechnyh goryashchih fakelov, napominayushchih
ognennye kolesa, ispol'zuemye pri fejerverkah. Muzyka nevidimogo orkestra
smenilas' zvuchaniem organa, i mister Tompkins uvidel nepodaleku ot sebya
cheloveka v chernoj sutane i belom vorotnichke, kotoryj nosyat
svyashchennosluzhiteli. Vzglyanuv v libretto, mister Tompkins uznal, chto eto byl
abbat ZHorzh Lemetr iz Bel'gii, kotoryj pervym predlozhil teoriyu rasshiryayushchejsya
Vselennoj (etu teoriyu neredko nazyvayut teoriej "Bol'shogo Vzryva").
Pervye kuplety iz arii Lemetra mister Tompkins pomnit i ponyne:
O, Aiome prreemorrdialel
All-containeeng Atome!
Deessolved eento fragments exceedeengfy small
Galaxies forrmeeng,
Each wizprrimal energy!
Ot rradioactif Atome!
Ot all-containeeng Atome!
O, Univairrsale Aiome -
Worrk of Z'Lorrd!
Z long evolution
Tells of mightyfirreworrks
Zat ended een ashes and smouldairreeng weesps.
We stand on z'ceendairres
Fadeengsuns confironteengus,
Attempteeng to rremembairre
Z'splendeurofz brigine,
Q, Univairrsale Atome -
Worrkof Z'Lorrd {*}
 (O, Atom pervichnyj! {*}
Bessoderzhatel'nyj Atom!
Raspavshis' na mel'chajshie oskolki,
Ty obrazuesh' galaktiki,
Kazhduyu - so svoej pervichnoj energiej!
O, radioaktivnyj Atom!
Vsesoderzhitel'nyj Atom!
O, Atom Edinyj -
Tvorenie Gospoda!
Dolgaya evolyuciya
Govorit nam o chudovishchnyh fejerverkah,
Zakanchivavshihsya peplom i tleyushchimi uglyami.
My stoim na pepelishche,
I potuhshie solnca smotryat na nas,
Stoim, pytayas' vspomnit'
Velikolepie nachala mira.
O, Atom Edinyj -
Tvorenie Gospoda!)
{* Idya navstrechu pozhelaniyam melomanov, predpochitayushchih slushat' operu v
podlinnike, i cenitelej stilisticheskih krasot anglijskogo teksta, my
privodim vse opernye arii na yazyke originala, a dlya teh, kto interesuetsya
soderzhaniem, privodim perevod, ne iskazhennyj pogonej za rifmami. (Prim.
per.)}
Posle togo kak otec Lemetr zakonchil svoyu ariyu, otkuda ni voz'mis'
poyavilsya vysokij muzhchina, kotoryj (sudya po libretto) okazalsya russkim
fizikom Georgiem Gamovym, vot uzhe tri desyatiletiya provodyashchim svoj otpusk v
Soedinennyh SHtatah. Vot chto on zapel:
Good Abbe, ourrunderrstandink
It is same in many ways.
Univerrse has been expandink
Frrom the crradle of its days.
Univerrse has been expandink
Frrom the crradle of its days.
You have told it gains in motion,
Irregrret to disagrree,
And we differr in ourr notion
As to how it came to be.
And we differr in ourr notion
As to how it came to be.
It was neutrron fluid-neverr
Primal Atom, as you told.
It is infinite, as everr
It was infinite of old.
It is infinite, as everr
It was infinite of old.
On a limitless pavilion
In collapse, gas met its fate,
Yearrs ago (some thousand million)
Having come to densest state.
Yearrs ago {some thousand million)
Having come to densest state.
All the Space was then rresplendent
At that crrucialpoint in time.
Light to matterr was trranscendent
Much as meterr is, to rrhyme.
Light to matterr was trranscendent
Much as meterr is, to rrhyme.
For each ton ofrradiation
Then of matterr was an ounce,
Till the impulse t 'warrd inflation
In thatgrreatprrimeval bounce.
Till the impulse t 'warrd inflation
In that grreat prrimeval bounce.
Light by then was slowly palink,
Hundrred million yearrsgo by...
Matterr, over lightprrevailink,
Is in plentiful supply.
Matterr, overlightpirevailink,
Is in plentiful supply.
Matterr then began condensink
(Such are Jeans 'hypotheses).
Giant, gaseous clouds dispensink
Known asprrotogalaxies.
Giant, gaseous clouds dispensink
Known as prrotogalaxies.
Prrotogalaxies were shatterred,
Flying outward thrrough the night
Starrs werreforrmedfrom them, andscattemd
And the Space was filled with light.
Starrs werreforrmedfrrom them, andscattered
And the Space was filled with light
Galaxies arre everrspinnink,
Starrs will burrn to final sparrk.
Till ourr univerrse is thinnink
And is lifeless, cold and dank.
Till ourr univerrse is thinnink
And is lifeless, cold and darrk.
(O, Atom pervichnyj! {*}
Bessoderzhatel'nyj Atom!
Raspavshis' na mel'chajshie oskolki,
Ty obrazuesh' galaktiki,
Kazhduyu - so svoej pervichnoj energiej!
O, radioaktivnyj Atom!
Vsesoderzhitel'nyj Atom!
O, Atom Edinyj -
Tvorenie Gospoda!
Dolgaya evolyuciya
Govorit nam o chudovishchnyh fejerverkah,
Zakanchivavshihsya peplom i tleyushchimi uglyami.
My stoim na pepelishche,
I potuhshie solnca smotryat na nas,
Stoim, pytayas' vspomnit'
Velikolepie nachala mira.
O, Atom Edinyj -
Tvorenie Gospoda!)
{* Idya navstrechu pozhelaniyam melomanov, predpochitayushchih slushat' operu v
podlinnike, i cenitelej stilisticheskih krasot anglijskogo teksta, my
privodim vse opernye arii na yazyke originala, a dlya teh, kto interesuetsya
soderzhaniem, privodim perevod, ne iskazhennyj pogonej za rifmami. (Prim.
per.)}
Posle togo kak otec Lemetr zakonchil svoyu ariyu, otkuda ni voz'mis'
poyavilsya vysokij muzhchina, kotoryj (sudya po libretto) okazalsya russkim
fizikom Georgiem Gamovym, vot uzhe tri desyatiletiya provodyashchim svoj otpusk v
Soedinennyh SHtatah. Vot chto on zapel:
Good Abbe, ourrunderrstandink
It is same in many ways.
Univerrse has been expandink
Frrom the crradle of its days.
Univerrse has been expandink
Frrom the crradle of its days.
You have told it gains in motion,
Irregrret to disagrree,
And we differr in ourr notion
As to how it came to be.
And we differr in ourr notion
As to how it came to be.
It was neutrron fluid-neverr
Primal Atom, as you told.
It is infinite, as everr
It was infinite of old.
It is infinite, as everr
It was infinite of old.
On a limitless pavilion
In collapse, gas met its fate,
Yearrs ago (some thousand million)
Having come to densest state.
Yearrs ago {some thousand million)
Having come to densest state.
All the Space was then rresplendent
At that crrucialpoint in time.
Light to matterr was trranscendent
Much as meterr is, to rrhyme.
Light to matterr was trranscendent
Much as meterr is, to rrhyme.
For each ton ofrradiation
Then of matterr was an ounce,
Till the impulse t 'warrd inflation
In thatgrreatprrimeval bounce.
Till the impulse t 'warrd inflation
In that grreat prrimeval bounce.
Light by then was slowly palink,
Hundrred million yearrsgo by...
Matterr, over lightprrevailink,
Is in plentiful supply.
Matterr, overlightpirevailink,
Is in plentiful supply.
Matterr then began condensink
(Such are Jeans 'hypotheses).
Giant, gaseous clouds dispensink
Known asprrotogalaxies.
Giant, gaseous clouds dispensink
Known as prrotogalaxies.
Prrotogalaxies were shatterred,
Flying outward thrrough the night
Starrs werreforrmedfrom them, andscattemd
And the Space was filled with light.
Starrs werreforrmedfrrom them, andscattered
And the Space was filled with light
Galaxies arre everrspinnink,
Starrs will burrn to final sparrk.
Till ourr univerrse is thinnink
And is lifeless, cold and dank.
Till ourr univerrse is thinnink
And is lifeless, cold and darrk.
 (Slavnyj otche, nashi predstavleniya
Vo mnogom sovpadayut.
Vselennaya rasshiryaetsya
S samogo rozhdeniya.
Vselennaya rasshiryaetsya
S samogo rozhdeniya.
No vy utverzhdaete, chto ona vse pribavlyaet v dvizhenii.
K sozhaleniyu, ne mogu s vami soglasit'sya.
Rashodimsya my i v nashih predstavleniyah
Po povodu togo, kak eto mozhet proizojti.
Rashodimsya my i v nashih predstavleniyah
Po povodu togo, kak eto mozhet proizojti.
Snachala byla nejtronnaya zhidkost',
A ne pervichnyj Atom, kak vy utverzhdaete.
Ona prostiralas' beskonechno
I sushchestvovala beskonechno davno.
Ona prostiralas' beskonechno
I sushchestvovala beskonechno davno.
Pod beskonechnym shatrom
V kollapse gaz posledoval svoej sud'be,
I davnym-davno (neskol'ko tysyach millionov let nazad)
Pereshel v sostoyanie s naibol'shej plotnost'yu.
I davnym-davno (neskol'ko tysyach millionov let nazad)
Pereshel v sostoyanie s naibol'shej plotnost'yu.
Vse kosmicheskoe prostranstvo napolnilos' nesterpimym bleskom
V toj kriticheskoj tochke vo vremeni.
Svet preobladal nad materiej,
Kak metr nad rifmoj.
Svet preobladal nad materiej,
Kak metr nad rifmoj.
Na kazhduyu tonnu izlucheniya
Prihodilas' unciya materii,
Poka ne posledoval impul's k rasshireniyu -
Sil'nejshij pervichnyj tolchok.
Poka ne posledoval impul's k rasshireniyu -
Sil'nejshij pervichnyj tolchok.
Zatem svet stal medlenno merknut',
I dlilos' eto sotni millionov let...
Materiya stala preobladat' nad svetom
I ves'ma osnovatel'no.
Materiya stala preobladat' nad svetom
I ves'ma osnovatel'no.
Zatem materiya nachala kondensirovat'sya
(Takovy gipotezy Dzhinsa).
Obrazovalis' gigantskie gazovye oblaka,
Izvestnye kak protogalaktiki.
Obrazovalis' gigantskie gazovye oblaka,
Izvestnye kak protogalaktiki.
Protogalaktiki razbilis' vdrebezgi
I razletelis' v nochi.
Iz nih obrazovalis' zvezdy i rasseyalis',
I vse kosmicheskoe prostranstvo napolnilos' svetom.
Iz nih obrazovalis' zvezdy i rasseyalis',
I vse kosmicheskoe prostranstvo napolnilos' svetom.
Galaktiki budut bezostanovochno vrashchat'sya,
Zvezdy vygoryat do poslednej iskorki,
Vselennaya nasha budet stanovit'sya vse razrezhennej,
Poka ne prevratitsya v bezzhiznennuyu, holodnuyu i temnuyu pustynyu.
Vselennaya nasha budet stanovit'sya vse razrezhennej,
Poka ne prevratitsya v bezzhiznennuyu, holodnuyu i temnuyu pustynyu.)
Tret'yu ariyu, zapavshuyu v pamyat' misteru Tompkinsu, ispolnil avtor opery,
vnezapno materializovavshijsya iz nichego v prostranstve mezhdu yarko siyavshimi
galaktikami. On vynul iz karmana edva narodivshuyusya galaktiku i zapel:
(Slavnyj otche, nashi predstavleniya
Vo mnogom sovpadayut.
Vselennaya rasshiryaetsya
S samogo rozhdeniya.
Vselennaya rasshiryaetsya
S samogo rozhdeniya.
No vy utverzhdaete, chto ona vse pribavlyaet v dvizhenii.
K sozhaleniyu, ne mogu s vami soglasit'sya.
Rashodimsya my i v nashih predstavleniyah
Po povodu togo, kak eto mozhet proizojti.
Rashodimsya my i v nashih predstavleniyah
Po povodu togo, kak eto mozhet proizojti.
Snachala byla nejtronnaya zhidkost',
A ne pervichnyj Atom, kak vy utverzhdaete.
Ona prostiralas' beskonechno
I sushchestvovala beskonechno davno.
Ona prostiralas' beskonechno
I sushchestvovala beskonechno davno.
Pod beskonechnym shatrom
V kollapse gaz posledoval svoej sud'be,
I davnym-davno (neskol'ko tysyach millionov let nazad)
Pereshel v sostoyanie s naibol'shej plotnost'yu.
I davnym-davno (neskol'ko tysyach millionov let nazad)
Pereshel v sostoyanie s naibol'shej plotnost'yu.
Vse kosmicheskoe prostranstvo napolnilos' nesterpimym bleskom
V toj kriticheskoj tochke vo vremeni.
Svet preobladal nad materiej,
Kak metr nad rifmoj.
Svet preobladal nad materiej,
Kak metr nad rifmoj.
Na kazhduyu tonnu izlucheniya
Prihodilas' unciya materii,
Poka ne posledoval impul's k rasshireniyu -
Sil'nejshij pervichnyj tolchok.
Poka ne posledoval impul's k rasshireniyu -
Sil'nejshij pervichnyj tolchok.
Zatem svet stal medlenno merknut',
I dlilos' eto sotni millionov let...
Materiya stala preobladat' nad svetom
I ves'ma osnovatel'no.
Materiya stala preobladat' nad svetom
I ves'ma osnovatel'no.
Zatem materiya nachala kondensirovat'sya
(Takovy gipotezy Dzhinsa).
Obrazovalis' gigantskie gazovye oblaka,
Izvestnye kak protogalaktiki.
Obrazovalis' gigantskie gazovye oblaka,
Izvestnye kak protogalaktiki.
Protogalaktiki razbilis' vdrebezgi
I razletelis' v nochi.
Iz nih obrazovalis' zvezdy i rasseyalis',
I vse kosmicheskoe prostranstvo napolnilos' svetom.
Iz nih obrazovalis' zvezdy i rasseyalis',
I vse kosmicheskoe prostranstvo napolnilos' svetom.
Galaktiki budut bezostanovochno vrashchat'sya,
Zvezdy vygoryat do poslednej iskorki,
Vselennaya nasha budet stanovit'sya vse razrezhennej,
Poka ne prevratitsya v bezzhiznennuyu, holodnuyu i temnuyu pustynyu.
Vselennaya nasha budet stanovit'sya vse razrezhennej,
Poka ne prevratitsya v bezzhiznennuyu, holodnuyu i temnuyu pustynyu.)
Tret'yu ariyu, zapavshuyu v pamyat' misteru Tompkinsu, ispolnil avtor opery,
vnezapno materializovavshijsya iz nichego v prostranstve mezhdu yarko siyavshimi
galaktikami. On vynul iz karmana edva narodivshuyusya galaktiku i zapel:
 The universe, by Heaven's decree,
Was never formed in time gone by,
But is, has been, shail ever be -
For so say Bondi, Gold and I.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
The aging galaxies disperse,
Burn out, and exit from the scene.
But all the while, the universe
Is, was, shall ever be, has been.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
And still new galaxies condense
From nothing, as they did before.
(Lemaitre and Gamow, no offence!)
All was, will be for evermore.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
(Vselennaya ne voznikla vdrug,
Po veleniyu nebes, v proshlom.
Ona est', byla i budet vsegda,
Ibo tak govoryat Bondi, Goldiya.
Ostavajsya, o Kosmos, o Kosmos, navsegda odnim i tem zhe!
My provozglashaem stacionarnoe sostoyanie!
Stareyushchie galaktiki razbegayutsya,
Sgorayut i shodyat so sceny.
No vse ravno Vselennaya
Est', byla i budet vsegda.
Ostavajsya, o Kosmos, o Kosmos, navsegda odnim i tem zhe!
My provozglashaem stacionarnoe sostoyanie!
A mezhdu tem vse novye galaktiki kondensiruyutsya
Iz nichego, kak eto proishodilo v proshlom
(Lemetr i Gamov - eto ne vypad protiv vas!)
Vse bylo i budet navsegda.
Nesmotrya na stol' vdohnovlyayushchie slova, vse galaktiki v okruzhayushchem
prostranstve stali merknut'. Nakonec, barhatnyj zanaves opustilsya, i v
zritel'nom zale opernogo teatra zazhglis' kandelyabry.
- O, Siril, - uslyshal mister Tompkins golos Mod, - ya znayu, chto ty
sposoben usnut' gde ugodno i kogda ugodno, no zasypat' v Kovent-Garden tebe
vse-taki ne sledovalo! Ty prospal ves' spektakl'!
Kogda mister Tompkins provodil Mod do doma ee otca, staryj professor,
udobno raspolozhivshis' v kresle, prosmatrival tol'ko chto dostavlennyj vypusk
"Monthly Notices" (zhurnala "Ezhemesyachnye zametki").
- Nu i kak vam ponravilas' opera? - osvedomilsya professor.
- Velikolepno! - otozvalsya mister Tompkins. - Na menya osobenno sil'noe
vpechatlenie proizvela ariya o vechno sushchestvuyushchej Vselennoj. Ona zvuchit tak
uspokaivayushche!
- Poostorozhnej s etoj teoriej, - predostereg professor. - Razve vy ne
znaete poslovicu "Ne vse to zoloto, chto blestit"? YA kak raz chital stat'yu
kembridzhskogo astronoma Martina Rajla, kotoryj postroil gigantskij
radioteleskop, pozvolyayushchij obnaruzhivat' galaktiki na rasstoyaniyah, v
neskol'ko raz prevyshayushchih radius dejstviya dvuhsotdyujmovogo opticheskogo
teleskopa observatorii Maunt Palomar. Nablyudeniya Rajla pokazyvayut, chto ochen'
dalekie galaktiki raspolozheny gorazdo blizhe drug k drugu, chem sosednie
galaktiki.
- Vy hotite skazat', - poproboval utochnit' mister Tompkins, - chto
oblast' Vselennoj, v kotoroj my obitaem, naselena galaktikami ves'ma redko i
chto plotnost' naseleniya vozrastaet po mere togo, kak my udalyaemsya ot Zemli?
- Nichego podobnogo, - vozrazil professor. - Ne sleduet zabyvat' o tom,
chto iz-za konechnosti skorosti sveta, kogda vy smotrite daleko v glub'
kosmicheskogo prostranstva, vy kak by zaglyadyvaete daleko nazad vo vremeni.
Naprimer, tak kak svetu trebuetsya vosem' minut, chtoby dojti do nas ot
Solnca, vspyshku na Solnce zemnye astronomy nablyudayut s zapozdaniem v vosem'
minut. Fotografii nashego blizhajshego kosmicheskogo soseda - spiral'noj
galaktiki v sozvezdii Andromedy (kotoruyu vy, navernoe, videli v knigah po
astronomii; ona raspolozhena ot nas na rasstoyanii primerno v odin million
svetovyh let) - v dejstvitel'nosti pokazyvayut, kak eta galaktika vyglyadela
million let nazad. To, chto Rajl vidit ili, luchshe skazat', slyshit s pomoshch'yu
svoego radioteleskopa, sootvetstvuet situacii, sushchestvovavshej v toj dalekoj
chasti Vselennoj mnogie tysyachi millionov let nazad. Esli by nasha Vselennaya
nahodilas' v stacionarnom sostoyanii, to kartina ne dolzhna byla by izmenyat'sya
vo vremeni i ochen' dalekie galaktiki, nablyudaemye s Zemli, dolzhny byli by
byt' raspredeleny v kosmicheskom prostranstve ne plotnee i ne rezhe, chem
galaktiki v blizhajshej kosmicheskoj okrestnosti Zemli. Sledovatel'no, esli
nablyudeniya Rajla pokazyvayut, chto dalekie galaktiki raspolozheny v kosmicheskom
prostranstve plotnee, chem bolee blizkie galaktiki, to eto ekvivalentno
utverzhdeniyu o tom, chto v dalekom proshlom, tysyachi millionov let nazad,
galaktiki byli raspredeleny v prostranstve plotnee, chem teper'. YAsno, chto
takoe utverzhdenie protivorechit teorii stacionarnogo sostoyaniya Vselennoj i
podkreplyaet pervonachal'nuyu gipotezu, soglasno kotoroj galaktiki razbegayutsya
i plotnost' ih naseleniya ubyvaet. No, razumeetsya, my dolzhny soblyudat'
ostorozhnost' i podozhdat', poka rezul'taty Rajla ne budut podtverzhdeny.
- Kstati skazat', - prodolzhal professor, dostavaya iz karmana slozhennyj
listok bumagi, - odin iz moih uchenyh kolleg, obladayushchij poeticheskimi
naklonnostyami, nedavno napisal na etu temu stihotvorenie. Vot poslushajte:
"Your years of toil",
Said Ryle to Hoyle,
"Are wasted years, believe me.
The steady state
Is out of date.
Unless my eyes deceive me,
My telescope
Has dashed your hope;
Your tenets are refuted.
Let me be terse:
Our universe
Grows daily more diluted!"
Said Hoyle, "You quote
Lemaitre, I note,
And Gamow. Well, forget them!
That errant gang
And their Big Bang -
Why aid them and abet them?
You see, my friend,
It has no end
And there was no beginning,
As Bondi, Gold,
And I will hold
Until our hair is thinning."
"Not sol "cried Ryle
With rising bite
And straining at the tether;
"Far galaxies
Are, as one sees,
More tightly packed together!"
"You make me boil!"
Exploded Hoyle,
His statement rearranging;
"New matter's born
Each night and morn
The picture is unchanging!"
"Come off it, Hoyle!
I aim to foil
You yet" (The fun commences)
"And in a while",
Continued Ryle,
"I'll bring you to your sensed"
("Vse gody vashih hlopot, -
Skazal Rajl Hojlu, -
Naprasnaya trata vremeni, pover'te.
Stacionarnoe sostoyanie
Nyne ne v mode.
I esli moi glaza ne obmanyvayut menya,
Moj teleskop
Vdrebezgi razbil vashi nadezhdy;
Vasha teoriya oprovergnuta.
Pozvol'te mne skazat' pryamo:
Nasha Vselennaya
S kazhdym dnem stanovitsya vse bolee razrezhennoj!"
"Vy ssylaetes', - skazal Hojl, -
Kak ya poglyazhu, na Lemetra
I Gamova. Vybros'te ih iz golovy!
Ved' eto zabluzhdayushchayasya banda
I ih Bol'shoj Vzryv -
K chemu pomogat' im i pooshchryat' ih?
Vidite li, drug moj,
Vselennaya ne imeet konca
I nachala u nee takzhe ne bylo,
Na chem Bondi, Gold
I ya budem nastaivat',
Pokuda ne poredeyut nashi volosy!"
"Neverno! - vskrichal Rajl,
Razdrazhennyj i vne sebya ot yarosti, -
Ibo galaktiki,
Kak netrudno ubedit'sya,
Upakovany plotnee!"
"Vy prosto vyvodite menya iz terpeniya! -
Vzorvalsya Hojl,
Formuliruya svoe utverzhdenie po-inomu. -
Novaya materiya rozhdaetsya
Kazhduyu noch' i kazhdoe utro,
No kartina ostaetsya neizmennoj!"
"Da budet vam, Hojl!
Uzh teper' ya vser'ez voznamerilsya
Razrushit' vashi illyuzii (vot budet poteha!),
A poka, -
prodolzhal Rajl, -
YA privedu vas v chuvstvo!" {*})
{* Nedeli za dve do vyhoda v svet pervogo izdaniya etoj knigi poyavilas'
stat'ya Freda Hojla "Poslednie dostizheniya v kosmologii" (Nature, October 9,
1965, p. Ill), v kotoroj govorilos' sleduyushchee: "Hojl i ego sotrudniki
zanimalis' podschetom radioistochnikov... Rezul'taty podscheta radioistochnikov
ukazyvayut na to, chto Vselennaya v proshlom imela bol'shuyu plotnost', chem v
nastoyashchee vremya". Odnako avtor nastoyashchej knigi, porazmysliv, reshil ne
vnosit' kakie-libo izmeneniya v tekst arij "Kosmicheskoj opery", pamyatuya o
tom, chto opery, edinozhdy napisannye, stanovyatsya klassicheskimi: naprimer,
dazhe segodnya Dezdemona poet prekrasnuyu ariyu pered tem, kak umeret' ot ruk
Otello.}
- Mne ochen' hotelos' by uznat', - zametil mister Tompkins, - chem
zakonchitsya etot ne na shutku razgorevshijsya spor.
S etimi slovami on, pocelovav na proshchan'e miss Mod v shcheku, pozhelal ej i
staromu professoru spokojnoj nochi i otpravilsya k sebe domoj.
Glava 7
Kvantovyj bil'yard
Odnazhdy mister Tompkins vozvrashchalsya k sebe domoj strashno ustalyj posle
dolgogo rabochego dnya v banke, gde on sluzhil. Prohod mimo paba, mister
Tompkins reshil, chto bylo by nedurstvenno propustit' kruzhechku elya. Za pervoj
kruzhkoj posledovala drugaya, i vskore mister Tompkins pochuvstvoval, chto
golova u nego izryadno kruzhitsya. V zadnej komnate paba byla bil'yardnaya, gde
igroki v rubashkah s zasuchennymi rukavami tolpilis' vokrug central'nogo
stola. Mister Tompkins stal smutno pripominat', chto emu uzhe sluchalos' byvat'
zdes' i prezhde, kak vdrug kto-to iz ego priyatelej-klerkov potashchil mistera
Tompkinsa k stolu uchit'sya igrat' v bil'yard. Priblizivshis' k stolu, mister
Tompkins prinyalsya nablyudat' za igroj. CHto-to v nej pokazalos' emu ochen'
strannym! Igrayushchij stavil shar na stol i udaryal po sharu kiem. Sledya za
katyashchimsya sharom, mister Tompkins k svoemu bol'shomu udivleniyu zametil, chto
shar nachal "rasplyvat'sya". |to byla edinstvennoe vyrazhenie, kotoroe prishlo
emu na um pri vide strannogo povedeniya bil'yardnogo shara; kotoryj, katyas' po
zelenomu polyu, kazalsya vse bolee i bolee razmytym, na glazah utrachivaya
chetkost' svoih konturov. Kazalos', chto po zelenomu suknu katitsya ne odin
shar, a mnozhestvo sharov, k tomu zhe chastichno pronikayushchih drug v druga. Misteru
Tompkinsu chasto sluchalos' nablyudat' podobnye yavleniya i prezhde, no segodnya on
ne prinyal ni kapli viski i ne mog ponyat', pochemu tak proishodit.
- Posmotrim, - podumal mister Tompkins, - kak eta razmaznya iz shara
stolknetsya s drugoj takoj zhe razmaznej.
The universe, by Heaven's decree,
Was never formed in time gone by,
But is, has been, shail ever be -
For so say Bondi, Gold and I.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
The aging galaxies disperse,
Burn out, and exit from the scene.
But all the while, the universe
Is, was, shall ever be, has been.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
And still new galaxies condense
From nothing, as they did before.
(Lemaitre and Gamow, no offence!)
All was, will be for evermore.
Stay, O Cosmos, O Cosmos, stay the same!
We the Steady State proclaim!
(Vselennaya ne voznikla vdrug,
Po veleniyu nebes, v proshlom.
Ona est', byla i budet vsegda,
Ibo tak govoryat Bondi, Goldiya.
Ostavajsya, o Kosmos, o Kosmos, navsegda odnim i tem zhe!
My provozglashaem stacionarnoe sostoyanie!
Stareyushchie galaktiki razbegayutsya,
Sgorayut i shodyat so sceny.
No vse ravno Vselennaya
Est', byla i budet vsegda.
Ostavajsya, o Kosmos, o Kosmos, navsegda odnim i tem zhe!
My provozglashaem stacionarnoe sostoyanie!
A mezhdu tem vse novye galaktiki kondensiruyutsya
Iz nichego, kak eto proishodilo v proshlom
(Lemetr i Gamov - eto ne vypad protiv vas!)
Vse bylo i budet navsegda.
Nesmotrya na stol' vdohnovlyayushchie slova, vse galaktiki v okruzhayushchem
prostranstve stali merknut'. Nakonec, barhatnyj zanaves opustilsya, i v
zritel'nom zale opernogo teatra zazhglis' kandelyabry.
- O, Siril, - uslyshal mister Tompkins golos Mod, - ya znayu, chto ty
sposoben usnut' gde ugodno i kogda ugodno, no zasypat' v Kovent-Garden tebe
vse-taki ne sledovalo! Ty prospal ves' spektakl'!
Kogda mister Tompkins provodil Mod do doma ee otca, staryj professor,
udobno raspolozhivshis' v kresle, prosmatrival tol'ko chto dostavlennyj vypusk
"Monthly Notices" (zhurnala "Ezhemesyachnye zametki").
- Nu i kak vam ponravilas' opera? - osvedomilsya professor.
- Velikolepno! - otozvalsya mister Tompkins. - Na menya osobenno sil'noe
vpechatlenie proizvela ariya o vechno sushchestvuyushchej Vselennoj. Ona zvuchit tak
uspokaivayushche!
- Poostorozhnej s etoj teoriej, - predostereg professor. - Razve vy ne
znaete poslovicu "Ne vse to zoloto, chto blestit"? YA kak raz chital stat'yu
kembridzhskogo astronoma Martina Rajla, kotoryj postroil gigantskij
radioteleskop, pozvolyayushchij obnaruzhivat' galaktiki na rasstoyaniyah, v
neskol'ko raz prevyshayushchih radius dejstviya dvuhsotdyujmovogo opticheskogo
teleskopa observatorii Maunt Palomar. Nablyudeniya Rajla pokazyvayut, chto ochen'
dalekie galaktiki raspolozheny gorazdo blizhe drug k drugu, chem sosednie
galaktiki.
- Vy hotite skazat', - poproboval utochnit' mister Tompkins, - chto
oblast' Vselennoj, v kotoroj my obitaem, naselena galaktikami ves'ma redko i
chto plotnost' naseleniya vozrastaet po mere togo, kak my udalyaemsya ot Zemli?
- Nichego podobnogo, - vozrazil professor. - Ne sleduet zabyvat' o tom,
chto iz-za konechnosti skorosti sveta, kogda vy smotrite daleko v glub'
kosmicheskogo prostranstva, vy kak by zaglyadyvaete daleko nazad vo vremeni.
Naprimer, tak kak svetu trebuetsya vosem' minut, chtoby dojti do nas ot
Solnca, vspyshku na Solnce zemnye astronomy nablyudayut s zapozdaniem v vosem'
minut. Fotografii nashego blizhajshego kosmicheskogo soseda - spiral'noj
galaktiki v sozvezdii Andromedy (kotoruyu vy, navernoe, videli v knigah po
astronomii; ona raspolozhena ot nas na rasstoyanii primerno v odin million
svetovyh let) - v dejstvitel'nosti pokazyvayut, kak eta galaktika vyglyadela
million let nazad. To, chto Rajl vidit ili, luchshe skazat', slyshit s pomoshch'yu
svoego radioteleskopa, sootvetstvuet situacii, sushchestvovavshej v toj dalekoj
chasti Vselennoj mnogie tysyachi millionov let nazad. Esli by nasha Vselennaya
nahodilas' v stacionarnom sostoyanii, to kartina ne dolzhna byla by izmenyat'sya
vo vremeni i ochen' dalekie galaktiki, nablyudaemye s Zemli, dolzhny byli by
byt' raspredeleny v kosmicheskom prostranstve ne plotnee i ne rezhe, chem
galaktiki v blizhajshej kosmicheskoj okrestnosti Zemli. Sledovatel'no, esli
nablyudeniya Rajla pokazyvayut, chto dalekie galaktiki raspolozheny v kosmicheskom
prostranstve plotnee, chem bolee blizkie galaktiki, to eto ekvivalentno
utverzhdeniyu o tom, chto v dalekom proshlom, tysyachi millionov let nazad,
galaktiki byli raspredeleny v prostranstve plotnee, chem teper'. YAsno, chto
takoe utverzhdenie protivorechit teorii stacionarnogo sostoyaniya Vselennoj i
podkreplyaet pervonachal'nuyu gipotezu, soglasno kotoroj galaktiki razbegayutsya
i plotnost' ih naseleniya ubyvaet. No, razumeetsya, my dolzhny soblyudat'
ostorozhnost' i podozhdat', poka rezul'taty Rajla ne budut podtverzhdeny.
- Kstati skazat', - prodolzhal professor, dostavaya iz karmana slozhennyj
listok bumagi, - odin iz moih uchenyh kolleg, obladayushchij poeticheskimi
naklonnostyami, nedavno napisal na etu temu stihotvorenie. Vot poslushajte:
"Your years of toil",
Said Ryle to Hoyle,
"Are wasted years, believe me.
The steady state
Is out of date.
Unless my eyes deceive me,
My telescope
Has dashed your hope;
Your tenets are refuted.
Let me be terse:
Our universe
Grows daily more diluted!"
Said Hoyle, "You quote
Lemaitre, I note,
And Gamow. Well, forget them!
That errant gang
And their Big Bang -
Why aid them and abet them?
You see, my friend,
It has no end
And there was no beginning,
As Bondi, Gold,
And I will hold
Until our hair is thinning."
"Not sol "cried Ryle
With rising bite
And straining at the tether;
"Far galaxies
Are, as one sees,
More tightly packed together!"
"You make me boil!"
Exploded Hoyle,
His statement rearranging;
"New matter's born
Each night and morn
The picture is unchanging!"
"Come off it, Hoyle!
I aim to foil
You yet" (The fun commences)
"And in a while",
Continued Ryle,
"I'll bring you to your sensed"
("Vse gody vashih hlopot, -
Skazal Rajl Hojlu, -
Naprasnaya trata vremeni, pover'te.
Stacionarnoe sostoyanie
Nyne ne v mode.
I esli moi glaza ne obmanyvayut menya,
Moj teleskop
Vdrebezgi razbil vashi nadezhdy;
Vasha teoriya oprovergnuta.
Pozvol'te mne skazat' pryamo:
Nasha Vselennaya
S kazhdym dnem stanovitsya vse bolee razrezhennoj!"
"Vy ssylaetes', - skazal Hojl, -
Kak ya poglyazhu, na Lemetra
I Gamova. Vybros'te ih iz golovy!
Ved' eto zabluzhdayushchayasya banda
I ih Bol'shoj Vzryv -
K chemu pomogat' im i pooshchryat' ih?
Vidite li, drug moj,
Vselennaya ne imeet konca
I nachala u nee takzhe ne bylo,
Na chem Bondi, Gold
I ya budem nastaivat',
Pokuda ne poredeyut nashi volosy!"
"Neverno! - vskrichal Rajl,
Razdrazhennyj i vne sebya ot yarosti, -
Ibo galaktiki,
Kak netrudno ubedit'sya,
Upakovany plotnee!"
"Vy prosto vyvodite menya iz terpeniya! -
Vzorvalsya Hojl,
Formuliruya svoe utverzhdenie po-inomu. -
Novaya materiya rozhdaetsya
Kazhduyu noch' i kazhdoe utro,
No kartina ostaetsya neizmennoj!"
"Da budet vam, Hojl!
Uzh teper' ya vser'ez voznamerilsya
Razrushit' vashi illyuzii (vot budet poteha!),
A poka, -
prodolzhal Rajl, -
YA privedu vas v chuvstvo!" {*})
{* Nedeli za dve do vyhoda v svet pervogo izdaniya etoj knigi poyavilas'
stat'ya Freda Hojla "Poslednie dostizheniya v kosmologii" (Nature, October 9,
1965, p. Ill), v kotoroj govorilos' sleduyushchee: "Hojl i ego sotrudniki
zanimalis' podschetom radioistochnikov... Rezul'taty podscheta radioistochnikov
ukazyvayut na to, chto Vselennaya v proshlom imela bol'shuyu plotnost', chem v
nastoyashchee vremya". Odnako avtor nastoyashchej knigi, porazmysliv, reshil ne
vnosit' kakie-libo izmeneniya v tekst arij "Kosmicheskoj opery", pamyatuya o
tom, chto opery, edinozhdy napisannye, stanovyatsya klassicheskimi: naprimer,
dazhe segodnya Dezdemona poet prekrasnuyu ariyu pered tem, kak umeret' ot ruk
Otello.}
- Mne ochen' hotelos' by uznat', - zametil mister Tompkins, - chem
zakonchitsya etot ne na shutku razgorevshijsya spor.
S etimi slovami on, pocelovav na proshchan'e miss Mod v shcheku, pozhelal ej i
staromu professoru spokojnoj nochi i otpravilsya k sebe domoj.
Glava 7
Kvantovyj bil'yard
Odnazhdy mister Tompkins vozvrashchalsya k sebe domoj strashno ustalyj posle
dolgogo rabochego dnya v banke, gde on sluzhil. Prohod mimo paba, mister
Tompkins reshil, chto bylo by nedurstvenno propustit' kruzhechku elya. Za pervoj
kruzhkoj posledovala drugaya, i vskore mister Tompkins pochuvstvoval, chto
golova u nego izryadno kruzhitsya. V zadnej komnate paba byla bil'yardnaya, gde
igroki v rubashkah s zasuchennymi rukavami tolpilis' vokrug central'nogo
stola. Mister Tompkins stal smutno pripominat', chto emu uzhe sluchalos' byvat'
zdes' i prezhde, kak vdrug kto-to iz ego priyatelej-klerkov potashchil mistera
Tompkinsa k stolu uchit'sya igrat' v bil'yard. Priblizivshis' k stolu, mister
Tompkins prinyalsya nablyudat' za igroj. CHto-to v nej pokazalos' emu ochen'
strannym! Igrayushchij stavil shar na stol i udaryal po sharu kiem. Sledya za
katyashchimsya sharom, mister Tompkins k svoemu bol'shomu udivleniyu zametil, chto
shar nachal "rasplyvat'sya". |to byla edinstvennoe vyrazhenie, kotoroe prishlo
emu na um pri vide strannogo povedeniya bil'yardnogo shara; kotoryj, katyas' po
zelenomu polyu, kazalsya vse bolee i bolee razmytym, na glazah utrachivaya
chetkost' svoih konturov. Kazalos', chto po zelenomu suknu katitsya ne odin
shar, a mnozhestvo sharov, k tomu zhe chastichno pronikayushchih drug v druga. Misteru
Tompkinsu chasto sluchalos' nablyudat' podobnye yavleniya i prezhde, no segodnya on
ne prinyal ni kapli viski i ne mog ponyat', pochemu tak proishodit.
- Posmotrim, - podumal mister Tompkins, - kak eta razmaznya iz shara
stolknetsya s drugoj takoj zhe razmaznej.
 Dolzhno byt', igrok, nanesshij udar po sharu, byl znatokom svoego dela:
katyashchijsya shar stolknulsya s drugim sharom v lobovom udare, kak eto i
trebovalos'. Poslyshalsya gromkij stuk, i oba shara - pokoivshijsya i naletevshij
(mister Tompkins ne mog by s uverennost'yu skazat', gde kakoj shar) -
razletelis' "v raznye storony". Vyglyadelo eto, chto i govorit', ves'ma
stranno: na stole ne bylo bolee dvuh sharov, vyglyadevshih neskol'ko
razmazanno, a vmesto nih beschislennoe mnozhestvo sharov (vse - s _ves'ma_
smutnymi ochertaniyami i sil'no razmazannye) porazletalos' po napravleniyam,
sostavlyavshim ot 0o do 180o s napravleniem pervonachal'nogo soudareniya.
Bil'yardnyj shar skoree napominal prichudlivuyu volnu, rasprostranyayushchuyusya iz
tochki soudareniya sharov.
Prismotrevshis' povnimatel'nee, mister Tompkins zametil, chto
maksimal'nyj potok sharov napravlen v storonu pervonachal'nogo udara.
- Rasseyanie S-volny, - proiznes u nego za spinoj znakomyj golos, i
mister Tompkins, ne oborachivayas', uznal professora.
- Neuzheli i na etot raz chto-nibud' zdes' iskrivilos', - sprosil mister
Tompkins, - hotya poverhnost' bil'yardnogo stola mne kazhetsya gladkoj i rovnoj?
- Vy sovershenno pravy, - podtverdil professor, - prostranstvo v dannom
sluchae sovershenno ploskoe, a to, chto vy nablyudaete, v dejstvitel'nosti
predstavlyaet soboj kvantovoe yavlenie.
- Ah, eti matricy! - risknul sarkasticheski zametit' mister Tompkins.
- Tochnee, neopredelennost' dvizheniya, - zametil professor. - Vladelec
etoj bil'yardnoj sobral zdes' kollekciyu iz neskol'kih predmetov, stradayushchih,
esli mozhno tak vyrazit'sya, "kvantovym elefantizmom". V dejstvitel'nosti
kvantovym zakonam podchinyayutsya vse tela v prirode, no tak nazyvaemaya
kvantovaya postoyannaya, upravlyayushchaya vsemi etimi yavleniyami, chrezvychajno mala:
ee chislovoe znachenie imeet dvadcat' sem' nulej posle zapyatoj. CHto zhe
kasaetsya bil'yardnyh sharov, kotorye vy zdes' vidite, to ih kvantovaya
postoyannaya gorazdo bol'she (okolo edinicy), i poetomu vy mozhete nevooruzhennym
glazom videt' yavleniya, kotorye nauke udalos' otkryt' tol'ko s pomoshch'yu ves'ma
chuvstvitel'nyh i izoshchrennyh metodov nablyudeniya.
Tut professor umolk i nenadolgo zadumalsya.
- Ne hochu nichego kritikovat', - prodolzhal on, - no mne ochen' hotelos'
by znat', otkuda u vladel'ca bil'yardnoj eti shary. Strogo govorya, oni voobshche
ne mogut sushchestvovat', poskol'ku dlya vseh tel v mire kvantovaya postoyannaya
imeet odno i to zhe znachenie.
- Mozhet byt', ih importirovali iz kakogo-nibud' drugogo mira, -
vyskazal predpolozhenie mister Tompkins, no professor ne udovletvorilsya takoj
gipotezoj i ne izbavilsya ot ohvativshih ego podozrenij.
- Vy zametili, chto shary "rasplyvayutsya", - nachal on. - |to oznachaet, chto
ih polozhenie na bil'yardnom stole ne vpolne opredelenno. Vy ne mozhete tochno
ukazat', gde imenno nahoditsya shar. V luchshem sluchae vy mozhete utverzhdat'
lish', chto shar nahoditsya "v osnovnom zdes'" i "chastichno gde-to tam".
- Vse eto v vysshej stepeni neobychno, - probormotal mister Tompkins.
- Naoborot, - vozrazil professor, - eto absolyutno obychno v tom smysle,
chto vsegda proishodit s lyubym material'nym telom. Lish' iz-za chrezvychajno
malogo znacheniya kvantovoj postoyannoj i netochnosti obychnyh metodov nablyudeniya
lyudi ne zamechayut etoj neopredelennosti i delayut oshibochnyj vyvod o tom, chto
polozhenie i skorost' tela vsegda predstavlyayut soboj vpolne opredelennye
velichiny. V dejstvitel'nosti zhe i polozhenie, i skorost' vsegda v kakoj-to
stepeni neopredelenny, i chem tochnee izvestna odna iz velichin, tem bolee
razmazana drugaya. Kvantovaya postoyannaya kak raz i upravlyaet sootnosheniem
mezhdu etimi dvumya neopredelennostyami. Vot vzglyanite, ya nakladyvayu
opredelennye ogranicheniya na polozhenie etogo bil'yardnogo shara, zaklyuchaya ego
vnutr' derevyannogo treugol'nika.
Kak tol'ko shar okazalsya za derevyannym zaborchikom, vsya vnutrennost'
treugol'nika zapolnilas' bleskom slonovoj kosti.
- Vidite! - obradovalsya professor. - YA ogranichil polozhenie shara
razmerami prostranstva, zaklyuchennogo vnutri treugol'nika, t. e. kakimi-to
neskol'kimi dyujmami. I v rezul'tate - znachitel'naya neopredelennost' v
skorosti, shar tak begaet vnutri perimetra treugol'nika!
- A razve vy ne mogli by ostanovit' shar? - udivlenno sprosil mister
Tompkins.
- Ni v koem sluchae! |to fizicheski nevozmozhno, - posledoval otvet. -
Lyuboe telo, pomeshchennoe v zamknutoe prostranstvo, obladaet nekotorym
dvizheniem. My, fiziki, nazyvaem takoe dvizhenie nulevym. Takovo, naprimer,
dvizhenie elektronov v lyubom atome.
Poka mister Tompkins nablyudal za bil'yardnym sharom, mechushchimsya v
treugol'noj zagorodke, kak tigr v kletke, proizoshlo nechto ves'ma neobychnoe:
shar "prosochilsya" skvoz' stenku derevyannogo treugol'nika i v sleduyushchij moment
pokatilsya v dal'nij ugol bil'yardnogo stola. Samoe strannoe bylo v tom, chto
shar ne pereprygnul skvoz' derevyannuyu stenku, a proshel skvoz' nee, ne
podnimayas' nad urovnem bil'yardnogo stola.
Dolzhno byt', igrok, nanesshij udar po sharu, byl znatokom svoego dela:
katyashchijsya shar stolknulsya s drugim sharom v lobovom udare, kak eto i
trebovalos'. Poslyshalsya gromkij stuk, i oba shara - pokoivshijsya i naletevshij
(mister Tompkins ne mog by s uverennost'yu skazat', gde kakoj shar) -
razletelis' "v raznye storony". Vyglyadelo eto, chto i govorit', ves'ma
stranno: na stole ne bylo bolee dvuh sharov, vyglyadevshih neskol'ko
razmazanno, a vmesto nih beschislennoe mnozhestvo sharov (vse - s _ves'ma_
smutnymi ochertaniyami i sil'no razmazannye) porazletalos' po napravleniyam,
sostavlyavshim ot 0o do 180o s napravleniem pervonachal'nogo soudareniya.
Bil'yardnyj shar skoree napominal prichudlivuyu volnu, rasprostranyayushchuyusya iz
tochki soudareniya sharov.
Prismotrevshis' povnimatel'nee, mister Tompkins zametil, chto
maksimal'nyj potok sharov napravlen v storonu pervonachal'nogo udara.
- Rasseyanie S-volny, - proiznes u nego za spinoj znakomyj golos, i
mister Tompkins, ne oborachivayas', uznal professora.
- Neuzheli i na etot raz chto-nibud' zdes' iskrivilos', - sprosil mister
Tompkins, - hotya poverhnost' bil'yardnogo stola mne kazhetsya gladkoj i rovnoj?
- Vy sovershenno pravy, - podtverdil professor, - prostranstvo v dannom
sluchae sovershenno ploskoe, a to, chto vy nablyudaete, v dejstvitel'nosti
predstavlyaet soboj kvantovoe yavlenie.
- Ah, eti matricy! - risknul sarkasticheski zametit' mister Tompkins.
- Tochnee, neopredelennost' dvizheniya, - zametil professor. - Vladelec
etoj bil'yardnoj sobral zdes' kollekciyu iz neskol'kih predmetov, stradayushchih,
esli mozhno tak vyrazit'sya, "kvantovym elefantizmom". V dejstvitel'nosti
kvantovym zakonam podchinyayutsya vse tela v prirode, no tak nazyvaemaya
kvantovaya postoyannaya, upravlyayushchaya vsemi etimi yavleniyami, chrezvychajno mala:
ee chislovoe znachenie imeet dvadcat' sem' nulej posle zapyatoj. CHto zhe
kasaetsya bil'yardnyh sharov, kotorye vy zdes' vidite, to ih kvantovaya
postoyannaya gorazdo bol'she (okolo edinicy), i poetomu vy mozhete nevooruzhennym
glazom videt' yavleniya, kotorye nauke udalos' otkryt' tol'ko s pomoshch'yu ves'ma
chuvstvitel'nyh i izoshchrennyh metodov nablyudeniya.
Tut professor umolk i nenadolgo zadumalsya.
- Ne hochu nichego kritikovat', - prodolzhal on, - no mne ochen' hotelos'
by znat', otkuda u vladel'ca bil'yardnoj eti shary. Strogo govorya, oni voobshche
ne mogut sushchestvovat', poskol'ku dlya vseh tel v mire kvantovaya postoyannaya
imeet odno i to zhe znachenie.
- Mozhet byt', ih importirovali iz kakogo-nibud' drugogo mira, -
vyskazal predpolozhenie mister Tompkins, no professor ne udovletvorilsya takoj
gipotezoj i ne izbavilsya ot ohvativshih ego podozrenij.
- Vy zametili, chto shary "rasplyvayutsya", - nachal on. - |to oznachaet, chto
ih polozhenie na bil'yardnom stole ne vpolne opredelenno. Vy ne mozhete tochno
ukazat', gde imenno nahoditsya shar. V luchshem sluchae vy mozhete utverzhdat'
lish', chto shar nahoditsya "v osnovnom zdes'" i "chastichno gde-to tam".
- Vse eto v vysshej stepeni neobychno, - probormotal mister Tompkins.
- Naoborot, - vozrazil professor, - eto absolyutno obychno v tom smysle,
chto vsegda proishodit s lyubym material'nym telom. Lish' iz-za chrezvychajno
malogo znacheniya kvantovoj postoyannoj i netochnosti obychnyh metodov nablyudeniya
lyudi ne zamechayut etoj neopredelennosti i delayut oshibochnyj vyvod o tom, chto
polozhenie i skorost' tela vsegda predstavlyayut soboj vpolne opredelennye
velichiny. V dejstvitel'nosti zhe i polozhenie, i skorost' vsegda v kakoj-to
stepeni neopredelenny, i chem tochnee izvestna odna iz velichin, tem bolee
razmazana drugaya. Kvantovaya postoyannaya kak raz i upravlyaet sootnosheniem
mezhdu etimi dvumya neopredelennostyami. Vot vzglyanite, ya nakladyvayu
opredelennye ogranicheniya na polozhenie etogo bil'yardnogo shara, zaklyuchaya ego
vnutr' derevyannogo treugol'nika.
Kak tol'ko shar okazalsya za derevyannym zaborchikom, vsya vnutrennost'
treugol'nika zapolnilas' bleskom slonovoj kosti.
- Vidite! - obradovalsya professor. - YA ogranichil polozhenie shara
razmerami prostranstva, zaklyuchennogo vnutri treugol'nika, t. e. kakimi-to
neskol'kimi dyujmami. I v rezul'tate - znachitel'naya neopredelennost' v
skorosti, shar tak begaet vnutri perimetra treugol'nika!
- A razve vy ne mogli by ostanovit' shar? - udivlenno sprosil mister
Tompkins.
- Ni v koem sluchae! |to fizicheski nevozmozhno, - posledoval otvet. -
Lyuboe telo, pomeshchennoe v zamknutoe prostranstvo, obladaet nekotorym
dvizheniem. My, fiziki, nazyvaem takoe dvizhenie nulevym. Takovo, naprimer,
dvizhenie elektronov v lyubom atome.
Poka mister Tompkins nablyudal za bil'yardnym sharom, mechushchimsya v
treugol'noj zagorodke, kak tigr v kletke, proizoshlo nechto ves'ma neobychnoe:
shar "prosochilsya" skvoz' stenku derevyannogo treugol'nika i v sleduyushchij moment
pokatilsya v dal'nij ugol bil'yardnogo stola. Samoe strannoe bylo v tom, chto
shar ne pereprygnul skvoz' derevyannuyu stenku, a proshel skvoz' nee, ne
podnimayas' nad urovnem bil'yardnogo stola.
 - Vot vam vashe "nulevoe dvizhenie", - s uprekom skazal mister Tompkins.
- Ne uspeli oglyanut'sya, a shar "sbezhal". |to kak, po pravilam?
- Razumeetsya, v polnom sootvetstvii s pravilami, - soglasilsya
professor. - V dejstvitel'nosti vy vidite pered soboj odno iz naibolee
interesnyh sledstvij kvantovoj teorii. Esli energii dostatochno dlya togo,
chtoby telo moglo projti skvoz' stenku, to uderzhat' ego za stenkoj
nevozmozhno: rano ili pozdno ob容kt "prosochitsya" skvoz' stenku i budet takov.
- V takom sluchae ya ni za chto na svete ne pojdu v zoopark, - reshil pro
sebya mister Tompkins, i ego zhivoe voobrazhenie totchas zhe narisovalo uzhasayushchuyu
kartinu l'vov i tigrov, "prosachivayushchihsya" skvoz' stenki svoih kletok. Zatem
mysli mistera Tompkinsa prinyali neskol'ko inoe napravlenie: emu prividelsya
avtomobil', "prosochivshijsya" iz garazha skvoz' steny, kak dobroe staroe
prividenie vo vremena Srednevekov'ya.
- A skol'ko mne ponadobitsya zhdat', - pointeresovalsya mister Tompkins u
professora, - poka avtomashina, sdelannaya ne iz togo, iz chego delayut
avtomashiny zdes', a iz obychnoj stali, "prosochitsya" skvoz' stenu garazha,
postroennogo, skazhem, iz kirpichej? Hotel by ya svoimi glazami uvidet' takoe
"prosachivanie"!
Naskoro proizvedya v ume neobhodimye vychisleniya, professor privel otvet:
- ZHdat' vam pridetsya kakih-nibud' 1 000 000 000...000 000 let.
Dazhe privykshij k vnushitel'nym chislam v bankovskih schetah mister
Tompkins poteryal schet nulyam v chisle, privedennom professorom. Vprochem, on
neskol'ko uspokoilsya: chislo bylo dostatochno dlinnym dlya togo, chtoby mozhno
bylo ne bespokoit'sya o tom, kak by avtomashina ne sbezhala, "prosochivshis'"
skvoz' stenku v garazhe.
- Predpolozhim, chto vse, o chem vy mne rasskazali, ne vyzyvaet u menya ni
malejshih somnenij. Odnako mne vse zhe ostaetsya neponyatno, kak mozhno bylo by
nablyudat' takie veshchi (razumeetsya, ya ne govoryu ob etih bil'yardnyh sharah).
- Razumnoe vyrazhenie, - zametil professor. - Konechno, ya ne utverzhdayu,
budto kvantovye yavleniya mozhno bylo by nablyudat' na takih bol'shih telah, s
kakimi vam obychno prihoditsya imet' delo. Dejstvie kvantovyh zakonov
stanovitsya gorazdo bolee zametnym primenitel'no k ochen' malym massam -
takim, kak atomy ili elektrony. Dlya takih chastic kvantovye effekty nastol'ko
sil'ny, chto obychnaya mehanika stanovitsya sovershenno neprimenimoj.
Stolknovenie dvuh atomov vyglyadit tochno tak zhe, kak stolknovenie dvuh
bil'yardnyh sharov, kotoroe vy zdes' nablyudali, a dvizhenie elektronov v atome
ochen' napominaet "nulevoe dvizhenie" bil'yardnogo shara, kotoryj ya pomestil
vnutr' derevyannogo treugol'nika.
- A chasto li atomy vybegayut iz svoego garazha? - sprosil mister
Tompkins.
- O da, ves'ma chasto. Vam, konechno, prihodilos' slyshat' o radioaktivnyh
veshchestvah, atomy kotoryh preterpevayut spontannyj raspad, ispuskaya pri etom
ochen' bystrye chasticy. Takoj atom ili, tochnee, ego central'naya chast',
nazyvaemaya atomnym yadrom, ochen' napominaet garazh, v kotorom stoyat
avtomashiny, t. e. drugie chasticy. I chasticy ubegayut iz yadra, prosachivayas'
cherez stenki, - poroj vnutri yadra oni ne ostayutsya ni sekundy! V atomnyh
yadrah kvantovye yavleniya - delo sovershenno obychnoe!
Mister Tompkins poryadkom ustal ot stol' dlinnoj besedy i rasseyanno
oglyanulsya po storonam. Ego vnimanie privlekli bol'shie dedovskie chasy,
stoyavshie v uglu komnaty. Ih dlinnyj staromodnyj mayatnik sovershal medlennye
kolebaniya to v odnu, to v druguyu storonu.
- YA vizhu, vy zainteresovalis' chasami, - skazal professor. - Pered vami
ne sovsem obychnyj mehanizm, hotya nyne on neskol'ko ustarel. |ti chasy mogut
sluzhit' prekrasnoj illyustraciej togo, kak lyudi snachala myslili sebe
kvantovye yavleniya. Mayatnik chasov ustroen tak, chto amplituda ego kolebanij
mozhet vozrastat' tol'ko konechnymi shagami. Teper' vse chasovshchiki predpochitayut
pol'zovat'sya patentovannymi rasplyvayushchimisya mayatnikami.
- O, kak by ya hotel razobrat'sya v stol' slozhnyh voprosah! - voskliknul
mister Tompkins.
- Net nichego proshche, - otvetstvoval professor. - YA zashel v pab po puti
na svoyu lekciyu o kvantovoj teorii, potomu chto uvidel v okno vas. A teper'
mne pora otpravlyat'sya dal'she, chtoby ne opozdat' na lekciyu. Ne hotite li
pojti so mnoj?
- S prevelikim udovol'stviem! - soglasilsya mister Tompkins.
Bol'shaya auditoriya kak obychno byla do otkaza zapolnena studentami, i
mister Tompkins schital, chto emu ochen' povezlo, kogda on koe-kak primostilsya
na stupenyah prohoda.
- Ledi i dzhentl'meny, - nachal professor. - V dvuh moih predydushchih
lekciyah ya popytalsya pokazat' vam, kakim obrazom otkrytie sushchestvovaniya
verhnego predela vseh fizicheskih skorostej i analiz ponyatiya pryamoj privel
nas k polnomu peresmotru klassicheskih predstavlenij o prostranstve i
vremeni.
Odnako kriticheskij analiz osnov fiziki ne ostanovilsya na etoj stadii i
privel k eshche bolee porazitel'nym otkrytiyam i vyvodam. YA imeyu v vidu razdel
fiziki, poluchivshij nazvanie kvantovoj teorii. |tot razdel zanimaetsya
izucheniem ne stol'ko samih prostranstva i vremeni, skol'ko vzaimodejstviya i
dvizheniya material'nyh ob容ktov v prostranstve i vremeni. V klassicheskoj
fizike vsegda schitalos' samoochevidnym, chto vzaimodejstvie mezhdu lyubymi dvumya
material'nymi telami mozhet byt' sdelano nastol'ko malym, naskol'ko eto
trebuetsya po usloviyam eksperimenta, i dazhe, esli eto neobhodimo, prakticheski
svedeno k nulyu. Naprimer, esli pri issledovanii tepla, vydelyayushchegosya v
nekotoryh processah, voznikaet opasenie, chto vvodimyj termometr mozhet
zabrat' na sebya nekotoroe kolichestvo teploty i tem samym vnesti vozmushchenie v
normal'noe techenie processa, to eksperimentator prebyvaet v uverennosti,
chto, ispol'zuya termometr men'shih razmerov ili miniatyurnuyu termoparu, on
vsegda smozhet ponizit' vnosimoe vozmushchenie do urovnya, kotoryj ukladyvaetsya v
predely dopustimoj tochnosti izmerenij.
Ubezhdenie v tom, chto lyuboj fizicheskij process mozhet byt' v principe
nablyudaem s lyuboj trebuemoj tochnost'yu bez kakih-libo vozmushchenij, vnosimyh
nablyudeniem, bylo ves'ma sil'nym, i nikomu dazhe v golovu ne prihodilo
sformulirovat' stol' ochevidnoe dopushchenie v yavnom vide. Vse problemy,
svyazannye s vnosimymi pri nablyudenii vozmushcheniyami, schitalis' chisto
tehnicheskimi trudnostyami. Odnako novye eksperimental'nye fakty, nakoplennye
s nachala XX stoletiya, postoyanno vynuzhdali fizikov prihodit' k vyvodu, chto v
dejstvitel'nosti vse obstoit gorazdo slozhnee i _v prirode sushchestvuet
opredelennyj nizhnij predel vzaimodejstviya, kotoryj nikogda ne mozhet byt'
prevzojden_. |tot estestvennyj predel tochnosti prenebrezhimo mal dlya
vsevozmozhnyh processov, s kotorymi my stalkivaemsya v povsednevnoj zhizni, no
stanovitsya sushchestvennym pri rassmotrenii vzaimodejstvij, proishodyashchih v
takih mikroskopicheski-mehanicheskih sistemah, kak atomy i molekuly.
V 1900 g. nemeckij fizik Maks Plank, zanimayas' teoreticheskimi
issledovaniyami uslovij ravnovesiya mezhdu izlucheniem i veshchestvom, prishel k
udivitel'nomu vyvodu: _takoe ravnovesie nevozmozhno, esli vzaimodejstvie
mezhdu izlucheniem i veshchestvom proishodit ne nepreryvno, kak vsegda
predpolagalos', a v vide posledovatel'nosti otdel'nyh "soudarenij"_. Pri
kazhdom takom elementarnom akte vzaimodejstviya ot veshchestva izlucheniyu i ot
izlucheniya veshchestvu peredaetsya opredelennoe kolichestvo - "porciya" - energii.
Dlya dostizheniya trebuemogo ravnovesiya i soglasiya s eksperimental'nymi faktami
Planku ponadobilos' vvesti prostoe matematicheskoe sootnoshenie -
predpolozhit', chto mezhdu kolichestvom energii, peredavaemom pri kazhdom
elementarnom akte vzaimodejstviya, i chastotoj (velichinoj, obratnoj periodu)
processa, privodyashchego k peredache energii, sushchestvuet pryamaya
proporcional'nost'.
Inache govorya, esli koefficient proporcional'nosti oboznachit' cherez h,
to, soglasno prinyatoj Plankom gipoteze, minimal'naya porciya, ili kvant,
peredavaemoj energii opredelyaetsya vyrazheniem
E = hv, (1)
gde v - chastota. Postoyannaya L imeet chislovoe znachenie 6,547 h 10^27
erg.s i obychno nazyvaetsya postoyannoj Planka, ili kvantovoj postoyannoj. Maloe
chislovoe znachenie postoyannoj Planka ob座asnyaet, pochemu kvantovye yavleniya
obychno ne nablyudayutsya v povsednevnoj zhizni.
Dal'nejshee razvitie idej Planka svyazano s imenem |jnshtejna, kotoryj
cherez neskol'ko let prishel k vyvodu, chto _izluchenie ne tol'ko ispuskaetsya
opredelennymi diskretnymi porciyami, no i vsegda sushchestvuet v vide takih
diskretnyh "porcij energii", kotoruyu |jnshtejn nazval kvantami sveta_.
Poskol'ku kvanty sveta dvizhutsya, oni pomimo energii hv dolzhny obladat'
i opredelennym mehanicheskim impul'som, kotoryj, soglasno relyativistskoj
mehanike, dolzhen byt' raven ih energii, delennoj na skorost' sveta s.
Vspominaya, chto chastota sveta svyazana s ego dlinoj volny lyambda sootnosheniem
v = s/(lyambda), mehanicheskij impul's kvanta sveta mozhno zapisat' v vide
- Vot vam vashe "nulevoe dvizhenie", - s uprekom skazal mister Tompkins.
- Ne uspeli oglyanut'sya, a shar "sbezhal". |to kak, po pravilam?
- Razumeetsya, v polnom sootvetstvii s pravilami, - soglasilsya
professor. - V dejstvitel'nosti vy vidite pered soboj odno iz naibolee
interesnyh sledstvij kvantovoj teorii. Esli energii dostatochno dlya togo,
chtoby telo moglo projti skvoz' stenku, to uderzhat' ego za stenkoj
nevozmozhno: rano ili pozdno ob容kt "prosochitsya" skvoz' stenku i budet takov.
- V takom sluchae ya ni za chto na svete ne pojdu v zoopark, - reshil pro
sebya mister Tompkins, i ego zhivoe voobrazhenie totchas zhe narisovalo uzhasayushchuyu
kartinu l'vov i tigrov, "prosachivayushchihsya" skvoz' stenki svoih kletok. Zatem
mysli mistera Tompkinsa prinyali neskol'ko inoe napravlenie: emu prividelsya
avtomobil', "prosochivshijsya" iz garazha skvoz' steny, kak dobroe staroe
prividenie vo vremena Srednevekov'ya.
- A skol'ko mne ponadobitsya zhdat', - pointeresovalsya mister Tompkins u
professora, - poka avtomashina, sdelannaya ne iz togo, iz chego delayut
avtomashiny zdes', a iz obychnoj stali, "prosochitsya" skvoz' stenu garazha,
postroennogo, skazhem, iz kirpichej? Hotel by ya svoimi glazami uvidet' takoe
"prosachivanie"!
Naskoro proizvedya v ume neobhodimye vychisleniya, professor privel otvet:
- ZHdat' vam pridetsya kakih-nibud' 1 000 000 000...000 000 let.
Dazhe privykshij k vnushitel'nym chislam v bankovskih schetah mister
Tompkins poteryal schet nulyam v chisle, privedennom professorom. Vprochem, on
neskol'ko uspokoilsya: chislo bylo dostatochno dlinnym dlya togo, chtoby mozhno
bylo ne bespokoit'sya o tom, kak by avtomashina ne sbezhala, "prosochivshis'"
skvoz' stenku v garazhe.
- Predpolozhim, chto vse, o chem vy mne rasskazali, ne vyzyvaet u menya ni
malejshih somnenij. Odnako mne vse zhe ostaetsya neponyatno, kak mozhno bylo by
nablyudat' takie veshchi (razumeetsya, ya ne govoryu ob etih bil'yardnyh sharah).
- Razumnoe vyrazhenie, - zametil professor. - Konechno, ya ne utverzhdayu,
budto kvantovye yavleniya mozhno bylo by nablyudat' na takih bol'shih telah, s
kakimi vam obychno prihoditsya imet' delo. Dejstvie kvantovyh zakonov
stanovitsya gorazdo bolee zametnym primenitel'no k ochen' malym massam -
takim, kak atomy ili elektrony. Dlya takih chastic kvantovye effekty nastol'ko
sil'ny, chto obychnaya mehanika stanovitsya sovershenno neprimenimoj.
Stolknovenie dvuh atomov vyglyadit tochno tak zhe, kak stolknovenie dvuh
bil'yardnyh sharov, kotoroe vy zdes' nablyudali, a dvizhenie elektronov v atome
ochen' napominaet "nulevoe dvizhenie" bil'yardnogo shara, kotoryj ya pomestil
vnutr' derevyannogo treugol'nika.
- A chasto li atomy vybegayut iz svoego garazha? - sprosil mister
Tompkins.
- O da, ves'ma chasto. Vam, konechno, prihodilos' slyshat' o radioaktivnyh
veshchestvah, atomy kotoryh preterpevayut spontannyj raspad, ispuskaya pri etom
ochen' bystrye chasticy. Takoj atom ili, tochnee, ego central'naya chast',
nazyvaemaya atomnym yadrom, ochen' napominaet garazh, v kotorom stoyat
avtomashiny, t. e. drugie chasticy. I chasticy ubegayut iz yadra, prosachivayas'
cherez stenki, - poroj vnutri yadra oni ne ostayutsya ni sekundy! V atomnyh
yadrah kvantovye yavleniya - delo sovershenno obychnoe!
Mister Tompkins poryadkom ustal ot stol' dlinnoj besedy i rasseyanno
oglyanulsya po storonam. Ego vnimanie privlekli bol'shie dedovskie chasy,
stoyavshie v uglu komnaty. Ih dlinnyj staromodnyj mayatnik sovershal medlennye
kolebaniya to v odnu, to v druguyu storonu.
- YA vizhu, vy zainteresovalis' chasami, - skazal professor. - Pered vami
ne sovsem obychnyj mehanizm, hotya nyne on neskol'ko ustarel. |ti chasy mogut
sluzhit' prekrasnoj illyustraciej togo, kak lyudi snachala myslili sebe
kvantovye yavleniya. Mayatnik chasov ustroen tak, chto amplituda ego kolebanij
mozhet vozrastat' tol'ko konechnymi shagami. Teper' vse chasovshchiki predpochitayut
pol'zovat'sya patentovannymi rasplyvayushchimisya mayatnikami.
- O, kak by ya hotel razobrat'sya v stol' slozhnyh voprosah! - voskliknul
mister Tompkins.
- Net nichego proshche, - otvetstvoval professor. - YA zashel v pab po puti
na svoyu lekciyu o kvantovoj teorii, potomu chto uvidel v okno vas. A teper'
mne pora otpravlyat'sya dal'she, chtoby ne opozdat' na lekciyu. Ne hotite li
pojti so mnoj?
- S prevelikim udovol'stviem! - soglasilsya mister Tompkins.
Bol'shaya auditoriya kak obychno byla do otkaza zapolnena studentami, i
mister Tompkins schital, chto emu ochen' povezlo, kogda on koe-kak primostilsya
na stupenyah prohoda.
- Ledi i dzhentl'meny, - nachal professor. - V dvuh moih predydushchih
lekciyah ya popytalsya pokazat' vam, kakim obrazom otkrytie sushchestvovaniya
verhnego predela vseh fizicheskih skorostej i analiz ponyatiya pryamoj privel
nas k polnomu peresmotru klassicheskih predstavlenij o prostranstve i
vremeni.
Odnako kriticheskij analiz osnov fiziki ne ostanovilsya na etoj stadii i
privel k eshche bolee porazitel'nym otkrytiyam i vyvodam. YA imeyu v vidu razdel
fiziki, poluchivshij nazvanie kvantovoj teorii. |tot razdel zanimaetsya
izucheniem ne stol'ko samih prostranstva i vremeni, skol'ko vzaimodejstviya i
dvizheniya material'nyh ob容ktov v prostranstve i vremeni. V klassicheskoj
fizike vsegda schitalos' samoochevidnym, chto vzaimodejstvie mezhdu lyubymi dvumya
material'nymi telami mozhet byt' sdelano nastol'ko malym, naskol'ko eto
trebuetsya po usloviyam eksperimenta, i dazhe, esli eto neobhodimo, prakticheski
svedeno k nulyu. Naprimer, esli pri issledovanii tepla, vydelyayushchegosya v
nekotoryh processah, voznikaet opasenie, chto vvodimyj termometr mozhet
zabrat' na sebya nekotoroe kolichestvo teploty i tem samym vnesti vozmushchenie v
normal'noe techenie processa, to eksperimentator prebyvaet v uverennosti,
chto, ispol'zuya termometr men'shih razmerov ili miniatyurnuyu termoparu, on
vsegda smozhet ponizit' vnosimoe vozmushchenie do urovnya, kotoryj ukladyvaetsya v
predely dopustimoj tochnosti izmerenij.
Ubezhdenie v tom, chto lyuboj fizicheskij process mozhet byt' v principe
nablyudaem s lyuboj trebuemoj tochnost'yu bez kakih-libo vozmushchenij, vnosimyh
nablyudeniem, bylo ves'ma sil'nym, i nikomu dazhe v golovu ne prihodilo
sformulirovat' stol' ochevidnoe dopushchenie v yavnom vide. Vse problemy,
svyazannye s vnosimymi pri nablyudenii vozmushcheniyami, schitalis' chisto
tehnicheskimi trudnostyami. Odnako novye eksperimental'nye fakty, nakoplennye
s nachala XX stoletiya, postoyanno vynuzhdali fizikov prihodit' k vyvodu, chto v
dejstvitel'nosti vse obstoit gorazdo slozhnee i _v prirode sushchestvuet
opredelennyj nizhnij predel vzaimodejstviya, kotoryj nikogda ne mozhet byt'
prevzojden_. |tot estestvennyj predel tochnosti prenebrezhimo mal dlya
vsevozmozhnyh processov, s kotorymi my stalkivaemsya v povsednevnoj zhizni, no
stanovitsya sushchestvennym pri rassmotrenii vzaimodejstvij, proishodyashchih v
takih mikroskopicheski-mehanicheskih sistemah, kak atomy i molekuly.
V 1900 g. nemeckij fizik Maks Plank, zanimayas' teoreticheskimi
issledovaniyami uslovij ravnovesiya mezhdu izlucheniem i veshchestvom, prishel k
udivitel'nomu vyvodu: _takoe ravnovesie nevozmozhno, esli vzaimodejstvie
mezhdu izlucheniem i veshchestvom proishodit ne nepreryvno, kak vsegda
predpolagalos', a v vide posledovatel'nosti otdel'nyh "soudarenij"_. Pri
kazhdom takom elementarnom akte vzaimodejstviya ot veshchestva izlucheniyu i ot
izlucheniya veshchestvu peredaetsya opredelennoe kolichestvo - "porciya" - energii.
Dlya dostizheniya trebuemogo ravnovesiya i soglasiya s eksperimental'nymi faktami
Planku ponadobilos' vvesti prostoe matematicheskoe sootnoshenie -
predpolozhit', chto mezhdu kolichestvom energii, peredavaemom pri kazhdom
elementarnom akte vzaimodejstviya, i chastotoj (velichinoj, obratnoj periodu)
processa, privodyashchego k peredache energii, sushchestvuet pryamaya
proporcional'nost'.
Inache govorya, esli koefficient proporcional'nosti oboznachit' cherez h,
to, soglasno prinyatoj Plankom gipoteze, minimal'naya porciya, ili kvant,
peredavaemoj energii opredelyaetsya vyrazheniem
E = hv, (1)
gde v - chastota. Postoyannaya L imeet chislovoe znachenie 6,547 h 10^27
erg.s i obychno nazyvaetsya postoyannoj Planka, ili kvantovoj postoyannoj. Maloe
chislovoe znachenie postoyannoj Planka ob座asnyaet, pochemu kvantovye yavleniya
obychno ne nablyudayutsya v povsednevnoj zhizni.
Dal'nejshee razvitie idej Planka svyazano s imenem |jnshtejna, kotoryj
cherez neskol'ko let prishel k vyvodu, chto _izluchenie ne tol'ko ispuskaetsya
opredelennymi diskretnymi porciyami, no i vsegda sushchestvuet v vide takih
diskretnyh "porcij energii", kotoruyu |jnshtejn nazval kvantami sveta_.
Poskol'ku kvanty sveta dvizhutsya, oni pomimo energii hv dolzhny obladat'
i opredelennym mehanicheskim impul'som, kotoryj, soglasno relyativistskoj
mehanike, dolzhen byt' raven ih energii, delennoj na skorost' sveta s.
Vspominaya, chto chastota sveta svyazana s ego dlinoj volny lyambda sootnosheniem
v = s/(lyambda), mehanicheskij impul's kvanta sveta mozhno zapisat' v vide
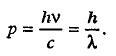 (2)
Poskol'ku mehanicheskoe dejstvie, proizvodimoe soudareniem dvizhushchegosya
ob容kta, opredelyaetsya ego impul'som, my zaklyuchaem, chto dejstvie kvantov
sveta vozrastaet pri ubyvanii dliny volny.
Odno iz luchshih eksperimental'nyh podtverzhdenij pravil'nosti
predstavleniya o kvantah sveta, a takzhe o pripisyvaemyh im energii i impul'se
bylo polucheno v rabote amerikanskogo fizika Artura Komptona. Issleduya
stolknovenie kvantov sveta i elektronov, Kompton pokazal, chto elektrony,
privedennye v dvizhenie pod dejstviem lucha sveta, vedut sebya tochno tak zhe,
kak esli by stolknulis' s chasticej, obladayushchej energiej i impul'som,
zadavaemymi formulami (1) i (2). Kak pokazali eksperimenty Komptona, sami
kvanty preterpevayut posle stolknoveniya s elektronami nekotorye izmeneniya
(izmenyaetsya ih chastota) v polnom soglasii s predskazaniem teorii.
V nastoyashchee vremya my vprave utverzhdat', chto v chasti, kasayushchejsya
vzaimodejstviya s veshchestvom, kvantovye svojstva izlucheniya nadlezhit schitat'
tverdo ustanovlennym eksperimental'nym faktom.
Dal'nejshee razvitie kvantovyh idej svyazano s imenem znamenitogo
datskogo fizika Nil'sa Bora, kotoryj v 1913 g. vpervye vyskazal ideyu o tom,
chto _vnutrennee dvizhenie lyuboj mehanicheskoj sistemy mozhet obladat' tol'ko
diskretnym naborom dopustimyh znachenij energii i dvizhenie mozhet izmenyat'
svoe sostoyanie tol'ko konechnymi shagami_, prichem pri kazhdom iz takih
perehodov izluchaetsya lish' opredelennoe kolichestvo energii. Matematicheskie
pravila, opredelyayushchie vozmozhnye sostoyaniya mehanicheskih sistem, bolee
slozhnye, chem v sluchae izlucheniya, i my ne budem privodit' ih zdes'. Upomyanem
lish' o tom, chto, kak i v sluchae kvantov sveta, impul's opredelyaetsya dlinoj
volny sveta, poetomu v mehanicheskoj sisteme impul's lyuboj dvizhushchejsya chasticy
svyazan s geometricheskimi razmerami toj oblasti prostranstva, v kotoroj ona
zaklyuchena, i sostavlyaet velichinu poryadka
(2)
Poskol'ku mehanicheskoe dejstvie, proizvodimoe soudareniem dvizhushchegosya
ob容kta, opredelyaetsya ego impul'som, my zaklyuchaem, chto dejstvie kvantov
sveta vozrastaet pri ubyvanii dliny volny.
Odno iz luchshih eksperimental'nyh podtverzhdenij pravil'nosti
predstavleniya o kvantah sveta, a takzhe o pripisyvaemyh im energii i impul'se
bylo polucheno v rabote amerikanskogo fizika Artura Komptona. Issleduya
stolknovenie kvantov sveta i elektronov, Kompton pokazal, chto elektrony,
privedennye v dvizhenie pod dejstviem lucha sveta, vedut sebya tochno tak zhe,
kak esli by stolknulis' s chasticej, obladayushchej energiej i impul'som,
zadavaemymi formulami (1) i (2). Kak pokazali eksperimenty Komptona, sami
kvanty preterpevayut posle stolknoveniya s elektronami nekotorye izmeneniya
(izmenyaetsya ih chastota) v polnom soglasii s predskazaniem teorii.
V nastoyashchee vremya my vprave utverzhdat', chto v chasti, kasayushchejsya
vzaimodejstviya s veshchestvom, kvantovye svojstva izlucheniya nadlezhit schitat'
tverdo ustanovlennym eksperimental'nym faktom.
Dal'nejshee razvitie kvantovyh idej svyazano s imenem znamenitogo
datskogo fizika Nil'sa Bora, kotoryj v 1913 g. vpervye vyskazal ideyu o tom,
chto _vnutrennee dvizhenie lyuboj mehanicheskoj sistemy mozhet obladat' tol'ko
diskretnym naborom dopustimyh znachenij energii i dvizhenie mozhet izmenyat'
svoe sostoyanie tol'ko konechnymi shagami_, prichem pri kazhdom iz takih
perehodov izluchaetsya lish' opredelennoe kolichestvo energii. Matematicheskie
pravila, opredelyayushchie vozmozhnye sostoyaniya mehanicheskih sistem, bolee
slozhnye, chem v sluchae izlucheniya, i my ne budem privodit' ih zdes'. Upomyanem
lish' o tom, chto, kak i v sluchae kvantov sveta, impul's opredelyaetsya dlinoj
volny sveta, poetomu v mehanicheskoj sisteme impul's lyuboj dvizhushchejsya chasticy
svyazan s geometricheskimi razmerami toj oblasti prostranstva, v kotoroj ona
zaklyuchena, i sostavlyaet velichinu poryadka
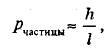 , (3)
gde l - linejnye razmery oblasti, v kotoroj proishodit dvizhenie. Iz-za
chrezvychajno malogo znacheniya kvantovoj postoyannoj kvantovye yavleniya
stanovyatsya sushchestvennymi tol'ko dlya dvizhenij, proishodyashchih v ochen' malyh
oblastyah prostranstva, naprimer vnutri atomov i molekul, i igrayut vazhnuyu
rol' v nashih znaniyah o vnutrennem stroenii veshchestva.
Odno iz naibolee pryamyh dokazatel'stv sushchestvovaniya posledovatel'nosti
diskretnyh sostoyanij etih krohotnyh mehanicheskih sistem bylo polucheno v
eksperimentah Dzhejmsa Franka i Gustava Gerca. Bombardiruya atomy elektronami
razlichnoj energii, eti fiziki zametili, chto opredelennye izmeneniya v
sostoyanii atoma proishodyat, tol'ko kogda energiya naletayushchih elektronov
dostigala opredelennyh diskretnyh znachenij. Esli energiya elektronov byla
nizhe opredelennogo predela, to soudareniya voobshche nikak ne skazyvalis' na
sostoyanii atoma, tak kak energiya, perenosimaya kazhdym elektronom, byla
nedostatochna dlya togo, chtoby podnyat' atom s pervogo kvantovogo sostoyaniya vo
vtoroe.
Rezyumiruya, mozhno skazat', chto k koncu opisannoj mnoj pervoj,
predvaritel'noj stadii razvitiya kvantovoj teorii byla dostignuta ne
modifikaciya fundamental'nyh ponyatij i principov klassicheskoj fiziki, a bolee
ili menee iskusstvennoe ogranichenie ves'ma zagadochnymi kvantovymi usloviyami,
vybirayushchimi iz nepreryvnogo mnozhestva klassicheski vozmozhnyh dvizhenij
diskretnoe podmnozhestvo "razreshennyh", ili "dopustimyh", dvizhenij. Odnako
esli my glubzhe vniknem v svyaz' mezhdu zakonami klassicheskoj mehaniki i
kvantovymi usloviyami, nalagaemymi nashim obobshchennym opytom, to obnaruzhim, chto
teoriya, poluchaemaya pri ob容dinenii klassicheskoj mehaniki s kvantovymi
usloviyami, stradaet logicheskoj neposledovatel'nost'yu i chto empiricheskie
kvantovye ogranicheniya delayut bessmyslennymi te fundamental'nye ponyatiya, na
kotoryh osnovana klassicheskaya mehanika. Dejstvitel'no, osnovnoe
predstavlenie klassicheskoj mehaniki otnositel'no dvizheniya zaklyuchaetsya v tom,
chto lyubaya dvizhushchayasya chastica zanimaet v lyuboj dannyj moment vremeni
opredelennoe polozhenie v prostranstve i obladaet opredelennoj skorost'yu,
harakterizuyushchej vremennye izmeneniya v polozhenii chasticy na traektorii.
Takie fundamental'nye ponyatiya, kak polozhenie, skorost' i traektoriya, na
kotorye opiraetsya vse velichestvennoe zdanie klassicheskoj mehaniki, postroeny
(kak i vse drugie nashi ponyatiya) na nablyudenii yavlenij v okruzhayushchem mire i,
podobno klassicheskim ponyatiyam prostranstva i vremeni, dolzhny byt'
sushchestvenno modificirovany, kogda nash opyt vtorgaetsya v novye, ne
issledovannye ranee, oblasti.
Esli ya sproshu kogo-nibud', pochemu on (ili ona) verit, chto lyubaya
dvizhushchayasya chastica zanimaet v lyuboj dannyj moment opredelennoe polozhenie,
opisyvaet vo vremya dvizheniya opredelennuyu liniyu, to v otvet moj sobesednik
skoree vsego skazhet: "Potomu, chto ya vizhu vse eto imenno tak, kogda nablyudayu
za dvizheniem". Proanaliziruem takoj metod obrazovaniya klassicheskogo ponyatiya
traektorii i popytaemsya vyyasnit', dejstvitel'no li on privodit k
opredelennomu rezul'tatu. Dlya etogo predstavim sebe myslenno fizika,
osnashchennogo vsevozmozhnoj chuvstvitel'nejshej apparaturoj i pytayushchegosya
prosledit' dvizhenie malen'kogo material'nogo tela, broshennogo so steny
laboratorii. Nash fizik reshaet proizvodit' nablyudeniya, glyadya, kak dvizhetsya
telo, i ispol'zuet dlya etogo nebol'shoj, no ochen' tochnyj teodolit.
Razumeetsya, chtoby uvidet' dvizhushcheesya telo, fiziku neobhodimo osveshchat' ego.
Znaya, chto svet okazyvaet davlenie na osveshchaemoe telo i poetomu vozmushchaet
dvizhenie tela, fizik reshaet osveshchat' telo korotkimi vspyshkami tol'ko v te
momenty, kogda on proizvodit nablyudeniya. V pervom eksperimente fizik
namerevaetsya nablyudat' tol'ko desyat' polozhenij tela na traektorii i vybiraet
istochnik, dayushchij vspyshki sveta, nastol'ko slabyj, chto integral'nyj effekt
svetovogo davleniya v techenie desyati posledovatel'nyh seansov nablyudeniya
lezhit v predelah trebuemoj tochnosti eksperimenta. Takim obrazom, osveshchaya
padayushchee telo desyat'yu vspyshkami, nash fizik poluchaet v predelah trebuemoj
tochnosti desyat' tochek na traektorii.
, (3)
gde l - linejnye razmery oblasti, v kotoroj proishodit dvizhenie. Iz-za
chrezvychajno malogo znacheniya kvantovoj postoyannoj kvantovye yavleniya
stanovyatsya sushchestvennymi tol'ko dlya dvizhenij, proishodyashchih v ochen' malyh
oblastyah prostranstva, naprimer vnutri atomov i molekul, i igrayut vazhnuyu
rol' v nashih znaniyah o vnutrennem stroenii veshchestva.
Odno iz naibolee pryamyh dokazatel'stv sushchestvovaniya posledovatel'nosti
diskretnyh sostoyanij etih krohotnyh mehanicheskih sistem bylo polucheno v
eksperimentah Dzhejmsa Franka i Gustava Gerca. Bombardiruya atomy elektronami
razlichnoj energii, eti fiziki zametili, chto opredelennye izmeneniya v
sostoyanii atoma proishodyat, tol'ko kogda energiya naletayushchih elektronov
dostigala opredelennyh diskretnyh znachenij. Esli energiya elektronov byla
nizhe opredelennogo predela, to soudareniya voobshche nikak ne skazyvalis' na
sostoyanii atoma, tak kak energiya, perenosimaya kazhdym elektronom, byla
nedostatochna dlya togo, chtoby podnyat' atom s pervogo kvantovogo sostoyaniya vo
vtoroe.
Rezyumiruya, mozhno skazat', chto k koncu opisannoj mnoj pervoj,
predvaritel'noj stadii razvitiya kvantovoj teorii byla dostignuta ne
modifikaciya fundamental'nyh ponyatij i principov klassicheskoj fiziki, a bolee
ili menee iskusstvennoe ogranichenie ves'ma zagadochnymi kvantovymi usloviyami,
vybirayushchimi iz nepreryvnogo mnozhestva klassicheski vozmozhnyh dvizhenij
diskretnoe podmnozhestvo "razreshennyh", ili "dopustimyh", dvizhenij. Odnako
esli my glubzhe vniknem v svyaz' mezhdu zakonami klassicheskoj mehaniki i
kvantovymi usloviyami, nalagaemymi nashim obobshchennym opytom, to obnaruzhim, chto
teoriya, poluchaemaya pri ob容dinenii klassicheskoj mehaniki s kvantovymi
usloviyami, stradaet logicheskoj neposledovatel'nost'yu i chto empiricheskie
kvantovye ogranicheniya delayut bessmyslennymi te fundamental'nye ponyatiya, na
kotoryh osnovana klassicheskaya mehanika. Dejstvitel'no, osnovnoe
predstavlenie klassicheskoj mehaniki otnositel'no dvizheniya zaklyuchaetsya v tom,
chto lyubaya dvizhushchayasya chastica zanimaet v lyuboj dannyj moment vremeni
opredelennoe polozhenie v prostranstve i obladaet opredelennoj skorost'yu,
harakterizuyushchej vremennye izmeneniya v polozhenii chasticy na traektorii.
Takie fundamental'nye ponyatiya, kak polozhenie, skorost' i traektoriya, na
kotorye opiraetsya vse velichestvennoe zdanie klassicheskoj mehaniki, postroeny
(kak i vse drugie nashi ponyatiya) na nablyudenii yavlenij v okruzhayushchem mire i,
podobno klassicheskim ponyatiyam prostranstva i vremeni, dolzhny byt'
sushchestvenno modificirovany, kogda nash opyt vtorgaetsya v novye, ne
issledovannye ranee, oblasti.
Esli ya sproshu kogo-nibud', pochemu on (ili ona) verit, chto lyubaya
dvizhushchayasya chastica zanimaet v lyuboj dannyj moment opredelennoe polozhenie,
opisyvaet vo vremya dvizheniya opredelennuyu liniyu, to v otvet moj sobesednik
skoree vsego skazhet: "Potomu, chto ya vizhu vse eto imenno tak, kogda nablyudayu
za dvizheniem". Proanaliziruem takoj metod obrazovaniya klassicheskogo ponyatiya
traektorii i popytaemsya vyyasnit', dejstvitel'no li on privodit k
opredelennomu rezul'tatu. Dlya etogo predstavim sebe myslenno fizika,
osnashchennogo vsevozmozhnoj chuvstvitel'nejshej apparaturoj i pytayushchegosya
prosledit' dvizhenie malen'kogo material'nogo tela, broshennogo so steny
laboratorii. Nash fizik reshaet proizvodit' nablyudeniya, glyadya, kak dvizhetsya
telo, i ispol'zuet dlya etogo nebol'shoj, no ochen' tochnyj teodolit.
Razumeetsya, chtoby uvidet' dvizhushcheesya telo, fiziku neobhodimo osveshchat' ego.
Znaya, chto svet okazyvaet davlenie na osveshchaemoe telo i poetomu vozmushchaet
dvizhenie tela, fizik reshaet osveshchat' telo korotkimi vspyshkami tol'ko v te
momenty, kogda on proizvodit nablyudeniya. V pervom eksperimente fizik
namerevaetsya nablyudat' tol'ko desyat' polozhenij tela na traektorii i vybiraet
istochnik, dayushchij vspyshki sveta, nastol'ko slabyj, chto integral'nyj effekt
svetovogo davleniya v techenie desyati posledovatel'nyh seansov nablyudeniya
lezhit v predelah trebuemoj tochnosti eksperimenta. Takim obrazom, osveshchaya
padayushchee telo desyat'yu vspyshkami, nash fizik poluchaet v predelah trebuemoj
tochnosti desyat' tochek na traektorii.
 Zatem on hochet povtorit' eksperiment i poluchit' sto tochek. Fizik znaet,
chto sto posledovatel'nyh vspyshek slishkom sil'no vozmutyat dvizhenie i,
gotovyas' ko vtoroj serii nablyudenij, vybiraet fonar', dayushchij v desyat' raz
menee intensivnoe osveshchenie. Dlya tret'ej serii nablyudenij, gotovyas' poluchit'
tysyachu tochek na traektorii, fizik vybiraet fonar', dayushchij v sto raz menee
intensivnoe osveshchenie, chem istochnik sveta, kotoryj byl ispol'zovan v pervoj
serii nablyudenij.
Prodolzhaya v tom zhe duhe i postoyanno umen'shaya intensivnost' osveshcheniya,
davaemogo istochnikom, fizik mozhet poluchit' na traektorii stol'ko tochek,
skol'ko sochtet nuzhnym, ne uvelichivaya eksperimental'nuyu oshibku vyshe
ustanovlennogo s samogo nachala predela. Opisannaya mnoj sil'no
idealizirovannaya, no principial'no vpolne osushchestvimaya procedura
predstavlyaet soboj strogo logicheskij sposob, pozvolyayushchij postroit' dvizhenie
po traektorii, "glyadya na dvizhushcheesya telo", i, kak vy vidite, v ramkah
klassicheskoj fiziki takoe postroenie vpolne vozmozhno.
Popytaemsya teper' vyyasnit', chto proizojdet, esli my vvedem kvantovye
ogranicheniya i uchtem, chto dejstvie lyubogo izlucheniya mozhet peredavat'sya tol'ko
v forme kvantov sveta. My videli, chto nablyudatel' postoyanno umen'shal
kolichestvo sveta, padayushchego na dvizhushcheesya telo, i teper' nam sleduet
ozhidat', chto, dojdya do odnogo kvanta, nash fizik ne smozhet prodolzhat' v tom
zhe duhe i dal'she. Ot dvizhushchegosya tela budet otrazhat'sya libo ves' kvant sveta
celikom, libo nichego, i v poslednem sluchae nablyudenie stanovitsya
nevozmozhnym. My znaem, chto v rezul'tate stolknoveniya s kvantom sveta dlina
volny sveta umen'shaetsya i nash nablyudatel', takzhe znaya ob etom, zavedomo
popytaetsya ispol'zovat' dlya svoih nablyudenij svet so vse uvelichivayushchejsya
dlinoj volny, chtoby kompensirovat' chislo nablyudenij. No tut ego podsteregaet
drugaya trudnost'.
Horosho izvestno, chto pri ispol'zovanii sveta opredelennoj dliny volny
nevozmozhno razlichit' detali, razmery kotoryh men'she dliny volny: nel'zya
narisovat' persidskuyu miniatyuru malyarnoj kist'yu! No ispol'zuya vse bolee
dlinnye volny, nash fizik isportit ocenku polozheniya kazhdoj tochki i vskore
dostignet toj stadii, kogda kazhdaya ocenka budet soderzhat' pogreshnost', ili
neopredelennost', velichina kotoroj sravnima s razmerami vsej ego laboratorii
i prevyshaet ih. Tem samym nash nablyudatel' budet vynuzhden v konce koncov
pojti na kompromiss mezhdu bol'shim chislom nablyudaemyh tochek i
neopredelennost'yu v ocenke polozheniya kazhdoj tochki i ne smozhet poluchit'
tochnuyu traektoriyu - v vide linii v matematicheskom smysle v otlichie ot svoih
klassicheskih kolleg. V luchshem sluchae kvantovyj nablyudatel' poluchit ves'ma
shirokuyu razmazannuyu polosu, i esli on popytaetsya postroit' ponyatie
traektorii, opirayas' na svoj opyt, to ono budet sil'no otlichat'sya ot
klassicheskogo ponyatiya traektorii.
Zatem on hochet povtorit' eksperiment i poluchit' sto tochek. Fizik znaet,
chto sto posledovatel'nyh vspyshek slishkom sil'no vozmutyat dvizhenie i,
gotovyas' ko vtoroj serii nablyudenij, vybiraet fonar', dayushchij v desyat' raz
menee intensivnoe osveshchenie. Dlya tret'ej serii nablyudenij, gotovyas' poluchit'
tysyachu tochek na traektorii, fizik vybiraet fonar', dayushchij v sto raz menee
intensivnoe osveshchenie, chem istochnik sveta, kotoryj byl ispol'zovan v pervoj
serii nablyudenij.
Prodolzhaya v tom zhe duhe i postoyanno umen'shaya intensivnost' osveshcheniya,
davaemogo istochnikom, fizik mozhet poluchit' na traektorii stol'ko tochek,
skol'ko sochtet nuzhnym, ne uvelichivaya eksperimental'nuyu oshibku vyshe
ustanovlennogo s samogo nachala predela. Opisannaya mnoj sil'no
idealizirovannaya, no principial'no vpolne osushchestvimaya procedura
predstavlyaet soboj strogo logicheskij sposob, pozvolyayushchij postroit' dvizhenie
po traektorii, "glyadya na dvizhushcheesya telo", i, kak vy vidite, v ramkah
klassicheskoj fiziki takoe postroenie vpolne vozmozhno.
Popytaemsya teper' vyyasnit', chto proizojdet, esli my vvedem kvantovye
ogranicheniya i uchtem, chto dejstvie lyubogo izlucheniya mozhet peredavat'sya tol'ko
v forme kvantov sveta. My videli, chto nablyudatel' postoyanno umen'shal
kolichestvo sveta, padayushchego na dvizhushcheesya telo, i teper' nam sleduet
ozhidat', chto, dojdya do odnogo kvanta, nash fizik ne smozhet prodolzhat' v tom
zhe duhe i dal'she. Ot dvizhushchegosya tela budet otrazhat'sya libo ves' kvant sveta
celikom, libo nichego, i v poslednem sluchae nablyudenie stanovitsya
nevozmozhnym. My znaem, chto v rezul'tate stolknoveniya s kvantom sveta dlina
volny sveta umen'shaetsya i nash nablyudatel', takzhe znaya ob etom, zavedomo
popytaetsya ispol'zovat' dlya svoih nablyudenij svet so vse uvelichivayushchejsya
dlinoj volny, chtoby kompensirovat' chislo nablyudenij. No tut ego podsteregaet
drugaya trudnost'.
Horosho izvestno, chto pri ispol'zovanii sveta opredelennoj dliny volny
nevozmozhno razlichit' detali, razmery kotoryh men'she dliny volny: nel'zya
narisovat' persidskuyu miniatyuru malyarnoj kist'yu! No ispol'zuya vse bolee
dlinnye volny, nash fizik isportit ocenku polozheniya kazhdoj tochki i vskore
dostignet toj stadii, kogda kazhdaya ocenka budet soderzhat' pogreshnost', ili
neopredelennost', velichina kotoroj sravnima s razmerami vsej ego laboratorii
i prevyshaet ih. Tem samym nash nablyudatel' budet vynuzhden v konce koncov
pojti na kompromiss mezhdu bol'shim chislom nablyudaemyh tochek i
neopredelennost'yu v ocenke polozheniya kazhdoj tochki i ne smozhet poluchit'
tochnuyu traektoriyu - v vide linii v matematicheskom smysle v otlichie ot svoih
klassicheskih kolleg. V luchshem sluchae kvantovyj nablyudatel' poluchit ves'ma
shirokuyu razmazannuyu polosu, i esli on popytaetsya postroit' ponyatie
traektorii, opirayas' na svoj opyt, to ono budet sil'no otlichat'sya ot
klassicheskogo ponyatiya traektorii.
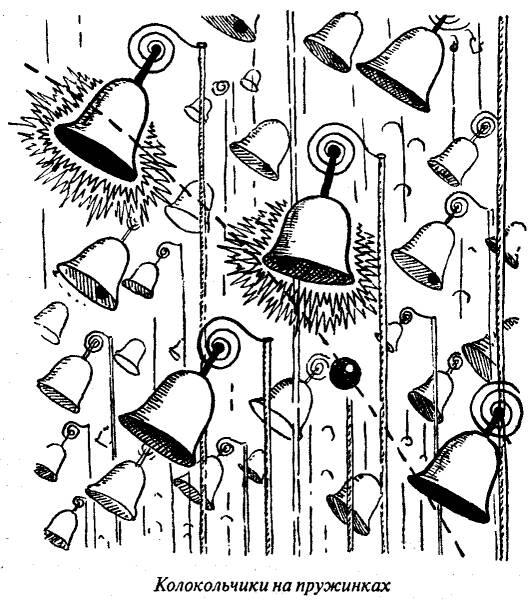 Predlozhennyj vyshe metod postroeniya traektorii byl opticheskim, a teper'
my mozhem isprobovat' druguyu vozmozhnost' i vospol'zovat'sya mehanicheskim
metodom. Dlya etogo nash eksperimentator mozhet postroit' kakoj-nibud'
miniatyurnyj mehanicheskij pribor, naprimer, kolokol'chiki na pruzhinah, kotoryj
budet registrirovat' prohozhdenie material'nyh tel, esli telo prohodit
dostatochno blizko. Bol'shoe chislo takih "kolokol'chikov" on razveshivaet v toj
oblasti prostranstva, gde ozhidaetsya prohozhdenie dvizhushchegosya tela, i "zvon
kolokol'chikov" budet ukazyvat' traektoriyu, opisyvaemuyu telom. V klassicheskoj
fizike "kolokol'chiki" mozhno sdelat' skol' ugodno malymi i chuvstvitel'nymi. V
predel'nom sluchae beskonechno bol'shogo chisla beskonechno malen'kih
kolokol'chikov ponyatie traektorii i v etom sluchae mozhet byt' postroeno s
lyuboj trebuemoj tochnost'yu. Odnako, kak i v predydushchem sluchae, kvantovye
ogranicheniya na mehanicheskie sistemy portyat vse delo. Esli "kolokol'chiki"
slishkom maly, to velichina impul'sa, kotoruyu oni smogut zabrat' u dvizhushchegosya
tela, soglasno formule (3), budet slishkom bol'shoj i dvizhenie okazhetsya sil'no
vozmushchennym dazhe posle togo, kak telo zadenet odin-edinstvennyj kolokol'chik.
Esli zhe kolokol'chiki veliki, to neopredelennost' v polozhenii kazhdogo budet
ochen' bol'shoj. V etom sluchae postroennaya v rezul'tate nablyudeniya
okonchatel'naya traektoriya, kak i v predydushchem sluchae, okazhetsya shirokoj
polosoj!
Boyus', chto vse eti rassuzhdeniya ob eksperimentatore, zhelayushchem nablyudat'
traektoriyu, pokazhutsya vam slishkom special'nymi i vy budete sklonny dumat',
chto esli ispol'zuemye sredstva ne pozvolyayut nashemu nablyudatelyu ocenit'
traektoriyu, to zhelaemyj rezul'tat udastsya poluchit' s pomoshch'yu kakogo-nibud'
drugogo bolee slozhnogo ustrojstva. Odnako ya dolzhen vam napomnit', chto my
rassmatrivali ne konkretnyj eksperiment, vypolnennyj v kakoj-to fizicheskoj
laboratorii, a nekuyu idealizaciyu samogo glavnogo voprosa fizicheskogo
izmereniya. Poskol'ku lyuboe sushchestvuyushchee v nashem mire dejstvie mozhno otnesti
libo k chislu dejstvij polya izlucheniya, libo k chisto mehanicheskim, lyubaya skol'
ugodno slozhnaya shema izmereniya nepremenno svoditsya k elementam, opisyvaemyh
temi dvumya metodami, o kotoryh ya uzhe upominal ran'she - opticheskom i
mehanicheskom, i v konechnom itoge privodit k tomu zhe rezul'tatu. A poskol'ku
ideal'nyj "izmeritel'nyj pribor" mozhet vmestit' ves' fizicheskij mir, my v
konce koncov prihodim k vyvodu, chto v mire, gde dejstvuyut kvantovye zakony,
net ni tochnogo polozheniya, ni traektorii, imeyushchej strogo opredelennuyu formu
linii.
No vernemsya teper' snova k nashemu eksperimentatoru i popytaemsya oblech'
v matematicheskuyu formu ogranicheniya, vytekayushchie iz kvantovyh uslovij. My uzhe
videli, chto v oboih metodah - opticheskom i mehanicheskom - vsegda sushchestvuet
konflikt mezhdu ocenkoj polozheniya i vozmushcheniem skorosti dvizhushchegosya ob容kta.
V opticheskom metode stolknovenie s kvantom sveta (v silu zakona sohraneniya
impul'sa, dejstvuyushchego v klassicheskoj mehanike) porozhdaet neopredelennost' v
impul'se chasticy, sravnimuyu s impul'som samogo kvanta sveta. Takim obrazom,
ispol'zuya formulu (2), zapishem dlya neopredelennosti impul'sa chasticy
Predlozhennyj vyshe metod postroeniya traektorii byl opticheskim, a teper'
my mozhem isprobovat' druguyu vozmozhnost' i vospol'zovat'sya mehanicheskim
metodom. Dlya etogo nash eksperimentator mozhet postroit' kakoj-nibud'
miniatyurnyj mehanicheskij pribor, naprimer, kolokol'chiki na pruzhinah, kotoryj
budet registrirovat' prohozhdenie material'nyh tel, esli telo prohodit
dostatochno blizko. Bol'shoe chislo takih "kolokol'chikov" on razveshivaet v toj
oblasti prostranstva, gde ozhidaetsya prohozhdenie dvizhushchegosya tela, i "zvon
kolokol'chikov" budet ukazyvat' traektoriyu, opisyvaemuyu telom. V klassicheskoj
fizike "kolokol'chiki" mozhno sdelat' skol' ugodno malymi i chuvstvitel'nymi. V
predel'nom sluchae beskonechno bol'shogo chisla beskonechno malen'kih
kolokol'chikov ponyatie traektorii i v etom sluchae mozhet byt' postroeno s
lyuboj trebuemoj tochnost'yu. Odnako, kak i v predydushchem sluchae, kvantovye
ogranicheniya na mehanicheskie sistemy portyat vse delo. Esli "kolokol'chiki"
slishkom maly, to velichina impul'sa, kotoruyu oni smogut zabrat' u dvizhushchegosya
tela, soglasno formule (3), budet slishkom bol'shoj i dvizhenie okazhetsya sil'no
vozmushchennym dazhe posle togo, kak telo zadenet odin-edinstvennyj kolokol'chik.
Esli zhe kolokol'chiki veliki, to neopredelennost' v polozhenii kazhdogo budet
ochen' bol'shoj. V etom sluchae postroennaya v rezul'tate nablyudeniya
okonchatel'naya traektoriya, kak i v predydushchem sluchae, okazhetsya shirokoj
polosoj!
Boyus', chto vse eti rassuzhdeniya ob eksperimentatore, zhelayushchem nablyudat'
traektoriyu, pokazhutsya vam slishkom special'nymi i vy budete sklonny dumat',
chto esli ispol'zuemye sredstva ne pozvolyayut nashemu nablyudatelyu ocenit'
traektoriyu, to zhelaemyj rezul'tat udastsya poluchit' s pomoshch'yu kakogo-nibud'
drugogo bolee slozhnogo ustrojstva. Odnako ya dolzhen vam napomnit', chto my
rassmatrivali ne konkretnyj eksperiment, vypolnennyj v kakoj-to fizicheskoj
laboratorii, a nekuyu idealizaciyu samogo glavnogo voprosa fizicheskogo
izmereniya. Poskol'ku lyuboe sushchestvuyushchee v nashem mire dejstvie mozhno otnesti
libo k chislu dejstvij polya izlucheniya, libo k chisto mehanicheskim, lyubaya skol'
ugodno slozhnaya shema izmereniya nepremenno svoditsya k elementam, opisyvaemyh
temi dvumya metodami, o kotoryh ya uzhe upominal ran'she - opticheskom i
mehanicheskom, i v konechnom itoge privodit k tomu zhe rezul'tatu. A poskol'ku
ideal'nyj "izmeritel'nyj pribor" mozhet vmestit' ves' fizicheskij mir, my v
konce koncov prihodim k vyvodu, chto v mire, gde dejstvuyut kvantovye zakony,
net ni tochnogo polozheniya, ni traektorii, imeyushchej strogo opredelennuyu formu
linii.
No vernemsya teper' snova k nashemu eksperimentatoru i popytaemsya oblech'
v matematicheskuyu formu ogranicheniya, vytekayushchie iz kvantovyh uslovij. My uzhe
videli, chto v oboih metodah - opticheskom i mehanicheskom - vsegda sushchestvuet
konflikt mezhdu ocenkoj polozheniya i vozmushcheniem skorosti dvizhushchegosya ob容kta.
V opticheskom metode stolknovenie s kvantom sveta (v silu zakona sohraneniya
impul'sa, dejstvuyushchego v klassicheskoj mehanike) porozhdaet neopredelennost' v
impul'se chasticy, sravnimuyu s impul'som samogo kvanta sveta. Takim obrazom,
ispol'zuya formulu (2), zapishem dlya neopredelennosti impul'sa chasticy
 (4)
Pamyatuya o tom, chto neopredelennost' polozheniya chasticy opredelyaetsya
dlinoj volny ((del'ta)q = lyambda), poluchaem
(4)
Pamyatuya o tom, chto neopredelennost' polozheniya chasticy opredelyaetsya
dlinoj volny ((del'ta)q = lyambda), poluchaem
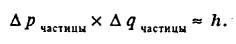 (5)
V mehanicheskom metode impul's stanovitsya neopredelennym na velichinu,
peredavaemuyu "kolokol'chikom". Ispol'zuya nashu formulu (3) i pomnya o tom, chto
v etom sluchae neopredelennost' polozheniya opredelyaetsya razmerami kolokol'chika
((del'ta)q = l), my prihodim k toj zhe okonchatel'noj formule, chto i v
predydushchem sluchae. Sootnoshenie (5), vpervye vyvedennoe nemeckim fizikom
Vernerom Gejzenbergom, opisyvaet fundamental'nuyu neopredelennost', sleduyushchuyu
iz kvantovoj teorii: _chem tochnee opredeleno polozhenie, tem neopredelennee
skorost', i naoborot_.
Tak kak impul's est' proizvedenie massy dvizhushchejsya chasticy i ee
skorosti, my mozhem zapisat', chto
(5)
V mehanicheskom metode impul's stanovitsya neopredelennym na velichinu,
peredavaemuyu "kolokol'chikom". Ispol'zuya nashu formulu (3) i pomnya o tom, chto
v etom sluchae neopredelennost' polozheniya opredelyaetsya razmerami kolokol'chika
((del'ta)q = l), my prihodim k toj zhe okonchatel'noj formule, chto i v
predydushchem sluchae. Sootnoshenie (5), vpervye vyvedennoe nemeckim fizikom
Vernerom Gejzenbergom, opisyvaet fundamental'nuyu neopredelennost', sleduyushchuyu
iz kvantovoj teorii: _chem tochnee opredeleno polozhenie, tem neopredelennee
skorost', i naoborot_.
Tak kak impul's est' proizvedenie massy dvizhushchejsya chasticy i ee
skorosti, my mozhem zapisat', chto
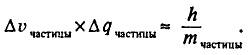 (6)
Dlya tel, s kotorymi nam obychno prihoditsya imet' delo, neopredelennost'
(6) do smeshnogo mala. Tak, v sluchae legkoj pylinki s massoj 0,0000001 g i
polozhenie, i skorost' mogut byt' izmereny s tochnost'yu 0,00000001 %! Odnako v
sluchae elektrona (s massoj 10^-27 g) proizvedenie (del'ta)u * (del'ta)q
dostigaet velichiny poryadka 100. Vnutri atoma skorost' elektrona neobhodimo
opredelyat' po krajnej mere v predelah +-10^8 sm/s, v protivnom sluchae
elektron okazhetsya vne atoma. |to daet dlya polozheniya elektrona
neopredelennost' 10^8 sm, t. e. neopredelennost', sovpadayushchuyu s polnymi
razmerami atoma. Takim obrazom, "orbita" elektrona v atome rasplyvaetsya do
takoj stepeni, chto "tolshchina" traektorii stanovitsya ravnoj ee "radiusu" -
_elektron okazyvaetsya odnovremenno vsyudu vokrug yadra_.
Na protyazhenii poslednih dvadcati minut ya pytalsya narisovat' vam kartinu
razrushitel'nyh posledstvij nashej kritiki klassicheskih predstavlenij o
dvizhenii. Izyashchnye i chetko opredelennye klassicheskie ponyatiya okazyvayutsya
vdrebezgi razbitymi i ustupayut mesto tomu, chto ya nazval by besformennoj
razmaznej. Estestvenno, vy mozhete sprosit' menya, kak fiziki sobirayutsya
opisyvat' kakie-nibud' yavleniya, esli kvantovyj mir bukval'no zahlestyvayut
volny okeana neopredelennosti. Otvet sostoit v tom, chto do sih por nam
udalos' lish' razrushit' klassicheskie ponyatiya, no my eshche ne prishli k tochnoj
formulirovke novyh ponyatij.
Zajmemsya etim teper'. YAsno, chto my ne mozhem, voobshche govorya, opredelit'
polozhenie material'noj chasticy s pomoshch'yu material'noj tochki, a traektoriyu ee
dvizheniya - s pomoshch'yu matematicheskoj linii, poskol'ku v kvantovom mire vse
ob容kty rasplyvayutsya. Nam neobhodimo obratit'sya k drugim metodam opisaniya,
dayushchim, tak skazat', "plotnost' razmazni" v razlichnyh tochkah prostranstva.
Matematicheski eto oznachaet, chto my ispol'zuem nepreryvnye funkcii (takie
kak, naprimer, v gidromehanike), a fizicheski trebuet, chtoby pri opisanii
kvantovogo mira my upotreblyali takie oboroty rechi, kak "etot ob容kt v
osnovnom nahoditsya zdes', chastichno tam i dazhe von tam" ili "eta moneta na
75% nahoditsya v moem karmane i na 25% - v vashem". YA ponimayu, chto takie
utverzhdeniya kazhutsya vam dikimi, no v nashej povsednevnoj zhizni iz-za malosti
kvantovoj postoyannoj v nih net nadobnosti. No esli vy voznamerites' izuchat'
atomnuyu fiziku, to ya nastoyatel'no rekomenduyu vam predvaritel'no privyknut' k
takogo roda vyrazheniyam.
Schitayu svoim dolgom predosterech' vas ot oshibochnogo predstavleniya o tom,
budto funkciya, opisyvayushchaya "plotnost' prebyvaniya" ob容kta v razlichnyh tochkah
prostranstva, obladaet fizicheskoj real'nost'yu v nashem obychnom trehmernom
prostranstve. Dejstvitel'no, esli my opisyvaem povedenie, naprimer, dvuh
chastic, to nam neobhodimo otvetit' na vopros, nahoditsya li odna chastica v
odnom meste i, odnovremenno, vtoraya chastica v drugom meste. Dlya etogo nam
neobhodima funkciya shesti peremennyh (koordinat dvuh chastic), kotoruyu
nevozmozhno "lokalizovat'" v trehmernom prostranstve. Dlya opisaniya bolee
slozhnyh sistem nam ponadobilis' by funkcii eshche bol'shego chisla peremennyh. V
etom smysle "kvantovo-mehanicheskaya funkciya" analogichna "potencial'noj
funkcii", ili "potencialu", sistemy chastic v klassicheskoj mehanike ili
"entropii" sistemy v statisticheskoj mehanike: ona tol'ko opisyvaet dvizhenie
i pozvolyaet nam predskazyvat' rezul'tat lyubogo konkretnogo dvizheniya pri
dannyh usloviyah. Fizicheskaya real'nost' ostaetsya za chasticami, dvizhenie
kotoryh my opisyvaem.
Funkciya, kotoraya opisyvaet, kakaya "dolya" chasticy ili sistemy chastic
prisutstvuet v razlichnyh mestah prostranstva, trebuet special'nogo
matematicheskogo oboznacheniya. Sleduya |rvinu SHredingeru, kotoryj pervym
napisal uravnenie, opredelyayushchee povedenie takoj funkcii, ee stali oboznachat'
(6)
Dlya tel, s kotorymi nam obychno prihoditsya imet' delo, neopredelennost'
(6) do smeshnogo mala. Tak, v sluchae legkoj pylinki s massoj 0,0000001 g i
polozhenie, i skorost' mogut byt' izmereny s tochnost'yu 0,00000001 %! Odnako v
sluchae elektrona (s massoj 10^-27 g) proizvedenie (del'ta)u * (del'ta)q
dostigaet velichiny poryadka 100. Vnutri atoma skorost' elektrona neobhodimo
opredelyat' po krajnej mere v predelah +-10^8 sm/s, v protivnom sluchae
elektron okazhetsya vne atoma. |to daet dlya polozheniya elektrona
neopredelennost' 10^8 sm, t. e. neopredelennost', sovpadayushchuyu s polnymi
razmerami atoma. Takim obrazom, "orbita" elektrona v atome rasplyvaetsya do
takoj stepeni, chto "tolshchina" traektorii stanovitsya ravnoj ee "radiusu" -
_elektron okazyvaetsya odnovremenno vsyudu vokrug yadra_.
Na protyazhenii poslednih dvadcati minut ya pytalsya narisovat' vam kartinu
razrushitel'nyh posledstvij nashej kritiki klassicheskih predstavlenij o
dvizhenii. Izyashchnye i chetko opredelennye klassicheskie ponyatiya okazyvayutsya
vdrebezgi razbitymi i ustupayut mesto tomu, chto ya nazval by besformennoj
razmaznej. Estestvenno, vy mozhete sprosit' menya, kak fiziki sobirayutsya
opisyvat' kakie-nibud' yavleniya, esli kvantovyj mir bukval'no zahlestyvayut
volny okeana neopredelennosti. Otvet sostoit v tom, chto do sih por nam
udalos' lish' razrushit' klassicheskie ponyatiya, no my eshche ne prishli k tochnoj
formulirovke novyh ponyatij.
Zajmemsya etim teper'. YAsno, chto my ne mozhem, voobshche govorya, opredelit'
polozhenie material'noj chasticy s pomoshch'yu material'noj tochki, a traektoriyu ee
dvizheniya - s pomoshch'yu matematicheskoj linii, poskol'ku v kvantovom mire vse
ob容kty rasplyvayutsya. Nam neobhodimo obratit'sya k drugim metodam opisaniya,
dayushchim, tak skazat', "plotnost' razmazni" v razlichnyh tochkah prostranstva.
Matematicheski eto oznachaet, chto my ispol'zuem nepreryvnye funkcii (takie
kak, naprimer, v gidromehanike), a fizicheski trebuet, chtoby pri opisanii
kvantovogo mira my upotreblyali takie oboroty rechi, kak "etot ob容kt v
osnovnom nahoditsya zdes', chastichno tam i dazhe von tam" ili "eta moneta na
75% nahoditsya v moem karmane i na 25% - v vashem". YA ponimayu, chto takie
utverzhdeniya kazhutsya vam dikimi, no v nashej povsednevnoj zhizni iz-za malosti
kvantovoj postoyannoj v nih net nadobnosti. No esli vy voznamerites' izuchat'
atomnuyu fiziku, to ya nastoyatel'no rekomenduyu vam predvaritel'no privyknut' k
takogo roda vyrazheniyam.
Schitayu svoim dolgom predosterech' vas ot oshibochnogo predstavleniya o tom,
budto funkciya, opisyvayushchaya "plotnost' prebyvaniya" ob容kta v razlichnyh tochkah
prostranstva, obladaet fizicheskoj real'nost'yu v nashem obychnom trehmernom
prostranstve. Dejstvitel'no, esli my opisyvaem povedenie, naprimer, dvuh
chastic, to nam neobhodimo otvetit' na vopros, nahoditsya li odna chastica v
odnom meste i, odnovremenno, vtoraya chastica v drugom meste. Dlya etogo nam
neobhodima funkciya shesti peremennyh (koordinat dvuh chastic), kotoruyu
nevozmozhno "lokalizovat'" v trehmernom prostranstve. Dlya opisaniya bolee
slozhnyh sistem nam ponadobilis' by funkcii eshche bol'shego chisla peremennyh. V
etom smysle "kvantovo-mehanicheskaya funkciya" analogichna "potencial'noj
funkcii", ili "potencialu", sistemy chastic v klassicheskoj mehanike ili
"entropii" sistemy v statisticheskoj mehanike: ona tol'ko opisyvaet dvizhenie
i pozvolyaet nam predskazyvat' rezul'tat lyubogo konkretnogo dvizheniya pri
dannyh usloviyah. Fizicheskaya real'nost' ostaetsya za chasticami, dvizhenie
kotoryh my opisyvaem.
Funkciya, kotoraya opisyvaet, kakaya "dolya" chasticy ili sistemy chastic
prisutstvuet v razlichnyh mestah prostranstva, trebuet special'nogo
matematicheskogo oboznacheniya. Sleduya |rvinu SHredingeru, kotoryj pervym
napisal uravnenie, opredelyayushchee povedenie takoj funkcii, ee stali oboznachat'
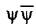 .
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej
.
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej 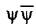 -funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
-funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
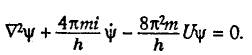 (7)
Zdes' U oznachaet potencial sil, dejstvuyushchih na nashu chasticu (s massoj
m), i porozhdaet opredelennoe reshenie zadachi o dvizhenii chasticy pri lyubom
zadannom raspredelenii sily. "Volnovoe uravnenie SHredingera" (tak prinyato
nazyvat' vyvedennoe SHredingerom fundamental'noe uravnenie) pozvolilo fizikam
v posleduyushchie sorok let ego sushchestvovaniya postroit' naibolee polnuyu i
logicheski neprotivorechivuyu kartinu yavlenij, proishodyashchih v mire atomov.
Nekotorye iz vas, dolzhno byt', udivlyayutsya, pochemu ya do sih por ni razu
ne upotrebil slovo "matrica", kotoroe chasto prihoditsya slyshat' v svyazi s
kvantovoj teoriej. Dolzhen priznat'sya, chto lichno ya pitayu sil'nuyu nepriyazn' k
matricam i predpochitayu obhodit'sya bez nih. No chtoby ne ostavlyat' vas v
absolyutnom nevedenii otnositel'no etogo matematicheskogo apparata kvantovoj
teorii, ya skazhu o matricah neskol'ko slov. Kak vy uzhe znaete, dvizhenie
chasticy ili slozhnoj mehanicheskoj sistemy vsegda mozhno opisat' s pomoshch'yu
nekotoryh nepreryvnyh volnovyh funkcij. |ti funkcii chasto byvayut ochen'
slozhnymi i predstavimy v vide nabora iz nekotorogo chisla bolee prostyh
kolebanij (tak nazyvaemyh "sobstvennyh funkcij") podobno tomu, kak slozhnyj
zvuk mozhno sostavit' iz nekotorogo chisla prostyh garmonicheskih tonov.
Slozhnoe dvizhenie mozhno opisyvat', zadavaya amplitudy ego razlichnyh komponent.
Poskol'ku chislo komponent (obertonov) beskonechno, my vypisyvaem beskonechnuyu
tablicu amplitud vida
(7)
Zdes' U oznachaet potencial sil, dejstvuyushchih na nashu chasticu (s massoj
m), i porozhdaet opredelennoe reshenie zadachi o dvizhenii chasticy pri lyubom
zadannom raspredelenii sily. "Volnovoe uravnenie SHredingera" (tak prinyato
nazyvat' vyvedennoe SHredingerom fundamental'noe uravnenie) pozvolilo fizikam
v posleduyushchie sorok let ego sushchestvovaniya postroit' naibolee polnuyu i
logicheski neprotivorechivuyu kartinu yavlenij, proishodyashchih v mire atomov.
Nekotorye iz vas, dolzhno byt', udivlyayutsya, pochemu ya do sih por ni razu
ne upotrebil slovo "matrica", kotoroe chasto prihoditsya slyshat' v svyazi s
kvantovoj teoriej. Dolzhen priznat'sya, chto lichno ya pitayu sil'nuyu nepriyazn' k
matricam i predpochitayu obhodit'sya bez nih. No chtoby ne ostavlyat' vas v
absolyutnom nevedenii otnositel'no etogo matematicheskogo apparata kvantovoj
teorii, ya skazhu o matricah neskol'ko slov. Kak vy uzhe znaete, dvizhenie
chasticy ili slozhnoj mehanicheskoj sistemy vsegda mozhno opisat' s pomoshch'yu
nekotoryh nepreryvnyh volnovyh funkcij. |ti funkcii chasto byvayut ochen'
slozhnymi i predstavimy v vide nabora iz nekotorogo chisla bolee prostyh
kolebanij (tak nazyvaemyh "sobstvennyh funkcij") podobno tomu, kak slozhnyj
zvuk mozhno sostavit' iz nekotorogo chisla prostyh garmonicheskih tonov.
Slozhnoe dvizhenie mozhno opisyvat', zadavaya amplitudy ego razlichnyh komponent.
Poskol'ku chislo komponent (obertonov) beskonechno, my vypisyvaem beskonechnuyu
tablicu amplitud vida
 (8)
Nad takimi tablicami mozhno proizvodit' matematicheskie operacii po
sravnitel'no prostym pravilam. Kazhdaya takaya tablica i nazyvaetsya "matricej",
i nekotorye fiziki vmesto togo, chtoby imet' delo neposredstvenno s volnovymi
funkciyami, predpochitayut operirovat' s matricami. Takaya "matrichnaya mehanika",
kak ee inogda nazyvayut, predstavlyaet soboj ne bolee chem matematicheskuyu
modifikaciyu obychnoj "volnovoj mehaniki". V nashih lekciyah, posvyashchennyh
glavnym obrazom principial'nym voprosam, bylo by izlishne vhodit' v eti
problemy bolee podrobno.
Ochen' zhal', chto nedostatok vremeni ne pozvolyaet mne rasskazat' vam o
dal'nejshem progresse kvantovoj teorii v svyazi s teoriej otnositel'nosti. |ta
glava v razvitii kvantovoj teorii, svyazannaya glavnym obrazom s rabotami
britanskogo fizika Polya Adriena Morisa Diraka, privodit ko mnogim
interesnejshim problemam i stala osnovoj nekotoryh chrezvychajno vazhnyh
eksperimental'nyh otkrytij. Vozmozhno, kogda-nibud' v drugoj raz ya eshche
vernus' k etim problemam, a poka ya dolzhen ostanovit'sya. Nadeyus', chto
prochitannaya mnoj seriya lekcij pozvolila vam sostavit' bolee yasnoe
predstavlenie o sovremennoj koncepcii fizicheskogo mira i probudila v vas
interes k dal'nejshim nauchnym zanyatiyam.
Glava 8
Kvantovye dzhungli
Na sleduyushchee utro mister Tompkins eshche nezhilsya v posteli, kak vdrug
pochuvstvoval, chto v komnate est' eshche kto-to. Oglyadevshis' vokrug, on
obnaruzhil svoego starogo druga professora. Tot sidel v kresle, utknuvshis' v
rasstelennuyu na kolenyah kartu i vnimatel'no izuchal ee.
- Tak vy so mnoj? - sprosil professor, podnimaya golovu.
- A kuda eto vy sobralis'? - pointeresovalsya mister Tompkins, razmyshlyaya
nad tem, kakim obrazom professor okazalsya u nego v komnate.
- Razumeetsya, dlya togo chtoby polyubovat'sya na slonov i drugih obitatelej
dzhunglej. Vladelec bil'yardnoj, gde my s vami nedavno pobyvali, soobshchil mne
po sekretu, otkuda on beret slonovuyu kost' dlya svoih bil'yardnyh sharov.
Vidite rajon, kotoryj ya obvel na karte krasnym karandashom? Imeyutsya osnovaniya
polagat', chto vnutri nego vse podchineno kvantovym zakonam s ochen' bol'shoj
kvantovoj postoyannoj. Mestnye zhiteli schitayut, chto v teh krayah poselilis'
d'yavoly, i ya boyus', chto nam budet ochen' trudno najti sebe provodnika. No
esli vy hotite otpravit'sya so mnoj v put', vam nado potoraplivat'sya. Sudno
othodit cherez chas, a nam eshche nuzhno po doroge v port zaehat' za serom
Richardom.
- A kto eto ser Richard? - sprosil mister Tompkins.
- Kak, vy nikogda ne slyhali o nem? - professor byl yavno izumlen. - Ser
Richard izvestnyj ohotnik na tigrov. On reshil otpravit'sya vmeste s nami,
kogda ya obeshchal emu interesnuyu ohotu.
Na prichal uchastniki ekspedicii pribyli kak raz vovremya dlya togo, chtoby
nablyudat' za pogruzkoj na bort sudna gruza iz neskol'kih dlinnyh yashchikov s
ruzh'yami sera Richarda i special'nymi pulyami, izgotovlennymi iz svinca,
kotoryj professor poluchil ot upravlyayushchego svincovymi rudnikami,
raspolozhennymi nepodaleku ot kvantovyh dzhunglej. Mister Tompkins eshche
raskladyval veshchi v kayute, kogda mernaya vibraciya korpusa sudna vozvestila
emu, chto parohod otoshel ot prichala. V morskom puteshestvii vsegda est' nechto
neotrazimo privlekatel'noe, i mister Tompkins ne zametil, kak ih sudno
prishvartovalos' v ocharovatel'nom vostochnom gorode - blizhajshem k tainstvennym
kvantovym dzhunglyam naselennom punkte.
- Dlya puteshestviya po sushe nam nuzhno priobresti slona, - ob座avil
professor. - Ne dumayu, chto kto-nibud' iz mestnyh zhitelej risknet otpravit'sya
s nami, poetomu upravlyat' slonom pridetsya nam samim. Polagayu, chto vy, mister
Tompkins, prekrasno spravites' s etoj zadachej. YA budu slishkom pogloshchen
nauchnymi nablyudeniyami, a ser Richard dolzhen budet upravlyat'sya so vsem
ohotnich'im snaryazheniem.
Na dushe u mistera Tompkinsa bylo ochen' nespokojno, kogda pridya na
slonovyj rynok, raspolozhennyj na okraine goroda, on uvidel ogromnyh
zhivotnyh, odnim iz kotoryh emu predstoyalo upravlyat'. Ser Richard, velikolepno
razbiravshijsya v slonah, vybral krasivogo krupnogo slona i sprosil u
vladel'ca, skol'ko tot hochet za zhivotnoe.
- Hrap hanvek o hobot ham. Hagori ho, o Hohohohi, - otvetil tuzemec,
obnazhiv v ulybke oslepitel'no belye zuby.
- On prosit za nego ujmu deneg, - perevel ser Richard, - no govorit, chto
ego slon iz kvantovyh dzhunglej i poetomu stoit dorozhe. Tak kak, kupim etogo
slona?
- Nepremenno, - skazal professor. - Na parohode mne dovelos' slyshat',
chto slony inogda zahodyat iz kvantovyh territorij i tuzemcy ih lovyat. Takie
slony gorazdo luchshe svoih sorodichej iz drugih oblastej, i sejchas nam prosto
povezlo, chto my mozhem kupit' zhivotnoe, kotoroe chuvstvuet sebya v kvantovyh
dzhunglyah, kak doma.
Mister Tompkins osmotrel slona so vseh storon. CHto i govorit', eto bylo
ochen' krasivoe, ogromnoe zhivotnoe, odnako, mister Tomtgkins ne zametil v
povadkah slona kakih-libo otlichij po sravneniyu s temi slonami, kotoryh emu
dovodilos' videt' v zooparke.
- Vy govorite, chto eto kvantovyj slon, a dlya menya on vpolne obychnyj
slon i vedet sebya ne tak zanyatno, kak bil'yardnye shary, sdelannye iz bivnej
nekotoryh iz ego sorodichej. Naprimer, pochemu on ne rasplyvaetsya po vsem
napravleniyam? - obratilsya mister Tompkins k professoru.
- Vy medlenno shvatyvaete sut' dela, - zametil professor. - Slon ne
rasplyvaetsya iz-za svoej ochen' bol'shoj massy. Nekotoroe vremya nazad ya uzhe
ob座asnyal vam, chto neopredelennost' v polozhenii i skorosti zavisit ot massy.
CHem bol'she massa, tem men'she neopredelennost'. Imenno poetomu kvantovye
zakony ne nablyudayutsya v obychnom mire dazhe dlya takih legkih tel, kak pylinki,
no stanovyatsya vpolne zametnymi dlya elektronov, kotorye v milliardy
milliardov raz legche pylinok. No v kvantovyh dzhunglyah kvantovaya postoyannaya
gorazdo bol'she, no vse zhe nedostatochno velika, chtoby porozhdat' porazitel'nye
effekty v povedenii stol' tyazhelogo zhivotnogo, kak slon. Neopredelennost' v
polozhenii kvantovogo slona mozhno zametit', tol'ko esli pristal'no vglyadet'sya
v ego ochertaniya. Vozmozhno, vy zametili, chto poverhnost' slonovoj kozhi ne
vpolne opredelenna i kazhetsya neskol'ko neotchetlivo vidimoj. So vremenem eta
neopredelennost' uvelichivaetsya ochen' medlenno. Mne kazhetsya, chto imenno s
etim obstoyatel'stvom svyazana mestnaya legenda, budto u staryh slonov iz
kvantovyh dzhunglej dlinnaya sherst'. YA polagayu, chto na ne stol' krupnyh
zhivotnyh, obitayushchih v kvantovyh dzhunglyah, zamechatel'nye kvantovye effekty
budut bolee zametnymi.
- Horosho, chto v etu ekspediciyu my otpravlyaemsya ne verhom na loshadyah, -
podumal mister Tompkins. - Ved' esli by my vzdumali otpravit'sya v kvantovye
dzhungli na loshadyah, ya nikogda ne mog by skazat' s uverennost'yu, gde moya
loshad' - u menya pod sedlom ili v sleduyushchej doline.
Posle togo, kak professor i ser Richard so svoimi ruzh'yami vzgromozdilis'
v korzinu, ukreplennuyu na spine slona, a mister Tompkins v novoj dlya sebya
dolzhnosti pogonshchika zanyal svoe mesto na shee slona, krepko szhimaya v ruke
nekoe podobie bagra - strekalo, kotorym _nastoyashchie_ pogonshchiki upravlyayut
svoim podopechnym; ekspediciya tronulas' v put' k tainstvennym dzhunglyam.
Ot zhitelej goroda nashi puteshestvenniki uznali, chto dobrat'sya do
dzhunglej mozhno primerno za chas, i mister Tompkins, izo vseh sil pytayas'
sohranit' ravnovesie mezhdu ushami slona, voznamerilsya s pol'zoj ispol'zovat'
vremya, chtoby porassprosit' u professora o kvantovyh yavleniyah.
- Skazhite, pozhalujsta, - nachal mister Tompkins, povernuvshis' k
professoru, - _pochemu_ tela s maloj massoj vedut sebya stol' neobychno i kak
mozhno istolkovat' s tochki zreniya obychnogo zdravogo smysla tu kvantovuyu
postoyannuyu, o kotoroj vy vse vremya govorite?
- O, - voskliknul professor, - ponyat' eto ne tak uzh trudno. Neobychnoe
povedenie vseh ob容ktov v kvantovom mire ob座asnyaetsya prosto tem, chto vy na
nih smotrite.
- Oni nastol'ko stydlivy? - ulybnulsya mister Tompkins.
- "Stydlivy" - ne to slovo, - surovo otvetstvoval professor. - Sut'
dela v tom, chto vsyakij raz, proizvodya lyuboe nablyudenie, vy nepremenno
vozmushchaete dvizhenie nablyudaemogo ob容kta. Raz vy uznaete chto-to o dvizhenii
kakogo-to tela, to eto oznachaet, chto dvizhushcheesya telo proizvelo kakoe-to
dejstvie na vashi organy chuvstv ili na pribor, kotoryj vy ispol'zovali pri
nablyudenii. V silu ravenstva dejstviya i protivodejstviya my prihodim k
zaklyucheniyu, chto vash izmeritel'nyj pribor takzhe vozdejstvoval na telo i, tak
skazat', "isportil" ego dvizhenie, vvedya neopredelennost' v polozhenie i
skorost' tela.
- Esli by ya tronul bil'yardnyj shar pal'cem, to, konechno, vnes by
vozmushchenie v ego dvizhenie, - nedoumenno proiznes mister Tompkins. - No ya
tol'ko posmotrel na nego. Neuzheli etogo dostatochno, chtoby vozmutit' dvizhenie
bil'yardnogo shara?
- Razumeetsya, vpolne dostatochno! Vy zhe ne mozhete videt' bil'yardnyj shar
v kromeshnoj t'me. A esli vy vynesete shar na svet, to luchi sveta,
otrazhayushchiesya ot shara i delayushchie ego vidimym, vozdejstvuyut na nego (my
govorim o takom vozdejstvii kak o "davlenii sveta") i "portyat" dvizhenie
shara.
- A chto esli ya vospol'zuyus' ochen' tonkimi i ochen' chuvstvitel'nymi
priborami? Razve ne smogu ya sdelat' vozdejstvie moih priborov na dvizhushcheesya
telo prenebrezhimo malym?
- Imenno tak my schitali, kogda u nas byla tol'ko klassicheskaya fizika,
do otkrytiya _kvanta dejstviya_. No v nachale XX stoletiya stalo yasno, chto
dejstvie na lyuboj ob容kt ne mozhet byt' nizvedeno do urovnya nizhe
opredelennogo predela, nazyvaemogo kvantovoj postoyannoj i oboznachaemogo
simvolom h. V obychnom mire kvant dejstviya ochen' mal; v obychnyh edinicah on
vyrazhaetsya chislom s dvadcat'yu sem'yu nulyami posle desyatichnoj zapyatoj. Kvant
dejstviya stanovitsya sushchestvennym tol'ko dlya takih legkih chastic, kak
elektrony: iz-za ih ochen' maloj massy na dvizhenii takih chastic zametno
skazyvayutsya i ochen' slabye vozdejstviya. V kvantovyh dzhunglyah, k kotorym my
sejchas priblizhaemsya, kvant dejstviya ochen' velik. |to grubyj mir, v kotorom
delikatnye dejstviya nevozmozhny. Esli kto-nibud' v takom mire popytaetsya
pogladit' kotenka, to tot libo voobshche ne oshchutit nikakoj laski, libo ego sheya
budet slomana pri pervom zhe prikosnovenii.
- Vse eto horosho, - zadumchivo progovoril mister Tompkins, - no vedut li
tela sebya prilichno, t.e. tak, kak obychno prinyato dumat', kogda na nih nikto
ne smotrit?
- Kogda na tela nikto ne smotrit, - otvetil professor, - nikto ne mozhet
skazat', kak oni sebya vedut. Vash vopros ne imeet fizicheskogo smysla.
- Dolzhen priznat'sya, - zametil mister Tompkins, - chto vse eto izryadno
smahivaet na filosofiyu, a ne na fiziku.
- Mozhete nazyvat' eto filosofiej, - professor byl yavno zadet, - no, v
dejstvitel'nosti, rech' idet o fundamental'nom principe sovremennoj fiziki -
_nikogda ne govorit' o tom, chego ne znaesh'_. Vsya sovremennaya fizicheskaya
teoriya osnovana na etom principe, mezhdu tem, kak filosofy obychno upuskayut
ego iz vidu. Naprimer, znamenityj nemeckij filosof Kant provel nemalo
vremeni, razmyshlyaya o svojstvah tel, ne takih, kakimi oni "vidyatsya nam", a
takih, kakie oni est' " v sebe". Dlya sovremennogo fizika imeyut smysl tol'ko
tak nazyvaemye "nablyudaemye" (t. e. principial'no nablyudaemye svojstva), i
vsya sovremennaya fizika osnovana na otnosheniyah mezhdu nablyudaemymi svojstvami.
To, chto nevozmozhno nablyudat', horosho tol'ko dlya prazdnyh razmyshlenij: vy
mozhete pridumyvat' chto ugodno, i plody vashih razmyshlenij nel'zya ni proverit'
(t. e. ubedit'sya v ih sushchestvovanii), ni vospol'zovat'sya imi. Dolzhen
skazat', chto...
(8)
Nad takimi tablicami mozhno proizvodit' matematicheskie operacii po
sravnitel'no prostym pravilam. Kazhdaya takaya tablica i nazyvaetsya "matricej",
i nekotorye fiziki vmesto togo, chtoby imet' delo neposredstvenno s volnovymi
funkciyami, predpochitayut operirovat' s matricami. Takaya "matrichnaya mehanika",
kak ee inogda nazyvayut, predstavlyaet soboj ne bolee chem matematicheskuyu
modifikaciyu obychnoj "volnovoj mehaniki". V nashih lekciyah, posvyashchennyh
glavnym obrazom principial'nym voprosam, bylo by izlishne vhodit' v eti
problemy bolee podrobno.
Ochen' zhal', chto nedostatok vremeni ne pozvolyaet mne rasskazat' vam o
dal'nejshem progresse kvantovoj teorii v svyazi s teoriej otnositel'nosti. |ta
glava v razvitii kvantovoj teorii, svyazannaya glavnym obrazom s rabotami
britanskogo fizika Polya Adriena Morisa Diraka, privodit ko mnogim
interesnejshim problemam i stala osnovoj nekotoryh chrezvychajno vazhnyh
eksperimental'nyh otkrytij. Vozmozhno, kogda-nibud' v drugoj raz ya eshche
vernus' k etim problemam, a poka ya dolzhen ostanovit'sya. Nadeyus', chto
prochitannaya mnoj seriya lekcij pozvolila vam sostavit' bolee yasnoe
predstavlenie o sovremennoj koncepcii fizicheskogo mira i probudila v vas
interes k dal'nejshim nauchnym zanyatiyam.
Glava 8
Kvantovye dzhungli
Na sleduyushchee utro mister Tompkins eshche nezhilsya v posteli, kak vdrug
pochuvstvoval, chto v komnate est' eshche kto-to. Oglyadevshis' vokrug, on
obnaruzhil svoego starogo druga professora. Tot sidel v kresle, utknuvshis' v
rasstelennuyu na kolenyah kartu i vnimatel'no izuchal ee.
- Tak vy so mnoj? - sprosil professor, podnimaya golovu.
- A kuda eto vy sobralis'? - pointeresovalsya mister Tompkins, razmyshlyaya
nad tem, kakim obrazom professor okazalsya u nego v komnate.
- Razumeetsya, dlya togo chtoby polyubovat'sya na slonov i drugih obitatelej
dzhunglej. Vladelec bil'yardnoj, gde my s vami nedavno pobyvali, soobshchil mne
po sekretu, otkuda on beret slonovuyu kost' dlya svoih bil'yardnyh sharov.
Vidite rajon, kotoryj ya obvel na karte krasnym karandashom? Imeyutsya osnovaniya
polagat', chto vnutri nego vse podchineno kvantovym zakonam s ochen' bol'shoj
kvantovoj postoyannoj. Mestnye zhiteli schitayut, chto v teh krayah poselilis'
d'yavoly, i ya boyus', chto nam budet ochen' trudno najti sebe provodnika. No
esli vy hotite otpravit'sya so mnoj v put', vam nado potoraplivat'sya. Sudno
othodit cherez chas, a nam eshche nuzhno po doroge v port zaehat' za serom
Richardom.
- A kto eto ser Richard? - sprosil mister Tompkins.
- Kak, vy nikogda ne slyhali o nem? - professor byl yavno izumlen. - Ser
Richard izvestnyj ohotnik na tigrov. On reshil otpravit'sya vmeste s nami,
kogda ya obeshchal emu interesnuyu ohotu.
Na prichal uchastniki ekspedicii pribyli kak raz vovremya dlya togo, chtoby
nablyudat' za pogruzkoj na bort sudna gruza iz neskol'kih dlinnyh yashchikov s
ruzh'yami sera Richarda i special'nymi pulyami, izgotovlennymi iz svinca,
kotoryj professor poluchil ot upravlyayushchego svincovymi rudnikami,
raspolozhennymi nepodaleku ot kvantovyh dzhunglej. Mister Tompkins eshche
raskladyval veshchi v kayute, kogda mernaya vibraciya korpusa sudna vozvestila
emu, chto parohod otoshel ot prichala. V morskom puteshestvii vsegda est' nechto
neotrazimo privlekatel'noe, i mister Tompkins ne zametil, kak ih sudno
prishvartovalos' v ocharovatel'nom vostochnom gorode - blizhajshem k tainstvennym
kvantovym dzhunglyam naselennom punkte.
- Dlya puteshestviya po sushe nam nuzhno priobresti slona, - ob座avil
professor. - Ne dumayu, chto kto-nibud' iz mestnyh zhitelej risknet otpravit'sya
s nami, poetomu upravlyat' slonom pridetsya nam samim. Polagayu, chto vy, mister
Tompkins, prekrasno spravites' s etoj zadachej. YA budu slishkom pogloshchen
nauchnymi nablyudeniyami, a ser Richard dolzhen budet upravlyat'sya so vsem
ohotnich'im snaryazheniem.
Na dushe u mistera Tompkinsa bylo ochen' nespokojno, kogda pridya na
slonovyj rynok, raspolozhennyj na okraine goroda, on uvidel ogromnyh
zhivotnyh, odnim iz kotoryh emu predstoyalo upravlyat'. Ser Richard, velikolepno
razbiravshijsya v slonah, vybral krasivogo krupnogo slona i sprosil u
vladel'ca, skol'ko tot hochet za zhivotnoe.
- Hrap hanvek o hobot ham. Hagori ho, o Hohohohi, - otvetil tuzemec,
obnazhiv v ulybke oslepitel'no belye zuby.
- On prosit za nego ujmu deneg, - perevel ser Richard, - no govorit, chto
ego slon iz kvantovyh dzhunglej i poetomu stoit dorozhe. Tak kak, kupim etogo
slona?
- Nepremenno, - skazal professor. - Na parohode mne dovelos' slyshat',
chto slony inogda zahodyat iz kvantovyh territorij i tuzemcy ih lovyat. Takie
slony gorazdo luchshe svoih sorodichej iz drugih oblastej, i sejchas nam prosto
povezlo, chto my mozhem kupit' zhivotnoe, kotoroe chuvstvuet sebya v kvantovyh
dzhunglyah, kak doma.
Mister Tompkins osmotrel slona so vseh storon. CHto i govorit', eto bylo
ochen' krasivoe, ogromnoe zhivotnoe, odnako, mister Tomtgkins ne zametil v
povadkah slona kakih-libo otlichij po sravneniyu s temi slonami, kotoryh emu
dovodilos' videt' v zooparke.
- Vy govorite, chto eto kvantovyj slon, a dlya menya on vpolne obychnyj
slon i vedet sebya ne tak zanyatno, kak bil'yardnye shary, sdelannye iz bivnej
nekotoryh iz ego sorodichej. Naprimer, pochemu on ne rasplyvaetsya po vsem
napravleniyam? - obratilsya mister Tompkins k professoru.
- Vy medlenno shvatyvaete sut' dela, - zametil professor. - Slon ne
rasplyvaetsya iz-za svoej ochen' bol'shoj massy. Nekotoroe vremya nazad ya uzhe
ob座asnyal vam, chto neopredelennost' v polozhenii i skorosti zavisit ot massy.
CHem bol'she massa, tem men'she neopredelennost'. Imenno poetomu kvantovye
zakony ne nablyudayutsya v obychnom mire dazhe dlya takih legkih tel, kak pylinki,
no stanovyatsya vpolne zametnymi dlya elektronov, kotorye v milliardy
milliardov raz legche pylinok. No v kvantovyh dzhunglyah kvantovaya postoyannaya
gorazdo bol'she, no vse zhe nedostatochno velika, chtoby porozhdat' porazitel'nye
effekty v povedenii stol' tyazhelogo zhivotnogo, kak slon. Neopredelennost' v
polozhenii kvantovogo slona mozhno zametit', tol'ko esli pristal'no vglyadet'sya
v ego ochertaniya. Vozmozhno, vy zametili, chto poverhnost' slonovoj kozhi ne
vpolne opredelenna i kazhetsya neskol'ko neotchetlivo vidimoj. So vremenem eta
neopredelennost' uvelichivaetsya ochen' medlenno. Mne kazhetsya, chto imenno s
etim obstoyatel'stvom svyazana mestnaya legenda, budto u staryh slonov iz
kvantovyh dzhunglej dlinnaya sherst'. YA polagayu, chto na ne stol' krupnyh
zhivotnyh, obitayushchih v kvantovyh dzhunglyah, zamechatel'nye kvantovye effekty
budut bolee zametnymi.
- Horosho, chto v etu ekspediciyu my otpravlyaemsya ne verhom na loshadyah, -
podumal mister Tompkins. - Ved' esli by my vzdumali otpravit'sya v kvantovye
dzhungli na loshadyah, ya nikogda ne mog by skazat' s uverennost'yu, gde moya
loshad' - u menya pod sedlom ili v sleduyushchej doline.
Posle togo, kak professor i ser Richard so svoimi ruzh'yami vzgromozdilis'
v korzinu, ukreplennuyu na spine slona, a mister Tompkins v novoj dlya sebya
dolzhnosti pogonshchika zanyal svoe mesto na shee slona, krepko szhimaya v ruke
nekoe podobie bagra - strekalo, kotorym _nastoyashchie_ pogonshchiki upravlyayut
svoim podopechnym; ekspediciya tronulas' v put' k tainstvennym dzhunglyam.
Ot zhitelej goroda nashi puteshestvenniki uznali, chto dobrat'sya do
dzhunglej mozhno primerno za chas, i mister Tompkins, izo vseh sil pytayas'
sohranit' ravnovesie mezhdu ushami slona, voznamerilsya s pol'zoj ispol'zovat'
vremya, chtoby porassprosit' u professora o kvantovyh yavleniyah.
- Skazhite, pozhalujsta, - nachal mister Tompkins, povernuvshis' k
professoru, - _pochemu_ tela s maloj massoj vedut sebya stol' neobychno i kak
mozhno istolkovat' s tochki zreniya obychnogo zdravogo smysla tu kvantovuyu
postoyannuyu, o kotoroj vy vse vremya govorite?
- O, - voskliknul professor, - ponyat' eto ne tak uzh trudno. Neobychnoe
povedenie vseh ob容ktov v kvantovom mire ob座asnyaetsya prosto tem, chto vy na
nih smotrite.
- Oni nastol'ko stydlivy? - ulybnulsya mister Tompkins.
- "Stydlivy" - ne to slovo, - surovo otvetstvoval professor. - Sut'
dela v tom, chto vsyakij raz, proizvodya lyuboe nablyudenie, vy nepremenno
vozmushchaete dvizhenie nablyudaemogo ob容kta. Raz vy uznaete chto-to o dvizhenii
kakogo-to tela, to eto oznachaet, chto dvizhushcheesya telo proizvelo kakoe-to
dejstvie na vashi organy chuvstv ili na pribor, kotoryj vy ispol'zovali pri
nablyudenii. V silu ravenstva dejstviya i protivodejstviya my prihodim k
zaklyucheniyu, chto vash izmeritel'nyj pribor takzhe vozdejstvoval na telo i, tak
skazat', "isportil" ego dvizhenie, vvedya neopredelennost' v polozhenie i
skorost' tela.
- Esli by ya tronul bil'yardnyj shar pal'cem, to, konechno, vnes by
vozmushchenie v ego dvizhenie, - nedoumenno proiznes mister Tompkins. - No ya
tol'ko posmotrel na nego. Neuzheli etogo dostatochno, chtoby vozmutit' dvizhenie
bil'yardnogo shara?
- Razumeetsya, vpolne dostatochno! Vy zhe ne mozhete videt' bil'yardnyj shar
v kromeshnoj t'me. A esli vy vynesete shar na svet, to luchi sveta,
otrazhayushchiesya ot shara i delayushchie ego vidimym, vozdejstvuyut na nego (my
govorim o takom vozdejstvii kak o "davlenii sveta") i "portyat" dvizhenie
shara.
- A chto esli ya vospol'zuyus' ochen' tonkimi i ochen' chuvstvitel'nymi
priborami? Razve ne smogu ya sdelat' vozdejstvie moih priborov na dvizhushcheesya
telo prenebrezhimo malym?
- Imenno tak my schitali, kogda u nas byla tol'ko klassicheskaya fizika,
do otkrytiya _kvanta dejstviya_. No v nachale XX stoletiya stalo yasno, chto
dejstvie na lyuboj ob容kt ne mozhet byt' nizvedeno do urovnya nizhe
opredelennogo predela, nazyvaemogo kvantovoj postoyannoj i oboznachaemogo
simvolom h. V obychnom mire kvant dejstviya ochen' mal; v obychnyh edinicah on
vyrazhaetsya chislom s dvadcat'yu sem'yu nulyami posle desyatichnoj zapyatoj. Kvant
dejstviya stanovitsya sushchestvennym tol'ko dlya takih legkih chastic, kak
elektrony: iz-za ih ochen' maloj massy na dvizhenii takih chastic zametno
skazyvayutsya i ochen' slabye vozdejstviya. V kvantovyh dzhunglyah, k kotorym my
sejchas priblizhaemsya, kvant dejstviya ochen' velik. |to grubyj mir, v kotorom
delikatnye dejstviya nevozmozhny. Esli kto-nibud' v takom mire popytaetsya
pogladit' kotenka, to tot libo voobshche ne oshchutit nikakoj laski, libo ego sheya
budet slomana pri pervom zhe prikosnovenii.
- Vse eto horosho, - zadumchivo progovoril mister Tompkins, - no vedut li
tela sebya prilichno, t.e. tak, kak obychno prinyato dumat', kogda na nih nikto
ne smotrit?
- Kogda na tela nikto ne smotrit, - otvetil professor, - nikto ne mozhet
skazat', kak oni sebya vedut. Vash vopros ne imeet fizicheskogo smysla.
- Dolzhen priznat'sya, - zametil mister Tompkins, - chto vse eto izryadno
smahivaet na filosofiyu, a ne na fiziku.
- Mozhete nazyvat' eto filosofiej, - professor byl yavno zadet, - no, v
dejstvitel'nosti, rech' idet o fundamental'nom principe sovremennoj fiziki -
_nikogda ne govorit' o tom, chego ne znaesh'_. Vsya sovremennaya fizicheskaya
teoriya osnovana na etom principe, mezhdu tem, kak filosofy obychno upuskayut
ego iz vidu. Naprimer, znamenityj nemeckij filosof Kant provel nemalo
vremeni, razmyshlyaya o svojstvah tel, ne takih, kakimi oni "vidyatsya nam", a
takih, kakie oni est' " v sebe". Dlya sovremennogo fizika imeyut smysl tol'ko
tak nazyvaemye "nablyudaemye" (t. e. principial'no nablyudaemye svojstva), i
vsya sovremennaya fizika osnovana na otnosheniyah mezhdu nablyudaemymi svojstvami.
To, chto nevozmozhno nablyudat', horosho tol'ko dlya prazdnyh razmyshlenij: vy
mozhete pridumyvat' chto ugodno, i plody vashih razmyshlenij nel'zya ni proverit'
(t. e. ubedit'sya v ih sushchestvovanii), ni vospol'zovat'sya imi. Dolzhen
skazat', chto...
 V etot moment uzhasnyj rev potryas vozduh. Slon ostanovilsya kak vkopannyj
tak vnezapno, chto mister Tompkins chut' ne svalilsya. Ogromnaya staya neskol'ko
razmazannyh tigrov napala na slona, vyprygnuv iz zasady so vseh storon. Ser
Richard shvatil svoe ruzh'e i, pricelivshis' blizhajshemu tigru mezhdu glaz,
spustil kurok. V sleduyushchij moment mister Tompkins otchetlivo uslyshal, kak ser
Richard proburchal sebe pod nos nekoe krepkoe vyrazhenie, prinyatoe sredi
ohotnikov. Eshche by! Vystrel byl metkim, no pulya proshla skvoz' golovu tigra,
ne prichiniv tomu ni malejshego vreda!
- Strelyaj eshche! - zakrichal professor. - Ne cel'tes'! Postarajtes'
sozdat' vokrug sebya kak mozhno bol'shuyu plotnost' ognya! Na nas napal tol'ko
odin tigr, no on raspredelen vokrug nashego slona, i nash edinstvennyj shans na
spasenie sostoit v tom, chtoby podnyat' gamil'tonian.
Professor shvatil drugoe ruzh'e, i grohot vystrelov smeshalsya s revom
kvantovogo tigra. Misteru Tompkinsu pokazalos', chto proshla celaya vechnost'
prezhde, chem ves' etot uzhasnyj shum zatih. Odna iz pul' "popala v cel'", i k
velichajshemu udivleniyu mistera Tomtpsinsa tigr, vnezapno prevrativshijsya v
odnogo-edinstvennogo titra, byl s siloj otbroshen nazad, i ego mertvoe telo,
opisav dugu v vozduhe, prizemlilos' gde-to za mayachivshej v otdalenii
pal'movoj roshchej.
- A kto etot Gamil'tonian? - sprosil mister Tompkins, kogda vse nemnogo
uspokoilos'. - Znamenityj ohotnik, kotorogo vy hoteli podnyat' iz mogily,
chtoby on spas nas?
- O, proshu velikodushno prostit' menya! - skazal professor. - V pylu
bitvy ya pereshel na nauchnuyu terminologiyu, kotoruyu vy ne ponimaete!
Gamil'tonianom prinyato nazyvat' matematicheskoe vyrazhenie, opisyvayushchee
kvantovoe vzaimodejstvie mezhdu dvumya telami. Ono poluchilo svoe nazvanie v
chest' irlandskogo matematika Gamil'tona, kotoryj pervym nachal ispol'zovat'
etu matematicheskuyu formu. YA hotel skazat', chto, vypuskaya kak mozhno bol'she
pul', my mozhem uvelichit' veroyatnost' vzaimodejstviya mezhdu pulej i telom
tigra. V kvantovom mire vy ne mozhete tochno pricelit'sya i byt' uvereny, chto
popadete v cel'. Iz-za rasplyvaniya puli i celi vsegda sushchestvuet lish'
otlichnaya ot nulya veroyatnost' popadaniya v cel', no eta veroyatnost' nikogda ne
ravna edinice. V nashem sluchae my vypustili po krajnej mere tridcat' pul',
prezhde chem dejstvitel'no popali v tigra, i togda dejstvie puli okazalos'
stol' sil'nym, chto tigra otbrosilo daleko nazad. To zhe samoe, tol'ko v
men'shih masshtabah, proishodit i v nashem privychnom mire. Kak ya uzhe upominal,
v obychnom mire, chtoby zametit' nechto podobnoe, neobhodimo issledovat'
povedenie takih malyh chastic, kak elektrony. Vozmozhno, vam prihodilos'
slyshat' o tom, chto kazhdyj atom sostoit iz sravnitel'no tyazhelogo yadra i
neskol'kih elektronov, obrashchayushchihsya vokrug nego. Snachala prinyato bylo
dumat', chto dvizhenie elektronov vokrug yadra sovershenno analogichno dvizheniyu
planet vokrug Solnca, no bolee glubokij analiz pokazal, chto obychnye ponyatiya,
otnosyashchiesya k dvizheniyu, slishkom gruby dlya takoj miniatyurnoj sistemy, kak
atom. Dejstviya, igrayushchie vazhnuyu rol' vnutri atoma, po poryadku velichiny
sravnimy s elementarnym kvantom dejstviya, i poetomu vsya kartina v celom
sil'no rasplyvaetsya. Dvizhenie elektrona vokrug atomnogo yadra vo mnogih
otnosheniyah analogichno dvizheniyu nashego kvantovogo tigra, kotoryj v odinochku
okruzhil nashego slona so vseh storon.
- A ne strelyal li kto-nibud' v elektron tak, kak my strelyali v tigra? -
sprosil mister Tompkins.
- Strelyali i ne raz! YAdro samo ispuskaet inogda kvanty sveta vysokoj
energii, ili, chto to zhe, elementarnye porcii dejstviya sveta. V elektron
mozhno vystrelit' i snaruzhi atoma, osveshchaya atom puchkom sveta. Pri etom vse
proizojdet tak zhe, kak s tigrom: mnogie kvanty sveta projdut cherez to mesto,
gde nahoditsya elektron, ne okazav na togo ni malejshego dejstviya, poka,
nakonec, odin iz kvantov sveta ne stolknetsya s elektronom i ne vyb'et ego iz
atoma. Na kvantovuyu sistemu nel'zya vozdejstvovat' chut'-chut'; ona libo voobshche
ne ispytyvaet nikakogo vozdejstviya, libo preterpevaet v rezul'tate
vozdejstviya sil'nye izmeneniya.
- Kak tot neschastnyj kotenok, kotorogo nel'zya prilaskat' v kvantovom
mire, ne riskuya nanesti emu smertel'noe uvech'e, - zaklyuchil mister Tompkins.
- Vzglyanite von tuda! Gazeli! Mnozhestvo gazelej! - voskliknul ser
Richard, podnimaya svoe ruzh'e. I, dejstvitel'no, ogromnoe stado gazelej
pokazalos' iz bambukovoj roshchi.
- Dressirovannye gazeli, - podumal mister Tompkins. - Begut stroem, kak
soldaty na parade. Hotel by ya znat', uzh ne kvantovyj li eto effekt?
V etot moment uzhasnyj rev potryas vozduh. Slon ostanovilsya kak vkopannyj
tak vnezapno, chto mister Tompkins chut' ne svalilsya. Ogromnaya staya neskol'ko
razmazannyh tigrov napala na slona, vyprygnuv iz zasady so vseh storon. Ser
Richard shvatil svoe ruzh'e i, pricelivshis' blizhajshemu tigru mezhdu glaz,
spustil kurok. V sleduyushchij moment mister Tompkins otchetlivo uslyshal, kak ser
Richard proburchal sebe pod nos nekoe krepkoe vyrazhenie, prinyatoe sredi
ohotnikov. Eshche by! Vystrel byl metkim, no pulya proshla skvoz' golovu tigra,
ne prichiniv tomu ni malejshego vreda!
- Strelyaj eshche! - zakrichal professor. - Ne cel'tes'! Postarajtes'
sozdat' vokrug sebya kak mozhno bol'shuyu plotnost' ognya! Na nas napal tol'ko
odin tigr, no on raspredelen vokrug nashego slona, i nash edinstvennyj shans na
spasenie sostoit v tom, chtoby podnyat' gamil'tonian.
Professor shvatil drugoe ruzh'e, i grohot vystrelov smeshalsya s revom
kvantovogo tigra. Misteru Tompkinsu pokazalos', chto proshla celaya vechnost'
prezhde, chem ves' etot uzhasnyj shum zatih. Odna iz pul' "popala v cel'", i k
velichajshemu udivleniyu mistera Tomtpsinsa tigr, vnezapno prevrativshijsya v
odnogo-edinstvennogo titra, byl s siloj otbroshen nazad, i ego mertvoe telo,
opisav dugu v vozduhe, prizemlilos' gde-to za mayachivshej v otdalenii
pal'movoj roshchej.
- A kto etot Gamil'tonian? - sprosil mister Tompkins, kogda vse nemnogo
uspokoilos'. - Znamenityj ohotnik, kotorogo vy hoteli podnyat' iz mogily,
chtoby on spas nas?
- O, proshu velikodushno prostit' menya! - skazal professor. - V pylu
bitvy ya pereshel na nauchnuyu terminologiyu, kotoruyu vy ne ponimaete!
Gamil'tonianom prinyato nazyvat' matematicheskoe vyrazhenie, opisyvayushchee
kvantovoe vzaimodejstvie mezhdu dvumya telami. Ono poluchilo svoe nazvanie v
chest' irlandskogo matematika Gamil'tona, kotoryj pervym nachal ispol'zovat'
etu matematicheskuyu formu. YA hotel skazat', chto, vypuskaya kak mozhno bol'she
pul', my mozhem uvelichit' veroyatnost' vzaimodejstviya mezhdu pulej i telom
tigra. V kvantovom mire vy ne mozhete tochno pricelit'sya i byt' uvereny, chto
popadete v cel'. Iz-za rasplyvaniya puli i celi vsegda sushchestvuet lish'
otlichnaya ot nulya veroyatnost' popadaniya v cel', no eta veroyatnost' nikogda ne
ravna edinice. V nashem sluchae my vypustili po krajnej mere tridcat' pul',
prezhde chem dejstvitel'no popali v tigra, i togda dejstvie puli okazalos'
stol' sil'nym, chto tigra otbrosilo daleko nazad. To zhe samoe, tol'ko v
men'shih masshtabah, proishodit i v nashem privychnom mire. Kak ya uzhe upominal,
v obychnom mire, chtoby zametit' nechto podobnoe, neobhodimo issledovat'
povedenie takih malyh chastic, kak elektrony. Vozmozhno, vam prihodilos'
slyshat' o tom, chto kazhdyj atom sostoit iz sravnitel'no tyazhelogo yadra i
neskol'kih elektronov, obrashchayushchihsya vokrug nego. Snachala prinyato bylo
dumat', chto dvizhenie elektronov vokrug yadra sovershenno analogichno dvizheniyu
planet vokrug Solnca, no bolee glubokij analiz pokazal, chto obychnye ponyatiya,
otnosyashchiesya k dvizheniyu, slishkom gruby dlya takoj miniatyurnoj sistemy, kak
atom. Dejstviya, igrayushchie vazhnuyu rol' vnutri atoma, po poryadku velichiny
sravnimy s elementarnym kvantom dejstviya, i poetomu vsya kartina v celom
sil'no rasplyvaetsya. Dvizhenie elektrona vokrug atomnogo yadra vo mnogih
otnosheniyah analogichno dvizheniyu nashego kvantovogo tigra, kotoryj v odinochku
okruzhil nashego slona so vseh storon.
- A ne strelyal li kto-nibud' v elektron tak, kak my strelyali v tigra? -
sprosil mister Tompkins.
- Strelyali i ne raz! YAdro samo ispuskaet inogda kvanty sveta vysokoj
energii, ili, chto to zhe, elementarnye porcii dejstviya sveta. V elektron
mozhno vystrelit' i snaruzhi atoma, osveshchaya atom puchkom sveta. Pri etom vse
proizojdet tak zhe, kak s tigrom: mnogie kvanty sveta projdut cherez to mesto,
gde nahoditsya elektron, ne okazav na togo ni malejshego dejstviya, poka,
nakonec, odin iz kvantov sveta ne stolknetsya s elektronom i ne vyb'et ego iz
atoma. Na kvantovuyu sistemu nel'zya vozdejstvovat' chut'-chut'; ona libo voobshche
ne ispytyvaet nikakogo vozdejstviya, libo preterpevaet v rezul'tate
vozdejstviya sil'nye izmeneniya.
- Kak tot neschastnyj kotenok, kotorogo nel'zya prilaskat' v kvantovom
mire, ne riskuya nanesti emu smertel'noe uvech'e, - zaklyuchil mister Tompkins.
- Vzglyanite von tuda! Gazeli! Mnozhestvo gazelej! - voskliknul ser
Richard, podnimaya svoe ruzh'e. I, dejstvitel'no, ogromnoe stado gazelej
pokazalos' iz bambukovoj roshchi.
- Dressirovannye gazeli, - podumal mister Tompkins. - Begut stroem, kak
soldaty na parade. Hotel by ya znat', uzh ne kvantovyj li eto effekt?
 Gruppa gazelej bystro priblizhalas' k slonu, na kotorom vossedali nashi
puteshestvenniki, i ser Richard izgotovilsya bylo strelyat', kak vdrug professor
ostanovil ego.
- Ne trat'te ponaprasnu vashi ohotnich'i pripasy, - skazal professor. -
Ochen' malo shansov popast' v zhivotnoe, kogda ono dvizhetsya v difrakcionnoj
kartine.
- Pochemu vy govorite ne o zhivotnyh, a ob odnom zhivotnom, udivlenno
sprosil ser Richard. - Zdes' po krajnej mere neskol'ko dyuzhin gazelej!
- Vy gluboko zabluzhdaetes', - vozrazil professor. - Zdes' pered nami
tol'ko odna malen'kaya gazel', kotoraya, ispugavshis' chego-to, mchitsya skvoz'
bambukovuyu roshchu. Delo v tom, chto "rasplyvanie" vseh tel obladaet odnim
svojstvom, analogichnym svojstvu obychnogo sveta: prohodya cherez pravil'nuyu
sistemu otverstij ("reshetku"), naprimer mezhdu stvolami bambuka v roshche, ono
porozhdaet yavlenie difrakcii, o kotorom vam, veroyatno, prihodilos' slyshat' v
shkole. Poetomu my govorim o volnovom haraktere materii.
No ni ser Richard, ni mister Tompkins ne mogli vspomnit', chto zhe,
sobstvenno govorya, oznachaet zagadochnoe slovo "difrakciya" i razgovor
oborvalsya.
Uglubivshis' v debri kvantovyh dzhunglej, nashi puteshestvenniki
povstrechali mnozhestvo drugih interesnejshih yavlenij, naprimer, poznakomilis'
s kvantovymi moskitami. Opredelit' mestonahozhdenie etih nasekomyh v
prostranstve bylo pochti nevozmozhno iz-za ih maloj massy. Ochen' zabavny byli
kvantovye obez'yany.
No vot vperedi pokazalos' chto-to napominayushchee tuzemnoe selenie.
- YA ne znal, chto v etih mestah zhivut lyudi, - zametil professor. - Sudya
po shumu, u nih kakoe-to prazdnestvo. Vy tol'ko prislushajtes' k neumolkaemomu
zvonu kolokol'chikov.
Razlichit' otdel'nye figury tuzemcev, ispolnyavshih vokrug bol'shogo kostra
kakoj-to dikij tanec, bylo ochen' trudno. Iz tolpy, kuda ni glyan', vsyudu
podnimalis' temno-korichnevye ruki s kolokol'chikami vseh razmerov. Kogda
puteshestvenniki priblizilis', vse, vklyuchaya hizhiny i okruzhavshie selenie
bol'shie derev'ya, nachalo rasplyvat'sya. Zvon kolokol'chikov stal nevynosimym
dlya mistera Tompkinsa. On protyanul ruku, shvatil chto-to i otbrosil v
storonu. Budil'nik razbil stakan s vodoj, stoyavshij na nochnom stolike, i
potok holodnoj vody privel mistera Tompkinsa v chuvstvo. On vskochil i
prinyalsya bystro odevat'sya. CHerez polchasa emu nuzhno bylo byt' v banke.
Glava 9
Demon Maksvella
Uchastvuya na protyazhenii mnogih mesyacev v neveroyatnyh priklyucheniyah, v
hode kotoryh professor ne upuskal udobnogo sluchaya posvyatit' mistera
Tompkinsa v tajny fiziki, mister Tompkins vse bolee pronikalsya ocharovaniem
miss Mod. Nakonec, nastal den', kogda mister Tompkins, zaikayas' i krasneya ot
smushcheniya, robko predlozhil miss Mod ruku i serdce. Predlozhenie bylo s
radost'yu prinyato, i vskore mister Tompkins i miss Mod stali muzhem i zhenoj. V
novoj dlya sebya roli testya professor schital svoej nepremennoj obyazannost'yu
vsyacheski sposobstvovat' rasshireniyu poznanij svoego zyatya v fizike i znakomit'
ego s novejshimi dostizheniyami etoj uvlekatel'noj nauki.
Odnazhdy mister i missis Tompkins, s udobstvom ustroivshis' v kreslah,
predavalis' voskresnomu otdyhu v svoej uyutnoj kvartirke. Missis Tompkins s
golovoj pogruzilas' v izuchenie zhurnala mod "Vogue", a ee suprug s uvlecheniem
chital stat'yu v zhurnale "Esquire" {Esli byt' tochnym, to sleduet skazat', chto
vnimanie mistera Tompkinsa privlekla stat'ya v yanvarskom nomere etogo zhurnala
za 1940 g.}.
- Podumat' tol'ko! - vnezapno voskliknul mister Tompkins. -
Okazyvaetsya, v azartnyh igrah sushchestvuyut besproigryshnye strategii!
- Siril, neuzheli ty vser'ez dumaesh', chto takoe vozmozhno? - sprosila
missis Tompkins, zadumchivo podnimaya glaza ot prikovavshih ee vnimanie stranic
modnogo zhurnala. - Pomnitsya, papa ne raz govoril nam o tom, chto v azartnyh
igrah besproigryshnyh strategij net i byt' i ne mozhet.
Gruppa gazelej bystro priblizhalas' k slonu, na kotorom vossedali nashi
puteshestvenniki, i ser Richard izgotovilsya bylo strelyat', kak vdrug professor
ostanovil ego.
- Ne trat'te ponaprasnu vashi ohotnich'i pripasy, - skazal professor. -
Ochen' malo shansov popast' v zhivotnoe, kogda ono dvizhetsya v difrakcionnoj
kartine.
- Pochemu vy govorite ne o zhivotnyh, a ob odnom zhivotnom, udivlenno
sprosil ser Richard. - Zdes' po krajnej mere neskol'ko dyuzhin gazelej!
- Vy gluboko zabluzhdaetes', - vozrazil professor. - Zdes' pered nami
tol'ko odna malen'kaya gazel', kotoraya, ispugavshis' chego-to, mchitsya skvoz'
bambukovuyu roshchu. Delo v tom, chto "rasplyvanie" vseh tel obladaet odnim
svojstvom, analogichnym svojstvu obychnogo sveta: prohodya cherez pravil'nuyu
sistemu otverstij ("reshetku"), naprimer mezhdu stvolami bambuka v roshche, ono
porozhdaet yavlenie difrakcii, o kotorom vam, veroyatno, prihodilos' slyshat' v
shkole. Poetomu my govorim o volnovom haraktere materii.
No ni ser Richard, ni mister Tompkins ne mogli vspomnit', chto zhe,
sobstvenno govorya, oznachaet zagadochnoe slovo "difrakciya" i razgovor
oborvalsya.
Uglubivshis' v debri kvantovyh dzhunglej, nashi puteshestvenniki
povstrechali mnozhestvo drugih interesnejshih yavlenij, naprimer, poznakomilis'
s kvantovymi moskitami. Opredelit' mestonahozhdenie etih nasekomyh v
prostranstve bylo pochti nevozmozhno iz-za ih maloj massy. Ochen' zabavny byli
kvantovye obez'yany.
No vot vperedi pokazalos' chto-to napominayushchee tuzemnoe selenie.
- YA ne znal, chto v etih mestah zhivut lyudi, - zametil professor. - Sudya
po shumu, u nih kakoe-to prazdnestvo. Vy tol'ko prislushajtes' k neumolkaemomu
zvonu kolokol'chikov.
Razlichit' otdel'nye figury tuzemcev, ispolnyavshih vokrug bol'shogo kostra
kakoj-to dikij tanec, bylo ochen' trudno. Iz tolpy, kuda ni glyan', vsyudu
podnimalis' temno-korichnevye ruki s kolokol'chikami vseh razmerov. Kogda
puteshestvenniki priblizilis', vse, vklyuchaya hizhiny i okruzhavshie selenie
bol'shie derev'ya, nachalo rasplyvat'sya. Zvon kolokol'chikov stal nevynosimym
dlya mistera Tompkinsa. On protyanul ruku, shvatil chto-to i otbrosil v
storonu. Budil'nik razbil stakan s vodoj, stoyavshij na nochnom stolike, i
potok holodnoj vody privel mistera Tompkinsa v chuvstvo. On vskochil i
prinyalsya bystro odevat'sya. CHerez polchasa emu nuzhno bylo byt' v banke.
Glava 9
Demon Maksvella
Uchastvuya na protyazhenii mnogih mesyacev v neveroyatnyh priklyucheniyah, v
hode kotoryh professor ne upuskal udobnogo sluchaya posvyatit' mistera
Tompkinsa v tajny fiziki, mister Tompkins vse bolee pronikalsya ocharovaniem
miss Mod. Nakonec, nastal den', kogda mister Tompkins, zaikayas' i krasneya ot
smushcheniya, robko predlozhil miss Mod ruku i serdce. Predlozhenie bylo s
radost'yu prinyato, i vskore mister Tompkins i miss Mod stali muzhem i zhenoj. V
novoj dlya sebya roli testya professor schital svoej nepremennoj obyazannost'yu
vsyacheski sposobstvovat' rasshireniyu poznanij svoego zyatya v fizike i znakomit'
ego s novejshimi dostizheniyami etoj uvlekatel'noj nauki.
Odnazhdy mister i missis Tompkins, s udobstvom ustroivshis' v kreslah,
predavalis' voskresnomu otdyhu v svoej uyutnoj kvartirke. Missis Tompkins s
golovoj pogruzilas' v izuchenie zhurnala mod "Vogue", a ee suprug s uvlecheniem
chital stat'yu v zhurnale "Esquire" {Esli byt' tochnym, to sleduet skazat', chto
vnimanie mistera Tompkinsa privlekla stat'ya v yanvarskom nomere etogo zhurnala
za 1940 g.}.
- Podumat' tol'ko! - vnezapno voskliknul mister Tompkins. -
Okazyvaetsya, v azartnyh igrah sushchestvuyut besproigryshnye strategii!
- Siril, neuzheli ty vser'ez dumaesh', chto takoe vozmozhno? - sprosila
missis Tompkins, zadumchivo podnimaya glaza ot prikovavshih ee vnimanie stranic
modnogo zhurnala. - Pomnitsya, papa ne raz govoril nam o tom, chto v azartnyh
igrah besproigryshnyh strategij net i byt' i ne mozhet.
 - Vzglyani sama, Mod, - predlozhil mister Tompkins, pokazyvaya svoej
supruge stat'yu, kotoruyu on izuchal s takim interesom v techenie poslednego
poluchasa. - YA nichego ne znayu o drugih vyigryshnyh strategiyah, no ta, o
kotoroj govoritsya v etoj stat'e, osnovana na ochen' prostyh matematicheskih
raschetah bez vsyakih obmanov i podvohov, i ya prosto ne znayu, gde zdes' v
rassuzhdeniya mozhet vkrast'sya kakaya-nibud' oshibka. CHtoby vyigrat', nuzhno lish'
vypisat' na listke bumagi chisla
i neukosnitel'no priderzhivat'sya prostyh pravil, privodimyh v toj zhe stat'e.
- Poprobovat', konechno, mozhno, - soglasilas' Mod, nachinaya proyavlyat'
priznaki interesa. - A chto eto za pravila?
- Dlya bol'shej naglyadnosti ya budu sledovat' primeru, privodimomu v
stat'e, ved', kak ty znaesh', uchit'sya luchshe vsego na primerah. V kachestve
illyustracii besproigryshnoj strategii avtor stat'i vybral igru v ruletku. Kak
tebe, dolzhno byt', izvestno, igroki v ruletku delayut stavku na krasnoe ili
na chernoe, t. e., po sushchestvu, kak by zaklyuchayut mezhdu soboj pari
otnositel'no ishoda brosaniya monety - vypadet li moneta vverh orlom ili
reshkoj. YA nachinayu s togo, chto vypisyvayu na listke bumagi chisla
Pervoe pravilo sostoit v tom, chto, delaya stavku, ya dolzhen vylozhit' na
stol chislo fishek, ravnoe summe pervogo i poslednego i vypisannyh chisel (a v
tom sluchae, esli na listke bumagi ostanetsya odno-edinstvennoe chislo, stavka
dolzhna byt' ravna odnomu chislu). Sleduya etomu pravilu, ya dolzhen vylozhit' na
stol chetyre (odnu plyus tri) fishki. Predpolozhim, chto ya stavlyu na krasnoe. Po
pravilam igry, v sluchae vyigrysha mne nuzhno zacherknut' pervoe i poslednee iz
vypisannyh chisel. V nashem primere eto chisla 1 i 3, poetomu, delaya sleduyushchuyu
stavku, ya dolzhen vylozhit' na stol dve fishki (poskol'ku posle vycherkivaniya
chisel 1 i 3 na listke bumagi ostanetsya odno-edinstvennoe chislo 2). V sluchae
proigrysha chislo fishek v predydushchej (proigrannoj) stavke neobhodimo pripisat'
sprava k uzhe vypisannym chislam, a pri opredelenii velichiny sleduyushchej stavki
priderzhivat'sya prezhnego pravila, t. e. vystavit' chislo fishek, ravnoe summe
pervogo i poslednego iz vypisannyh chisel (libo, esli na listke bumagi
ostanetsya tol'ko odno chislo, to etomu chislu).
Predpolozhim, chto ruletka ostanovitsya na chernom i krup'e special'noj
lopatkoj podvinet k sebe vystavlennye mnoj chetyre fishki. Poskol'ku ya
proigral, novyj ryad chisel, vypisannyh na listke bumagi, vyglyadit teper' tak:
(chislo vylozhennyh na stol fishek, ravnoe 4, pripisano sprava). Delaya
sleduyushchuyu stavku, ya dolzhen vylozhit' na stol pyat' (odnu plyus chetyre) fishek. V
stat'e govoritsya, chto i vo vtoroj raz ya snova proigryvayu i chto, nesmotrya na
povtornyj proigrysh, mne nadlezhit priderzhivat'sya prezhnej strategii, t. e.
pripisat' k uzhe vypisannym chislam sprava chislo 5 i vylozhit' na stol shest'
(odnu plyus pyat') fishek.
- Na etot raz ty nepremenno dolzhen vyigrat', - voskliknula Mod, vse
bolee vhodya v azart. - Ne mozhesh' zhe ty vse vremya proigryvat'!
- Eshche kak mogu! - zaveril suprugu mister Tompkins. - V detstve ya
chasten'ko igral s drugimi mal'chishkami v orlyanku - zaklyuchal pari otnositel'no
togo, kakoj storonoj vverh vypadet broshennaya moneta i, hochesh' ver', hochesh'
ne ver', odnazhdy stal svidetelem togo, kak moneta desyat' raz podryad vypala
vverh orlom. No predpolozhim, kak eto delaetsya v stat'e, chto na etot raz ya
dlya raznoobraziya vyigral. V etom sluchae po pravilam igry ya dolzhen poluchit'
svoyu udvoennuyu stavku - dvenadcat' fishek - i po sravneniyu so svoim
pervonachal'nym kapitalom stanu na tri fishki bogache. Sleduya rekomenduemoj
strategii, ya dolzhen vycherknut' chisla 1 i 5, posle chego zapis' na listke
bumagi primet sleduyushchij vid:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto)
Delaya sleduyushchuyu stavku, ya dolzhen vylozhit' na stol shest' (dve plyus
chetyre) fishek.
- Zdes' v stat'e napisano, chto ty snova proigral, - vzdohnula Mod,
zaglyadyvaya v zhurnal cherez plecho muzha. - Znachit, teper' ty dolzhen pripisat' k
chislam sprava shesterku i, delaya sleduyushchuyu stavku, vylozhit' na stol vosem'
fishek. Pravil'no?
- Ty absolyutno prava, no i na etot raz menya podsteregaet proigrysh, i
zapis' na listke bumagi vyglyadit teper' tak:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto), 6, 8
Delaya ocherednuyu stavku, ya dolzhen teper' vylozhit' na stol desyat' (dve
plyus vosem') fishek. V stat'e govoritsya, chto na etot raz ya vyigral. Znachit, ya
dolzhen zacherknut' chisla 2 i 8 i, delaya sleduyushchuyu stavku, vylozhit' na stol
devyat' (tri plyus shest') fishek. No tut menya (tak govoritsya v stat'e) snova
podsteregaet proigrysh.
- Kakoj vse-taki neudachnyj primer! - posetovala, naduv gubki, Mod. - Ty
uspel proigrat' tri raza, a vyigral vsego lish' odin raz!
- Nevazhno, - uspokoil ee mister Tompkins so snishoditel'noj
uverennost'yu fokusnika. - Vse ravno v samom konce cikla vyigrysh ostanetsya za
nami. Poslednij zapusk ruletki prines mne (po utverzhdeniyu avtora stat'i)
proigrysh v devyat' fishek. Poetomu teper' ya dolzhen pripisat' k uzhe vypisannym
chislam sprava devyatku, posle chego zapis' na moem listke budet vyglyadet' tak:
1 (zacherknuto), 2 (zacherknuto), 3, 4, 5 (zacherknuto), 6, 8 (zacherknuto), 9
Na stol mne nuzhno vylozhit' dvenadcat' (tri plyus devyat') fishek. Na etot
raz vyigrysh ostaetsya za mnoj, poetomu ya vycherkivayu chisla 3 i 9 i, delaya
novuyu stavku, vykladyvayu na stol desyat' (chetyre plyus shest') fishek.
Posleduyushchij vyigrysh zavershaet cikl, tak kak vse chisla, vypisannye na listke
bumagi, okazyvayutsya zacherknutymi. YA stal bogache na shest' fishek, hotya vyigral
v ruletku tol'ko chetyre raza, a proigral pyat' raz!
- A ty dejstvitel'no stal na shest' fishek bogache? - nedoverchivo sprosila
Mod.
- V etom ne mozhet byt' nikakih somnenij. Strategiya postroena tak, chto
vsyakij raz po zavershenii cikla ty, hochesh', ne hochesh', nepremenno vyigryvaesh'
shest' fishek. V etom netrudno ubedit'sya s pomoshch'yu neslozhnyh vychislenij,
poetomu ya nazyvayu etu strategiyu matematicheskoj. Kak vidish', ona
besproigryshna. Esli ugodno, mozhesh' vzyat' listok bumagi i proverit' vse
vykladki sama.
- Veryu tebe na slovo, chto strategiya dejstvitel'no besproigryshna, -
zadumchivo skazala Mod, - no ved' shest' fishchek - ne takoj uzh bol'shoj vyigrysh.
- Kak skazat', - vozrazil mister Tompkins, - ved' vyigrysh shesti fishek v
konce kazhdogo cikla _garantirovan_. Povtoryaya proceduru snova i snova
(nachinaya kazhdyj raz s vypisyvaniya chisel 1, 2, 3), ty mozhesh' vyigrat' skol'ko
tvoej dushe ugodno deneg, a eto sovsem neploho.
- |to prosto velikolepno! - soglasilas' Mod. - Teper' ty smozhesh'
ostavit' sluzhbu v banke, my smozhem pereehat' v bolee prostornuyu kvartiru, a
ne dalee, kak vchera, ya videla v vitrine odnogo mehovogo magazina chudesnoe
manto. I stoit ono kakih-nibud'...
- Razumeetsya, my kupim tebe eto manto, dorogaya, - pospeshil zaverit'
zhenu mister Tompkins. - No snachala nam nuzhno kak mozhno skoree otpravit'sya v
Monte-Karlo. Ved' stat'yu, opublikovannuyu v zhurnale "Esquire", prochitaet
mnozhestvo lyudej, i bylo by ochen' dosadno pribyt' v Monte-Karlo lish' dlya
togo, chtoby zastat' tam schastlivchika, kotoryj operedil nas i dovel kazino do
polnogo razoreniya.
- YA sejchas pozvonyu v aeroport, - predlozhila Mod, - i uznayu, kogda
otpravlyaetsya blizhajshij rejs v Monte-Karlo.
- CHto za speshka? - razdalsya v prihozhej znakomyj golos, i v komnatu
voshel staryj professor. Ostanovivshis' v dveryah, on s udivleniem smotrel na
supruzheskuyu chetu Tompkinsov, neskol'ko razgoryachennyh vnezapno otkryvshimisya
pered nimi perspektivami finansovogo blagopoluchiya.
- My namerevaemsya otpravit'sya blizhajshim zhe rejsom v Monte-Karlo i
nadeemsya vernut'sya osnovatel'no razbogatevshimi, - poyasnil mister Tompkins,
podnimayas' iz kresla navstrechu testyu.
- Ah, vot v chem delo! Togda vse ponyatno, - ulybnulsya professor, s
komfortom ustraivayas' v staromodnom kresle u kamina. - U vas est' novaya
besproigryshnaya strategiya?
- No, papa, eta strategiya dejstvitel'no besproigryshnaya, - s uprekom
skazala Mod, vse eshche derzha ruku na telefonnoj trubke.
- Mod sovershenno prava, - podtverdil mister Tompkins, protyagivaya
professoru zhurnal. - Predlagaemaya strategiya prosto ne mozhet ne vyigrat'!
- Tak-taki i ne mozhet? - ironicheski peresprosil professor s ulybkoj. -
Sejchas uvidim!
Beglo oznakomivshis' so stat'ej, professor prodolzhal:
- Otlichitel'naya osobennost' predlagaemoj strategii sostoit v tom, chto
pravilo, reguliruyushchee velichinu stavok, zastavlyaet vas uvelichivat' stavku
posle kazhdogo proigrysha i snizhat' stavku posle kazhdogo vyigrysha.
Sledovatel'no, esli vy budete poperemenno vyigryvat' i proigryvat', prichem
vyigryshi i proigryshi budut cheredovat'sya s absolyutnoj regulyarnost'yu, to vash
kapital budet kolebat'sya, prichem kazhdoe uvelichenie kapitala budet chut'
bol'she ego umen'sheniya. V etom sluchae vy, nesomnenno, dostatochno skoro
stanete millionerom. No, kak vy ponimaete, absolyutnaya regulyarnost'
vstrechaetsya nechasto. V dejstvitel'nosti veroyatnost' poyavleniya pravil'no
chereduyushchejsya posledovatel'nosti vyigryshej i proigryshej stol' zhe mala, kak i
veroyatnost' poyavleniya odinakovoj po dline serii odnih tol'ko vyigryshej.
Takim obrazom, neobhodimo vyyasnit', chto proizojdet, esli neskol'ko vyigryshej
(ili neskol'ko proigryshej) sleduyut podryad drug za drugom. Esli vam, kak
govoryat igroki, ulybnulas' fortuna, to pravila besproigryshnoj strategii
vynuzhdayut vas libo ponizhat', libo po krajnej mere ne povyshat' stavku posle
kazhdogo vyigrysha, poetomu obshchij vyigrysh okazhetsya ne slishkom bol'shim. S
drugoj storony, te zhe pravila zastavlyayut vas posle kazhdogo proigrysha
povyshat' stavku, poetomu polosa neudach mozhet imet' dlya vas katastroficheskie
posledstviya i dazhe pobudit' vas vyjti iz igry. Krivaya kolebanij vashego
kapitala na etot raz sostoit iz neskol'kih medlenno vozrastayushchih uchastkov,
smenyayushchihsya rezkimi spadami. V nachale igry vy s bol'shej veroyatnost'yu
popadaete na dlinnuyu medlenno vozrastayushchuyu chast' krivoj i v techenie
kakogo-to vremeni naslazhdaetes' priyatnym oshchushcheniem togo, chto vash kapital
medlenno, no neuklonno uvelichivaetsya. No esli vy prodolzhaete igru dostatochno
dolgo v nadezhde na poluchenie vse bol'shej i bol'shej pribyli, to sovershenno
neozhidanno dlya vas vnezapno nastupaet rezkij spad, kotoryj mozhet okazat'sya
dostatochno glubokim dlya togo, chtoby vy, sdelav ocherednuyu stavku, poteryali
poslednij penni. Mozhno pokazat', prichem v sovershenno obshchem vide, chto v
predlagaemoj avtorom stat'i strategii, ravno kak i v lyuboj drugoj vyigryshnoj
strategii, veroyatnost' togo, chto krivaya dostignet dvojnoj otmetki, ravna
veroyatnosti dostignut' nulevogo znacheniya. Inache govorya, vy imeete tochno
takoj zhe shans na okonchatel'nyj vyigrysh, kak esli by postavili vse svoi
den'gi na krasnoe ili chernoe i udvoili svoj kapital ili spustili vse, chto
imeli, za odin-edinstvennyj zapusk ruletki. Vse "besproigryshnye" strategii
sposobny lish' prodlit' igru i tem samym dat' vam vozmozhnost' poluchit' za
svoi den'gi bol'she udovol'stviya. No dazhe esli vy ne trebuete ot igry nichego
bol'shego, to i togda igru ne sleduet tak uslozhnyat'. Kak vy znaete, na obode
kolesa ruletki naneseny tridcat' shest' chisel. Nichto ne meshaet postavit' po
fishke na kazhdoe iz chisel, krome kakogo-nibud' odnogo. V etom sluchae vy
imeete tridcat' pyat' shansov iz tridcati shesti na vyigrysh i na to, chto bank
vyplatit vam za odnu fishku bol'she, chem te tridcat' pyat' fishek, kotorye vy,
delaya stavku, vylozhili na stol. Odnako v odnom iz tridcati shesti zapuskov
ruletochnogo kolesa sharik ostanovitsya na tom chisle, na kotoroe vy reshili ne
stavit' svoyu fishku, i vy poteryaete vse svoi tridcat' pyat' fishek. Esli vy
budete priderzhivat'sya takoj strategii v dostatochno prodolzhitel'noj igre, to
krivaya vashego fluktuiruyushchego kapitala budet vyglyadet' tochno tak zhe, kak
krivaya, kotoruyu vy poluchili, sleduya strategii, predlozhennoj zhurnalom.
Razumeetsya, v svoih rassuzhdeniyah ya ishodil iz predpolozheniya o tom, chto
bank ne predprinimaet nikakih mer, chtoby iskusstvenno ponizit' shansy igroka
na vyigrysh. V dejstvitel'nosti zhe na kazhdom ruletochnom kolese, kotoroe mne
prihodilos' videt', byl nul' - "zero", a inogda dazhe dva nulya, chto ponizhaet
shansy igroka na vyigrysh. Takim obrazom, nezavisimo ot vybrannoj igrokom
strategii ego denezhki malo-pomalu perekochevyvayut iz ego karmana v karman
vladel'ca kazino.
- Vy hotite skazat', - udruchenno progovoril mister Tompkins, - chto
nadezhnoj besproigryshnoj strategii ne sushchestvuet i chto vyigrat' den'gi bez
riska proigrat' s veroyatnost'yu chut' bol'she, chem veroyatnost' vyigrysha, prosto
nevozmozhno?
- Imenno eto ya hotel skazat'! - podtverdil dogadku mistera Tompkinsa
professor. - Bolee togo, vyskazannye mnoj soobrazheniya otnosyatsya ne tol'ko k
takim v sushchnosti pustyakovym problemam, kak azartnye igry, no i ko mnogim
razlichnym fizicheskim yavleniyam, kotorye, na pervyj vzglyad, ne imeyut nikakogo
otnosheniya k veroyatnostnym zakonam. Poetomu esli by vam udalos' izobresti
nadezhnuyu vyigryshnuyu strategiyu dlya preodoleniya zakonov sluchaya, to dlya nee
nashlos' by nemalo gorazdo bolee uvlekatel'nyh primenenij, chem igra na den'gi
v kazino. Naprimer, takaya strategiya pozvolila by sozdavat' avtomashiny,
sposobnye sovershat' probegi lyuboj protyazhennosti bez kapli benzina, stroit'
fabriki, rabotayushchie bez uglya, i osushchestvlyat' mnozhestvo drugih ne menee
fantasticheskih proektov.
- YA gde-to chital o takih fantasticheskih mashinah. Kazhetsya, oni
nazyvayutsya vechnymi dvigatelyami? - zametil mister Tompkins. - Esli ya
pravil'no pomnyu, vechnye dvigateli po zamyslu ih sozdatelej dolzhny byli by
rabotat' bez topliva. Prinyato schitat', chto oni nevozmozhny potomu, chto
energiyu nevozmozhno proizvodit' iz nichego. No kak by to ni bylo, vechnye
dvigateli ne imeyut nikakogo otnosheniya k azartnym igram.
- Vy sovershenno pravy, molodoj chelovek, - soglasilsya professor,
neskazanno dovol'nyj tem, chto ego zyat' nachinaet ponemnogu razbirat'sya v
fizike. - Takie vechnye dvigateli (ih prinyato nazyvat' vechnymi dvigatelyami
pervogo roda) ne mogut sushchestvovat' potomu, chto ih sushchestvovanie
protivorechilo by zakonu sohraneniya energii. Odnako mashiny, rabotayushchie bez
topliva, kotorye ya imeyu v vidu, sovershenno drugogo tipa i ih prinyato
nazyvat' vechnymi dvigatelyami vtorogo roda. Ih proektiruyut ne dlya togo, chtoby
poluchat' energiyu iz nichego, a dlya togo, chtoby izvlekat' ee iz teplovyh
rezervuarov, skrytyh vokrug nas v nedrah zemli, v more i v vozduhe.
Voobrazite sebe parohod, na kotorom par v kotlah poluchaetsya ne pri szhiganii
uglya, a pri izvlechenii tepla iz okruzhayushchej sudno vody. V samom dele, esli by
teplo mozhno bylo zastavit' tech' ot bolee holodnogo tela k bolee teplomu, a
ne v obratnom napravlenii, kak obychno, to mozhno bylo by postroit' sistemu,
kotoraya zakachivala by zabortnuyu morskuyu vodu, izvlekala by iz nee teplo i
stalkivala za bort poluchayushchiesya iz vody glyby l'da. Pri prevrashchenii v led
odnogo gallona vody, vydelyaetsya stol'ko tepla, chto ego dostatochno dlya togo,
chtoby dovesti do kipeniya drugoj gallon holodnoj vody. Propuskaya s pomoshch'yu
nasosov neskol'ko gallonov morskoj vody v minutu, mozhno legko poluchit'
kolichestvo teploty, dostatochnoe dlya raboty dvigatelya prilichnyh razmerov. Dlya
vseh prakticheskih celej vechnye dvigateli vtorogo roda nichem ne ustupali by
vechnym dvigatelyam pervogo roda, prednaznachennym dlya polucheniya energii iz
nichego. Esli by vechnye dvigateli vtorogo roda dejstvovali, to vse v mire
mogli by sushchestvovat' stol' zhe bezzabotno, kak chelovek, obladayushchij
besproigryshnoj strategiej dlya igry v ruletku. K sozhaleniyu, ni vechnye
dvigateli vtorogo roda, ni besproigryshnye strategii sushchestvovat' ne mogut,
ibo i te, i drugie odinakovo narushayut zakony veroyatnosti.
- YA mogu dopustit', chto pytat'sya izvlekat' teplo iz morskoj vody dlya
podogreva sudovyh kotlov - sumasshedshaya ideya, - skazal mister Tompkins. -
Odnako ya ne usmatrivayu nikakoj svyazi mezhdu etoj problemoj i zakonami sluchaya.
Razumeetsya, esli vy ne stanete predlagat' ispol'zovat' igral'nye kosti ili
koleso ruletki v kachestve dvizhushchihsya chastej mashin, rabotayushchih bez topliva.
No vy zhe nichego takogo, nadeyus', i ne predlagaete?
- Razumeetsya, ne predlagayu! - rassmeyalsya professor. - Ne dumayu takzhe,
chtoby samye sumasshedshie izobretateli vechnyh dvigatelej predlagali nechto
podobnoe. Delo sovsem v inom: teplovye processy sami ochen' pohozhi po svoej
prirode na igru v kosti, i nadeyat'sya na to, chto teplo potechet ot bolee
holodnogo tela k bolee goryachemu, vse ravno, chto nadeyat'sya na to, chto monety
iz banka kazino potekut k vam v karman.
- Vy hotite etim skazat', chto bank holodnyj, a moj karman goryachij? -
sprosil mister Tompkins, polnost'yu zaputavshijsya v ob座asneniyah.
- V kakom-to smysle da, - soglasilsya professor. - Esli by vy ne
propustili moyu lekciyu na proshloj nedele, to znali by, chto teplo predstavlyaet
soboj ne chto inoe, kak bystroe besporyadochnoe dvizhenie beschislennyh chastic,
izvestnyh pod nazvaniem atomov i molekul, iz kotoryh sostoyat vse
material'nye tela. CHem sil'nee eto molekulyarnoe dvizhenie, tem teplee telo.
Poskol'ku eto molekulyarnoe dvizhenie sovershenno besporyadochno, ono podchinyaetsya
zakonam sluchaya. Netrudno pokazat', chto naibolee veroyatnoe sostoyanie sistemy,
sostoyashchej iz bol'shogo chisla chastic, sootvetstvuet bolee ili menee
ravnomernomu raspredeleniyu vsej imeyushchejsya energii po chasticam. Esli kakaya-to
chast' material'nogo tela nagreta, t. e. esli chasticy v etoj chasti tela
dvizhutsya bystree, to, prinimaya vo vnimanie ogromnoe chislo sluchajnyh
stolknovenij, mozhno ozhidat', chto izbytok energii vskore ravnomerno
raspredelitsya mezhdu vsemi ostal'nymi chasticami. No poskol'ku stolknoveniya
mezhdu chasticami chisto sluchajnye, sushchestvuet takzhe veroyatnost' togo, chto
sovershenno sluchajno znachitel'naya chast' energii okazhetsya sosredotochennoj v
kakoj-to gruppe chastic v ushcherb vsem ostal'nym chasticam. Takaya spontannaya
koncentraciya teplovoj energii v kakoj-to odnoj chasti tela sootvetstvovala by
potoku tepla, napravlennomu protiv perepada, ili gradienta, temperatury, i v
principe otnyud' ne isklyuchaetsya. No esli my popytaemsya vychislit'
otnositel'nuyu veroyatnost' takoj spontannoj koncentracii tepla, to poluchim
stol' maloe chislovoe znachenie, chto podobnoe yavlenie s polnym osnovaniem
mozhno nazvat' prakticheski nevozmozhnym.
- Teper' mne ponyatno, - obradovalsya mister Tompkins. - Vy hotite
skazat', chto hotya vechnye dvigateli vtorogo roda mogut izredka rabotat',
veroyatnost' takogo sobytiya stol' zhe mala, kak veroyatnost' vypadeniya semi
ochkov sto raz podryad pri igre v kosti.
- V dejstvitel'nosti shansy vstretit' dejstvuyushchij vechnyj dvigatel'
vtorogo roda eshche men'she, - skazal professor. - Veroyatnosti vyigrysha v
azartnoj igre protiv prirody stol' maly, chto trudno najti podhodyashchie slova
dlya ih opisaniya. Naprimer, ya mogu podschitat' veroyatnost' togo, chto vozduh v
etoj komnate samoproizvol'no soberetsya pod stolom, ostaviv povsyudu
absolyutnyj vakuum. CHislo igral'nyh kostej, kotorye vy dolzhny byli by brosat'
odnovremenno, ekvivalentno chislu molekul vozduha v komnate, kotoroe mne bylo
by neobhodimo znat'. Naskol'ko ya pomnyu, odin kubicheskij santimetr vozduha
pri atmosfernom davlenii soderzhit dvadcatiznachnoe chislo molekul, poetomu vo
vsej komnate naberetsya dvadcatisemiznachnoe chislo molekul vozduha.
Prostranstvo pod stolom sostavlyaet primerno okolo odnogo procenta ob容ma
komnaty, i shansy lyuboj dannoj molekuly okazat'sya imenno pod stolom, a ne
gde-nibud' eshche, sostavlyayut poetomu odin k sta. Sledovatel'no, vychislyaya
veroyatnost' togo, chto vse molekuly okazhutsya pod stolom, ya dolzhen umnozhit'
odnu sotuyu na odnu sotuyu, na odnu sotuyu i t. d. stol'ko raz, skol'ko molekul
v komnate. V rezul'tate ya poluchu desyatichnuyu drob' s pyatidesyat'yu chetyr'mya
nulyami posle zapyatoj.
- Uf! - vzdohnul mister Tompkins. - Ne hotel by ya delat' stavku so
stol' malymi shansami na vyigrysh! A ne oznachaet li eto, chto otkloneniya ot
ravnoraspredeleniya molekul po prostranstvu poprostu nevozmozhny?
- Vy sovershenno pravy, - soglasilsya professor. - Mozhno schitat' tverdo
ustanovlennym faktom, chto smert' ot udush'ya iz-za togo, chto ves' vozduh
soberetsya pod stolom, nam ne ugrozhaet i zhidkost' v bokale ne zakipit vdrug
sama soboj. No esli my sosredotochim vnimanie na gorazdo men'shih oblastyah,
soderzhashchih sushchestvenno men'shee chislo nashih igral'nyh kostej - molekul, to
otkloneniya ot statisticheskogo raspredeleniya stanut znachitel'no bolee
veroyatnymi. Naprimer, v etoj zhe samoj komnate molekuly vozduha to i delo
gruppiruyutsya neskol'ko bolee plotno v odnih tochkah prostranstva, chem v
drugih, obrazuya slabye neodnorodnosti, kotorye poluchili nazvanie
statisticheskih fluktuacij plotnosti. Kogda solnechnyj svet prohodit cherez
zemnuyu atmosferu, takie neodnorodnosti privodyat k rasseyaniyu golubyh luchej
spektra i pridayut nebu znakomyj vsem goluboj cvet. Esli by ne bylo etih
fluktuacij plotnosti, to nebo vsegda bylo by sovershenno chernym i zvezdy byli
by otchetlivo vidny dazhe pri polnom dnevnom svete. Pri nagrevanii zhidkosti do
tochki kipeniya oni slegka mutneyut, chto takzhe ob座asnyaetsya temi zhe samymi
fluktuaciyami plotnosti, voznikayushchimi iz-za haotichnosti dvizheniya molekul. No
v bol'shih masshtabah fluktuacii nastol'ko maloveroyatny, chto my mogli by
naprasno prozhdat' ih milliardy let i tak i ne uvidet' ni odnoj fluktuacii.
- Tem ne menee u nas est' shans stat' svidetelyami kakogo-nibud'
neobychnogo sobytiya pryamo sejchas v etoj samoj komnate, - nastaival mister
Tompkins. - Ved' tak?
- Razumeetsya, takoj shans vsegda est', i bylo by nerazumno utverzhdat',
budto polovina soderzhimogo supnicy ne mozhet vyplesnut'sya na skatert' potomu,
chto polovina vseh molekul vnezapno priobrela teplovye skorosti v odnom i tom
zhe napravlenii.
- Imenno takoe sobytie proizoshlo lish' vchera, - vmeshalas' v razgovor
Mod, zakonchivshaya prosmatrivat' svoj zhurnal i s interesom slushavshaya besedu
professora i mistera Tompkinsa. - Sup prolilsya pryamo na skatert', hotya
gornichnaya utverzhdala, chto ne pritragivalas' k stolu.
Professor tiho rassmeyalsya.
- V etom konkretnom sluchae, - zametil on, - ya sklonen vinit' v
sluchivshemsya vse zhe gornichnuyu, a ne demona Maksvella.
- Demona Maksvella? - povtoril mister Tompkins v velichajshem izumlenii.
- A ya-to dumal, chto uchenye menee vsego pomyshlyayut o vsyakih tam demonah i
prochej chertovshchine.
- Po pravde govorya, my vosprinimaem ego ne slishkom ser'ezno, - poyasnil
professor. - Znamenityj fizik Dzhejms Klerk Maksvell vvel predstavlenie o
takom statisticheskom demone dlya bol'shej naglyadnosti. Demon ponadobilsya
Maksvellu pri rassmotrenii nekotoryh yavlenij, svyazannyh s teplotoj. Demon
Maksvella - sushchestvo ves'ma provornoe i uspevaet izmenyat' napravlenie
dvizheniya kazhdoj molekuly v otdel'nosti lyubym obrazom, kakim vy tol'ko
pozhelaete. Esli by takoj demon sushchestvoval v dejstvitel'nosti, to teplo
mozhno bylo by zastavit' tech' protiv gradienta temperatury i za
fundamental'nyj zakon termodinamiki, izvestnyj pod nazvaniem _principa
vozrastaniya entropii_, nikto by ne dal i lomanogo grosha.
- |ntropii? - peresprosil mister Tompkins. - Mne prihodilos' slyshat'
eto slovo i prezhde. Odin iz moih kolleg odnazhdy priglasil gostej, i posle
neskol'kih tostov prisutstvovavshie sredi priglashennyh studenty-himiki speli
na motiv "Ah, moj milyj Avgustin" kuplety, kotorye nachinalis' tak:
"Vozrastaet, ubyvaet,
Ubyvaet, vozrastaet -
Himiki togo ne znayut.
|ntropiya vozrastaet?"
Kstati, a chto takoe entropiya?
- Ponyat' eto sovsem netrudno. |ntropiya - eto prosto termin,
ispol'zuemyj dlya opisaniya stepeni besporyadochnosti dvizheniya molekul v lyubom
fizicheskom tele ili v sisteme tel. Mnogochislennye sluchajnye stolknoveniya
mezhdu molekulami vsegda sposobstvuyut uvelicheniyu entropii, tak kak polnyj
haos yavlyaetsya naibolee veroyatnym sostoyaniem lyubogo statisticheskogo ansamblya.
No esli by za rabotu prinyalsya demon Maksvella, to on dovol'no skoro smog by
navesti koe-kakoj poryadok v dvizhenii molekul tak zhe, kak horoshaya storozhevaya
sobaka ne daet razbezhat'sya i paset stado ovec, i togda entropiya sistemy
poshla by na ubyl'. Dolzhen skazat' vam takzhe, chto soglasno tak nazyvaemoj
N-teoreme, kotoroj my obyazany Lyudvigu Bol'cmanu...
YAvno zabyv o tom, chto on razgovarivaet s chelovekom, kotoryj prakticheski
nichego ne ponimaet v fizike, a ne chitaet lekciyu studentam-starshekursnikam,
professor s uvlecheniem prodolzhal svoj monolog i bez malejshih kolebanij
pribegal dazhe k takim malovrazumitel'nym dlya neposvyashchennyh terminam, kak
"obobshchennye parametry" i "kvaziergodicheskie sistemy". Emu kazalos', chto v
takom izlozhenii fundamental'nye zakony termodinamiki i ih svyaz' so
statisticheskoj mehanikoj Gibbsa stanovyatsya kristal'no yasnymi. Mister
Tompkins uzhe uspel privyknut' k tomu, chto ego test' iz座asnyaetsya na neskol'ko
nedostupnom dlya nego urovne, i poetomu s filosofskim spokojstviem potyagival
viski s sodovoj, pytayas' pridat' licu umnoe vyrazhenie. No ves' blesk i
krasota statisticheskoj fiziki yavno uskol'zali ot Mod, uyutno svernuvshejsya
kalachikom v svoem kresle i s geroicheskimi usiliyami borovshayasya s dremotoj.
Daby okonchatel'no razveyat' sonlivost', ona reshila vstat' i pojti posmotret',
kak idut prigotovleniya k obedu.
- Madam chto-nibud' zhelaet? - s poklonom sprosil ee vysokij tshchatel'no
odetyj dvoreckij, edva Mod poyavilas' na poroge stolovoj.
- Blagodaryu vas, nichego. Prosto reshila posmotret', kak idut
prigotovleniya k obedu, - otvetila ona, lihoradochno pytayas' ponyat', otkuda on
vzyalsya. Poyavlenie metrdotelya bylo ochen' strannym, poskol'ku prislugi
Tompkinsy ne derzhali, dvoreckogo u nih nikogda ne bylo, oni i podumat' ne
mogli o takoj roskoshi. Dvoreckij byl hudoshchav, stroen, so smugloj olivkovoj
kozhej, dlinnym kryuchkovatym nosom i zelenovatymi glazami, v kotoryh tlel
strannyj ogonek. Murashki probezhali u Mod po spine, kogda na lbu u dvoreckogo
ona zametila dva simmetrichnyh vystupa, tshchatel'no prikrytyh chernymi, kak
smol', volosami.
- Libo ya splyu, libo predo mnoj Mefistofel' sobstvennoj personoj pryamo s
opernyh podmostkov, - podumala ona.
- Vas nanyal moj muzh? - sprosila Mod lish' dlya togo, chtoby chto-nibud'
skazat'.
- Ne sovsem, - otvetil neobychnyj dvoreckij, zavershaya velikolepnuyu
servirovku stola. - Esli byt' tochnym, ya yavilsya syuda po sobstvennomu zhelaniyu,
daby pokazat' vashemu batyushke, izvestnomu svoimi poznaniyami, chto ya ne mif,
kak on dumaet. Pozvol'te predstavit'sya: ya demon Maksvella.
- O! - vymolvila Mod s oblegcheniem. - Togda vy, dolzhno byt', ne
zlokoznenny, kak drugie demony, i ne imeete namerenij prichinyat' vred
komu-nibud'.
- Razumeetsya, - uspokoil ee s shirokoj ulybkoj demon, - no ya lyublyu
razygryvat' s lyud'mi shutki i hochu podshutit' nad vashim uchenym batyushkoj.
- A chto vy namerevaetes' sdelat'? - s trevogoj sprosila Mod, kotoraya
nikak ne mogla otdelat'sya ot muchivshih ee podozrenij.
- Vzglyani sama, Mod, - predlozhil mister Tompkins, pokazyvaya svoej
supruge stat'yu, kotoruyu on izuchal s takim interesom v techenie poslednego
poluchasa. - YA nichego ne znayu o drugih vyigryshnyh strategiyah, no ta, o
kotoroj govoritsya v etoj stat'e, osnovana na ochen' prostyh matematicheskih
raschetah bez vsyakih obmanov i podvohov, i ya prosto ne znayu, gde zdes' v
rassuzhdeniya mozhet vkrast'sya kakaya-nibud' oshibka. CHtoby vyigrat', nuzhno lish'
vypisat' na listke bumagi chisla
i neukosnitel'no priderzhivat'sya prostyh pravil, privodimyh v toj zhe stat'e.
- Poprobovat', konechno, mozhno, - soglasilas' Mod, nachinaya proyavlyat'
priznaki interesa. - A chto eto za pravila?
- Dlya bol'shej naglyadnosti ya budu sledovat' primeru, privodimomu v
stat'e, ved', kak ty znaesh', uchit'sya luchshe vsego na primerah. V kachestve
illyustracii besproigryshnoj strategii avtor stat'i vybral igru v ruletku. Kak
tebe, dolzhno byt', izvestno, igroki v ruletku delayut stavku na krasnoe ili
na chernoe, t. e., po sushchestvu, kak by zaklyuchayut mezhdu soboj pari
otnositel'no ishoda brosaniya monety - vypadet li moneta vverh orlom ili
reshkoj. YA nachinayu s togo, chto vypisyvayu na listke bumagi chisla
Pervoe pravilo sostoit v tom, chto, delaya stavku, ya dolzhen vylozhit' na
stol chislo fishek, ravnoe summe pervogo i poslednego i vypisannyh chisel (a v
tom sluchae, esli na listke bumagi ostanetsya odno-edinstvennoe chislo, stavka
dolzhna byt' ravna odnomu chislu). Sleduya etomu pravilu, ya dolzhen vylozhit' na
stol chetyre (odnu plyus tri) fishki. Predpolozhim, chto ya stavlyu na krasnoe. Po
pravilam igry, v sluchae vyigrysha mne nuzhno zacherknut' pervoe i poslednee iz
vypisannyh chisel. V nashem primere eto chisla 1 i 3, poetomu, delaya sleduyushchuyu
stavku, ya dolzhen vylozhit' na stol dve fishki (poskol'ku posle vycherkivaniya
chisel 1 i 3 na listke bumagi ostanetsya odno-edinstvennoe chislo 2). V sluchae
proigrysha chislo fishek v predydushchej (proigrannoj) stavke neobhodimo pripisat'
sprava k uzhe vypisannym chislam, a pri opredelenii velichiny sleduyushchej stavki
priderzhivat'sya prezhnego pravila, t. e. vystavit' chislo fishek, ravnoe summe
pervogo i poslednego iz vypisannyh chisel (libo, esli na listke bumagi
ostanetsya tol'ko odno chislo, to etomu chislu).
Predpolozhim, chto ruletka ostanovitsya na chernom i krup'e special'noj
lopatkoj podvinet k sebe vystavlennye mnoj chetyre fishki. Poskol'ku ya
proigral, novyj ryad chisel, vypisannyh na listke bumagi, vyglyadit teper' tak:
(chislo vylozhennyh na stol fishek, ravnoe 4, pripisano sprava). Delaya
sleduyushchuyu stavku, ya dolzhen vylozhit' na stol pyat' (odnu plyus chetyre) fishek. V
stat'e govoritsya, chto i vo vtoroj raz ya snova proigryvayu i chto, nesmotrya na
povtornyj proigrysh, mne nadlezhit priderzhivat'sya prezhnej strategii, t. e.
pripisat' k uzhe vypisannym chislam sprava chislo 5 i vylozhit' na stol shest'
(odnu plyus pyat') fishek.
- Na etot raz ty nepremenno dolzhen vyigrat', - voskliknula Mod, vse
bolee vhodya v azart. - Ne mozhesh' zhe ty vse vremya proigryvat'!
- Eshche kak mogu! - zaveril suprugu mister Tompkins. - V detstve ya
chasten'ko igral s drugimi mal'chishkami v orlyanku - zaklyuchal pari otnositel'no
togo, kakoj storonoj vverh vypadet broshennaya moneta i, hochesh' ver', hochesh'
ne ver', odnazhdy stal svidetelem togo, kak moneta desyat' raz podryad vypala
vverh orlom. No predpolozhim, kak eto delaetsya v stat'e, chto na etot raz ya
dlya raznoobraziya vyigral. V etom sluchae po pravilam igry ya dolzhen poluchit'
svoyu udvoennuyu stavku - dvenadcat' fishek - i po sravneniyu so svoim
pervonachal'nym kapitalom stanu na tri fishki bogache. Sleduya rekomenduemoj
strategii, ya dolzhen vycherknut' chisla 1 i 5, posle chego zapis' na listke
bumagi primet sleduyushchij vid:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto)
Delaya sleduyushchuyu stavku, ya dolzhen vylozhit' na stol shest' (dve plyus
chetyre) fishek.
- Zdes' v stat'e napisano, chto ty snova proigral, - vzdohnula Mod,
zaglyadyvaya v zhurnal cherez plecho muzha. - Znachit, teper' ty dolzhen pripisat' k
chislam sprava shesterku i, delaya sleduyushchuyu stavku, vylozhit' na stol vosem'
fishek. Pravil'no?
- Ty absolyutno prava, no i na etot raz menya podsteregaet proigrysh, i
zapis' na listke bumagi vyglyadit teper' tak:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto), 6, 8
Delaya ocherednuyu stavku, ya dolzhen teper' vylozhit' na stol desyat' (dve
plyus vosem') fishek. V stat'e govoritsya, chto na etot raz ya vyigral. Znachit, ya
dolzhen zacherknut' chisla 2 i 8 i, delaya sleduyushchuyu stavku, vylozhit' na stol
devyat' (tri plyus shest') fishek. No tut menya (tak govoritsya v stat'e) snova
podsteregaet proigrysh.
- Kakoj vse-taki neudachnyj primer! - posetovala, naduv gubki, Mod. - Ty
uspel proigrat' tri raza, a vyigral vsego lish' odin raz!
- Nevazhno, - uspokoil ee mister Tompkins so snishoditel'noj
uverennost'yu fokusnika. - Vse ravno v samom konce cikla vyigrysh ostanetsya za
nami. Poslednij zapusk ruletki prines mne (po utverzhdeniyu avtora stat'i)
proigrysh v devyat' fishek. Poetomu teper' ya dolzhen pripisat' k uzhe vypisannym
chislam sprava devyatku, posle chego zapis' na moem listke budet vyglyadet' tak:
1 (zacherknuto), 2 (zacherknuto), 3, 4, 5 (zacherknuto), 6, 8 (zacherknuto), 9
Na stol mne nuzhno vylozhit' dvenadcat' (tri plyus devyat') fishek. Na etot
raz vyigrysh ostaetsya za mnoj, poetomu ya vycherkivayu chisla 3 i 9 i, delaya
novuyu stavku, vykladyvayu na stol desyat' (chetyre plyus shest') fishek.
Posleduyushchij vyigrysh zavershaet cikl, tak kak vse chisla, vypisannye na listke
bumagi, okazyvayutsya zacherknutymi. YA stal bogache na shest' fishek, hotya vyigral
v ruletku tol'ko chetyre raza, a proigral pyat' raz!
- A ty dejstvitel'no stal na shest' fishek bogache? - nedoverchivo sprosila
Mod.
- V etom ne mozhet byt' nikakih somnenij. Strategiya postroena tak, chto
vsyakij raz po zavershenii cikla ty, hochesh', ne hochesh', nepremenno vyigryvaesh'
shest' fishek. V etom netrudno ubedit'sya s pomoshch'yu neslozhnyh vychislenij,
poetomu ya nazyvayu etu strategiyu matematicheskoj. Kak vidish', ona
besproigryshna. Esli ugodno, mozhesh' vzyat' listok bumagi i proverit' vse
vykladki sama.
- Veryu tebe na slovo, chto strategiya dejstvitel'no besproigryshna, -
zadumchivo skazala Mod, - no ved' shest' fishchek - ne takoj uzh bol'shoj vyigrysh.
- Kak skazat', - vozrazil mister Tompkins, - ved' vyigrysh shesti fishek v
konce kazhdogo cikla _garantirovan_. Povtoryaya proceduru snova i snova
(nachinaya kazhdyj raz s vypisyvaniya chisel 1, 2, 3), ty mozhesh' vyigrat' skol'ko
tvoej dushe ugodno deneg, a eto sovsem neploho.
- |to prosto velikolepno! - soglasilas' Mod. - Teper' ty smozhesh'
ostavit' sluzhbu v banke, my smozhem pereehat' v bolee prostornuyu kvartiru, a
ne dalee, kak vchera, ya videla v vitrine odnogo mehovogo magazina chudesnoe
manto. I stoit ono kakih-nibud'...
- Razumeetsya, my kupim tebe eto manto, dorogaya, - pospeshil zaverit'
zhenu mister Tompkins. - No snachala nam nuzhno kak mozhno skoree otpravit'sya v
Monte-Karlo. Ved' stat'yu, opublikovannuyu v zhurnale "Esquire", prochitaet
mnozhestvo lyudej, i bylo by ochen' dosadno pribyt' v Monte-Karlo lish' dlya
togo, chtoby zastat' tam schastlivchika, kotoryj operedil nas i dovel kazino do
polnogo razoreniya.
- YA sejchas pozvonyu v aeroport, - predlozhila Mod, - i uznayu, kogda
otpravlyaetsya blizhajshij rejs v Monte-Karlo.
- CHto za speshka? - razdalsya v prihozhej znakomyj golos, i v komnatu
voshel staryj professor. Ostanovivshis' v dveryah, on s udivleniem smotrel na
supruzheskuyu chetu Tompkinsov, neskol'ko razgoryachennyh vnezapno otkryvshimisya
pered nimi perspektivami finansovogo blagopoluchiya.
- My namerevaemsya otpravit'sya blizhajshim zhe rejsom v Monte-Karlo i
nadeemsya vernut'sya osnovatel'no razbogatevshimi, - poyasnil mister Tompkins,
podnimayas' iz kresla navstrechu testyu.
- Ah, vot v chem delo! Togda vse ponyatno, - ulybnulsya professor, s
komfortom ustraivayas' v staromodnom kresle u kamina. - U vas est' novaya
besproigryshnaya strategiya?
- No, papa, eta strategiya dejstvitel'no besproigryshnaya, - s uprekom
skazala Mod, vse eshche derzha ruku na telefonnoj trubke.
- Mod sovershenno prava, - podtverdil mister Tompkins, protyagivaya
professoru zhurnal. - Predlagaemaya strategiya prosto ne mozhet ne vyigrat'!
- Tak-taki i ne mozhet? - ironicheski peresprosil professor s ulybkoj. -
Sejchas uvidim!
Beglo oznakomivshis' so stat'ej, professor prodolzhal:
- Otlichitel'naya osobennost' predlagaemoj strategii sostoit v tom, chto
pravilo, reguliruyushchee velichinu stavok, zastavlyaet vas uvelichivat' stavku
posle kazhdogo proigrysha i snizhat' stavku posle kazhdogo vyigrysha.
Sledovatel'no, esli vy budete poperemenno vyigryvat' i proigryvat', prichem
vyigryshi i proigryshi budut cheredovat'sya s absolyutnoj regulyarnost'yu, to vash
kapital budet kolebat'sya, prichem kazhdoe uvelichenie kapitala budet chut'
bol'she ego umen'sheniya. V etom sluchae vy, nesomnenno, dostatochno skoro
stanete millionerom. No, kak vy ponimaete, absolyutnaya regulyarnost'
vstrechaetsya nechasto. V dejstvitel'nosti veroyatnost' poyavleniya pravil'no
chereduyushchejsya posledovatel'nosti vyigryshej i proigryshej stol' zhe mala, kak i
veroyatnost' poyavleniya odinakovoj po dline serii odnih tol'ko vyigryshej.
Takim obrazom, neobhodimo vyyasnit', chto proizojdet, esli neskol'ko vyigryshej
(ili neskol'ko proigryshej) sleduyut podryad drug za drugom. Esli vam, kak
govoryat igroki, ulybnulas' fortuna, to pravila besproigryshnoj strategii
vynuzhdayut vas libo ponizhat', libo po krajnej mere ne povyshat' stavku posle
kazhdogo vyigrysha, poetomu obshchij vyigrysh okazhetsya ne slishkom bol'shim. S
drugoj storony, te zhe pravila zastavlyayut vas posle kazhdogo proigrysha
povyshat' stavku, poetomu polosa neudach mozhet imet' dlya vas katastroficheskie
posledstviya i dazhe pobudit' vas vyjti iz igry. Krivaya kolebanij vashego
kapitala na etot raz sostoit iz neskol'kih medlenno vozrastayushchih uchastkov,
smenyayushchihsya rezkimi spadami. V nachale igry vy s bol'shej veroyatnost'yu
popadaete na dlinnuyu medlenno vozrastayushchuyu chast' krivoj i v techenie
kakogo-to vremeni naslazhdaetes' priyatnym oshchushcheniem togo, chto vash kapital
medlenno, no neuklonno uvelichivaetsya. No esli vy prodolzhaete igru dostatochno
dolgo v nadezhde na poluchenie vse bol'shej i bol'shej pribyli, to sovershenno
neozhidanno dlya vas vnezapno nastupaet rezkij spad, kotoryj mozhet okazat'sya
dostatochno glubokim dlya togo, chtoby vy, sdelav ocherednuyu stavku, poteryali
poslednij penni. Mozhno pokazat', prichem v sovershenno obshchem vide, chto v
predlagaemoj avtorom stat'i strategii, ravno kak i v lyuboj drugoj vyigryshnoj
strategii, veroyatnost' togo, chto krivaya dostignet dvojnoj otmetki, ravna
veroyatnosti dostignut' nulevogo znacheniya. Inache govorya, vy imeete tochno
takoj zhe shans na okonchatel'nyj vyigrysh, kak esli by postavili vse svoi
den'gi na krasnoe ili chernoe i udvoili svoj kapital ili spustili vse, chto
imeli, za odin-edinstvennyj zapusk ruletki. Vse "besproigryshnye" strategii
sposobny lish' prodlit' igru i tem samym dat' vam vozmozhnost' poluchit' za
svoi den'gi bol'she udovol'stviya. No dazhe esli vy ne trebuete ot igry nichego
bol'shego, to i togda igru ne sleduet tak uslozhnyat'. Kak vy znaete, na obode
kolesa ruletki naneseny tridcat' shest' chisel. Nichto ne meshaet postavit' po
fishke na kazhdoe iz chisel, krome kakogo-nibud' odnogo. V etom sluchae vy
imeete tridcat' pyat' shansov iz tridcati shesti na vyigrysh i na to, chto bank
vyplatit vam za odnu fishku bol'she, chem te tridcat' pyat' fishek, kotorye vy,
delaya stavku, vylozhili na stol. Odnako v odnom iz tridcati shesti zapuskov
ruletochnogo kolesa sharik ostanovitsya na tom chisle, na kotoroe vy reshili ne
stavit' svoyu fishku, i vy poteryaete vse svoi tridcat' pyat' fishek. Esli vy
budete priderzhivat'sya takoj strategii v dostatochno prodolzhitel'noj igre, to
krivaya vashego fluktuiruyushchego kapitala budet vyglyadet' tochno tak zhe, kak
krivaya, kotoruyu vy poluchili, sleduya strategii, predlozhennoj zhurnalom.
Razumeetsya, v svoih rassuzhdeniyah ya ishodil iz predpolozheniya o tom, chto
bank ne predprinimaet nikakih mer, chtoby iskusstvenno ponizit' shansy igroka
na vyigrysh. V dejstvitel'nosti zhe na kazhdom ruletochnom kolese, kotoroe mne
prihodilos' videt', byl nul' - "zero", a inogda dazhe dva nulya, chto ponizhaet
shansy igroka na vyigrysh. Takim obrazom, nezavisimo ot vybrannoj igrokom
strategii ego denezhki malo-pomalu perekochevyvayut iz ego karmana v karman
vladel'ca kazino.
- Vy hotite skazat', - udruchenno progovoril mister Tompkins, - chto
nadezhnoj besproigryshnoj strategii ne sushchestvuet i chto vyigrat' den'gi bez
riska proigrat' s veroyatnost'yu chut' bol'she, chem veroyatnost' vyigrysha, prosto
nevozmozhno?
- Imenno eto ya hotel skazat'! - podtverdil dogadku mistera Tompkinsa
professor. - Bolee togo, vyskazannye mnoj soobrazheniya otnosyatsya ne tol'ko k
takim v sushchnosti pustyakovym problemam, kak azartnye igry, no i ko mnogim
razlichnym fizicheskim yavleniyam, kotorye, na pervyj vzglyad, ne imeyut nikakogo
otnosheniya k veroyatnostnym zakonam. Poetomu esli by vam udalos' izobresti
nadezhnuyu vyigryshnuyu strategiyu dlya preodoleniya zakonov sluchaya, to dlya nee
nashlos' by nemalo gorazdo bolee uvlekatel'nyh primenenij, chem igra na den'gi
v kazino. Naprimer, takaya strategiya pozvolila by sozdavat' avtomashiny,
sposobnye sovershat' probegi lyuboj protyazhennosti bez kapli benzina, stroit'
fabriki, rabotayushchie bez uglya, i osushchestvlyat' mnozhestvo drugih ne menee
fantasticheskih proektov.
- YA gde-to chital o takih fantasticheskih mashinah. Kazhetsya, oni
nazyvayutsya vechnymi dvigatelyami? - zametil mister Tompkins. - Esli ya
pravil'no pomnyu, vechnye dvigateli po zamyslu ih sozdatelej dolzhny byli by
rabotat' bez topliva. Prinyato schitat', chto oni nevozmozhny potomu, chto
energiyu nevozmozhno proizvodit' iz nichego. No kak by to ni bylo, vechnye
dvigateli ne imeyut nikakogo otnosheniya k azartnym igram.
- Vy sovershenno pravy, molodoj chelovek, - soglasilsya professor,
neskazanno dovol'nyj tem, chto ego zyat' nachinaet ponemnogu razbirat'sya v
fizike. - Takie vechnye dvigateli (ih prinyato nazyvat' vechnymi dvigatelyami
pervogo roda) ne mogut sushchestvovat' potomu, chto ih sushchestvovanie
protivorechilo by zakonu sohraneniya energii. Odnako mashiny, rabotayushchie bez
topliva, kotorye ya imeyu v vidu, sovershenno drugogo tipa i ih prinyato
nazyvat' vechnymi dvigatelyami vtorogo roda. Ih proektiruyut ne dlya togo, chtoby
poluchat' energiyu iz nichego, a dlya togo, chtoby izvlekat' ee iz teplovyh
rezervuarov, skrytyh vokrug nas v nedrah zemli, v more i v vozduhe.
Voobrazite sebe parohod, na kotorom par v kotlah poluchaetsya ne pri szhiganii
uglya, a pri izvlechenii tepla iz okruzhayushchej sudno vody. V samom dele, esli by
teplo mozhno bylo zastavit' tech' ot bolee holodnogo tela k bolee teplomu, a
ne v obratnom napravlenii, kak obychno, to mozhno bylo by postroit' sistemu,
kotoraya zakachivala by zabortnuyu morskuyu vodu, izvlekala by iz nee teplo i
stalkivala za bort poluchayushchiesya iz vody glyby l'da. Pri prevrashchenii v led
odnogo gallona vody, vydelyaetsya stol'ko tepla, chto ego dostatochno dlya togo,
chtoby dovesti do kipeniya drugoj gallon holodnoj vody. Propuskaya s pomoshch'yu
nasosov neskol'ko gallonov morskoj vody v minutu, mozhno legko poluchit'
kolichestvo teploty, dostatochnoe dlya raboty dvigatelya prilichnyh razmerov. Dlya
vseh prakticheskih celej vechnye dvigateli vtorogo roda nichem ne ustupali by
vechnym dvigatelyam pervogo roda, prednaznachennym dlya polucheniya energii iz
nichego. Esli by vechnye dvigateli vtorogo roda dejstvovali, to vse v mire
mogli by sushchestvovat' stol' zhe bezzabotno, kak chelovek, obladayushchij
besproigryshnoj strategiej dlya igry v ruletku. K sozhaleniyu, ni vechnye
dvigateli vtorogo roda, ni besproigryshnye strategii sushchestvovat' ne mogut,
ibo i te, i drugie odinakovo narushayut zakony veroyatnosti.
- YA mogu dopustit', chto pytat'sya izvlekat' teplo iz morskoj vody dlya
podogreva sudovyh kotlov - sumasshedshaya ideya, - skazal mister Tompkins. -
Odnako ya ne usmatrivayu nikakoj svyazi mezhdu etoj problemoj i zakonami sluchaya.
Razumeetsya, esli vy ne stanete predlagat' ispol'zovat' igral'nye kosti ili
koleso ruletki v kachestve dvizhushchihsya chastej mashin, rabotayushchih bez topliva.
No vy zhe nichego takogo, nadeyus', i ne predlagaete?
- Razumeetsya, ne predlagayu! - rassmeyalsya professor. - Ne dumayu takzhe,
chtoby samye sumasshedshie izobretateli vechnyh dvigatelej predlagali nechto
podobnoe. Delo sovsem v inom: teplovye processy sami ochen' pohozhi po svoej
prirode na igru v kosti, i nadeyat'sya na to, chto teplo potechet ot bolee
holodnogo tela k bolee goryachemu, vse ravno, chto nadeyat'sya na to, chto monety
iz banka kazino potekut k vam v karman.
- Vy hotite etim skazat', chto bank holodnyj, a moj karman goryachij? -
sprosil mister Tompkins, polnost'yu zaputavshijsya v ob座asneniyah.
- V kakom-to smysle da, - soglasilsya professor. - Esli by vy ne
propustili moyu lekciyu na proshloj nedele, to znali by, chto teplo predstavlyaet
soboj ne chto inoe, kak bystroe besporyadochnoe dvizhenie beschislennyh chastic,
izvestnyh pod nazvaniem atomov i molekul, iz kotoryh sostoyat vse
material'nye tela. CHem sil'nee eto molekulyarnoe dvizhenie, tem teplee telo.
Poskol'ku eto molekulyarnoe dvizhenie sovershenno besporyadochno, ono podchinyaetsya
zakonam sluchaya. Netrudno pokazat', chto naibolee veroyatnoe sostoyanie sistemy,
sostoyashchej iz bol'shogo chisla chastic, sootvetstvuet bolee ili menee
ravnomernomu raspredeleniyu vsej imeyushchejsya energii po chasticam. Esli kakaya-to
chast' material'nogo tela nagreta, t. e. esli chasticy v etoj chasti tela
dvizhutsya bystree, to, prinimaya vo vnimanie ogromnoe chislo sluchajnyh
stolknovenij, mozhno ozhidat', chto izbytok energii vskore ravnomerno
raspredelitsya mezhdu vsemi ostal'nymi chasticami. No poskol'ku stolknoveniya
mezhdu chasticami chisto sluchajnye, sushchestvuet takzhe veroyatnost' togo, chto
sovershenno sluchajno znachitel'naya chast' energii okazhetsya sosredotochennoj v
kakoj-to gruppe chastic v ushcherb vsem ostal'nym chasticam. Takaya spontannaya
koncentraciya teplovoj energii v kakoj-to odnoj chasti tela sootvetstvovala by
potoku tepla, napravlennomu protiv perepada, ili gradienta, temperatury, i v
principe otnyud' ne isklyuchaetsya. No esli my popytaemsya vychislit'
otnositel'nuyu veroyatnost' takoj spontannoj koncentracii tepla, to poluchim
stol' maloe chislovoe znachenie, chto podobnoe yavlenie s polnym osnovaniem
mozhno nazvat' prakticheski nevozmozhnym.
- Teper' mne ponyatno, - obradovalsya mister Tompkins. - Vy hotite
skazat', chto hotya vechnye dvigateli vtorogo roda mogut izredka rabotat',
veroyatnost' takogo sobytiya stol' zhe mala, kak veroyatnost' vypadeniya semi
ochkov sto raz podryad pri igre v kosti.
- V dejstvitel'nosti shansy vstretit' dejstvuyushchij vechnyj dvigatel'
vtorogo roda eshche men'she, - skazal professor. - Veroyatnosti vyigrysha v
azartnoj igre protiv prirody stol' maly, chto trudno najti podhodyashchie slova
dlya ih opisaniya. Naprimer, ya mogu podschitat' veroyatnost' togo, chto vozduh v
etoj komnate samoproizvol'no soberetsya pod stolom, ostaviv povsyudu
absolyutnyj vakuum. CHislo igral'nyh kostej, kotorye vy dolzhny byli by brosat'
odnovremenno, ekvivalentno chislu molekul vozduha v komnate, kotoroe mne bylo
by neobhodimo znat'. Naskol'ko ya pomnyu, odin kubicheskij santimetr vozduha
pri atmosfernom davlenii soderzhit dvadcatiznachnoe chislo molekul, poetomu vo
vsej komnate naberetsya dvadcatisemiznachnoe chislo molekul vozduha.
Prostranstvo pod stolom sostavlyaet primerno okolo odnogo procenta ob容ma
komnaty, i shansy lyuboj dannoj molekuly okazat'sya imenno pod stolom, a ne
gde-nibud' eshche, sostavlyayut poetomu odin k sta. Sledovatel'no, vychislyaya
veroyatnost' togo, chto vse molekuly okazhutsya pod stolom, ya dolzhen umnozhit'
odnu sotuyu na odnu sotuyu, na odnu sotuyu i t. d. stol'ko raz, skol'ko molekul
v komnate. V rezul'tate ya poluchu desyatichnuyu drob' s pyatidesyat'yu chetyr'mya
nulyami posle zapyatoj.
- Uf! - vzdohnul mister Tompkins. - Ne hotel by ya delat' stavku so
stol' malymi shansami na vyigrysh! A ne oznachaet li eto, chto otkloneniya ot
ravnoraspredeleniya molekul po prostranstvu poprostu nevozmozhny?
- Vy sovershenno pravy, - soglasilsya professor. - Mozhno schitat' tverdo
ustanovlennym faktom, chto smert' ot udush'ya iz-za togo, chto ves' vozduh
soberetsya pod stolom, nam ne ugrozhaet i zhidkost' v bokale ne zakipit vdrug
sama soboj. No esli my sosredotochim vnimanie na gorazdo men'shih oblastyah,
soderzhashchih sushchestvenno men'shee chislo nashih igral'nyh kostej - molekul, to
otkloneniya ot statisticheskogo raspredeleniya stanut znachitel'no bolee
veroyatnymi. Naprimer, v etoj zhe samoj komnate molekuly vozduha to i delo
gruppiruyutsya neskol'ko bolee plotno v odnih tochkah prostranstva, chem v
drugih, obrazuya slabye neodnorodnosti, kotorye poluchili nazvanie
statisticheskih fluktuacij plotnosti. Kogda solnechnyj svet prohodit cherez
zemnuyu atmosferu, takie neodnorodnosti privodyat k rasseyaniyu golubyh luchej
spektra i pridayut nebu znakomyj vsem goluboj cvet. Esli by ne bylo etih
fluktuacij plotnosti, to nebo vsegda bylo by sovershenno chernym i zvezdy byli
by otchetlivo vidny dazhe pri polnom dnevnom svete. Pri nagrevanii zhidkosti do
tochki kipeniya oni slegka mutneyut, chto takzhe ob座asnyaetsya temi zhe samymi
fluktuaciyami plotnosti, voznikayushchimi iz-za haotichnosti dvizheniya molekul. No
v bol'shih masshtabah fluktuacii nastol'ko maloveroyatny, chto my mogli by
naprasno prozhdat' ih milliardy let i tak i ne uvidet' ni odnoj fluktuacii.
- Tem ne menee u nas est' shans stat' svidetelyami kakogo-nibud'
neobychnogo sobytiya pryamo sejchas v etoj samoj komnate, - nastaival mister
Tompkins. - Ved' tak?
- Razumeetsya, takoj shans vsegda est', i bylo by nerazumno utverzhdat',
budto polovina soderzhimogo supnicy ne mozhet vyplesnut'sya na skatert' potomu,
chto polovina vseh molekul vnezapno priobrela teplovye skorosti v odnom i tom
zhe napravlenii.
- Imenno takoe sobytie proizoshlo lish' vchera, - vmeshalas' v razgovor
Mod, zakonchivshaya prosmatrivat' svoj zhurnal i s interesom slushavshaya besedu
professora i mistera Tompkinsa. - Sup prolilsya pryamo na skatert', hotya
gornichnaya utverzhdala, chto ne pritragivalas' k stolu.
Professor tiho rassmeyalsya.
- V etom konkretnom sluchae, - zametil on, - ya sklonen vinit' v
sluchivshemsya vse zhe gornichnuyu, a ne demona Maksvella.
- Demona Maksvella? - povtoril mister Tompkins v velichajshem izumlenii.
- A ya-to dumal, chto uchenye menee vsego pomyshlyayut o vsyakih tam demonah i
prochej chertovshchine.
- Po pravde govorya, my vosprinimaem ego ne slishkom ser'ezno, - poyasnil
professor. - Znamenityj fizik Dzhejms Klerk Maksvell vvel predstavlenie o
takom statisticheskom demone dlya bol'shej naglyadnosti. Demon ponadobilsya
Maksvellu pri rassmotrenii nekotoryh yavlenij, svyazannyh s teplotoj. Demon
Maksvella - sushchestvo ves'ma provornoe i uspevaet izmenyat' napravlenie
dvizheniya kazhdoj molekuly v otdel'nosti lyubym obrazom, kakim vy tol'ko
pozhelaete. Esli by takoj demon sushchestvoval v dejstvitel'nosti, to teplo
mozhno bylo by zastavit' tech' protiv gradienta temperatury i za
fundamental'nyj zakon termodinamiki, izvestnyj pod nazvaniem _principa
vozrastaniya entropii_, nikto by ne dal i lomanogo grosha.
- |ntropii? - peresprosil mister Tompkins. - Mne prihodilos' slyshat'
eto slovo i prezhde. Odin iz moih kolleg odnazhdy priglasil gostej, i posle
neskol'kih tostov prisutstvovavshie sredi priglashennyh studenty-himiki speli
na motiv "Ah, moj milyj Avgustin" kuplety, kotorye nachinalis' tak:
"Vozrastaet, ubyvaet,
Ubyvaet, vozrastaet -
Himiki togo ne znayut.
|ntropiya vozrastaet?"
Kstati, a chto takoe entropiya?
- Ponyat' eto sovsem netrudno. |ntropiya - eto prosto termin,
ispol'zuemyj dlya opisaniya stepeni besporyadochnosti dvizheniya molekul v lyubom
fizicheskom tele ili v sisteme tel. Mnogochislennye sluchajnye stolknoveniya
mezhdu molekulami vsegda sposobstvuyut uvelicheniyu entropii, tak kak polnyj
haos yavlyaetsya naibolee veroyatnym sostoyaniem lyubogo statisticheskogo ansamblya.
No esli by za rabotu prinyalsya demon Maksvella, to on dovol'no skoro smog by
navesti koe-kakoj poryadok v dvizhenii molekul tak zhe, kak horoshaya storozhevaya
sobaka ne daet razbezhat'sya i paset stado ovec, i togda entropiya sistemy
poshla by na ubyl'. Dolzhen skazat' vam takzhe, chto soglasno tak nazyvaemoj
N-teoreme, kotoroj my obyazany Lyudvigu Bol'cmanu...
YAvno zabyv o tom, chto on razgovarivaet s chelovekom, kotoryj prakticheski
nichego ne ponimaet v fizike, a ne chitaet lekciyu studentam-starshekursnikam,
professor s uvlecheniem prodolzhal svoj monolog i bez malejshih kolebanij
pribegal dazhe k takim malovrazumitel'nym dlya neposvyashchennyh terminam, kak
"obobshchennye parametry" i "kvaziergodicheskie sistemy". Emu kazalos', chto v
takom izlozhenii fundamental'nye zakony termodinamiki i ih svyaz' so
statisticheskoj mehanikoj Gibbsa stanovyatsya kristal'no yasnymi. Mister
Tompkins uzhe uspel privyknut' k tomu, chto ego test' iz座asnyaetsya na neskol'ko
nedostupnom dlya nego urovne, i poetomu s filosofskim spokojstviem potyagival
viski s sodovoj, pytayas' pridat' licu umnoe vyrazhenie. No ves' blesk i
krasota statisticheskoj fiziki yavno uskol'zali ot Mod, uyutno svernuvshejsya
kalachikom v svoem kresle i s geroicheskimi usiliyami borovshayasya s dremotoj.
Daby okonchatel'no razveyat' sonlivost', ona reshila vstat' i pojti posmotret',
kak idut prigotovleniya k obedu.
- Madam chto-nibud' zhelaet? - s poklonom sprosil ee vysokij tshchatel'no
odetyj dvoreckij, edva Mod poyavilas' na poroge stolovoj.
- Blagodaryu vas, nichego. Prosto reshila posmotret', kak idut
prigotovleniya k obedu, - otvetila ona, lihoradochno pytayas' ponyat', otkuda on
vzyalsya. Poyavlenie metrdotelya bylo ochen' strannym, poskol'ku prislugi
Tompkinsy ne derzhali, dvoreckogo u nih nikogda ne bylo, oni i podumat' ne
mogli o takoj roskoshi. Dvoreckij byl hudoshchav, stroen, so smugloj olivkovoj
kozhej, dlinnym kryuchkovatym nosom i zelenovatymi glazami, v kotoryh tlel
strannyj ogonek. Murashki probezhali u Mod po spine, kogda na lbu u dvoreckogo
ona zametila dva simmetrichnyh vystupa, tshchatel'no prikrytyh chernymi, kak
smol', volosami.
- Libo ya splyu, libo predo mnoj Mefistofel' sobstvennoj personoj pryamo s
opernyh podmostkov, - podumala ona.
- Vas nanyal moj muzh? - sprosila Mod lish' dlya togo, chtoby chto-nibud'
skazat'.
- Ne sovsem, - otvetil neobychnyj dvoreckij, zavershaya velikolepnuyu
servirovku stola. - Esli byt' tochnym, ya yavilsya syuda po sobstvennomu zhelaniyu,
daby pokazat' vashemu batyushke, izvestnomu svoimi poznaniyami, chto ya ne mif,
kak on dumaet. Pozvol'te predstavit'sya: ya demon Maksvella.
- O! - vymolvila Mod s oblegcheniem. - Togda vy, dolzhno byt', ne
zlokoznenny, kak drugie demony, i ne imeete namerenij prichinyat' vred
komu-nibud'.
- Razumeetsya, - uspokoil ee s shirokoj ulybkoj demon, - no ya lyublyu
razygryvat' s lyud'mi shutki i hochu podshutit' nad vashim uchenym batyushkoj.
- A chto vy namerevaetes' sdelat'? - s trevogoj sprosila Mod, kotoraya
nikak ne mogla otdelat'sya ot muchivshih ee podozrenij.
 - Prosto prodemonstrirovat' emu, chto esli ya zahochu, to mogu narushit'
princip vozrastaniya entropii. A chtoby i vy mogli ubedit'sya v etom, ya byl by
ochen' priznatelen vam, esli by vy sostavili mne kompaniyu. Smeyu uverit' vas,
chto vam ne ugrozhaet nikakaya opasnost'.
Pri etih slovah Mod pochuvstvovala, kak demon krepko vzyal ee pod ruku i
vse predmety vokrug slovno soshli s uma. Stol, stul'ya i vsya prochaya obstanovka
stolovoj vdrug nachali s chudovishchnoj skorost'yu uvelichivat'sya, i na ee glazah
spinka kresla, vyrosshaya do gigantskih razmerov, zakryla gorizont. Kogda vse
vokrug postepenno uspokoilos', Mod obnaruzhila, chto plavaet v vozduhe,
podderzhivaemaya svoim neobychnym sputnikom. Kakie-to tumannye shary razmerom s
tennisnyj myach so svistom pronosilis' mimo po vsem napravleniyam. Demon
Maksvella predusmotritel'no predotvrashchal ih ot stolknoveniya so vsemi
malo-mal'ski opasnymi predmetami. Vzglyanuv vniz, Mod uvidela nechto vrode
rybackoj lodki, do samyh uklyuchin gruzhenoj trepyhayushchejsya, bleshchushchej serebrom
ryboj. Prismotrevshis' povnimatel'nee, Mod uvidela, chto eto byli ne ryby, a
mnozhestvo tumannyh sharov, vrode teh, chto to i delo proletali mimo, so
svistom rassekaya vozduh. Demon, po-prezhnemu krepko derzha ee pod ruku, vlek
ee za soboj do teh por, poka oni ne ochutilis' v more kakoj-to zernistoj
zhidkosti, besformennoj i v to zhe vremya podvizhnoj. SHary pryamo-taki kipeli u
samoj poverhnosti morya, a nekotoryh zhidkost' zasasyvala, i oni skryvalis' v
puchine. Vremya ot vremeni nekotorye shary vsplyvali k samoj poverhnosti s
takoj skorost'yu, chto otryvalis' ot poverhnosti morya i vzmyvali v
prostranstvo. Drugie shary priletali otkuda-to iz prostranstva, vrezalis' v
zhidkost' i ischezali pod tysyachami drugih sharov. Vglyadevshis' v prostiravsheesya
vokrug more, Mod uvidela, chto tumannye shary v dejstvitel'nosti byli dvuh
razlichnyh sortov. Bol'shinstvo sharov napominalo po vneshnemu vidu tennisnye
myachi, odnako vstrechalis' i shary pokrupnee. Oni byli bolee prodolgovatymi i
po forme napominali myachi dlya amerikanskogo futbola. Vse shary byli
poluprozrachnymi i imeli slozhnuyu vnutrennyuyu, strukturu, kotoruyu Mod nikak ne
udavalos' razglyadet'.
- Gde my? - proiznesla Mod, zadyhayas'. - Neuzheli tak vyglyadit ad?
- Net, - ulybnulsya v otvet demon. - Vse gorazdo bolee prozaichno. Prosto
my s vami vidim pod ochen' bol'shim uvelicheniem krohotnyj uchastok poverhnosti
zhidkosti v bokale, s pomoshch'yu kotorogo vash muzh dovol'no uspeshno pytaetsya ne
usnut', poka vash batyushka razglagol'stvuet o kvaziergodicheskih sistemah. Vse
eti shary - molekuly. Te, chto pomen'she, - molekuly vody, te, chto pobol'she, -
molekuly spirta. Podschitav, esli ugodno, proporciyu mezhdu temi i drugimi, vy
smozhete opredelit' krepost' napitka, kotoryj smeshal sebe vash muzh.
- _Ochen'_ interesno! - zametila Mod kak mozhno bolee strogim golosom. -
A chto eto za shtukoviny plavayut tam vdali? Oni napominayut paru rezvyashchihsya
kitov. Mozhet byt', eto kakie-nibud' atomnye kity?
Demon vzglyanul v tom napravlenii, kuda ukazyvala Mod.
- Prosto prodemonstrirovat' emu, chto esli ya zahochu, to mogu narushit'
princip vozrastaniya entropii. A chtoby i vy mogli ubedit'sya v etom, ya byl by
ochen' priznatelen vam, esli by vy sostavili mne kompaniyu. Smeyu uverit' vas,
chto vam ne ugrozhaet nikakaya opasnost'.
Pri etih slovah Mod pochuvstvovala, kak demon krepko vzyal ee pod ruku i
vse predmety vokrug slovno soshli s uma. Stol, stul'ya i vsya prochaya obstanovka
stolovoj vdrug nachali s chudovishchnoj skorost'yu uvelichivat'sya, i na ee glazah
spinka kresla, vyrosshaya do gigantskih razmerov, zakryla gorizont. Kogda vse
vokrug postepenno uspokoilos', Mod obnaruzhila, chto plavaet v vozduhe,
podderzhivaemaya svoim neobychnym sputnikom. Kakie-to tumannye shary razmerom s
tennisnyj myach so svistom pronosilis' mimo po vsem napravleniyam. Demon
Maksvella predusmotritel'no predotvrashchal ih ot stolknoveniya so vsemi
malo-mal'ski opasnymi predmetami. Vzglyanuv vniz, Mod uvidela nechto vrode
rybackoj lodki, do samyh uklyuchin gruzhenoj trepyhayushchejsya, bleshchushchej serebrom
ryboj. Prismotrevshis' povnimatel'nee, Mod uvidela, chto eto byli ne ryby, a
mnozhestvo tumannyh sharov, vrode teh, chto to i delo proletali mimo, so
svistom rassekaya vozduh. Demon, po-prezhnemu krepko derzha ee pod ruku, vlek
ee za soboj do teh por, poka oni ne ochutilis' v more kakoj-to zernistoj
zhidkosti, besformennoj i v to zhe vremya podvizhnoj. SHary pryamo-taki kipeli u
samoj poverhnosti morya, a nekotoryh zhidkost' zasasyvala, i oni skryvalis' v
puchine. Vremya ot vremeni nekotorye shary vsplyvali k samoj poverhnosti s
takoj skorost'yu, chto otryvalis' ot poverhnosti morya i vzmyvali v
prostranstvo. Drugie shary priletali otkuda-to iz prostranstva, vrezalis' v
zhidkost' i ischezali pod tysyachami drugih sharov. Vglyadevshis' v prostiravsheesya
vokrug more, Mod uvidela, chto tumannye shary v dejstvitel'nosti byli dvuh
razlichnyh sortov. Bol'shinstvo sharov napominalo po vneshnemu vidu tennisnye
myachi, odnako vstrechalis' i shary pokrupnee. Oni byli bolee prodolgovatymi i
po forme napominali myachi dlya amerikanskogo futbola. Vse shary byli
poluprozrachnymi i imeli slozhnuyu vnutrennyuyu, strukturu, kotoruyu Mod nikak ne
udavalos' razglyadet'.
- Gde my? - proiznesla Mod, zadyhayas'. - Neuzheli tak vyglyadit ad?
- Net, - ulybnulsya v otvet demon. - Vse gorazdo bolee prozaichno. Prosto
my s vami vidim pod ochen' bol'shim uvelicheniem krohotnyj uchastok poverhnosti
zhidkosti v bokale, s pomoshch'yu kotorogo vash muzh dovol'no uspeshno pytaetsya ne
usnut', poka vash batyushka razglagol'stvuet o kvaziergodicheskih sistemah. Vse
eti shary - molekuly. Te, chto pomen'she, - molekuly vody, te, chto pobol'she, -
molekuly spirta. Podschitav, esli ugodno, proporciyu mezhdu temi i drugimi, vy
smozhete opredelit' krepost' napitka, kotoryj smeshal sebe vash muzh.
- _Ochen'_ interesno! - zametila Mod kak mozhno bolee strogim golosom. -
A chto eto za shtukoviny plavayut tam vdali? Oni napominayut paru rezvyashchihsya
kitov. Mozhet byt', eto kakie-nibud' atomnye kity?
Demon vzglyanul v tom napravlenii, kuda ukazyvala Mod.
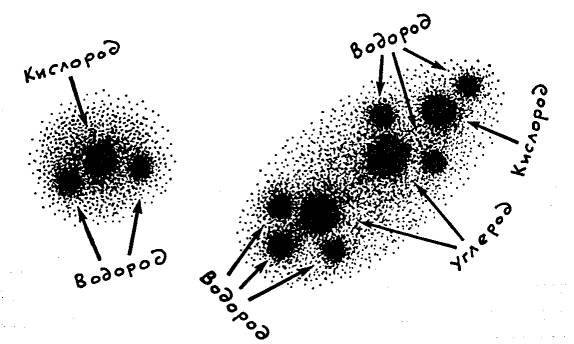 - Net, eto ne kity, - zametil on. - |to krohotnye kusochki podgorevshego
yachmenya - togo samogo ingredienta, kotoryj pridaet viski osobyj vkus i cvet.
Kazhdyj takoj kusochek sostoit iz millionov i millionov slozhnyh organicheskih
molekul, imeet sravnitel'no bol'shie razmery i dovol'no tyazhel. To, chto oni
prygayut na poverhnosti zhidkosti, ob座asnyaetsya dejstviem teh udarov, kotorye
oni poluchayut ot molekul vody i spirta, sovershayushchih teplovoe dvizhenie. Imenno
izuchenie takih chastic srednih razmerov, dostatochno malyh dlya togo, chtoby
oshchushchat' dvizhenie molekul, i vmeste s tem dostatochno bol'shih dlya togo, chtoby
ih mozhno bylo nablyudat' v sil'nyj mikroskop, dalo uchenym pervoe pryamoe
dokazatel'stvo pravil'nosti osnovnyh polozhenij kineticheskoj teorii gazov.
Izmeryaya intensivnost' tarantelly, ispolnyaemoj krohotnymi chasticami,
vzveshennymi v zhidkosti, - ih brounovskogo dvizheniya, kak obychno prinyato
nazyvat' besporyadochnoe dvizhenie takih chastic, fiziki nauchilis' izvlekat'
neposredstvennuyu informaciyu ob energii dvizheniya molekul.
Demon snova povlek za soboj Mod. Oni neslis' po vozduhu do teh por,
poka pered nimi ne voznikla gigantskaya stena, slozhennaya iz beschislennyh
molekul vody. Molekuly byli podognany drug k drugu tochno i plotno, kak
kirpichi.
- Kakoe porazitel'noe zrelishche! - vskrichala Mod. - Kakoj prekrasnyj fon
dlya portreta, kotoryj ya sejchas risuyu! Kstati, a chto eto za zdanie?
- Pered vami fragment kristalla l'da, odin iz mnogih kristallikov,
obrazuyushchih kubik l'da v stakane vashego muzha, - skazal demon. - A teper',
proshu proshcheniya, samoe vremya nachat' pridumannyj mnoj rozygrysh i podshutit' nad
starym samouverennym professorom.
S etimi slovami demon ostavil Mod na rebre kristalla l'da, napodobie
al'pinista, vzgromozdivshegosya na gornyj hrebet, i pristupil k rabote.
Vooruzhivshis' instrumentom napodobie tennisnoj raketki, demon prinyalsya
otbivat' proletavshie mimo molekuly. Bystro peremeshchayas' s mesta na mesto, on
pospeval vovremya, chtoby otbit' upryamuyu molekulu, uporno prodolzhavshuyu
dvigat'sya v nepravil'nom napravlenii. Nesmotrya na opasnost' svoego polozheniya
Mod ne mogla ne voshishchat'sya provorstvom i lovkost'yu demona i dazhe
podbadrivala ego vozglasami, kogda emu udavalos' otbit' osobenno bystruyu i
trudnuyu molekulu. Po sravneniyu s tem, chto vytvoryal demon, samye znamenitye
chempiony po tennisu vyglyadeli zhalkimi, beznadezhno neuklyuzhimi uval'nyami. Ne
proshlo i neskol'kih minut, kak rezul'taty raboty Demona stali zametny.
Teper', hotya chast' poverhnosti zhidkosti byla pokryta ochen' medlenno
dvizhushchimisya spokojnymi molekulami, drugaya chast' poverhnosti, raspolozhennaya
pryamo u Mod pod nogami, kishela molekulami, yarostno snovavshimi po vsem
napravleniyam. CHislo molekul, pokidavshih poverhnost' v processe ispareniya.
bystro narastalo. Molekuly pokidali zhidkost' bol'shimi gruppami po tysyache
molekul i bolee, proryvayas' skvoz' poverhnost' zhidkosti v vide bol'shih
puzyrej. Vskore oblako para skrylo ot Mod vse i lish' vremya ot vremeni ona
mogla razlichit' razyashchie vzmahi raketki i faldy fraka, v kotoryj byl oblachen
demon, sredi besnuyushchihsya molekul. Nakonec, molekuly na tom fragmente l'da,
na kotorom ona vossedala, poddalis', i Mod stala padat' skvoz' tyazhelye
oblaka para, rasstilavshiesya pod nej...
- Net, eto ne kity, - zametil on. - |to krohotnye kusochki podgorevshego
yachmenya - togo samogo ingredienta, kotoryj pridaet viski osobyj vkus i cvet.
Kazhdyj takoj kusochek sostoit iz millionov i millionov slozhnyh organicheskih
molekul, imeet sravnitel'no bol'shie razmery i dovol'no tyazhel. To, chto oni
prygayut na poverhnosti zhidkosti, ob座asnyaetsya dejstviem teh udarov, kotorye
oni poluchayut ot molekul vody i spirta, sovershayushchih teplovoe dvizhenie. Imenno
izuchenie takih chastic srednih razmerov, dostatochno malyh dlya togo, chtoby
oshchushchat' dvizhenie molekul, i vmeste s tem dostatochno bol'shih dlya togo, chtoby
ih mozhno bylo nablyudat' v sil'nyj mikroskop, dalo uchenym pervoe pryamoe
dokazatel'stvo pravil'nosti osnovnyh polozhenij kineticheskoj teorii gazov.
Izmeryaya intensivnost' tarantelly, ispolnyaemoj krohotnymi chasticami,
vzveshennymi v zhidkosti, - ih brounovskogo dvizheniya, kak obychno prinyato
nazyvat' besporyadochnoe dvizhenie takih chastic, fiziki nauchilis' izvlekat'
neposredstvennuyu informaciyu ob energii dvizheniya molekul.
Demon snova povlek za soboj Mod. Oni neslis' po vozduhu do teh por,
poka pered nimi ne voznikla gigantskaya stena, slozhennaya iz beschislennyh
molekul vody. Molekuly byli podognany drug k drugu tochno i plotno, kak
kirpichi.
- Kakoe porazitel'noe zrelishche! - vskrichala Mod. - Kakoj prekrasnyj fon
dlya portreta, kotoryj ya sejchas risuyu! Kstati, a chto eto za zdanie?
- Pered vami fragment kristalla l'da, odin iz mnogih kristallikov,
obrazuyushchih kubik l'da v stakane vashego muzha, - skazal demon. - A teper',
proshu proshcheniya, samoe vremya nachat' pridumannyj mnoj rozygrysh i podshutit' nad
starym samouverennym professorom.
S etimi slovami demon ostavil Mod na rebre kristalla l'da, napodobie
al'pinista, vzgromozdivshegosya na gornyj hrebet, i pristupil k rabote.
Vooruzhivshis' instrumentom napodobie tennisnoj raketki, demon prinyalsya
otbivat' proletavshie mimo molekuly. Bystro peremeshchayas' s mesta na mesto, on
pospeval vovremya, chtoby otbit' upryamuyu molekulu, uporno prodolzhavshuyu
dvigat'sya v nepravil'nom napravlenii. Nesmotrya na opasnost' svoego polozheniya
Mod ne mogla ne voshishchat'sya provorstvom i lovkost'yu demona i dazhe
podbadrivala ego vozglasami, kogda emu udavalos' otbit' osobenno bystruyu i
trudnuyu molekulu. Po sravneniyu s tem, chto vytvoryal demon, samye znamenitye
chempiony po tennisu vyglyadeli zhalkimi, beznadezhno neuklyuzhimi uval'nyami. Ne
proshlo i neskol'kih minut, kak rezul'taty raboty Demona stali zametny.
Teper', hotya chast' poverhnosti zhidkosti byla pokryta ochen' medlenno
dvizhushchimisya spokojnymi molekulami, drugaya chast' poverhnosti, raspolozhennaya
pryamo u Mod pod nogami, kishela molekulami, yarostno snovavshimi po vsem
napravleniyam. CHislo molekul, pokidavshih poverhnost' v processe ispareniya.
bystro narastalo. Molekuly pokidali zhidkost' bol'shimi gruppami po tysyache
molekul i bolee, proryvayas' skvoz' poverhnost' zhidkosti v vide bol'shih
puzyrej. Vskore oblako para skrylo ot Mod vse i lish' vremya ot vremeni ona
mogla razlichit' razyashchie vzmahi raketki i faldy fraka, v kotoryj byl oblachen
demon, sredi besnuyushchihsya molekul. Nakonec, molekuly na tom fragmente l'da,
na kotorom ona vossedala, poddalis', i Mod stala padat' skvoz' tyazhelye
oblaka para, rasstilavshiesya pod nej...
 Kogda oblaka rasseyalis', Mod obnaruzhila, chto sidit v tom samom kresle,
v kotorom sidela pered tem, kak vyjti v stolovuyu.
- Svyataya entropiya! - voskliknul vdrug otec Mod, glyadya na vysokij bokal,
stoyavshij pered misterom Tompkinsom. - Da ved' zhidkost' kipit!
Dejstvitel'no, zhidkost' v bokale pokrylas' lopayushchimisya puzyryami, i k
potolku nad bokalom medlenno podnimalas' tonkoe oblachko para. Bylo stranno,
odnako, chto napitok v stakane kipel lish' na sravnitel'no malom uchastke
vokrug kubika l'da. Ves' ostal'noj napitok byl sovershenno holodnym.
- Net, vy tol'ko podumajte! - prodolzhal professor sevshim ot volneniya
drozhashchim golosom. - YA rasskazyvayu vam o statisticheskih fluktuaciyah v
vozrastanii entropii, i, pozhalujsta, takaya fluktuaciya pered nami! V
rezul'tate neveroyatnogo stecheniya obstoyatel'stv vpervye s sotvoreniya Zemli
bolee bystrye molekuly sluchajno sobralis' na odnom uchastke poverhnosti
zhidkosti, i zhidkost' sama soboj zakipela! V blizhajshie milliardy let my s
vami ostanemsya edinstvennymi lyud'mi, kotorym poschastlivilos' videt' eto
neobychajnoe yavlenie.
Professor ne otryval glaz ot napitka, kotoryj teper' medlenno ostyval.
- Kakaya udacha! - vzdohnul on s schastlivoj ulybkoj. - Kakoe
neobyknovennoe vezenie!
Mod ulybnulas', no nichego ne skazala. Zachem ej bylo sporit' s otcom,
esli na etot raz ona tochno znala, chto istinnaya prichina yavleniya byla izvestna
ej luchshe, chem emu.
Glava 10
Veseloe plemya elektronov
CHerez neskol'ko dnej, zakanchivaya obed, mister Tompkins vspomnil, chto
vecherom dolzhna sostoyat'sya lekciya professora o stroenii atoma, kotoruyu on
obeshchal posetit'. No malovrazumitel'nymi ob座asneniyami svoego testya mister
Tompkins byl syt po gorlo, i poetomu reshil propustit' lekciyu i skorotat'
vecherok doma. No kogda on ustraivalsya poudobnee v svoem kresle, mechtaya
pochitat' interesnuyu knigu, Mod otrezala etot put' k otstupleniyu: vzglyanuv na
chasy, ona zayavila myagko, no tonom, ne dopuskayushchim vozrazhenij, chto misteru
Tompkinsu pora otpravlyat'sya na lekciyu. I cherez kakih-nibud' polchasa mister
Tompkins sidel na zhestkoj derevyannoj skam'e vmeste s tolpoj gorazdo bolee
molodyh studentov.
- Ledi i dzhentl'meny, - nachal professor, strogo glyadya na slushatelej
poverh ochkov, - na proshloj lekcii ya obeshchal vam podrobnee rasskazat' o
vnutrennem stroenii atoma i ob座asnit', kakim obrazom te ili inye konkretnye
osobennosti ego stroeniya obuslavlivayut razlichnye fizicheskie i himicheskie
svojstva atoma. Vy, konechno, znaete, chto atomy ne rassmatrivayutsya bolee kak
elementarnye nedelimye sostavnye chasti materii i chto eta rol' nyne pereshla k
gorazdo men'shim chasticam - elektronam, protonam i t. d.
Predstavlenie ob elementarnyh sostavlyayushchih materii kak o poslednej
stupeni v delimosti material'nyh tel voshodit k drevnegrecheskomu filosofu
Demokritu, zhivshemu v IV veke do n. e. Razmyshlyaya o skrytoj prirode veshchej,
Demokrit prishel k probleme stroeniya materii i stolknulsya s voprosom o tom,
mozhet ili ne mozhet sushchestvovat' beskonechno malaya porciya materii. Poskol'ku v
tu dalekuyu epohu lyubuyu problemu imeli obyknovenie reshat' lish'
odnim-edinstvennym sposobom - s pomoshch'yu chistogo myshleniya i k tomu zhe vopros
v to vremya nahodilsya daleko za ramkami vozmozhnostej resheniya ego
eksperimental'nymi metodami, Demokrit v poiskah pravil'nogo otveta opustilsya
v glubiny sobstvennogo razuma. Ishodya iz nekotoryh dovol'no smutnyh
filosofskih soobrazhenij, on v konce koncov prishel k vyvodu o tom, chto
"nemyslimo", chtoby materiya bezgranichno delilas' na vse bolee i bolee melkie
porcii, i chto poetomu neobhodimo prinyat' predpolozhenie o sushchestvovanii
"naimen'shih chastic, kotorye ne dopuskayut dal'nejshego deleniya". Takie chasticy
Demokrit nazval atomami, chto, kak vy, vozmozhno, znaete, oznachaet po-grecheski
"nedelimye".
YA otnyud' ne hochu priumen'shat' velichie vklada Demokrita v razvitie
estestvennyh nauk, odnako spravedlivosti radi hotel by obratit' vashe
vnimanie na to, chto naryadu s Demokritom i ego posledovatelyami v
drevnegrecheskoj filosofii sushchestvovala i drugaya shkola, priverzhency kotoroj
schitali, chto process deleniya _neogranichenno prodolzhaem_. Poetomu nezavisimo
ot togo, kakoj otvet na etot vopros dast v budushchem tochnoe estestvoznanie,
drevnegrecheskoj filosofii obespecheno pochetnoe mesto v istorii fiziki. Vo
vremena Demokrita i dazhe mnogo stoletij spustya sushchestvovanie takih nedelimyh
porcij materii rassmatrivalos' kak chisto filosofskaya gipoteza, i tol'ko v
XIX veke uchenye reshili, chto im, nakonec, udalos' obnaruzhit' te nedelimye
kirpichiki materii, sushchestvovanie kotoryh bylo predskazano drevnegrecheskimi
filosofami za dve tysyachi let do razygravshihsya sobytij.
V 1808 g. anglijskij himik Dzhon Dal'ton ustanovil tak nazyvaemyj zakon
kratnyh otnoshenij. On pokazal, chto...
Pochti s samogo nachala lekcii mistera Tompkinsa neuderzhimo klonilo v
son. Emu ochen' hotelos' somknut' glaza i, prebyvaya v priyatnoj dremote,
dosidet' do konca lekcii, no meshala lish' surovaya zhestkost' universitetskoj
skam'i. No otkrytyj Dal'tonom zakon kratnyh otnoshenij okazalsya poslednej
solominkoj, perelomivshej spinu verblyudu, i v pritihshej auditorii vskore
mozhno bylo otchetlivo razlichit' tonkoe posvistyvanie, donosivsheesya iz ugla,
gde sidel mister Tompkins.
Kogda oblaka rasseyalis', Mod obnaruzhila, chto sidit v tom samom kresle,
v kotorom sidela pered tem, kak vyjti v stolovuyu.
- Svyataya entropiya! - voskliknul vdrug otec Mod, glyadya na vysokij bokal,
stoyavshij pered misterom Tompkinsom. - Da ved' zhidkost' kipit!
Dejstvitel'no, zhidkost' v bokale pokrylas' lopayushchimisya puzyryami, i k
potolku nad bokalom medlenno podnimalas' tonkoe oblachko para. Bylo stranno,
odnako, chto napitok v stakane kipel lish' na sravnitel'no malom uchastke
vokrug kubika l'da. Ves' ostal'noj napitok byl sovershenno holodnym.
- Net, vy tol'ko podumajte! - prodolzhal professor sevshim ot volneniya
drozhashchim golosom. - YA rasskazyvayu vam o statisticheskih fluktuaciyah v
vozrastanii entropii, i, pozhalujsta, takaya fluktuaciya pered nami! V
rezul'tate neveroyatnogo stecheniya obstoyatel'stv vpervye s sotvoreniya Zemli
bolee bystrye molekuly sluchajno sobralis' na odnom uchastke poverhnosti
zhidkosti, i zhidkost' sama soboj zakipela! V blizhajshie milliardy let my s
vami ostanemsya edinstvennymi lyud'mi, kotorym poschastlivilos' videt' eto
neobychajnoe yavlenie.
Professor ne otryval glaz ot napitka, kotoryj teper' medlenno ostyval.
- Kakaya udacha! - vzdohnul on s schastlivoj ulybkoj. - Kakoe
neobyknovennoe vezenie!
Mod ulybnulas', no nichego ne skazala. Zachem ej bylo sporit' s otcom,
esli na etot raz ona tochno znala, chto istinnaya prichina yavleniya byla izvestna
ej luchshe, chem emu.
Glava 10
Veseloe plemya elektronov
CHerez neskol'ko dnej, zakanchivaya obed, mister Tompkins vspomnil, chto
vecherom dolzhna sostoyat'sya lekciya professora o stroenii atoma, kotoruyu on
obeshchal posetit'. No malovrazumitel'nymi ob座asneniyami svoego testya mister
Tompkins byl syt po gorlo, i poetomu reshil propustit' lekciyu i skorotat'
vecherok doma. No kogda on ustraivalsya poudobnee v svoem kresle, mechtaya
pochitat' interesnuyu knigu, Mod otrezala etot put' k otstupleniyu: vzglyanuv na
chasy, ona zayavila myagko, no tonom, ne dopuskayushchim vozrazhenij, chto misteru
Tompkinsu pora otpravlyat'sya na lekciyu. I cherez kakih-nibud' polchasa mister
Tompkins sidel na zhestkoj derevyannoj skam'e vmeste s tolpoj gorazdo bolee
molodyh studentov.
- Ledi i dzhentl'meny, - nachal professor, strogo glyadya na slushatelej
poverh ochkov, - na proshloj lekcii ya obeshchal vam podrobnee rasskazat' o
vnutrennem stroenii atoma i ob座asnit', kakim obrazom te ili inye konkretnye
osobennosti ego stroeniya obuslavlivayut razlichnye fizicheskie i himicheskie
svojstva atoma. Vy, konechno, znaete, chto atomy ne rassmatrivayutsya bolee kak
elementarnye nedelimye sostavnye chasti materii i chto eta rol' nyne pereshla k
gorazdo men'shim chasticam - elektronam, protonam i t. d.
Predstavlenie ob elementarnyh sostavlyayushchih materii kak o poslednej
stupeni v delimosti material'nyh tel voshodit k drevnegrecheskomu filosofu
Demokritu, zhivshemu v IV veke do n. e. Razmyshlyaya o skrytoj prirode veshchej,
Demokrit prishel k probleme stroeniya materii i stolknulsya s voprosom o tom,
mozhet ili ne mozhet sushchestvovat' beskonechno malaya porciya materii. Poskol'ku v
tu dalekuyu epohu lyubuyu problemu imeli obyknovenie reshat' lish'
odnim-edinstvennym sposobom - s pomoshch'yu chistogo myshleniya i k tomu zhe vopros
v to vremya nahodilsya daleko za ramkami vozmozhnostej resheniya ego
eksperimental'nymi metodami, Demokrit v poiskah pravil'nogo otveta opustilsya
v glubiny sobstvennogo razuma. Ishodya iz nekotoryh dovol'no smutnyh
filosofskih soobrazhenij, on v konce koncov prishel k vyvodu o tom, chto
"nemyslimo", chtoby materiya bezgranichno delilas' na vse bolee i bolee melkie
porcii, i chto poetomu neobhodimo prinyat' predpolozhenie o sushchestvovanii
"naimen'shih chastic, kotorye ne dopuskayut dal'nejshego deleniya". Takie chasticy
Demokrit nazval atomami, chto, kak vy, vozmozhno, znaete, oznachaet po-grecheski
"nedelimye".
YA otnyud' ne hochu priumen'shat' velichie vklada Demokrita v razvitie
estestvennyh nauk, odnako spravedlivosti radi hotel by obratit' vashe
vnimanie na to, chto naryadu s Demokritom i ego posledovatelyami v
drevnegrecheskoj filosofii sushchestvovala i drugaya shkola, priverzhency kotoroj
schitali, chto process deleniya _neogranichenno prodolzhaem_. Poetomu nezavisimo
ot togo, kakoj otvet na etot vopros dast v budushchem tochnoe estestvoznanie,
drevnegrecheskoj filosofii obespecheno pochetnoe mesto v istorii fiziki. Vo
vremena Demokrita i dazhe mnogo stoletij spustya sushchestvovanie takih nedelimyh
porcij materii rassmatrivalos' kak chisto filosofskaya gipoteza, i tol'ko v
XIX veke uchenye reshili, chto im, nakonec, udalos' obnaruzhit' te nedelimye
kirpichiki materii, sushchestvovanie kotoryh bylo predskazano drevnegrecheskimi
filosofami za dve tysyachi let do razygravshihsya sobytij.
V 1808 g. anglijskij himik Dzhon Dal'ton ustanovil tak nazyvaemyj zakon
kratnyh otnoshenij. On pokazal, chto...
Pochti s samogo nachala lekcii mistera Tompkinsa neuderzhimo klonilo v
son. Emu ochen' hotelos' somknut' glaza i, prebyvaya v priyatnoj dremote,
dosidet' do konca lekcii, no meshala lish' surovaya zhestkost' universitetskoj
skam'i. No otkrytyj Dal'tonom zakon kratnyh otnoshenij okazalsya poslednej
solominkoj, perelomivshej spinu verblyudu, i v pritihshej auditorii vskore
mozhno bylo otchetlivo razlichit' tonkoe posvistyvanie, donosivsheesya iz ugla,
gde sidel mister Tompkins.
 Kogda mister Tompkins ochnulsya ot sna, neudobstvo sideniya na zhestkoj
skam'e smenilos' priyatnym oshchushcheniem pareniya v vozduhe. Otkryv glaza, mister
Tompkins s udivleniem obnaruzhil, chto mchitsya v prostranstve s legkomyslenno,
kak emu pokazalos', bol'shoj skorost'yu. Oglyanuvshis' po storonam, mister
Tompkins uvidel, chto on ne odinok v svoem fantasticheskom puteshestvii.
Nepodaleku ot nego neskol'ko rasplyvchatyh smutnyh sushchestv obrashchalis' vokrug
bol'shogo tyazhelogo na vid ob容kta v centre horovoda. |to strannye prizrachnye
sushchestva mchalis' parami, veselo gonyayas' drug za drugom po krugovym i
ellipticheskim traektoriyam. Vnezapno mister Tompkins pochuvstvoval sebya ochen'
odinokim, osoznav, chto lish' u nego odnogo net partnera.
- Pochemu ya ne vzyal s soboj Mod? - tosklivo podumal mister Tompkins. -
My by chudesno proveli vremya v etom horovode.
Traektoriya, po kotoroj dvigalsya mister Tompkins, prolegala v storone ot
traektorij ostal'nyh sushchestv, ohvatyvaya ih snaruzhi, i hotya misteru
Tompksinsu ochen' hotelos' prisoedinit'sya k ostal'noj kompanii, nepriyatnoe
chuvstvo postoronnego uderzhivalo i meshalo emu sdelat' shag navstrechu veselym
puteshestvennikam. Odnako kogda odnomu iz elektronov (k tomu vremeni mister
Tompkins okonchatel'no ponyal, chto nepostizhimym i chudesnym obrazom
prisoedinilsya k soobshchestvu elektronov, naselyavshih kakoj-to atom) sluchilos'
proletet' nepodaleku ot nego po sil'no vytyanutoj orbite, mister Tompkins
reshil pozhalovat'sya na svoi neudachi.
- Pochemu u menya net partnera dlya igr i zabav? - prokrichal on vsled
elektronu.
- Potomu, chto eto nechetnyj atom, a vy valentnyj elektro-o-n, -
doneslos' v otvet. S etimi slovami elektron povernul i ustremilsya v tolpu
plyashushchih elektronov.
- Valentnye elektrony zhivut v odinochku ili nahodyat sebe kompan'onov v
drugih atomah, - propishchal vysokim fal'cetom drugoj elektron, pronosyas' mimo
mistera Tompkinsa.
"Esli nuzhen kompan'on,
Znajte: v hlore zhdet vas on", -
nasmeshlivo propel tretij.
- Vizhu, vy zdes' novichok, syn moj, i ochen' odinoki, - razdalsya nad
misterom Tompkinsom druzheskij golos, i, vozvedya glaza gore, nash geroj uvidel
plotnuyu figuru monaha v korichnevoj sutane.
- YA otec Paulini, - prodolzhal monah, dvigayas' po traektorii vmeste s
misterom Tompkinsom, - i moya missiya v etoj zhizni sostoit v tom, chtoby
nablyudat' za moral'yu i social'nym povedeniem elektronov v atomah i povsyudu.
Moj dolg - sledit' za tem, chtoby vse eti bezzabotnye i igrivye elektrony
byli nadlezhashchim obrazom raspredeleny po razlichnym kvantovym kel'yam etogo
prekrasnogo atomnogo stroeniya, vozdvignutogo nashim velikim arhitektorom
Nil'som Borom. Daby podderzhivat' poryadok i sohranyat' svojstva, ya nikogda ne
razreshayu nahodit'sya na odnoj i toj zhe traektorii bolee chem dvum elektronam.
Stoit im sobrat'sya vtroem, kak hlopot ne oberesh'sya. Poetomu elektrony vsegda
sgruppirovany v pary s protivopolozhnym "spinom", i esli takaya para
poselyaetsya v kel'e, to tret'emu elektronu ne razreshaetsya narushat' ih pokoj.
|to horoshee pravilo, i ya mogu dobavit', chto do sih por ni odin elektron ne
narushil vvedenogo mnoj rasporyadka.
Kogda mister Tompkins ochnulsya ot sna, neudobstvo sideniya na zhestkoj
skam'e smenilos' priyatnym oshchushcheniem pareniya v vozduhe. Otkryv glaza, mister
Tompkins s udivleniem obnaruzhil, chto mchitsya v prostranstve s legkomyslenno,
kak emu pokazalos', bol'shoj skorost'yu. Oglyanuvshis' po storonam, mister
Tompkins uvidel, chto on ne odinok v svoem fantasticheskom puteshestvii.
Nepodaleku ot nego neskol'ko rasplyvchatyh smutnyh sushchestv obrashchalis' vokrug
bol'shogo tyazhelogo na vid ob容kta v centre horovoda. |to strannye prizrachnye
sushchestva mchalis' parami, veselo gonyayas' drug za drugom po krugovym i
ellipticheskim traektoriyam. Vnezapno mister Tompkins pochuvstvoval sebya ochen'
odinokim, osoznav, chto lish' u nego odnogo net partnera.
- Pochemu ya ne vzyal s soboj Mod? - tosklivo podumal mister Tompkins. -
My by chudesno proveli vremya v etom horovode.
Traektoriya, po kotoroj dvigalsya mister Tompkins, prolegala v storone ot
traektorij ostal'nyh sushchestv, ohvatyvaya ih snaruzhi, i hotya misteru
Tompksinsu ochen' hotelos' prisoedinit'sya k ostal'noj kompanii, nepriyatnoe
chuvstvo postoronnego uderzhivalo i meshalo emu sdelat' shag navstrechu veselym
puteshestvennikam. Odnako kogda odnomu iz elektronov (k tomu vremeni mister
Tompkins okonchatel'no ponyal, chto nepostizhimym i chudesnym obrazom
prisoedinilsya k soobshchestvu elektronov, naselyavshih kakoj-to atom) sluchilos'
proletet' nepodaleku ot nego po sil'no vytyanutoj orbite, mister Tompkins
reshil pozhalovat'sya na svoi neudachi.
- Pochemu u menya net partnera dlya igr i zabav? - prokrichal on vsled
elektronu.
- Potomu, chto eto nechetnyj atom, a vy valentnyj elektro-o-n, -
doneslos' v otvet. S etimi slovami elektron povernul i ustremilsya v tolpu
plyashushchih elektronov.
- Valentnye elektrony zhivut v odinochku ili nahodyat sebe kompan'onov v
drugih atomah, - propishchal vysokim fal'cetom drugoj elektron, pronosyas' mimo
mistera Tompkinsa.
"Esli nuzhen kompan'on,
Znajte: v hlore zhdet vas on", -
nasmeshlivo propel tretij.
- Vizhu, vy zdes' novichok, syn moj, i ochen' odinoki, - razdalsya nad
misterom Tompkinsom druzheskij golos, i, vozvedya glaza gore, nash geroj uvidel
plotnuyu figuru monaha v korichnevoj sutane.
- YA otec Paulini, - prodolzhal monah, dvigayas' po traektorii vmeste s
misterom Tompkinsom, - i moya missiya v etoj zhizni sostoit v tom, chtoby
nablyudat' za moral'yu i social'nym povedeniem elektronov v atomah i povsyudu.
Moj dolg - sledit' za tem, chtoby vse eti bezzabotnye i igrivye elektrony
byli nadlezhashchim obrazom raspredeleny po razlichnym kvantovym kel'yam etogo
prekrasnogo atomnogo stroeniya, vozdvignutogo nashim velikim arhitektorom
Nil'som Borom. Daby podderzhivat' poryadok i sohranyat' svojstva, ya nikogda ne
razreshayu nahodit'sya na odnoj i toj zhe traektorii bolee chem dvum elektronam.
Stoit im sobrat'sya vtroem, kak hlopot ne oberesh'sya. Poetomu elektrony vsegda
sgruppirovany v pary s protivopolozhnym "spinom", i esli takaya para
poselyaetsya v kel'e, to tret'emu elektronu ne razreshaetsya narushat' ih pokoj.
|to horoshee pravilo, i ya mogu dobavit', chto do sih por ni odin elektron ne
narushil vvedenogo mnoj rasporyadka.
 - Mozhet byt', eto _ochen'_ horoshee pravilo, - vozrazil mister Tompkins,
- no v dannyj moment ya terplyu iz-za nego bol'shie neudobstva.
- Vizhu, syn moj, - ulybnulsya monah, - no vam prosto ne povezlo.
Ugorazdilo zhe vas stat' valentnym elektronom v atome s nechetnym atomnym
nomerom. Atom natriya, kotoromu vy prinadlezhite, obyazan imet' iz-za
elektricheskogo zaryada svoego yadra (toj bol'shoj temnoj massy, kotoruyu vy
vidite v centre) odinnadcat' elektronov. K velichajshemu sozhaleniyu dlya vas,
odinnadcat' - chislo nechetnoe, chto samo po sebe ne takaya uzh redkost', esli
prinyat' vo vnimanie, chto rovno polovina vseh celyh chisel nechetna i tol'ko
drugaya polovina chetna. Tak chto vam pridetsya kak poyavivshemusya poslednim po
krajnej mere kakoe-to vremya pobyt' odnomu.
- Vy hotite skazat', chto pozdnee u menya, vozmozhno, poyavitsya shans
obzavestis' partnerom? - s nadezhdoj sprosil mister Tompkins. - Naprimer,
vybit' s orbity kogo-nibud' iz elektronov-pervoposelencev?
- |to delaetsya ne tak, - vozrazil monah, grozya misteru Tomgasinsu
korotkim tolstym pal'cem, - no vsegda est' shans, chto kakoj-nibud' iz
elektronov, obrashchayushchihsya po vnutrennim orbitam, budet vybroshen vneshnim
vozmushcheniem i ostavit posle sebya ne zanyatoe mesto, ili vakansiyu. No na vashem
meste ya ne stal by na eto osobenno rasschityvat'.
- |lektrony skazali mne, chto bylo by luchshe, esli by ya pronik v atom
hlora, - skazal mister Tompkins, neskol'ko obeskurazhennyj slovami otca
Paulini. - Mozhete li vy posovetovat' mne, kak eto luchshe sdelat'?
- Molodoj chelovek, molodoj chelovek! - s sozhaleniem pokachal golovoj
monah. - Nu chto vam tak ne terpitsya najti kompan'ona? Pochemu vy ne mozhete po
dostoinstvu ocenit' prelest' odinochestva i nasladit'sya etoj nisposlannoj
nebom vozmozhnost'yu sozercat' s mirom sobstvennuyu dushu? Pochemu chetnye
elektrony tak sil'no l'nut k mirskoj zhizni? No esli vy nastaivaete na
priobretenii kompan'ona, ya pomogu vam osushchestvit' vashe zhelanie. Vzglyanuv v
tom napravlenii, kuda ya ukazyvayu, vy uvidite priblizhayushchijsya k nam atom
hlora, i dazhe so stol' bol'shogo rasstoyaniya vy mozhete legko razlichit'
svobodnoe mesto, gde vas, nesomnenno, ozhidaet samyj teplyj priem. |to
svobodnoe mesto nahoditsya vo vneshnej gruppe elektronov, tak nazyvaemoj
M-obolochke, kotoraya sostoit iz vos'mi elektronov, razbityh na chetyre pary.
No, kak vy vidite, chetyre elektrona vrashchayutsya vokrug svoih osej v odnom
napravlenii i tol'ko tri - v drugom, poetomu odno mesto ostaetsya vakantnym.
Vnutrennie obolochki, nazyvaemye K- i Z-obolochkami, polnost'yu zapolneny, i
atom budet rad zapoluchit' vas i zapolnit' svoyu vneshnyuyu obolochku. Kak tol'ko
dva atoma sblizyatsya, vy dolzhny prosto pereprygnut' s odnogo atoma na drugoj,
kak eto obychno delayut valentnye elektrony. Da budet mir s vami, syn moj!
S etimi slovami vnushitel'naya figura elektronnogo pastyrya vnezapno
rastvorilas' v razrezhennom vozduhe.
Obodrennyj mister Tompkins sobralsya s silami i sovershil golovolomnyj
pryzhok na orbitu proletavshego mimo atoma hlora. K svoemu udivleniyu, on
prizemlilsya na atome hlora ne bez izyashchestva i srazu zhe okazalsya v druzheskom
okruzhenii elektronov M-obolochki atoma hlora.
- Dobro pozhalovat'! Rady, chto vy prisoedinilis' k nam! - obratilsya k
nemu novyj partner s protivopolozhnym spinom, izyashchno skol'zya vdol' orbity. -
Teper' nikto ne mozhet skazat', chto nashe soobshchestvo nepolno. Teper' my mozhem
velikolepno poveselit'sya vse vmeste!
Mister Tompkins ne mog ne soglasit'sya, chto bylo dejstvitel'no veselo
(vesel'e bilo cherez kraj!), no tut emu v golovu zakralas' odna bespokojnaya
mysl'. - A kak ya ob座asnyu vse eto Mod, kogda snova uvizhu ee?
Vprochem, chuvstvo viny u mistera Tompkinsa vskore rasseyalos'.
- Mod vryad li stala by vozrazhat', - reshil on, - ved' v konce koncov eto
lish' elektrony.
- Pochemu pokinutyj vami atom ne uletaet proch'? - sprosil u mistera
Tompkinsa s nedovol'noj grimasoj ego kompan'on. - On vse eshche nadeetsya na
vashe vozvrashchenie?
Dejstvitel'no, poteryav svoj valentnyj elektron, atom natriya _nakrepko_
prilepilsya k atomu hlora, kak by v nadezhde, chto mister Tompkins peredumaet i
snova vernetsya na svoyu orbitu, po kotoroj on mchalsya v polnom odinochestve.
- Net, kak vam eto nravitsya! - serdito probormotal mister Tompkins,
hmuro glyadya na atom, kotoryj ponachalu prinyal ego tak holodno. - Ne atom, a
kakaya-to sobaka na sene!
- O, oni vsegda vedut sebya tak, eti atomy s nechetnymi nomerami, -
zametil bolee opytnyj chlen M-obolochki. - Naskol'ko ya ponimayu, vashego
vozvrashcheniya zhazhdet ne stol'ko soobshchestvo elektronov atoma natriya, skol'ko
samo yadro etogo atoma. Mezhdu central'nym yadrom i ego elektronnym eskortom
vsegda sushchestvuyut nekotorye raznoglasiya. YAdro hochet imet' vokrug sebya
stol'ko elektronov, skol'ko ono mozhet uderzhat' svoim elektricheskim zaryadom,
v to vremya kak sami elektrony predpochitayut byt' v takom kolichestve, kotoroe
pozvolyaet im do konca zapolnyat' obolochki. Sushchestvuet lish' neskol'ko vidov
atomov, tak nazyvaemye _redkie gazy_, ili, kak nazyvayut ih nemeckie fiziki,
_blagorodnye gazy_, v kotoryh zhazhda vlasti so storony atomnogo yadra i
stremleniya poddannyh-elektronov nahodyatsya v polnoj garmonii. Naprimer, takie
atomy, kak gelij, neon i argon ochen' dovol'ny caryashchim v nih soglasiem mezhdu
yadrom i elektronami i nikogda ne izgonyayut svoih elektronov i ne priglashayut
novyh. Oni himicheski inertny i derzhatsya v storone ot vseh ostal'nyh atomov.
No vo vseh ostal'nyh atomah elektronnye soobshchestva vsegda gotovy obmenyat'sya
svoimi chlenami. V atome natriya, vashem prezhnem obitalishche, svita yadra
naschityvaet na odin elektron bol'she, chem neobhodimo dlya garmonii v
obolochkah. S drugoj storony, v nashem atome normal'naya chislennost'
elektronnogo naseleniya nedostatochna dlya polnoj garmonii, poetomu my ochen'
rady vashemu pribytiyu, nesmotrya na to, chto vashe prisutstvie peregruzhaet nashe
yadro. No pokuda vy ostaetes' s nami, nash atom perestaet byt' nejtral'nym i
poluchaet dopolnitel'nyj elektricheskij zaryad. Poetomu atom natriya, kotoryj vy
pokinuli, prilip k nashemu atomu, uderzhivaemyj siloj elektricheskogo
prityazheniya. Odnazhdy mne dovelos' slyshat' nashego pervosvyashchennika otca
Paulini, i on skazal, chto atomnye soobshchestva s lishnimi ili nedostayushchimi
elektronami nazyvayutsya sootvetstvenno otricatel'nymi i polozhitel'nymi
_ionami_. Otec Paulini ispol'zoval takzhe termin molekula dlya oboznacheniya
grupp iz dvuh ili bolee atomov, uderzhivaemyh vmeste elektricheskoj siloj. V
chastnosti, kombinaciyu iz odnogo atoma natriya i odnogo atoma hlora otec
Paulini nazval molekuloj _povarennoj soli_, hotya ya reshitel'no ne ponimayu,
chto by eto moglo oznachat'.
- Vy hotite skazat', budto ne znaete, chto takoe povarennaya sol'? -
udivlenno sprosil mister Tompkins, zabyv o tom, s kem on razgovarivaet. -
|to tot samyj belyj poroshok, kotorym vy za zavtrakom posypaete yajco vsmyatku.
- A chto takoe yajco vsmyatku i chto takoe zavtrak? - s interesom sprosil
elektron.
Mister Tompkins probormotal chto-to nevnyatnoe i tut tol'ko so vsej
yasnost'yu ponyal vsyu tshchetnost' lyubyh popytok ob座asnit' svoim kompan'onam dazhe
samye nezamyslovatye detali povsednevnoj zhizni lyudej.
- Pochemu-to mne ne udaetsya pocherpnut' dlya sebya nichego novogo iz vseh
etih razgovorov o valentnosti i zapolnennyh obolochkah, - skazal sebe mister
Tompkins, reshiv naslazhdat'sya svoim vizitom v fantasticheskij mir atoma i ne
zabivat' sebe golovu neponyatnymi voprosami. No otdelat'sya ot razgovorchivogo
elektrona bylo ne tak-to legko. Sobesednik mistera Tomtpsinsa yavno gorel
zhelaniem peredat' svoemu partneru vse poznaniya, nakoplennye za dolguyu
elektronnuyu zhizn'.
- Ne sleduet dumat', - prodolzhal elektron, - chto svyazyvanie atomov v
molekuly vsegda osushchestvlyaetsya tol'ko odnim valentnym elektronom. Sushchestvuyut
atomy, naprimer, atomy kisloroda, kotorym dlya dostraivaniya ih obolochek
neobhodimo dva elektrona, a drugim atomam dlya zapolneniya obolochek nedostaet
tri i dazhe bolee elektronov. S drugoj storony, v nekotoryh atomah yadro
uderzhivaet dva ili bolee lishnih, ili valentnyh, elektronov. Pri stolknovenii
takih atomov, mnogie elektrony pereprygivayut s odnogo atoma na drugoj, i v
rezul'tate obrazuyutsya ves'ma slozhnye molekuly, sostoyashchie iz tysyach atomov.
Sushchestvuyut takzhe tak nazyvaemye gomopolyarnye molekuly, t. e. molekuly,
sostoyashchie iz dvuh odinakovyh atomov, no eto ochen' nepriyatnaya situaciya.
- Nepriyatnaya, no pochemu? - sprosil mister Tompkins, u kotorogo vnov'
probudilsya interes k teme besedy.
- Slishkom trudno uderzhivat' ih vmeste, - poyasnil elektron. - Kak-to raz
mne prishlos' zanimat'sya etim neblagodarnym delom, i poka ya nahodilsya v
gomopolyarnoj molekule, u menya ne bylo ni sekundy pokoya. Sovsem drugoe delo v
takom atome, kak nash, kogda valentnyj elektron pereprygnul sebe i prochno
privyazal pokinutyj im atom k drugomu atomu, ispytyvavshemu elektricheskij
golod. CHtoby uderzhivat' vmeste dva odinakovyh atoma, neschastnomu elektronu
prihoditsya prygat' tuda i obratno, s odnogo atoma na drugoj i nazad, snova
na pervyj atom. CHestnoe slovo! CHuvstvuesh' sebya, kak pint-pongovyj sharik.
Mister Tompkins nemalo udivilsya, uslyshav ot elektrona, ne znavshego, chto
takoe yajco vsmyatku, stol' neprinuzhdennoe upominanie o ping-pongovom sharike,
no ne stal zadavat' voprosov.
- Ni za chto na svete ya ne soglasilsya by na takuyu rabotu opyat'! -
provorchal lenivyj elektron, podavlyaya v sebe volnu nepriyatnyh vospominanij. -
Zdes' zhe mne vpolne udobno i pokojno.
- Minutku! - voskliknul on vnezapno. - Kazhetsya, ya vizhu mestechko
poudobnee. Po-ka-a!
I gigantskim pryzhkom elektron otpravilsya kuda-to v glub' atoma.
Brosiv vzglyad v tom napravlenii, v kotorom ischez ego sobesednik, mister
Tompkins ponyal, chto proizoshlo. Odin iz nahodivshihsya na vnutrennej obolochke
elektronov byl vyrvan iz atoma kakim-to chuzhim elektronom, neozhidanno
pronikshim izvne v obolochku s vysokoj skorost'yu, i v K-obolochke obrazovalos'
uyutnoe svobodnoe mestechko. Rugaya sebya za upushchennuyu vozmozhnost'
prisoedinit'sya k elektronam vnutrennej obolochki, mister Tompkins s ogromnym
interesom nablyudal za poletom elektrona, s kotorym tol'ko chto besedoval.
Schastlivyj elektron vse glubzhe i glubzhe vnedryalsya vnutr' atoma, i yarkie luchi
sveta soprovozhdali ego triumfal'nyj polet. Lish' kogda elektron dostig
vnutrennej obolochki, eto pochti nesterpimoe siyanie prekratilos'.
- CHto eto bylo? - sprosil mister Tompkins, osleplennyj neozhidanno otkryvshimsya emu zrelishchem novogo, neizvestnogo ranee yavleniya. -
Otkuda ves' etot blesk?
- O, eto vsego lish' ispuskanie gamma-izlucheniya, svyazannoe s perehodom s
odnoj orbity na druguyu, - poyasnil partner po orbite, ulybayas' pri vide
rasteryannosti mistera Tompkinsa. - Vsyakij raz, kogda odin iz nas pronikaet
glubzhe vnutr' atoma, lishnyaya energiya nepremenno ispuskaetsya v vide izlucheniya.
|tot schastlivchik sovershil gigantskij pryzhok i ispustil pri etom ogromnuyu
energiyu. Gorazdo chashche nam prihoditsya dovol'stvovat'sya men'shimi pryzhkami na
okraine atoma, i ispuskaemoe nami izluchenie nazyvaetsya "vidimym svetom". Po
krajnej mere tak nazyvaet ego otec Paulini.
- No gamma-izluchenie, ili kak tam vy ego nazyvaete, takzhe vidimo, -
vozrazil mister Tompkins. - Mne kazhetsya, chto vasha terminologiya sposobna lish'
vvodit' v zabluzhdenie.
- Vidite li, my elektrony i chuvstvitel'ny ko vsyakogo roda izlucheniyu. No
otec Paulini rasskazyval nam o tom, chto sushchestvuyut gigantskie sushchestva, ili
kak on ih nazyval, lyudi, kotorye mogut videt' izluchenie tol'ko v uzkom
intervale energij, ili kak lyubit govorit' otec Paulini, intervale dlin voln.
V odnoj iz svoih propovedej otec Paulini upomyanul o tom, chto velikij chelovek
po imeni, kazhetsya, Rentgen otkryl gamma-izluchenie, ili rentgenovskoe
izluchenie, i teper' ono shiroko ispol'zuetsya v chem-to, chto lyudi nazyvayut
medicinoj.
- YA dovol'no horosho osvedomlen ob etom, - zametil mister Tompkins,
oshchushchaya gordost' pri mysli, chto i emu est' chto povedat' drugomu. - Hotite, ya
rasskazhu vam nemalo interesnogo ob etoj samoj medicine?
- Net, blagodaryu vas, - otvetil elektron, shiroko zevaya. - Mne kak-to
vse ravno. Razve vy ne mozhete byt' schastlivy, esli ne budete govorit' o
medicine? Dogonyajte menya!
Dovol'no dolgo mister Tompkins naslazhdalsya priyatnym oshchushcheniem svobody,
sovershaya vmeste s drugimi elektronami udivitel'nejshie perelety v
prostranstve, slovno iskusnyj akrobat, pereletayushchij s trapecii na trapeciyu.
Vnezapno on oshchutil, chto ego volosy podnyalis' dybom. Podobnoe oshchushchenie emu
prihodilos' ispytyvat' i ran'she vo vremya grozy v gorah. Misteru Tompkinsu
stalo yasno, chto k ih atomu priblizhaetsya kakoe-to sil'noe elektricheskoe
vozmushchenie, narushayushchee garmoniyu dvizheniya elektronov i zastavlyayushchee elektrony
sushchestvenno otklonyat'sya ot ih obychnyh orbit. S tochki zreniya fizika-cheloveka
vozmushchenie predstavlyalo soboj volnu ul'trafioletovogo sveta, prohodivshuyu
cherez to mesto, gde nahodilsya atom, no s tochki zreniya krohotnyh elektronov
eto byla sil'nejshaya elektricheskaya groza.
- Derzhites' pokrepche, - prokrichal misteru Tompkinsu odin iz ego
kompan'onov, - inache vas otorvut sily fotoeffekta!
No bylo slishkom pozdno. Mistera Tompkinsa otorvalo ot partnera i,
zakrutiv, s chudovishchnoj skorost'yu brosilo v prostranstvo. Oshchushchenie bylo
takoe, slovno ego shvatili ch'i-to sil'nye pal'cy. Bezdyhannyj, on unosilsya
vse dal'she i dal'she v prostranstvo, proletaya skvoz' vsyakogo roda razlichnye
atomy tak bystro, chto edva uspeval razglyadet' otdel'nye elektrony. Vnezapno
pryamo pered nim pokazalsya bol'shoj atom, i mister Tompkins ponyal, chto
stolknovenie neizbezhno.
- Proshu izvinit', no menya zafotoeffektilo i ya ne mogu... - vezhlivo
nachal mister Tompkins, no ostatok frazy potonul v oglushitel'nom treske, s
kotorym mister Tompkins vrezalsya v odin iz vneshnih elektronov. Oba uchastnika
stolknoveniya kuvyrkom poleteli v raznye storony. Odnako mister Tompkins
poteryal pri stolknovenii znachitel'nuyu chast' svoej skorosti i teper' mog
bolee detal'no obsledovat' svoe novoe okruzhenie. Gromozdivshiesya vokrug atomy
byli gorazdo bol'she teh, kotorye emu prihodilos' videt' prezhde, i v kazhdom
iz atomov mister Tompkins naschital po dvadcat' devyat' elektronov. Esli by
Tompkins luchshe razbiralsya v fizike, to on raspoznal by v nih atomy medi, no
so stol' blizkogo rasstoyaniya atomy sovsem ne pohodili na med'. Oni byli
raspolozheny vplotnuyu drug k drugu i obrazovyvali pravil'nyj uzor,
prostiravshijsya do samogo gorizonta. No bolee vsego mistera Tompkinsa udivilo
to, chto eti atomy, po-vidimomu, ne osobenno stremilis' uderzhivat' pri sebe
svoyu dolyu elektronov, v osobennosti vneshnih elektronov. Vneshnie orbity pochti
vseh atomov byli pusty, a tolpy kochuyushchih elektronov lenivo brodili po vsemu
prostranstvu, vremya ot vremeni ostanavlivayas', no nigde ne zaderzhivayas'
podolgu, na okraine to odnogo, to drugogo atoma. Utomlennyj
golovokruzhitel'nym poletom cherez prostranstvo mister Tompkins popytalsya
snachala nemnogo otdohnut' na stacionarnoj, t. e. ne podverzhennoj kakim-libo
vremennym izmeneniyam, orbite odnogo iz atomov medi, no vskore poddalsya
brodyazhnicheskim nastroeniyam tolpy i prisoedinilsya k ostal'nym elektronam v ih
bescel'nyh bluzhdaniyah.
- Poryadok zdes' ostavlyaet zhelat' luchshego, - prokommentiroval pro sebya
mister Tompkins. - Slishkom mnogo elektronov shatayutsya bez dela. YA schitayu, chto
otcu Paulini sledovalo by navesti poryadok.
- Pochemu vy dumaete, chto ya dolzhen vmeshat'sya? - razdalsya znakomyj golos
monaha, kotoryj vnezapno materializovalsya iz nichego. - Vse eti elektrony
otnyud' ne narushayut moih predpisanij i k tomu zhe delayut ochen' poleznoe delo.
Mozhet byt', vam budet nebezynteresno uznat', chto esli by vse atomy
stremilis' uderzhat' pri sebe svoi elektrony, kak eto delayut nekotorye iz
nih, to ne bylo by takogo yavleniya, kak provodimost'. U vas v dome ne bylo by
elektricheskogo dvernogo zvonka, ne govorya uzhe ob elektricheskom osveshchenii i
telefone.
- Vy hotite skazat', chto brodyachie elektrony perenosyat elektrichestvo? -
sprosil mister Tompkins, ceplyayas' za nadezhdu, chto razgovor pojdet o bolee
ili menee znakomom predmete. - No chto-to ya ne vizhu, chtoby oni dvigalis' v
kakom-to opredelennom napravlenii.
- Prezhde vsego, drug moj, - surovo promolvil monah, - ne govorite
"oni", "my" zvuchit gorazdo luchshe. Dolzhno byt', vy zabyli, chto vy sami takzhe
prinadlezhite k plemeni elektronov i chto stoit komu-nibud' nazhat' knopku
zvonka, s kotorym soedinena eta mednaya provoloka, kak elektricheskoe
napryazhenie zastavit vas vmeste s drugimi elektronami provodimosti opromet'yu
brosit'sya, chtoby vyzvat' gornichnuyu ili vypolnit' kakuyu-nibud' druguyu sluzhbu.
- No ya ne hochu delat' etogo! - tverdo zayavil mister Tompkins ne bez
razdrazheniya v golose. - I voobshche ya ustal byt' elektronom i ne vizhu v etom
bolee nichego privlekatel'nogo. CHto za zhizn' vechno vypolnyat' vse eti
elektronnye obyazannosti!
- Ne obyazatel'no vechno, - vozrazil otec Paulini, kotoromu yavno ne
ponravilos' neposlushanie so storony prostyh elektronov. - U vas vsegda est'
shans byt' unichtozhennym i prekratit' sushchestvovanie.
- B-b-byt' unichtozhennym? - povtoril mister Tompkins, chuvstvuya, kak po
spine u nego polzut murashki. - No ya vsegda dumal, chto elektrony vechny!
- Fiziki tozhe tak dumali vplot' do nedavnego vremeni, - soglasilsya otec
Paulini, yavno zabavlyayas' effektom, proizvedennym ego slovami, - no podobnaya
tochka zreniya okazalas' ne vpolne vernoj. |lektrony mogut rozhdat'sya i
umirat', kak lyudi. Razumeetsya, elektron ne mozhet umeret' ot starosti, ona
nastupaet pri stolknoveniyah.
- No ya perezhil stolknovenie lish' nedavno, i, dolzhen vam skazat',
pretyazheloe eto bylo stolknovenie, - skazal mister Tompkins, vnov' obretaya
nekotoruyu uverennost'. - Esli i takoe stolknovenie ne vyvelo menya iz stroya,
to kakim zhe ono dolzhno byt', chtoby unichtozhit' menya?
- Vopros ne v tom, kak sil'no vy stalkivaetes', - popravil mistera
Tompkinsa otec Paulini, - a v tom, s kem vy stalkivaetes'. V svoem nedavnem
stolknovenii vy, veroyatno, naskochili na drugoj otricatel'no zaryazhennyj
elektron, ochen' pohozhij na vas. Takie stolknoveniya ne tayat v sebe nikakoj
opasnosti. Vy, elektrony, mozhete stalkivat'sya drug s drugom skol'ko ugodno,
kak dva barana, eto ne prichinit nikomu iz vas ni malejshego vreda. No
sushchestvuet drugaya raznovidnost' elektronov - polozhitel'nye elektrony, lish'
sravnitel'no nedavno otkrytye fizikami. |ti polozhitel'no zaryazhennye
elektrony, ili pozitrony, vyglyadyat v tochnosti tak zhe, kak vy, s tem lish'
otlichiem, chto ih elektricheskij zaryad polozhitelen, togda kak vash otricatelen.
Pri vide priblizhayushchegosya k vam pozitrona vy polagaete, chto pered vami odin
iz nevinnyh vashih soplemennikov i ustremlyaetes' navstrechu, chtoby
privetstvovat' ego. No tut vy vnezapno oshchushchaete, chto vstrechnyj elektron ne
ottalkivaet vas slegka, chtoby izbezhat' stolknoveniya, kak eto sdelal by lyuboj
normal'nyj elektron, a prityagivaet vas k sebe i togda sdelat' chto-nibud'
pozdno.
- Uzhasno! - voskliknul mister Tompkins. - I skol'ko neschastnyh obychnyh
elektronov mozhet poglotit' odin pozitron?
- K schast'yu, tol'ko odnogo, poskol'ku unichtozhaya otricatel'no zaryazhennyj
elektron, pozitron gibnet i sam. Pozitrony mozhno opisat' kak chlenov kluba
samoubijc, ishchushchih partnerov po vzaimounichtozheniyu. Oni ne prichinyayut vreda
drug drugu, no stoit lish' kakomu-nibud' otricatel'no zaryazhennomu elektronu
vstretit'sya im na puti, kak shansov ucelet' u nego ochen' malo.
- K schast'yu, do sih por mne ne popadalis' eti chudovishcha, - proiznes
mister Tompkins, na kotorogo slova otca Paulini proizveli sil'noe
vpechatlenie. - Nadeyus', oni ne slishkom mnogochislenny?
- Ne slishkom. Po toj prostoj prichine, chto vsegda ishchut sebe
nepriyatnostej i pogibayut vskore posle rozhdeniya. Vprochem, podozhdite
minutochku, ya, kazhetsya, smogu pokazat' vam odin pozitron, - prodolzhal otec
Paulini posle korotkoj pauzy. - Esli vy vnimatel'no vglyadites' von v to
yadro, to uvidite, kak rozhdaetsya odin iz pozitronov.
Atom, na kotoryj ukazyval otec Paulini, preterpeval sil'noe
elektromagnitnoe vozmushchenie iz-za upavshego na nego izvne sil'nogo izlucheniya.
Vozmushchenie bylo gorazdo bolee sil'nym, chem to, kotoroe vybilo mistera
Tompkinsa iz atoma hlora, i semejstvo atomnyh elektronov, okruzhavshih yadro,
bylo rasseyano i uneseno proch', kak suhie list'ya uraganom.
- Vglyadites' vnimatel'no v yadro, - skazal otec Paulini, i, sosredotochiv
vse svoe vnimanie, mister Tompkins uvidel neobychnoe yavlenie, proishodivshee v
glubinah razrushennogo atoma. Vblizi yadra, v glubine vnutrennej elektronnoj
obolochki, dve smutnye teni postepenno obretali vse bolee otchetlivye
ochertaniya, i sekundoj pozzhe mister Tompkins uvidel dva blestyashchih, noven'kih
s igolochki elektrona, s ogromnoj skorost'yu razletayushchihsya ot mesta svoego
rozhdeniya.
- No ya vizhu dve chasticy, a ne odnu, - skazal mister Tompkins,
zahvachennyj otkryvshimsya emu zrelishchem.
- Mozhet byt', eto _ochen'_ horoshee pravilo, - vozrazil mister Tompkins,
- no v dannyj moment ya terplyu iz-za nego bol'shie neudobstva.
- Vizhu, syn moj, - ulybnulsya monah, - no vam prosto ne povezlo.
Ugorazdilo zhe vas stat' valentnym elektronom v atome s nechetnym atomnym
nomerom. Atom natriya, kotoromu vy prinadlezhite, obyazan imet' iz-za
elektricheskogo zaryada svoego yadra (toj bol'shoj temnoj massy, kotoruyu vy
vidite v centre) odinnadcat' elektronov. K velichajshemu sozhaleniyu dlya vas,
odinnadcat' - chislo nechetnoe, chto samo po sebe ne takaya uzh redkost', esli
prinyat' vo vnimanie, chto rovno polovina vseh celyh chisel nechetna i tol'ko
drugaya polovina chetna. Tak chto vam pridetsya kak poyavivshemusya poslednim po
krajnej mere kakoe-to vremya pobyt' odnomu.
- Vy hotite skazat', chto pozdnee u menya, vozmozhno, poyavitsya shans
obzavestis' partnerom? - s nadezhdoj sprosil mister Tompkins. - Naprimer,
vybit' s orbity kogo-nibud' iz elektronov-pervoposelencev?
- |to delaetsya ne tak, - vozrazil monah, grozya misteru Tomgasinsu
korotkim tolstym pal'cem, - no vsegda est' shans, chto kakoj-nibud' iz
elektronov, obrashchayushchihsya po vnutrennim orbitam, budet vybroshen vneshnim
vozmushcheniem i ostavit posle sebya ne zanyatoe mesto, ili vakansiyu. No na vashem
meste ya ne stal by na eto osobenno rasschityvat'.
- |lektrony skazali mne, chto bylo by luchshe, esli by ya pronik v atom
hlora, - skazal mister Tompkins, neskol'ko obeskurazhennyj slovami otca
Paulini. - Mozhete li vy posovetovat' mne, kak eto luchshe sdelat'?
- Molodoj chelovek, molodoj chelovek! - s sozhaleniem pokachal golovoj
monah. - Nu chto vam tak ne terpitsya najti kompan'ona? Pochemu vy ne mozhete po
dostoinstvu ocenit' prelest' odinochestva i nasladit'sya etoj nisposlannoj
nebom vozmozhnost'yu sozercat' s mirom sobstvennuyu dushu? Pochemu chetnye
elektrony tak sil'no l'nut k mirskoj zhizni? No esli vy nastaivaete na
priobretenii kompan'ona, ya pomogu vam osushchestvit' vashe zhelanie. Vzglyanuv v
tom napravlenii, kuda ya ukazyvayu, vy uvidite priblizhayushchijsya k nam atom
hlora, i dazhe so stol' bol'shogo rasstoyaniya vy mozhete legko razlichit'
svobodnoe mesto, gde vas, nesomnenno, ozhidaet samyj teplyj priem. |to
svobodnoe mesto nahoditsya vo vneshnej gruppe elektronov, tak nazyvaemoj
M-obolochke, kotoraya sostoit iz vos'mi elektronov, razbityh na chetyre pary.
No, kak vy vidite, chetyre elektrona vrashchayutsya vokrug svoih osej v odnom
napravlenii i tol'ko tri - v drugom, poetomu odno mesto ostaetsya vakantnym.
Vnutrennie obolochki, nazyvaemye K- i Z-obolochkami, polnost'yu zapolneny, i
atom budet rad zapoluchit' vas i zapolnit' svoyu vneshnyuyu obolochku. Kak tol'ko
dva atoma sblizyatsya, vy dolzhny prosto pereprygnut' s odnogo atoma na drugoj,
kak eto obychno delayut valentnye elektrony. Da budet mir s vami, syn moj!
S etimi slovami vnushitel'naya figura elektronnogo pastyrya vnezapno
rastvorilas' v razrezhennom vozduhe.
Obodrennyj mister Tompkins sobralsya s silami i sovershil golovolomnyj
pryzhok na orbitu proletavshego mimo atoma hlora. K svoemu udivleniyu, on
prizemlilsya na atome hlora ne bez izyashchestva i srazu zhe okazalsya v druzheskom
okruzhenii elektronov M-obolochki atoma hlora.
- Dobro pozhalovat'! Rady, chto vy prisoedinilis' k nam! - obratilsya k
nemu novyj partner s protivopolozhnym spinom, izyashchno skol'zya vdol' orbity. -
Teper' nikto ne mozhet skazat', chto nashe soobshchestvo nepolno. Teper' my mozhem
velikolepno poveselit'sya vse vmeste!
Mister Tompkins ne mog ne soglasit'sya, chto bylo dejstvitel'no veselo
(vesel'e bilo cherez kraj!), no tut emu v golovu zakralas' odna bespokojnaya
mysl'. - A kak ya ob座asnyu vse eto Mod, kogda snova uvizhu ee?
Vprochem, chuvstvo viny u mistera Tompkinsa vskore rasseyalos'.
- Mod vryad li stala by vozrazhat', - reshil on, - ved' v konce koncov eto
lish' elektrony.
- Pochemu pokinutyj vami atom ne uletaet proch'? - sprosil u mistera
Tompkinsa s nedovol'noj grimasoj ego kompan'on. - On vse eshche nadeetsya na
vashe vozvrashchenie?
Dejstvitel'no, poteryav svoj valentnyj elektron, atom natriya _nakrepko_
prilepilsya k atomu hlora, kak by v nadezhde, chto mister Tompkins peredumaet i
snova vernetsya na svoyu orbitu, po kotoroj on mchalsya v polnom odinochestve.
- Net, kak vam eto nravitsya! - serdito probormotal mister Tompkins,
hmuro glyadya na atom, kotoryj ponachalu prinyal ego tak holodno. - Ne atom, a
kakaya-to sobaka na sene!
- O, oni vsegda vedut sebya tak, eti atomy s nechetnymi nomerami, -
zametil bolee opytnyj chlen M-obolochki. - Naskol'ko ya ponimayu, vashego
vozvrashcheniya zhazhdet ne stol'ko soobshchestvo elektronov atoma natriya, skol'ko
samo yadro etogo atoma. Mezhdu central'nym yadrom i ego elektronnym eskortom
vsegda sushchestvuyut nekotorye raznoglasiya. YAdro hochet imet' vokrug sebya
stol'ko elektronov, skol'ko ono mozhet uderzhat' svoim elektricheskim zaryadom,
v to vremya kak sami elektrony predpochitayut byt' v takom kolichestve, kotoroe
pozvolyaet im do konca zapolnyat' obolochki. Sushchestvuet lish' neskol'ko vidov
atomov, tak nazyvaemye _redkie gazy_, ili, kak nazyvayut ih nemeckie fiziki,
_blagorodnye gazy_, v kotoryh zhazhda vlasti so storony atomnogo yadra i
stremleniya poddannyh-elektronov nahodyatsya v polnoj garmonii. Naprimer, takie
atomy, kak gelij, neon i argon ochen' dovol'ny caryashchim v nih soglasiem mezhdu
yadrom i elektronami i nikogda ne izgonyayut svoih elektronov i ne priglashayut
novyh. Oni himicheski inertny i derzhatsya v storone ot vseh ostal'nyh atomov.
No vo vseh ostal'nyh atomah elektronnye soobshchestva vsegda gotovy obmenyat'sya
svoimi chlenami. V atome natriya, vashem prezhnem obitalishche, svita yadra
naschityvaet na odin elektron bol'she, chem neobhodimo dlya garmonii v
obolochkah. S drugoj storony, v nashem atome normal'naya chislennost'
elektronnogo naseleniya nedostatochna dlya polnoj garmonii, poetomu my ochen'
rady vashemu pribytiyu, nesmotrya na to, chto vashe prisutstvie peregruzhaet nashe
yadro. No pokuda vy ostaetes' s nami, nash atom perestaet byt' nejtral'nym i
poluchaet dopolnitel'nyj elektricheskij zaryad. Poetomu atom natriya, kotoryj vy
pokinuli, prilip k nashemu atomu, uderzhivaemyj siloj elektricheskogo
prityazheniya. Odnazhdy mne dovelos' slyshat' nashego pervosvyashchennika otca
Paulini, i on skazal, chto atomnye soobshchestva s lishnimi ili nedostayushchimi
elektronami nazyvayutsya sootvetstvenno otricatel'nymi i polozhitel'nymi
_ionami_. Otec Paulini ispol'zoval takzhe termin molekula dlya oboznacheniya
grupp iz dvuh ili bolee atomov, uderzhivaemyh vmeste elektricheskoj siloj. V
chastnosti, kombinaciyu iz odnogo atoma natriya i odnogo atoma hlora otec
Paulini nazval molekuloj _povarennoj soli_, hotya ya reshitel'no ne ponimayu,
chto by eto moglo oznachat'.
- Vy hotite skazat', budto ne znaete, chto takoe povarennaya sol'? -
udivlenno sprosil mister Tompkins, zabyv o tom, s kem on razgovarivaet. -
|to tot samyj belyj poroshok, kotorym vy za zavtrakom posypaete yajco vsmyatku.
- A chto takoe yajco vsmyatku i chto takoe zavtrak? - s interesom sprosil
elektron.
Mister Tompkins probormotal chto-to nevnyatnoe i tut tol'ko so vsej
yasnost'yu ponyal vsyu tshchetnost' lyubyh popytok ob座asnit' svoim kompan'onam dazhe
samye nezamyslovatye detali povsednevnoj zhizni lyudej.
- Pochemu-to mne ne udaetsya pocherpnut' dlya sebya nichego novogo iz vseh
etih razgovorov o valentnosti i zapolnennyh obolochkah, - skazal sebe mister
Tompkins, reshiv naslazhdat'sya svoim vizitom v fantasticheskij mir atoma i ne
zabivat' sebe golovu neponyatnymi voprosami. No otdelat'sya ot razgovorchivogo
elektrona bylo ne tak-to legko. Sobesednik mistera Tomtpsinsa yavno gorel
zhelaniem peredat' svoemu partneru vse poznaniya, nakoplennye za dolguyu
elektronnuyu zhizn'.
- Ne sleduet dumat', - prodolzhal elektron, - chto svyazyvanie atomov v
molekuly vsegda osushchestvlyaetsya tol'ko odnim valentnym elektronom. Sushchestvuyut
atomy, naprimer, atomy kisloroda, kotorym dlya dostraivaniya ih obolochek
neobhodimo dva elektrona, a drugim atomam dlya zapolneniya obolochek nedostaet
tri i dazhe bolee elektronov. S drugoj storony, v nekotoryh atomah yadro
uderzhivaet dva ili bolee lishnih, ili valentnyh, elektronov. Pri stolknovenii
takih atomov, mnogie elektrony pereprygivayut s odnogo atoma na drugoj, i v
rezul'tate obrazuyutsya ves'ma slozhnye molekuly, sostoyashchie iz tysyach atomov.
Sushchestvuyut takzhe tak nazyvaemye gomopolyarnye molekuly, t. e. molekuly,
sostoyashchie iz dvuh odinakovyh atomov, no eto ochen' nepriyatnaya situaciya.
- Nepriyatnaya, no pochemu? - sprosil mister Tompkins, u kotorogo vnov'
probudilsya interes k teme besedy.
- Slishkom trudno uderzhivat' ih vmeste, - poyasnil elektron. - Kak-to raz
mne prishlos' zanimat'sya etim neblagodarnym delom, i poka ya nahodilsya v
gomopolyarnoj molekule, u menya ne bylo ni sekundy pokoya. Sovsem drugoe delo v
takom atome, kak nash, kogda valentnyj elektron pereprygnul sebe i prochno
privyazal pokinutyj im atom k drugomu atomu, ispytyvavshemu elektricheskij
golod. CHtoby uderzhivat' vmeste dva odinakovyh atoma, neschastnomu elektronu
prihoditsya prygat' tuda i obratno, s odnogo atoma na drugoj i nazad, snova
na pervyj atom. CHestnoe slovo! CHuvstvuesh' sebya, kak pint-pongovyj sharik.
Mister Tompkins nemalo udivilsya, uslyshav ot elektrona, ne znavshego, chto
takoe yajco vsmyatku, stol' neprinuzhdennoe upominanie o ping-pongovom sharike,
no ne stal zadavat' voprosov.
- Ni za chto na svete ya ne soglasilsya by na takuyu rabotu opyat'! -
provorchal lenivyj elektron, podavlyaya v sebe volnu nepriyatnyh vospominanij. -
Zdes' zhe mne vpolne udobno i pokojno.
- Minutku! - voskliknul on vnezapno. - Kazhetsya, ya vizhu mestechko
poudobnee. Po-ka-a!
I gigantskim pryzhkom elektron otpravilsya kuda-to v glub' atoma.
Brosiv vzglyad v tom napravlenii, v kotorom ischez ego sobesednik, mister
Tompkins ponyal, chto proizoshlo. Odin iz nahodivshihsya na vnutrennej obolochke
elektronov byl vyrvan iz atoma kakim-to chuzhim elektronom, neozhidanno
pronikshim izvne v obolochku s vysokoj skorost'yu, i v K-obolochke obrazovalos'
uyutnoe svobodnoe mestechko. Rugaya sebya za upushchennuyu vozmozhnost'
prisoedinit'sya k elektronam vnutrennej obolochki, mister Tompkins s ogromnym
interesom nablyudal za poletom elektrona, s kotorym tol'ko chto besedoval.
Schastlivyj elektron vse glubzhe i glubzhe vnedryalsya vnutr' atoma, i yarkie luchi
sveta soprovozhdali ego triumfal'nyj polet. Lish' kogda elektron dostig
vnutrennej obolochki, eto pochti nesterpimoe siyanie prekratilos'.
- CHto eto bylo? - sprosil mister Tompkins, osleplennyj neozhidanno otkryvshimsya emu zrelishchem novogo, neizvestnogo ranee yavleniya. -
Otkuda ves' etot blesk?
- O, eto vsego lish' ispuskanie gamma-izlucheniya, svyazannoe s perehodom s
odnoj orbity na druguyu, - poyasnil partner po orbite, ulybayas' pri vide
rasteryannosti mistera Tompkinsa. - Vsyakij raz, kogda odin iz nas pronikaet
glubzhe vnutr' atoma, lishnyaya energiya nepremenno ispuskaetsya v vide izlucheniya.
|tot schastlivchik sovershil gigantskij pryzhok i ispustil pri etom ogromnuyu
energiyu. Gorazdo chashche nam prihoditsya dovol'stvovat'sya men'shimi pryzhkami na
okraine atoma, i ispuskaemoe nami izluchenie nazyvaetsya "vidimym svetom". Po
krajnej mere tak nazyvaet ego otec Paulini.
- No gamma-izluchenie, ili kak tam vy ego nazyvaete, takzhe vidimo, -
vozrazil mister Tompkins. - Mne kazhetsya, chto vasha terminologiya sposobna lish'
vvodit' v zabluzhdenie.
- Vidite li, my elektrony i chuvstvitel'ny ko vsyakogo roda izlucheniyu. No
otec Paulini rasskazyval nam o tom, chto sushchestvuyut gigantskie sushchestva, ili
kak on ih nazyval, lyudi, kotorye mogut videt' izluchenie tol'ko v uzkom
intervale energij, ili kak lyubit govorit' otec Paulini, intervale dlin voln.
V odnoj iz svoih propovedej otec Paulini upomyanul o tom, chto velikij chelovek
po imeni, kazhetsya, Rentgen otkryl gamma-izluchenie, ili rentgenovskoe
izluchenie, i teper' ono shiroko ispol'zuetsya v chem-to, chto lyudi nazyvayut
medicinoj.
- YA dovol'no horosho osvedomlen ob etom, - zametil mister Tompkins,
oshchushchaya gordost' pri mysli, chto i emu est' chto povedat' drugomu. - Hotite, ya
rasskazhu vam nemalo interesnogo ob etoj samoj medicine?
- Net, blagodaryu vas, - otvetil elektron, shiroko zevaya. - Mne kak-to
vse ravno. Razve vy ne mozhete byt' schastlivy, esli ne budete govorit' o
medicine? Dogonyajte menya!
Dovol'no dolgo mister Tompkins naslazhdalsya priyatnym oshchushcheniem svobody,
sovershaya vmeste s drugimi elektronami udivitel'nejshie perelety v
prostranstve, slovno iskusnyj akrobat, pereletayushchij s trapecii na trapeciyu.
Vnezapno on oshchutil, chto ego volosy podnyalis' dybom. Podobnoe oshchushchenie emu
prihodilos' ispytyvat' i ran'she vo vremya grozy v gorah. Misteru Tompkinsu
stalo yasno, chto k ih atomu priblizhaetsya kakoe-to sil'noe elektricheskoe
vozmushchenie, narushayushchee garmoniyu dvizheniya elektronov i zastavlyayushchee elektrony
sushchestvenno otklonyat'sya ot ih obychnyh orbit. S tochki zreniya fizika-cheloveka
vozmushchenie predstavlyalo soboj volnu ul'trafioletovogo sveta, prohodivshuyu
cherez to mesto, gde nahodilsya atom, no s tochki zreniya krohotnyh elektronov
eto byla sil'nejshaya elektricheskaya groza.
- Derzhites' pokrepche, - prokrichal misteru Tompkinsu odin iz ego
kompan'onov, - inache vas otorvut sily fotoeffekta!
No bylo slishkom pozdno. Mistera Tompkinsa otorvalo ot partnera i,
zakrutiv, s chudovishchnoj skorost'yu brosilo v prostranstvo. Oshchushchenie bylo
takoe, slovno ego shvatili ch'i-to sil'nye pal'cy. Bezdyhannyj, on unosilsya
vse dal'she i dal'she v prostranstvo, proletaya skvoz' vsyakogo roda razlichnye
atomy tak bystro, chto edva uspeval razglyadet' otdel'nye elektrony. Vnezapno
pryamo pered nim pokazalsya bol'shoj atom, i mister Tompkins ponyal, chto
stolknovenie neizbezhno.
- Proshu izvinit', no menya zafotoeffektilo i ya ne mogu... - vezhlivo
nachal mister Tompkins, no ostatok frazy potonul v oglushitel'nom treske, s
kotorym mister Tompkins vrezalsya v odin iz vneshnih elektronov. Oba uchastnika
stolknoveniya kuvyrkom poleteli v raznye storony. Odnako mister Tompkins
poteryal pri stolknovenii znachitel'nuyu chast' svoej skorosti i teper' mog
bolee detal'no obsledovat' svoe novoe okruzhenie. Gromozdivshiesya vokrug atomy
byli gorazdo bol'she teh, kotorye emu prihodilos' videt' prezhde, i v kazhdom
iz atomov mister Tompkins naschital po dvadcat' devyat' elektronov. Esli by
Tompkins luchshe razbiralsya v fizike, to on raspoznal by v nih atomy medi, no
so stol' blizkogo rasstoyaniya atomy sovsem ne pohodili na med'. Oni byli
raspolozheny vplotnuyu drug k drugu i obrazovyvali pravil'nyj uzor,
prostiravshijsya do samogo gorizonta. No bolee vsego mistera Tompkinsa udivilo
to, chto eti atomy, po-vidimomu, ne osobenno stremilis' uderzhivat' pri sebe
svoyu dolyu elektronov, v osobennosti vneshnih elektronov. Vneshnie orbity pochti
vseh atomov byli pusty, a tolpy kochuyushchih elektronov lenivo brodili po vsemu
prostranstvu, vremya ot vremeni ostanavlivayas', no nigde ne zaderzhivayas'
podolgu, na okraine to odnogo, to drugogo atoma. Utomlennyj
golovokruzhitel'nym poletom cherez prostranstvo mister Tompkins popytalsya
snachala nemnogo otdohnut' na stacionarnoj, t. e. ne podverzhennoj kakim-libo
vremennym izmeneniyam, orbite odnogo iz atomov medi, no vskore poddalsya
brodyazhnicheskim nastroeniyam tolpy i prisoedinilsya k ostal'nym elektronam v ih
bescel'nyh bluzhdaniyah.
- Poryadok zdes' ostavlyaet zhelat' luchshego, - prokommentiroval pro sebya
mister Tompkins. - Slishkom mnogo elektronov shatayutsya bez dela. YA schitayu, chto
otcu Paulini sledovalo by navesti poryadok.
- Pochemu vy dumaete, chto ya dolzhen vmeshat'sya? - razdalsya znakomyj golos
monaha, kotoryj vnezapno materializovalsya iz nichego. - Vse eti elektrony
otnyud' ne narushayut moih predpisanij i k tomu zhe delayut ochen' poleznoe delo.
Mozhet byt', vam budet nebezynteresno uznat', chto esli by vse atomy
stremilis' uderzhat' pri sebe svoi elektrony, kak eto delayut nekotorye iz
nih, to ne bylo by takogo yavleniya, kak provodimost'. U vas v dome ne bylo by
elektricheskogo dvernogo zvonka, ne govorya uzhe ob elektricheskom osveshchenii i
telefone.
- Vy hotite skazat', chto brodyachie elektrony perenosyat elektrichestvo? -
sprosil mister Tompkins, ceplyayas' za nadezhdu, chto razgovor pojdet o bolee
ili menee znakomom predmete. - No chto-to ya ne vizhu, chtoby oni dvigalis' v
kakom-to opredelennom napravlenii.
- Prezhde vsego, drug moj, - surovo promolvil monah, - ne govorite
"oni", "my" zvuchit gorazdo luchshe. Dolzhno byt', vy zabyli, chto vy sami takzhe
prinadlezhite k plemeni elektronov i chto stoit komu-nibud' nazhat' knopku
zvonka, s kotorym soedinena eta mednaya provoloka, kak elektricheskoe
napryazhenie zastavit vas vmeste s drugimi elektronami provodimosti opromet'yu
brosit'sya, chtoby vyzvat' gornichnuyu ili vypolnit' kakuyu-nibud' druguyu sluzhbu.
- No ya ne hochu delat' etogo! - tverdo zayavil mister Tompkins ne bez
razdrazheniya v golose. - I voobshche ya ustal byt' elektronom i ne vizhu v etom
bolee nichego privlekatel'nogo. CHto za zhizn' vechno vypolnyat' vse eti
elektronnye obyazannosti!
- Ne obyazatel'no vechno, - vozrazil otec Paulini, kotoromu yavno ne
ponravilos' neposlushanie so storony prostyh elektronov. - U vas vsegda est'
shans byt' unichtozhennym i prekratit' sushchestvovanie.
- B-b-byt' unichtozhennym? - povtoril mister Tompkins, chuvstvuya, kak po
spine u nego polzut murashki. - No ya vsegda dumal, chto elektrony vechny!
- Fiziki tozhe tak dumali vplot' do nedavnego vremeni, - soglasilsya otec
Paulini, yavno zabavlyayas' effektom, proizvedennym ego slovami, - no podobnaya
tochka zreniya okazalas' ne vpolne vernoj. |lektrony mogut rozhdat'sya i
umirat', kak lyudi. Razumeetsya, elektron ne mozhet umeret' ot starosti, ona
nastupaet pri stolknoveniyah.
- No ya perezhil stolknovenie lish' nedavno, i, dolzhen vam skazat',
pretyazheloe eto bylo stolknovenie, - skazal mister Tompkins, vnov' obretaya
nekotoruyu uverennost'. - Esli i takoe stolknovenie ne vyvelo menya iz stroya,
to kakim zhe ono dolzhno byt', chtoby unichtozhit' menya?
- Vopros ne v tom, kak sil'no vy stalkivaetes', - popravil mistera
Tompkinsa otec Paulini, - a v tom, s kem vy stalkivaetes'. V svoem nedavnem
stolknovenii vy, veroyatno, naskochili na drugoj otricatel'no zaryazhennyj
elektron, ochen' pohozhij na vas. Takie stolknoveniya ne tayat v sebe nikakoj
opasnosti. Vy, elektrony, mozhete stalkivat'sya drug s drugom skol'ko ugodno,
kak dva barana, eto ne prichinit nikomu iz vas ni malejshego vreda. No
sushchestvuet drugaya raznovidnost' elektronov - polozhitel'nye elektrony, lish'
sravnitel'no nedavno otkrytye fizikami. |ti polozhitel'no zaryazhennye
elektrony, ili pozitrony, vyglyadyat v tochnosti tak zhe, kak vy, s tem lish'
otlichiem, chto ih elektricheskij zaryad polozhitelen, togda kak vash otricatelen.
Pri vide priblizhayushchegosya k vam pozitrona vy polagaete, chto pered vami odin
iz nevinnyh vashih soplemennikov i ustremlyaetes' navstrechu, chtoby
privetstvovat' ego. No tut vy vnezapno oshchushchaete, chto vstrechnyj elektron ne
ottalkivaet vas slegka, chtoby izbezhat' stolknoveniya, kak eto sdelal by lyuboj
normal'nyj elektron, a prityagivaet vas k sebe i togda sdelat' chto-nibud'
pozdno.
- Uzhasno! - voskliknul mister Tompkins. - I skol'ko neschastnyh obychnyh
elektronov mozhet poglotit' odin pozitron?
- K schast'yu, tol'ko odnogo, poskol'ku unichtozhaya otricatel'no zaryazhennyj
elektron, pozitron gibnet i sam. Pozitrony mozhno opisat' kak chlenov kluba
samoubijc, ishchushchih partnerov po vzaimounichtozheniyu. Oni ne prichinyayut vreda
drug drugu, no stoit lish' kakomu-nibud' otricatel'no zaryazhennomu elektronu
vstretit'sya im na puti, kak shansov ucelet' u nego ochen' malo.
- K schast'yu, do sih por mne ne popadalis' eti chudovishcha, - proiznes
mister Tompkins, na kotorogo slova otca Paulini proizveli sil'noe
vpechatlenie. - Nadeyus', oni ne slishkom mnogochislenny?
- Ne slishkom. Po toj prostoj prichine, chto vsegda ishchut sebe
nepriyatnostej i pogibayut vskore posle rozhdeniya. Vprochem, podozhdite
minutochku, ya, kazhetsya, smogu pokazat' vam odin pozitron, - prodolzhal otec
Paulini posle korotkoj pauzy. - Esli vy vnimatel'no vglyadites' von v to
yadro, to uvidite, kak rozhdaetsya odin iz pozitronov.
Atom, na kotoryj ukazyval otec Paulini, preterpeval sil'noe
elektromagnitnoe vozmushchenie iz-za upavshego na nego izvne sil'nogo izlucheniya.
Vozmushchenie bylo gorazdo bolee sil'nym, chem to, kotoroe vybilo mistera
Tompkinsa iz atoma hlora, i semejstvo atomnyh elektronov, okruzhavshih yadro,
bylo rasseyano i uneseno proch', kak suhie list'ya uraganom.
- Vglyadites' vnimatel'no v yadro, - skazal otec Paulini, i, sosredotochiv
vse svoe vnimanie, mister Tompkins uvidel neobychnoe yavlenie, proishodivshee v
glubinah razrushennogo atoma. Vblizi yadra, v glubine vnutrennej elektronnoj
obolochki, dve smutnye teni postepenno obretali vse bolee otchetlivye
ochertaniya, i sekundoj pozzhe mister Tompkins uvidel dva blestyashchih, noven'kih
s igolochki elektrona, s ogromnoj skorost'yu razletayushchihsya ot mesta svoego
rozhdeniya.
- No ya vizhu dve chasticy, a ne odnu, - skazal mister Tompkins,
zahvachennyj otkryvshimsya emu zrelishchem.
 - Sovershenno verno, - soglasilsya otec Paulini. - |lektrony vsegda
rozhdayutsya parami, inache rozhdenie elektronov protivorechilo by zakonu
sohraneniya elektricheskogo zaryada. Odna iz etih dvuh chastic, rodivshihsya pod
dejstviem sil'nogo gamma-izlucheniya na yadro, - obychnyj elektron s
otricatel'nym zaryadom, drugaya chastica - elektron s polozhitel'nym zaryadom,
ili pozitron-ubijca. Teper' on ryshchet po prostranstvu v poiskah zhertvy.
- Nu chto zh, - zadumchivo proiznes mister Tompkins, - esli rozhdenie
kazhdogo pozitrona, kotoromu na rodu napisano stat' ubijcej elektrona,
soprovozhdaetsya rozhdeniem odnogo obychnogo elektrona, to dela obstoyat ne tak
uzh ploho. Po krajnej mere ne prihoditsya opasat'sya za ischeznovenie
elektronnogo plemeni, i ya...
- Ostorozhno! - prerval mistera Tompkinsa otec Paulini, ottalkivaya
svoego sobesednika v storonu, v to vremya kak novorozhdennyj pozitron so
svistom pronessya v kakom-nibud' dyujme ot nih. - Nuzhno vse vremya byt' nacheku,
kogda eti ubijstvennye chasticy nahodyatsya gde-to poblizosti. No, prostite, ya
slishkom zaderzhalsya, beseduya s vami, i menya zhdut drugie dela. Mne neobhodimo
navestit' milyh moemu serdcu _nejtrino_...
I otec Paulini ischez, ostaviv mistera Tompkinsa v nevedenii
otnositel'no togo, chto takoe nejtrino i sleduet li ih opasat'sya. Lishivshis'
duhovnogo otca, mister Tompkins pochuvstvoval sebya eshche bolee odinokim, chem
prezhde, i vsyakij raz, kogda na ego dolgom puti cherez prostranstvo; k nemu
priblizhalsya tot ili inoj soplemennik-elektron, v serdce mistera Tompkinsa
nachinala teplit'sya nadezhda na to, chto pod nevinnoj vneshnost'yu mozhet
skryvat'sya serdce ubijcy. Vremya tyanulos' nesterpimo medlenno (misteru
Tompkinsu kazalos', chto proshlo neskol'ko stoletij), a ego nadezhdam i chayaniyam
vse nikak ne suzhdeno bylo sbyt'sya, i misteru Tompkinsu ne ostavalos' nichego
drugogo, kak ispolnyat' skuchnye obyazannosti elektrona provodimosti.
Vse proizoshlo sovershenno neozhidanno, kogda mister Tompkins menee vsego
rasschityval vstretit' pozitron. Oshchushchaya ostruyu potrebnost' pobesedovat' s
kem-nibud', dazhe s kakim-nibud' glupym elektronom provodimosti, on
priblizilsya k chastice, medlenno proletavshej mimo i yavno byvshej novichkom v
dannoj chasti mednoj provoloki. No dazhe na rasstoyanii mister Tompkins ponyal,
chto oshibsya v vybore sobesednika i chto neodolimaya sila prityazheniya uvlekaet
ego, ne davaya otstupit' ni na shag. Kakoj-to mig on pytalsya borot'sya i
vyryvat'sya, no rasstoyanie mezhdu nim i drugoj chasticej vse sokrashchalos', i
misteru Tompkinsu pokazalos', chto on uzhe vidit torzhestvuyushchuyu ulybku na lice
svoego protivnika.
- Pustite menya! Pustite menya nemedlenno! - zakrichal mister Tompkins vo
ves' golos, izo vseh sil otbivayas' rukami i nogami. - YA ne hochu
annigilirovat'! YA hochu vechno provodit' elektricheskij tok!
No vse bylo tshchetno, i okruzhayushchee prostranstvo vnezapno ozarilos'
oslepitel'noj vspyshkoj sil'nejshego izlucheniya.
- Itak, menya bol'she net, - podumal mister Tompkins, - no kak zhe v takom
sluchae ya mogu myslit'? Mozhet byt' annigilirovalo tol'ko moe telo, a dusha moya
uletela na kvantovye nebesa?
Tut on oshchutil novuyu silu, na etot raz dejstvovavshuyu myagche, kotoraya
tverdo i reshitel'no tryasla ego. Otkryv glaza, mister Tompkins uvidel pered
soboj universitetskogo sluzhitelya.
- Prostite, ser, - skazal tot, - no lekciya uzhe davno zakonchilas' i nam
nuzhno zakryt' auditoriyu.
Mister Tompkins s trudom podavlyal zevotu i chuvstvoval sebya ves'ma
nelovko.
- Spokojnoj nochi, ser, - pozhelal emu sluzhitel' s sochuvstvennoj ulybkoj.
Glava 10 1/2
CHast' predydushchej lekcii, kotoruyu prospal mister Tompkins
V 1908 g. anglijskij fizik Dzhon Dal'ton otkryl zakon kratnyh otnoshenij.
On pokazal, chto otnositel'nye proporcii razlichnyh himicheskih elementov,
neobhodimyh dlya obrazovaniya bolee slozhnyh himicheskih veshchestv, vsegda mogut
byt' vyrazheny kak otnosheniya celyh chisel i ob座asnil svoj zakon tem, chto vse
slozhnye himicheskie veshchestva sostoyat iz razlichnogo chisla chastic,
sootvetstvuyushchih prostym himicheskim elementam. Bezuspeshnye popytki
srednevekovoj alhimii prevratit' odin himicheskij element v drugoj sluzhat eshche
odnim dokazatel'stvom kazhushchejsya nedelimosti mel'chajshih chastic veshchestva,
kotorye bez osobyh kolebanij byli nazvany svoim drevnegrecheskim imenem -
atomy. Dannoe edinozhdy, eto nazvanie zakrepilos', i hotya teper' tverdo
ustanovleno, chto atomy Dal'tona otnyud' ne nedelimy i v dejstvitel'nosti
sostoyat iz bol'shogo chisla bolee melkih, subatomnyh chastic, obychno my
predpochitaem zakryvat' glaza na filologicheskuyu neposledovatel'nost' etogo
nazvaniya.
Itak, to, chto v sovremennoj fizike prinyato nazyvat' atomami, otnyud' ne
yavlyaetsya elementarnymi i nedelimymi sostavnymi chastyami materii, o kotoryh
govoril v svoih umozritel'nyh postroeniyah Demokrit, i termin "atom" byl by
bolee obosnovan primenitel'no k bolee melkim subatomnym chasticam, takim kak
elektrony i protony, iz kotoryh sostoyat atomy Dal'tona. No takoe izmenenie
terminologii porodilo by slishkom bol'shuyu putanicu, i ni odin fizik ne
zabotitsya osobenno o filologicheskoj neposledovatel'nosti sushchestvuyushchej nyne
terminologii. Poetomu my upotreblyaem staroe nazvanie "atomy" v tom zhe
smysle, v kakom ego upotreblyal Dal'ton, a elektrony, protony i drugie
subatomnye edinicy materii nazyvaem _elementarnymi chasticami_.
|to nazvanie svidetel'stvuet o tom, chto v nastoyashchee vremya my schitaem
eti subatomnye chasticy dejstvitel'no elementarnymi i nedelimymi v smysle
Demokrita, i vy, estestvenno, mozhete sprosit' u menya, ne povtoritsya li
istoriya i ne vyyasnitsya li v hode dal'nejshego razvitiya sovremennoj fiziki,
chto tak nazyvaemye elementarnye chasticy v dejstvitel'nosti obladayut ves'ma
slozhnoj vnutrennej strukturoj. Moj otvet sostoit v tom, chto hotya net
absolyutnoj garantii, chto nichego takogo ne proizojdet, imeyutsya dostatochno
veskie osnovaniya polagat', chto na etot raz my ne oshiblis'. Dejstvitel'no,
sushchestvuyut devyanosto dve raznovidnosti atomov (sootvetstvuyushchie devyanosto
dvum razlichnym himicheskim elementam), i kazhdyj takoj atom obladaet ves'ma
slozhnymi harakternymi svojstvami. V podobnoj situacii samo soboj
naprashivaetsya uproshchenie - stremlenie svesti slozhnuyu kartinu k bolee prostoj.
S drugoj storony, v sovremennoj fizike izvestny lish' neskol'ko razlichnyh
tipov elementarnyh chastic: _elektrony_ (otricatel'no i polozhitel'no
zaryazhennye legkie chasticy), _nuklony_ (zaryazhennye ili nejtral'nye tyazhelye
chasticy, izvestnye pod nazvaniem _protonov_ i _nejtronov_) i, vozmozhno, tak
nazyvaemye _nejtrino_, priroda kotoryh polnost'yu ne vyyasnena.
Svojstva etih elementarnyh chastic chrezvychajno prosty, i dal'nejshee
delenie materii ne privedet k skol'ko-nibud' sushchestvennomu uproshcheniyu. Krome
togo, kak vy ponimaete, vsegda neobhodimo imet' neskol'ko elementarnyh
ponyatij, s kotorymi mozhno bylo by igrat', esli vy hotite postroit' nechto
bolee slozhnoe. Dva ili tri takih elementarnyh ponyatiya - otnyud' ne mnogo. YA
schitayu, chto vy mozhete spokojno postavit' poslednij dollar, derzha pari, chto
elementarnye chasticy sovremennoj fiziki ostanutsya dostojnymi svoego
nazvaniya.
No vernemsya k voprosu o tom, kakim obrazom atomy Dal'tona postroeny iz
elementarnyh chastic. Pervyj pravil'nyj otvet na etot vopros byl dan v 1911
g. znamenitym britanskim fizikom |rnestom Rezerfordom (vposledstvii
Rezerford lord Nel'son). Rezerford issledoval stroenie atoma, bombardiruya
razlichnye atomy bystro dvizhushchimisya krohotnymi snaryadami, izvestnymi pod
nazvaniem _al'fa-chasticy_, ispuskaemymi pri raspade radioaktivnyh elementov.
Nablyudaya za otkloneniyami (rasseyaniem) snaryadov posle prohozhdeniya kusochka
materii (listochka fol'gi), Rezerford prishel k vyvodu, chto vse atomy dolzhny
obladat' ochen' plotnoj polozhitel'no zaryazhennoj serdcevinoj (atomnym yadrom),
okruzhennoj gorazdo bolee razrezhennym otricatel'no zaryazhennym oblakom
(atomnoj atmosferoj). Nyne my znaem, chto atomnoe yadro sostoit iz
opredelennogo chisla protonov i nejtronov, izvestnyh pod sobiratel'nym
nazvaniem nuklonov. Nuklony tesno svyazany mezhdu soboj sil'nymi silami
scepleniya. Atomnaya atmosfera sostoit iz razlichnogo chisla otricatel'no
zaryazhennyh elektronov, kotorye roem okruzhayut atomnoe yadro pod dejstviem
elektrostaticheskogo prityazheniya ego polozhitel'nogo zaryada. CHislo elektronov,
obrazuyushchih atomnuyu atmosferu, opredelyaet vse fizicheskie i himicheskie
svojstva atoma i izmenyaetsya vdol' estestvennoj posledovatel'nosti himicheskih
elementov ot odnogo elektrona (dlya vodoroda) do devyanosto dvuh elektronov
(dlya samogo tyazhelogo iz izvestnyh elementov urana).
Nesmotrya na kazhushchuyusya prostotu atomnoj modeli Rezerforda, ee detal'nyj
analiz okazalsya daleko ne prostym. Dejstvitel'no, soglasno odnomu iz
naibolee gluboko ukorenivshihsya predstavlenij klassicheskoj fiziki,
otricatel'no zaryazhennye elektrony, obrashchayas' vokrug atomnogo yadra, dolzhny
teryat' svoyu energiyu v vide ispuskaemogo imi izlucheniya (sveta). Kak
pokazyvayut vychisleniya, iz-za postoyannyh poter' energii vse elektrony,
obrazuyushchie atomnuyu atmosferu, dolzhny byli by za nichtozhno maluyu dolyu sekundy
upast' na yadro. |to, kazalos' by, vpolne zdravoe rassuzhdenie klassicheskoj
teorii nahoditsya v rezkom protivorechii s tem empiricheskim faktom, chto
atomnye atmosfery ochen' stabil'ny i atomnye elektrony ne padayut na yadro, a
beskonechno dolgo kruzhatsya roem vokrug central'nogo tela. Takim obrazom,
mezhdu osnovnymi predstavleniyami klassicheskoj mehaniki i empiricheskimi
dannymi otnositel'no mehanicheskogo povedeniya krohotnyh sostavnyh chastej mira
atomov voznikaet glubokoe protivorechie. Razmyshleniya nad etim protivorechiem
priveli izvestnogo datskogo fizika Nil'sa Bora k zaklyucheniyu, chto
klassicheskaya mehanika, na protyazhenii stoletij pretendovavshaya na osoboe
nezyblemoe polozhenie v sisteme estestvennyh nauk, dolzhna otnyne
rassmatrivat'sya kak ogranichennaya teoriya, primenimaya k makroskopicheskomu miru
povsednevnogo opyta, no utrachivayushchaya silu pri popytke primenit' ee k gorazdo
bolee tonkim tipam dvizheniya proishodyashchego vnutri razlichnyh atomov. V
kachestve probnogo fundamenta novoj obobshchennoj mehaniki, primenimoj i k
dvizheniyu krohotnyh podvizhnyh chastej atomnogo mehanizma, Bor predlozhil
gipotezu o tom, chto _iz vsego beskonechnogo raznoobraziya tipov dvizheniya,
rassmatrivaemyh v klassicheskoj mehanike, v prirode realizuetsya tol'ko
neskol'ko special'no vybrannyh tipov_. |ti razreshennye tipy dvizheniya
(nazyvaemye takzhe razreshennymi traektoriyami, ili orbitami) otbirayutsya v
sootvetstvii s opredelennymi matematicheskimi usloviyami, izvestnymi pod
nazvaniem _uslovij kvantovaniya_ v teorii Bora. YA ne stanu vhodit' zdes' v
podrobnoe obsuzhdenie etih uslovij kvantovaniya, no hochu lish' upomyanut' ob
odnom obstoyatel'stve: vse eti usloviya vybrany takim obrazom, chto nalagaemye
imi ogranicheniya ne imeyut prakticheskogo znacheniya v teh sluchayah, kogda massa
dvizhushchejsya chasticy vo mnogo raz bol'she mass, s kotorymi my vstrechaemsya v
strukture atoma. Sledovatel'no, primenitel'no k makroskopicheskim telam novaya
_mikromehanika_ privodit k tem zhe rezul'tatam, chto i staraya klassicheskaya
teoriya (_princip sootvetstviya_) i tol'ko pri perehode k mikroskopicheskim
atomnym mehanizmam raznoglasiya mezhdu staroj i novoj teoriyami stanovyatsya
sushchestvennymi. Ne vdavayas' v detali, ya hochu udovletvorit' vashe lyubopytstvo i
prodemonstrirovat' stroenie atoma s tochki zreniya teorii Bora, a imenno shemu
raspolozheniya kvantovyh orbit v atome po Boru (pervyj slajd, pozhalujsta!). Vy
vidite (sm. ris. na s. 163), razumeetsya, v sil'no uvelichennom masshtabe,
sistemu krugovyh i ellipticheskih orbit. Oni predstavlyayut edinstvenno
"razreshennye" usloviyami kvantovaniya Bora tipy dvizhenij dlya elektronov,
obrazuyushchih atomnuyu atmosferu. V to vremya kak klassicheskaya mehanika razreshaet
elektronu dvigat'sya _na lyubom_ rasstoyanii ot yadra i ne nakladyvaet
ogranichenij na ekscentrisitet (t. e. na udlinenie, ili vytyanutost') orbity,
razreshennye orbity v teorii Bora obrazuyut diskretnoe mnozhestvo s vpolne
opredelennymi harakternymi razmerami. CHisla i latinskie bukvy, stoyashchie u
kazhdoj orbity, ukazyvayut nazvanie sootvetstvuyushchej orbity v obshchej
klassifikacii. Vy mozhete, naprimer, zametit', chto bol'shie chisla
sootvetstvuyut orbitam s bol'shimi diametrami.
- Sovershenno verno, - soglasilsya otec Paulini. - |lektrony vsegda
rozhdayutsya parami, inache rozhdenie elektronov protivorechilo by zakonu
sohraneniya elektricheskogo zaryada. Odna iz etih dvuh chastic, rodivshihsya pod
dejstviem sil'nogo gamma-izlucheniya na yadro, - obychnyj elektron s
otricatel'nym zaryadom, drugaya chastica - elektron s polozhitel'nym zaryadom,
ili pozitron-ubijca. Teper' on ryshchet po prostranstvu v poiskah zhertvy.
- Nu chto zh, - zadumchivo proiznes mister Tompkins, - esli rozhdenie
kazhdogo pozitrona, kotoromu na rodu napisano stat' ubijcej elektrona,
soprovozhdaetsya rozhdeniem odnogo obychnogo elektrona, to dela obstoyat ne tak
uzh ploho. Po krajnej mere ne prihoditsya opasat'sya za ischeznovenie
elektronnogo plemeni, i ya...
- Ostorozhno! - prerval mistera Tompkinsa otec Paulini, ottalkivaya
svoego sobesednika v storonu, v to vremya kak novorozhdennyj pozitron so
svistom pronessya v kakom-nibud' dyujme ot nih. - Nuzhno vse vremya byt' nacheku,
kogda eti ubijstvennye chasticy nahodyatsya gde-to poblizosti. No, prostite, ya
slishkom zaderzhalsya, beseduya s vami, i menya zhdut drugie dela. Mne neobhodimo
navestit' milyh moemu serdcu _nejtrino_...
I otec Paulini ischez, ostaviv mistera Tompkinsa v nevedenii
otnositel'no togo, chto takoe nejtrino i sleduet li ih opasat'sya. Lishivshis'
duhovnogo otca, mister Tompkins pochuvstvoval sebya eshche bolee odinokim, chem
prezhde, i vsyakij raz, kogda na ego dolgom puti cherez prostranstvo; k nemu
priblizhalsya tot ili inoj soplemennik-elektron, v serdce mistera Tompkinsa
nachinala teplit'sya nadezhda na to, chto pod nevinnoj vneshnost'yu mozhet
skryvat'sya serdce ubijcy. Vremya tyanulos' nesterpimo medlenno (misteru
Tompkinsu kazalos', chto proshlo neskol'ko stoletij), a ego nadezhdam i chayaniyam
vse nikak ne suzhdeno bylo sbyt'sya, i misteru Tompkinsu ne ostavalos' nichego
drugogo, kak ispolnyat' skuchnye obyazannosti elektrona provodimosti.
Vse proizoshlo sovershenno neozhidanno, kogda mister Tompkins menee vsego
rasschityval vstretit' pozitron. Oshchushchaya ostruyu potrebnost' pobesedovat' s
kem-nibud', dazhe s kakim-nibud' glupym elektronom provodimosti, on
priblizilsya k chastice, medlenno proletavshej mimo i yavno byvshej novichkom v
dannoj chasti mednoj provoloki. No dazhe na rasstoyanii mister Tompkins ponyal,
chto oshibsya v vybore sobesednika i chto neodolimaya sila prityazheniya uvlekaet
ego, ne davaya otstupit' ni na shag. Kakoj-to mig on pytalsya borot'sya i
vyryvat'sya, no rasstoyanie mezhdu nim i drugoj chasticej vse sokrashchalos', i
misteru Tompkinsu pokazalos', chto on uzhe vidit torzhestvuyushchuyu ulybku na lice
svoego protivnika.
- Pustite menya! Pustite menya nemedlenno! - zakrichal mister Tompkins vo
ves' golos, izo vseh sil otbivayas' rukami i nogami. - YA ne hochu
annigilirovat'! YA hochu vechno provodit' elektricheskij tok!
No vse bylo tshchetno, i okruzhayushchee prostranstvo vnezapno ozarilos'
oslepitel'noj vspyshkoj sil'nejshego izlucheniya.
- Itak, menya bol'she net, - podumal mister Tompkins, - no kak zhe v takom
sluchae ya mogu myslit'? Mozhet byt' annigilirovalo tol'ko moe telo, a dusha moya
uletela na kvantovye nebesa?
Tut on oshchutil novuyu silu, na etot raz dejstvovavshuyu myagche, kotoraya
tverdo i reshitel'no tryasla ego. Otkryv glaza, mister Tompkins uvidel pered
soboj universitetskogo sluzhitelya.
- Prostite, ser, - skazal tot, - no lekciya uzhe davno zakonchilas' i nam
nuzhno zakryt' auditoriyu.
Mister Tompkins s trudom podavlyal zevotu i chuvstvoval sebya ves'ma
nelovko.
- Spokojnoj nochi, ser, - pozhelal emu sluzhitel' s sochuvstvennoj ulybkoj.
Glava 10 1/2
CHast' predydushchej lekcii, kotoruyu prospal mister Tompkins
V 1908 g. anglijskij fizik Dzhon Dal'ton otkryl zakon kratnyh otnoshenij.
On pokazal, chto otnositel'nye proporcii razlichnyh himicheskih elementov,
neobhodimyh dlya obrazovaniya bolee slozhnyh himicheskih veshchestv, vsegda mogut
byt' vyrazheny kak otnosheniya celyh chisel i ob座asnil svoj zakon tem, chto vse
slozhnye himicheskie veshchestva sostoyat iz razlichnogo chisla chastic,
sootvetstvuyushchih prostym himicheskim elementam. Bezuspeshnye popytki
srednevekovoj alhimii prevratit' odin himicheskij element v drugoj sluzhat eshche
odnim dokazatel'stvom kazhushchejsya nedelimosti mel'chajshih chastic veshchestva,
kotorye bez osobyh kolebanij byli nazvany svoim drevnegrecheskim imenem -
atomy. Dannoe edinozhdy, eto nazvanie zakrepilos', i hotya teper' tverdo
ustanovleno, chto atomy Dal'tona otnyud' ne nedelimy i v dejstvitel'nosti
sostoyat iz bol'shogo chisla bolee melkih, subatomnyh chastic, obychno my
predpochitaem zakryvat' glaza na filologicheskuyu neposledovatel'nost' etogo
nazvaniya.
Itak, to, chto v sovremennoj fizike prinyato nazyvat' atomami, otnyud' ne
yavlyaetsya elementarnymi i nedelimymi sostavnymi chastyami materii, o kotoryh
govoril v svoih umozritel'nyh postroeniyah Demokrit, i termin "atom" byl by
bolee obosnovan primenitel'no k bolee melkim subatomnym chasticam, takim kak
elektrony i protony, iz kotoryh sostoyat atomy Dal'tona. No takoe izmenenie
terminologii porodilo by slishkom bol'shuyu putanicu, i ni odin fizik ne
zabotitsya osobenno o filologicheskoj neposledovatel'nosti sushchestvuyushchej nyne
terminologii. Poetomu my upotreblyaem staroe nazvanie "atomy" v tom zhe
smysle, v kakom ego upotreblyal Dal'ton, a elektrony, protony i drugie
subatomnye edinicy materii nazyvaem _elementarnymi chasticami_.
|to nazvanie svidetel'stvuet o tom, chto v nastoyashchee vremya my schitaem
eti subatomnye chasticy dejstvitel'no elementarnymi i nedelimymi v smysle
Demokrita, i vy, estestvenno, mozhete sprosit' u menya, ne povtoritsya li
istoriya i ne vyyasnitsya li v hode dal'nejshego razvitiya sovremennoj fiziki,
chto tak nazyvaemye elementarnye chasticy v dejstvitel'nosti obladayut ves'ma
slozhnoj vnutrennej strukturoj. Moj otvet sostoit v tom, chto hotya net
absolyutnoj garantii, chto nichego takogo ne proizojdet, imeyutsya dostatochno
veskie osnovaniya polagat', chto na etot raz my ne oshiblis'. Dejstvitel'no,
sushchestvuyut devyanosto dve raznovidnosti atomov (sootvetstvuyushchie devyanosto
dvum razlichnym himicheskim elementam), i kazhdyj takoj atom obladaet ves'ma
slozhnymi harakternymi svojstvami. V podobnoj situacii samo soboj
naprashivaetsya uproshchenie - stremlenie svesti slozhnuyu kartinu k bolee prostoj.
S drugoj storony, v sovremennoj fizike izvestny lish' neskol'ko razlichnyh
tipov elementarnyh chastic: _elektrony_ (otricatel'no i polozhitel'no
zaryazhennye legkie chasticy), _nuklony_ (zaryazhennye ili nejtral'nye tyazhelye
chasticy, izvestnye pod nazvaniem _protonov_ i _nejtronov_) i, vozmozhno, tak
nazyvaemye _nejtrino_, priroda kotoryh polnost'yu ne vyyasnena.
Svojstva etih elementarnyh chastic chrezvychajno prosty, i dal'nejshee
delenie materii ne privedet k skol'ko-nibud' sushchestvennomu uproshcheniyu. Krome
togo, kak vy ponimaete, vsegda neobhodimo imet' neskol'ko elementarnyh
ponyatij, s kotorymi mozhno bylo by igrat', esli vy hotite postroit' nechto
bolee slozhnoe. Dva ili tri takih elementarnyh ponyatiya - otnyud' ne mnogo. YA
schitayu, chto vy mozhete spokojno postavit' poslednij dollar, derzha pari, chto
elementarnye chasticy sovremennoj fiziki ostanutsya dostojnymi svoego
nazvaniya.
No vernemsya k voprosu o tom, kakim obrazom atomy Dal'tona postroeny iz
elementarnyh chastic. Pervyj pravil'nyj otvet na etot vopros byl dan v 1911
g. znamenitym britanskim fizikom |rnestom Rezerfordom (vposledstvii
Rezerford lord Nel'son). Rezerford issledoval stroenie atoma, bombardiruya
razlichnye atomy bystro dvizhushchimisya krohotnymi snaryadami, izvestnymi pod
nazvaniem _al'fa-chasticy_, ispuskaemymi pri raspade radioaktivnyh elementov.
Nablyudaya za otkloneniyami (rasseyaniem) snaryadov posle prohozhdeniya kusochka
materii (listochka fol'gi), Rezerford prishel k vyvodu, chto vse atomy dolzhny
obladat' ochen' plotnoj polozhitel'no zaryazhennoj serdcevinoj (atomnym yadrom),
okruzhennoj gorazdo bolee razrezhennym otricatel'no zaryazhennym oblakom
(atomnoj atmosferoj). Nyne my znaem, chto atomnoe yadro sostoit iz
opredelennogo chisla protonov i nejtronov, izvestnyh pod sobiratel'nym
nazvaniem nuklonov. Nuklony tesno svyazany mezhdu soboj sil'nymi silami
scepleniya. Atomnaya atmosfera sostoit iz razlichnogo chisla otricatel'no
zaryazhennyh elektronov, kotorye roem okruzhayut atomnoe yadro pod dejstviem
elektrostaticheskogo prityazheniya ego polozhitel'nogo zaryada. CHislo elektronov,
obrazuyushchih atomnuyu atmosferu, opredelyaet vse fizicheskie i himicheskie
svojstva atoma i izmenyaetsya vdol' estestvennoj posledovatel'nosti himicheskih
elementov ot odnogo elektrona (dlya vodoroda) do devyanosto dvuh elektronov
(dlya samogo tyazhelogo iz izvestnyh elementov urana).
Nesmotrya na kazhushchuyusya prostotu atomnoj modeli Rezerforda, ee detal'nyj
analiz okazalsya daleko ne prostym. Dejstvitel'no, soglasno odnomu iz
naibolee gluboko ukorenivshihsya predstavlenij klassicheskoj fiziki,
otricatel'no zaryazhennye elektrony, obrashchayas' vokrug atomnogo yadra, dolzhny
teryat' svoyu energiyu v vide ispuskaemogo imi izlucheniya (sveta). Kak
pokazyvayut vychisleniya, iz-za postoyannyh poter' energii vse elektrony,
obrazuyushchie atomnuyu atmosferu, dolzhny byli by za nichtozhno maluyu dolyu sekundy
upast' na yadro. |to, kazalos' by, vpolne zdravoe rassuzhdenie klassicheskoj
teorii nahoditsya v rezkom protivorechii s tem empiricheskim faktom, chto
atomnye atmosfery ochen' stabil'ny i atomnye elektrony ne padayut na yadro, a
beskonechno dolgo kruzhatsya roem vokrug central'nogo tela. Takim obrazom,
mezhdu osnovnymi predstavleniyami klassicheskoj mehaniki i empiricheskimi
dannymi otnositel'no mehanicheskogo povedeniya krohotnyh sostavnyh chastej mira
atomov voznikaet glubokoe protivorechie. Razmyshleniya nad etim protivorechiem
priveli izvestnogo datskogo fizika Nil'sa Bora k zaklyucheniyu, chto
klassicheskaya mehanika, na protyazhenii stoletij pretendovavshaya na osoboe
nezyblemoe polozhenie v sisteme estestvennyh nauk, dolzhna otnyne
rassmatrivat'sya kak ogranichennaya teoriya, primenimaya k makroskopicheskomu miru
povsednevnogo opyta, no utrachivayushchaya silu pri popytke primenit' ee k gorazdo
bolee tonkim tipam dvizheniya proishodyashchego vnutri razlichnyh atomov. V
kachestve probnogo fundamenta novoj obobshchennoj mehaniki, primenimoj i k
dvizheniyu krohotnyh podvizhnyh chastej atomnogo mehanizma, Bor predlozhil
gipotezu o tom, chto _iz vsego beskonechnogo raznoobraziya tipov dvizheniya,
rassmatrivaemyh v klassicheskoj mehanike, v prirode realizuetsya tol'ko
neskol'ko special'no vybrannyh tipov_. |ti razreshennye tipy dvizheniya
(nazyvaemye takzhe razreshennymi traektoriyami, ili orbitami) otbirayutsya v
sootvetstvii s opredelennymi matematicheskimi usloviyami, izvestnymi pod
nazvaniem _uslovij kvantovaniya_ v teorii Bora. YA ne stanu vhodit' zdes' v
podrobnoe obsuzhdenie etih uslovij kvantovaniya, no hochu lish' upomyanut' ob
odnom obstoyatel'stve: vse eti usloviya vybrany takim obrazom, chto nalagaemye
imi ogranicheniya ne imeyut prakticheskogo znacheniya v teh sluchayah, kogda massa
dvizhushchejsya chasticy vo mnogo raz bol'she mass, s kotorymi my vstrechaemsya v
strukture atoma. Sledovatel'no, primenitel'no k makroskopicheskim telam novaya
_mikromehanika_ privodit k tem zhe rezul'tatam, chto i staraya klassicheskaya
teoriya (_princip sootvetstviya_) i tol'ko pri perehode k mikroskopicheskim
atomnym mehanizmam raznoglasiya mezhdu staroj i novoj teoriyami stanovyatsya
sushchestvennymi. Ne vdavayas' v detali, ya hochu udovletvorit' vashe lyubopytstvo i
prodemonstrirovat' stroenie atoma s tochki zreniya teorii Bora, a imenno shemu
raspolozheniya kvantovyh orbit v atome po Boru (pervyj slajd, pozhalujsta!). Vy
vidite (sm. ris. na s. 163), razumeetsya, v sil'no uvelichennom masshtabe,
sistemu krugovyh i ellipticheskih orbit. Oni predstavlyayut edinstvenno
"razreshennye" usloviyami kvantovaniya Bora tipy dvizhenij dlya elektronov,
obrazuyushchih atomnuyu atmosferu. V to vremya kak klassicheskaya mehanika razreshaet
elektronu dvigat'sya _na lyubom_ rasstoyanii ot yadra i ne nakladyvaet
ogranichenij na ekscentrisitet (t. e. na udlinenie, ili vytyanutost') orbity,
razreshennye orbity v teorii Bora obrazuyut diskretnoe mnozhestvo s vpolne
opredelennymi harakternymi razmerami. CHisla i latinskie bukvy, stoyashchie u
kazhdoj orbity, ukazyvayut nazvanie sootvetstvuyushchej orbity v obshchej
klassifikacii. Vy mozhete, naprimer, zametit', chto bol'shie chisla
sootvetstvuyut orbitam s bol'shimi diametrami.
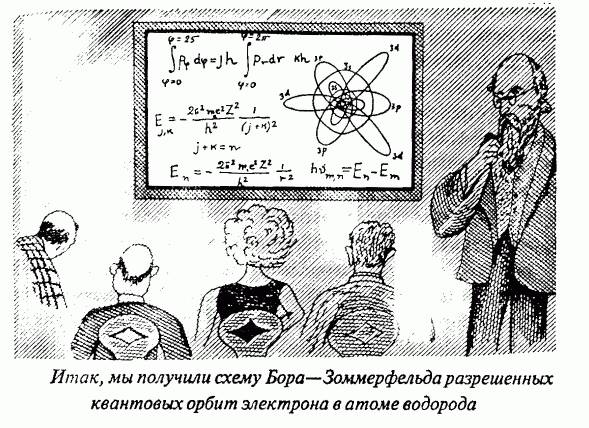 Hotya predlozhennaya Borom teoriya stroeniya atoma okazalas' neobychajno
plodotvornoj dlya ob座asneniya razlichnyh svojstv atomov i molekul, osnovnoe
ponyatie - diskretnaya kvantovaya orbita - ostavalos' ves'ma neyasnym, i chem
glubzhe fiziki pytalis' vniknut' v analiz stol' neobychnogo ogranicheniya
klassicheskoj teorii, tem bolee neyasnoj stanovilas' obshchaya kartina.
Nakonec, fiziki osoznali, v chem imenno zaklyuchaetsya slabaya storona
teorii Bora: vmesto osnovatel'noj _perestrojki_ klassicheskoj mehaniki teoriya
Bora prosto nalozhila _ogranicheniya_ na ee rezul'taty, vvedya dopolnitel'nye
usloviya, v principe chuzhdye vsej strukture klassicheskoj teorii. Pravil'noe
reshenie vsej problemy bylo polucheno lish' trinadcat' let spustya v vide tak
nazyvaemoj _volnovoj mehaniki_, izmenivshej samye osnovy klassicheskoj
mehaniki v sootvetstvii s novym kvantovym principom. Nesmotrya na to, chto na
pervyj vzglyad sistema volnovoj mehaniki mozhet pokazat'sya eshche bolee
"sumasshedshej", chem teoriya Bora, eta novaya mikromehanika predstavlyaet soboj
odnu iz naibolee posledovatel'nyh i priznannyh chastej sovremennoj
teoreticheskoj fiziki. Poskol'ku fundamental'nyj princip novoj mehaniki i, v
chastnosti, ponyatiya "neopredelennost'" i "rasplyvanie traektorij" byli
rassmotreny mnoj v odnoj iz predydushchih lekcij, ya obrashchayus' teper' k vashej
pamyati ili k vashim konspektam i hotel by vernut'sya k probleme stroeniya
atoma. Na sheme, kotoruyu vy sejchas uvidite (sleduyushchij slajd, pozhalujsta!)
(sm. ris. vnizu), izobrazheno dvizhenie atomnyh elektronov, rassmatrivaemoe s
pozicij volnovoj mehaniki, ili s tochki zreniya "rasplyvaniya orbit". Vy vidite
zdes' te zhe samye tipy dvizheniya, kotorye v ramkah klassicheskoj teorii byli
predstavleny na predydushchem slajde (edinstvennoe razlichie sostoit lish' v tom,
chto po chisto tehnicheskim prichinam kazhdyj tip dvizheniya teper' izobrazhen
otdel'no), no vmesto chetkih linij, izobrazhayushchih traektorii v teorii Bora,
teper' pered nami rasplyvchatye pyatna v polnom soglasii s fundamental'nym
_principom neopredelennosti_. Razlichnye sostoyaniya dvizheniya imeyut takie zhe
oboznacheniya, kak na predydushchem slajde, i sravnivaya oba slajda, vy zametite,
esli slegka napryazhete voobrazhenie, chto rasplyvchatye oblaka na vtorom slajde
ochen' tochno peredayut obshchie harakternye osobennosti staryh orbit Bora.
Hotya predlozhennaya Borom teoriya stroeniya atoma okazalas' neobychajno
plodotvornoj dlya ob座asneniya razlichnyh svojstv atomov i molekul, osnovnoe
ponyatie - diskretnaya kvantovaya orbita - ostavalos' ves'ma neyasnym, i chem
glubzhe fiziki pytalis' vniknut' v analiz stol' neobychnogo ogranicheniya
klassicheskoj teorii, tem bolee neyasnoj stanovilas' obshchaya kartina.
Nakonec, fiziki osoznali, v chem imenno zaklyuchaetsya slabaya storona
teorii Bora: vmesto osnovatel'noj _perestrojki_ klassicheskoj mehaniki teoriya
Bora prosto nalozhila _ogranicheniya_ na ee rezul'taty, vvedya dopolnitel'nye
usloviya, v principe chuzhdye vsej strukture klassicheskoj teorii. Pravil'noe
reshenie vsej problemy bylo polucheno lish' trinadcat' let spustya v vide tak
nazyvaemoj _volnovoj mehaniki_, izmenivshej samye osnovy klassicheskoj
mehaniki v sootvetstvii s novym kvantovym principom. Nesmotrya na to, chto na
pervyj vzglyad sistema volnovoj mehaniki mozhet pokazat'sya eshche bolee
"sumasshedshej", chem teoriya Bora, eta novaya mikromehanika predstavlyaet soboj
odnu iz naibolee posledovatel'nyh i priznannyh chastej sovremennoj
teoreticheskoj fiziki. Poskol'ku fundamental'nyj princip novoj mehaniki i, v
chastnosti, ponyatiya "neopredelennost'" i "rasplyvanie traektorij" byli
rassmotreny mnoj v odnoj iz predydushchih lekcij, ya obrashchayus' teper' k vashej
pamyati ili k vashim konspektam i hotel by vernut'sya k probleme stroeniya
atoma. Na sheme, kotoruyu vy sejchas uvidite (sleduyushchij slajd, pozhalujsta!)
(sm. ris. vnizu), izobrazheno dvizhenie atomnyh elektronov, rassmatrivaemoe s
pozicij volnovoj mehaniki, ili s tochki zreniya "rasplyvaniya orbit". Vy vidite
zdes' te zhe samye tipy dvizheniya, kotorye v ramkah klassicheskoj teorii byli
predstavleny na predydushchem slajde (edinstvennoe razlichie sostoit lish' v tom,
chto po chisto tehnicheskim prichinam kazhdyj tip dvizheniya teper' izobrazhen
otdel'no), no vmesto chetkih linij, izobrazhayushchih traektorii v teorii Bora,
teper' pered nami rasplyvchatye pyatna v polnom soglasii s fundamental'nym
_principom neopredelennosti_. Razlichnye sostoyaniya dvizheniya imeyut takie zhe
oboznacheniya, kak na predydushchem slajde, i sravnivaya oba slajda, vy zametite,
esli slegka napryazhete voobrazhenie, chto rasplyvchatye oblaka na vtorom slajde
ochen' tochno peredayut obshchie harakternye osobennosti staryh orbit Bora.
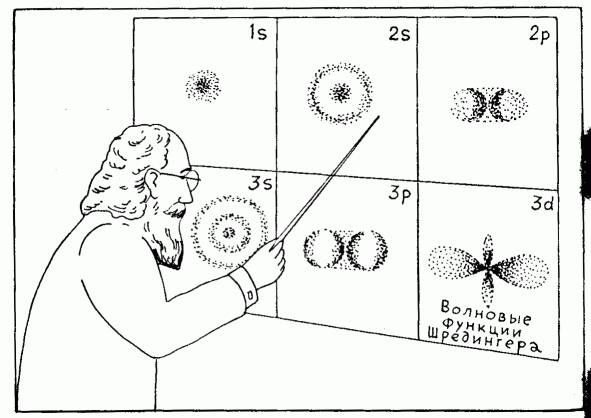 Oba slajda otchetlivo pokazyvayut, chto proishodit s dobrymi staromodnymi
traektoriyami klassicheskoj mehaniki, kogda v igru vstupaet kvant, i hotya
cheloveku neposvyashchennomu vse eto mozhet pokazat'sya fantasticheskim snom,
uchenye, rabotayushchie v mikrokosmose atomov, ne ispytyvayut osobyh trudnostej v
vospriyatii takoj kartiny.
Zavershiv na etom kratkij obzor vozmozhnyh sostoyanij dvizheniya v
elektronnoj atmosfere atoma, my obrashchaemsya teper' k vazhnoj probleme,
kasayushchejsya raspredeleniya razlichnyh atomnyh elektronov po razlichnym
dopustimym sostoyaniyam dvizheniya. Zdes' my stalkivaemsya s novym principom,
sovershenno neznakomym v makroskopicheskom mire. |tot princip vpervye byl
sformulirovan moim molodym drugom Vol'fgangom Pauli. On utverzhdaet, chto _v
soobshchestve elektronov dannogo atoma nikakie dva elektrona ne obladayut
dvizheniem odnogo i togo zhe tipa_. |to ogranichenie ne imelo by osobogo
znacheniya, esli by chislo vozmozhnyh dvizhenij bylo beskonechno veliko, kak v
klassicheskoj mehanike. No poskol'ku pravila kvantovaniya sushchestvenno
umen'shayut chislo "razreshennyh" sostoyanij dvizheniya, princip Pauli igraet ochen'
vazhnuyu rol' v atomnom mire: on obespechivaet bolee ili menee ravnomernoe
raspredelenie elektronov vokrug atomnogo yadra i meshaet elektronam
skaplivat'sya v kakom-to odnom meste.
No iz privedennoj vyshe formulirovki novogo principa ne sleduet delat'
vyvoda o tom, chto rasplyvchatye kvantovye sostoyaniya dvizheniya, izobrazhennye na
vtorom slajde, mogut byt' "zanyaty" tol'ko odnim elektronom. Dejstvitel'no,
pomimo dvizheniya po orbite kazhdyj elektron obladaet _spinom_, t.e. vrashchaetsya
vokrug sobstvennoj osi, i doktora Pauli otnyud' ne razocharuet, esli dva
elektrona okazhutsya na odnoj orbite, esli ih spiny budut napravleny v
protivopolozhnye storony. Issledovanie spina elektronov pokazyvaet, chto
skorost' vrashcheniya elektronov vokrug sobstvennoj osi vsegda odna i ta zhe i
chto napravlenie spina vsegda dolzhno byt' perpendikulyarno ploskosti orbit.
|to oznachaet, chto vozmozhny tol'ko dva razlichnyh napravleniya spina, kotorye
sootvetstvenno mozhno schitat' proishodyashchimi "po chasovoj strelke" i "protiv
chasovoj strelki".
Takim obrazom, primenitel'no k kvantovym sostoyaniyam princip Pauli mozhet
byt' sformulirovan sleduyushchim obrazom: _v kazhdom kvantovom sostoyanii dvizheniya
mogut nahodit'sya ne bolee dvuh elektronov, spiny kotoryh dolzhny byt'
napravleny v protivopolozhnye storony_. Prohodya vsyu estestvennuyu
posledovatel'nost' elementov k atomam so vse bol'shim i bol'shim chislom
elektronov, my obnaruzhim, chto razlichnye kvantovye sostoyaniya dvizheniya
postepenno zapolnyayutsya elektronami i diametr atoma monotonno vozrastaet. V
etoj svyazi nel'zya ne upomyanut' o tom, chto s tochki zreniya sily svyazi
razlichnye kvantovye sostoyaniya atomnyh elektronov mogut byt' ob容dineny v
otdel'nye gruppy (ili obolochki) s priblizitel'no ravnoj siloj svyazi. Po mere
prodvizheniya vdol' estestvennoj posledovatel'nosti elementov, my vidim, chto
odna gruppa zapolnyaetsya za drugoj i v rezul'tate posledovatel'nogo
zapolneniya elektronnyh obolochek svojstva atomov periodicheski izmenyayutsya. |to
ob座asnyaet horosho izvestnuyu periodichnost' svojstv elementov, otkrytuyu
empiricheski znamenitym russkim himikom Dmitriem Ivanovichem Mendeleevym.
Glava 12
Vnutri yadra
Sleduyushchaya lekciya, kotoruyu posetil mister Tompkins, byla posvyashchena
vnutrennemu stroeniyu yadra kak centra, vokrug kotorogo vrashchayutsya atomnye
elektrony.
- Ledi i dzhentl'meny, - nachal professor. - Vse bolee uglublyayas' v
stroenie materii, my popytaemsya teper' proniknut' nashim myslennym vzorom
vnutr' yadra, v zagadochnuyu oblast', zanimayushchuyu lish' odnu tysyachnuyu ot
milliardnoj doli obshchego ob容ma atoma. I vse zhe, nesmotrya na stol' neveroyatno
malye razmery novoj oblasti nashih isssledovanij, my obnaruzhili v nej samuyu
ozhivlennuyu deyatel'nost'. Ved' atomnoe yadro - serdce atoma, i imenno v nem,
nesmotrya na sravnitel'no malye razmery, sosredotocheno 99,97% vsej massy
atoma.
Vstupaya v oblast' atomnogo yadra posle sravnitel'no bedno naselennoj
elektronnoj atmosfery atoma, my srazu zhe budem porazheny ee neobychnoj
perenaselennost'yu. Esli elektrony atomnoj atmosfery dvizhutsya v srednem na
rasstoyaniyah, prevyshayushchih ih sobstvennyj diametr primerno v neskol'ko tysyach
raz, to chasticy, zhivushchie vnutri yadra, bukval'no tesnilis' by plechom k plechu,
bud' u nih plechi. V etom smysle kartina, kotoraya otkryvaetsya nam vnutri
yadra, ochen' napominaet kartinu obyknovennoj zhidkosti s tem lish' razlichiem,
chto vnutri yadra my vmesto molekul vstrechaem gorazdo bolee melkie i gorazdo
bolee elementarnye chasticy, izvestnye pod nazvaniem _protony_ i _nejtrony_.
Umestno zametit', chto, nesmotrya na razlichnye imena, protony i nejtrony mozhno
rassmatrivat' prosto kak dva razlichnyh zaryadovyh sostoyaniya odnoj i toj zhe
tyazheloj elementarnoj chasticy, izvestnoj pod nazvaniem nuklon. Proton
predstavlyaet soboj polozhitel'no zaryazhennyj nuklon, nejtron - elektricheski
nejtral'nyj nuklon. Ne isklyuchena vozmozhnost', chto sushchestvuyut takzhe
otricatel'no zaryazhennye nuklony, hotya ih poka nikto ne nablyudal. CHto
kasaetsya ih geometricheskih razmerov, nuklony ne slishkom otlichayutsya ot
elektronov: diametr nuklona sostavlyaet okolo 0,000 000 000 0001 sm. Odnako
nuklony gorazdo tyazhelee: na chashkah vesov proton ili nejtron mozhno
uravnovesit' 1840 elektronami. Kak ya uzhe govoril, chasticy, obrazuyushchie
atomnoe yadro, upakovany ochen' plotno i eto ob座asnyaetsya dejstviem osobyh
_yadernyh sil scepleniya_, analogichnyh silam, dejstvuyushchim mezhdu molekulami v
zhidkosti. Tak zhe kak v zhidkosti sily yadernogo scepleniya ne dayut nuklonam
polnost'yu otdelit'sya drug ot druga, no ne meshayut otnositel'nym peremeshcheniyam
nuklonov. Takim obrazom, yadernaya materiya v kakoj-to stepeni obladaet
tekuchest'yu i, ne buduchi vozmushchaema vneshnimi silami, prinimaet formu
sfericheskoj kapli, kak obychnaya kaplya zhidkosti. Na sheme, kotoruyu ya vam
sejchas pokazhu, uslovno izobrazheny razlichnye tipy atomnyh yader, obrazovannyh
iz protonov i nejtronov. Prostejshee yadro vodoroda sostoit vsego lish' iz
odnogo protona, v to vremya kak samoe slozhnoe yadro urana sostoit iz 92
protonov i 142 nejtronov. Razumeetsya, razglyadyvaya eti kartinki, ne sleduet
upuskat' iz vidu, chto pered vami lish' ves'ma uslovnye izobrazheniya real'nyh
yader, poskol'ku v silu fundamental'nogo principa neopredelennosti kvantovoj
teorii polozhenie kazhdogo nuklona v dejstvitel'nosti "razmazano" po vsemu
ob容mu yadra.
Kak ya uzhe upominal, chasticy, obrazuyushchie atomnoe yadro, uderzhivayutsya
vmeste moshchnymi silami scepleniya, no pomimo etih sil prityazheniya sushchestvuyut
takzhe sily drugogo roda, dejstvuyushchie v protivopolozhnom napravlenii.
Dejstvitel'no, protony, na dolyu kotoryh prihoditsya primerno polovina
nuklonnogo naseleniya, nesut polozhitel'nyj zaryad. Sledovatel'no, mezhdu nimi
dejstvuyut sily ottalkivaniya - tak nazyvaemye kulonovskie sily. Dlya legkih
yader, elektricheskij zaryad kotoryh sravnitel'no mal, eto kulonovskoe
ottalkivanie ne imeet osobogo znacheniya, no v bolee tyazhelyh yadrah s b_o_l'shim
elektricheskim zaryadom kulonovskie sily nachinayut sostavlyat' ser'eznuyu
konkurenciyu silam yadernogo scepleniya. Kak tol'ko eto proizojdet, yadro
utrachivaet stabil'nost' i mozhet ispustit' kakie-nibud' iz sostavlyayushchih ego
chastic. Imenno tak vedut sebya nekotorye elementy, raspolozhennye v samom
konce Periodicheskoj sistemy i izvestnye pod nazvaniem _radioaktivnye
elementy_.
Oba slajda otchetlivo pokazyvayut, chto proishodit s dobrymi staromodnymi
traektoriyami klassicheskoj mehaniki, kogda v igru vstupaet kvant, i hotya
cheloveku neposvyashchennomu vse eto mozhet pokazat'sya fantasticheskim snom,
uchenye, rabotayushchie v mikrokosmose atomov, ne ispytyvayut osobyh trudnostej v
vospriyatii takoj kartiny.
Zavershiv na etom kratkij obzor vozmozhnyh sostoyanij dvizheniya v
elektronnoj atmosfere atoma, my obrashchaemsya teper' k vazhnoj probleme,
kasayushchejsya raspredeleniya razlichnyh atomnyh elektronov po razlichnym
dopustimym sostoyaniyam dvizheniya. Zdes' my stalkivaemsya s novym principom,
sovershenno neznakomym v makroskopicheskom mire. |tot princip vpervye byl
sformulirovan moim molodym drugom Vol'fgangom Pauli. On utverzhdaet, chto _v
soobshchestve elektronov dannogo atoma nikakie dva elektrona ne obladayut
dvizheniem odnogo i togo zhe tipa_. |to ogranichenie ne imelo by osobogo
znacheniya, esli by chislo vozmozhnyh dvizhenij bylo beskonechno veliko, kak v
klassicheskoj mehanike. No poskol'ku pravila kvantovaniya sushchestvenno
umen'shayut chislo "razreshennyh" sostoyanij dvizheniya, princip Pauli igraet ochen'
vazhnuyu rol' v atomnom mire: on obespechivaet bolee ili menee ravnomernoe
raspredelenie elektronov vokrug atomnogo yadra i meshaet elektronam
skaplivat'sya v kakom-to odnom meste.
No iz privedennoj vyshe formulirovki novogo principa ne sleduet delat'
vyvoda o tom, chto rasplyvchatye kvantovye sostoyaniya dvizheniya, izobrazhennye na
vtorom slajde, mogut byt' "zanyaty" tol'ko odnim elektronom. Dejstvitel'no,
pomimo dvizheniya po orbite kazhdyj elektron obladaet _spinom_, t.e. vrashchaetsya
vokrug sobstvennoj osi, i doktora Pauli otnyud' ne razocharuet, esli dva
elektrona okazhutsya na odnoj orbite, esli ih spiny budut napravleny v
protivopolozhnye storony. Issledovanie spina elektronov pokazyvaet, chto
skorost' vrashcheniya elektronov vokrug sobstvennoj osi vsegda odna i ta zhe i
chto napravlenie spina vsegda dolzhno byt' perpendikulyarno ploskosti orbit.
|to oznachaet, chto vozmozhny tol'ko dva razlichnyh napravleniya spina, kotorye
sootvetstvenno mozhno schitat' proishodyashchimi "po chasovoj strelke" i "protiv
chasovoj strelki".
Takim obrazom, primenitel'no k kvantovym sostoyaniyam princip Pauli mozhet
byt' sformulirovan sleduyushchim obrazom: _v kazhdom kvantovom sostoyanii dvizheniya
mogut nahodit'sya ne bolee dvuh elektronov, spiny kotoryh dolzhny byt'
napravleny v protivopolozhnye storony_. Prohodya vsyu estestvennuyu
posledovatel'nost' elementov k atomam so vse bol'shim i bol'shim chislom
elektronov, my obnaruzhim, chto razlichnye kvantovye sostoyaniya dvizheniya
postepenno zapolnyayutsya elektronami i diametr atoma monotonno vozrastaet. V
etoj svyazi nel'zya ne upomyanut' o tom, chto s tochki zreniya sily svyazi
razlichnye kvantovye sostoyaniya atomnyh elektronov mogut byt' ob容dineny v
otdel'nye gruppy (ili obolochki) s priblizitel'no ravnoj siloj svyazi. Po mere
prodvizheniya vdol' estestvennoj posledovatel'nosti elementov, my vidim, chto
odna gruppa zapolnyaetsya za drugoj i v rezul'tate posledovatel'nogo
zapolneniya elektronnyh obolochek svojstva atomov periodicheski izmenyayutsya. |to
ob座asnyaet horosho izvestnuyu periodichnost' svojstv elementov, otkrytuyu
empiricheski znamenitym russkim himikom Dmitriem Ivanovichem Mendeleevym.
Glava 12
Vnutri yadra
Sleduyushchaya lekciya, kotoruyu posetil mister Tompkins, byla posvyashchena
vnutrennemu stroeniyu yadra kak centra, vokrug kotorogo vrashchayutsya atomnye
elektrony.
- Ledi i dzhentl'meny, - nachal professor. - Vse bolee uglublyayas' v
stroenie materii, my popytaemsya teper' proniknut' nashim myslennym vzorom
vnutr' yadra, v zagadochnuyu oblast', zanimayushchuyu lish' odnu tysyachnuyu ot
milliardnoj doli obshchego ob容ma atoma. I vse zhe, nesmotrya na stol' neveroyatno
malye razmery novoj oblasti nashih isssledovanij, my obnaruzhili v nej samuyu
ozhivlennuyu deyatel'nost'. Ved' atomnoe yadro - serdce atoma, i imenno v nem,
nesmotrya na sravnitel'no malye razmery, sosredotocheno 99,97% vsej massy
atoma.
Vstupaya v oblast' atomnogo yadra posle sravnitel'no bedno naselennoj
elektronnoj atmosfery atoma, my srazu zhe budem porazheny ee neobychnoj
perenaselennost'yu. Esli elektrony atomnoj atmosfery dvizhutsya v srednem na
rasstoyaniyah, prevyshayushchih ih sobstvennyj diametr primerno v neskol'ko tysyach
raz, to chasticy, zhivushchie vnutri yadra, bukval'no tesnilis' by plechom k plechu,
bud' u nih plechi. V etom smysle kartina, kotoraya otkryvaetsya nam vnutri
yadra, ochen' napominaet kartinu obyknovennoj zhidkosti s tem lish' razlichiem,
chto vnutri yadra my vmesto molekul vstrechaem gorazdo bolee melkie i gorazdo
bolee elementarnye chasticy, izvestnye pod nazvaniem _protony_ i _nejtrony_.
Umestno zametit', chto, nesmotrya na razlichnye imena, protony i nejtrony mozhno
rassmatrivat' prosto kak dva razlichnyh zaryadovyh sostoyaniya odnoj i toj zhe
tyazheloj elementarnoj chasticy, izvestnoj pod nazvaniem nuklon. Proton
predstavlyaet soboj polozhitel'no zaryazhennyj nuklon, nejtron - elektricheski
nejtral'nyj nuklon. Ne isklyuchena vozmozhnost', chto sushchestvuyut takzhe
otricatel'no zaryazhennye nuklony, hotya ih poka nikto ne nablyudal. CHto
kasaetsya ih geometricheskih razmerov, nuklony ne slishkom otlichayutsya ot
elektronov: diametr nuklona sostavlyaet okolo 0,000 000 000 0001 sm. Odnako
nuklony gorazdo tyazhelee: na chashkah vesov proton ili nejtron mozhno
uravnovesit' 1840 elektronami. Kak ya uzhe govoril, chasticy, obrazuyushchie
atomnoe yadro, upakovany ochen' plotno i eto ob座asnyaetsya dejstviem osobyh
_yadernyh sil scepleniya_, analogichnyh silam, dejstvuyushchim mezhdu molekulami v
zhidkosti. Tak zhe kak v zhidkosti sily yadernogo scepleniya ne dayut nuklonam
polnost'yu otdelit'sya drug ot druga, no ne meshayut otnositel'nym peremeshcheniyam
nuklonov. Takim obrazom, yadernaya materiya v kakoj-to stepeni obladaet
tekuchest'yu i, ne buduchi vozmushchaema vneshnimi silami, prinimaet formu
sfericheskoj kapli, kak obychnaya kaplya zhidkosti. Na sheme, kotoruyu ya vam
sejchas pokazhu, uslovno izobrazheny razlichnye tipy atomnyh yader, obrazovannyh
iz protonov i nejtronov. Prostejshee yadro vodoroda sostoit vsego lish' iz
odnogo protona, v to vremya kak samoe slozhnoe yadro urana sostoit iz 92
protonov i 142 nejtronov. Razumeetsya, razglyadyvaya eti kartinki, ne sleduet
upuskat' iz vidu, chto pered vami lish' ves'ma uslovnye izobrazheniya real'nyh
yader, poskol'ku v silu fundamental'nogo principa neopredelennosti kvantovoj
teorii polozhenie kazhdogo nuklona v dejstvitel'nosti "razmazano" po vsemu
ob容mu yadra.
Kak ya uzhe upominal, chasticy, obrazuyushchie atomnoe yadro, uderzhivayutsya
vmeste moshchnymi silami scepleniya, no pomimo etih sil prityazheniya sushchestvuyut
takzhe sily drugogo roda, dejstvuyushchie v protivopolozhnom napravlenii.
Dejstvitel'no, protony, na dolyu kotoryh prihoditsya primerno polovina
nuklonnogo naseleniya, nesut polozhitel'nyj zaryad. Sledovatel'no, mezhdu nimi
dejstvuyut sily ottalkivaniya - tak nazyvaemye kulonovskie sily. Dlya legkih
yader, elektricheskij zaryad kotoryh sravnitel'no mal, eto kulonovskoe
ottalkivanie ne imeet osobogo znacheniya, no v bolee tyazhelyh yadrah s b_o_l'shim
elektricheskim zaryadom kulonovskie sily nachinayut sostavlyat' ser'eznuyu
konkurenciyu silam yadernogo scepleniya. Kak tol'ko eto proizojdet, yadro
utrachivaet stabil'nost' i mozhet ispustit' kakie-nibud' iz sostavlyayushchih ego
chastic. Imenno tak vedut sebya nekotorye elementy, raspolozhennye v samom
konce Periodicheskoj sistemy i izvestnye pod nazvaniem _radioaktivnye
elementy_.
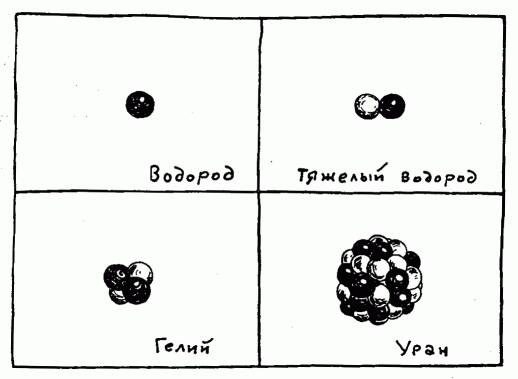 Iz privedennyh vyshe obshchih soobrazhenij vy mozhete zaklyuchit', chto takie
tyazhelye nestabil'nye yadra dolzhny ispuskat' protony, tak kak nejtrony ne
nesut nikakogo elektricheskogo zaryada, i poetomu na nih ne dejstvuyut sily
kulonovskogo ottalkivaniya. Odnako, kak pokazyvayut eksperimenty, nekotorye
radioaktivnye yadra ispuskayut tak nazyvaemye _al'fa-chasticy_ (yadra geliya), t.
e. slozhnye obrazovaniya, kazhdoe iz kotoryh sostoit iz dvuh protonov i dvuh
nejtronov. Ob座asnyaetsya eto osoboj gruppirovkoj chastic, obrazuyushchih atomnoe
yadro. Delo v tom, chto kombinaciya dvuh protonov i dvuh nejtronov, obrazuyushchaya
al'fu-chasticu, otlichaetsya povyshennoj stabil'nost'yu, i poetomu legche otorvat'
takuyu gruppu celikom, chem razdelit' ee na otdel'nye protony i nejtrony.
Kak vy, veroyatno, znaete, yavlenie radioaktivnogo raspada bylo vpervye
otkryto francuzskim fizikom Anri Bekkerelem, a znamenityj britanskij fizik
lord Rezerford, ch'e imya ya uzhe upominal v drugoj svyazi, kotoromu nauka stol'
mnogim obyazana za ego vazhnye otkrytiya v fizike atomnogo yadra, predlozhil
ob座asnenie radioaktivnogo raspada kak spontannogo, t. e. samoproizvol'nogo,
raspada atomnogo yadra na chasti.
Odna iz naibolee zamechatel'nyh osobennostej al'fa-raspada sostoit v
inogda neobychajno dolgih periodah vremeni, neobhodimyh al'fa-chasticam, chtoby
"vybrat'sya" iz atomnogo yadra na svobodu. Dlya _urana_ i _toriya_ etot period
sostavlyaet, po ocenkam, milliardy let, dlya radiya - okolo shestnadcati
stoletij, i hotya sushchestvuyut elementy, dlya kotoryh al'fa-raspad proishodit v
doli sekundy, prodolzhitel'nost' ih zhizni mozhno takzhe schitat' ochen' dolgoj po
sravneniyu s bystrotoj ih vnutriyadernogo dvizheniya.
CHto zhe zastavlyaet al'fa-chasticu ostavat'sya vnutri yadra na protyazhenii
inogda mnogih milliardov let? I esli al'fa-chastica tak dolgo nahoditsya
vnutri yadra, to chto zastavlyaet ee vse zhe pokinut' ego?
Dlya otveta na eti voprosy nam neobhodimo predvaritel'no uznat' nemnogo
bol'she o sravnitel'noj intensivnosti sil vnutriyadernogo scepleniya i
elektrostaticheskih sil ottalkivaniya, dejstvuyushchih na chasticu, kotoraya
pokidaet atomnoe yadro. Tshchatel'noe eksperimental'noe izuchenie etih sil bylo
provedeno Rezerfordom, kotoryj vospol'zovalsya metodom tak nazyvaemoj
_atomnoj bombardirovki_. V svoih znamenityh eksperimentah, vypolnennyh v
Kavendishskoj laboratorii, Rezerford napravlyal puchok bystro dvizhushchihsya
al'fa-chastic, ispuskaemyh kakim-nibud' radioaktivnym veshchestvom, na mishen' i
nablyudal otkloneniya (rasseyanie) etih atomnyh snaryadov pri stolknovenii ih s
yadrami bombardiruemogo veshchestva. |ksperimenty Rezerforda ubeditel'no
pokazali, chto na bol'shih rasstoyaniyah ot atomnogo yadra al'fa-chasticy
ispytyvali sil'noe ottalkivanie elektricheskimi silami zaryada yadra, no
ottalkivanie smenyalos' sil'nym prityazheniem v teh sluchayah, kogda
al'fa-chasticy proletali vplotnuyu ot vneshnih granic yadernoj oblasti. Vy
mozhete skazat', chto atomnoe yadro v kakoj-to mere analogichno kreposti,
okruzhennoj so vseh storon vysokimi krutymi stenami, ne pozvolyayushchimi chasticam
ni popast' vnutr', ni bezhat' naruzhu. No samyj porazitel'nyj rezul'tat
eksperimentov Rezerforda sostoyal v ustanovlenii sleduyushchego fakta:
_al'fa-chasticy, vyletayushchie iz yadra pri radioaktivnom raspade ili pronikayushchie
vnutr' yadra pri bombardirovke izvne, obladayut men'shej energiej, chem
trebovalos' by dlya preodoleniya vysoty sten kreposti, ili potencial'nogo
bar'era_, kak my obychno govorim. |to otkrytie Rezerforda polnost'yu
protivorechilo vsem fundamental'nym predstavleniyam klassicheskoj mehaniki. V
samom dele, kak mozhno ozhidat', chto myach perekatitsya cherez vershinu holma, esli
vy brosili ego s energiej, nedostatochnoj dlya pod容ma na vershinu holma?
Klassicheskaya fizika mogla lish' shiroko raskryt' glaza ot udivleniya i
vyskazat' predpolozhenie o tom, chto v eksperimenty Rezerforda gde-to vkralas'
kakaya-to oshibka.
No v dejstvitel'nosti nikakoj oshibki ne bylo, i esli kto-nibud' i
oshibalsya, to ne lord Rezerford, a... klassicheskaya mehanika! Situaciyu
proyasnili odnovremenno moj dobryj drug doktor Gamov i doktora Ronal'd Gernej
i |. U. London. Oni obratili vnimanie na to, chto nikakih trudnostej ne
voznikaet, esli podojti k probleme s tochki zreniya sovremennoj kvantovoj
teorii. Dejstvitel'no, kak my znaem, sovremennaya kvantovaya fizika otvergaet
chetko opredelennye traektorii-linii klassicheskoj teorii i zamenyaet ih
rasplyvchatymi prizrachnymi sledami. Podobno tomu, kak dobroe staromodnoe
prividenie moglo bez truda prohodit' skvoz' tolstye kamennye steny
starinnogo zamka, tak prizrachnye traektorii mogut pronikat' skvoz'
potencial'nye bar'ery, kotorye s klassicheskoj tochki zreniya kazalis'
sovershenno nepronicaemymi.
Ne dumajte, pozhalujsta, budto ya shuchu: pronicaemost' potencial'nyh
bar'erov dlya chastic s nedostatochnoj energiej yavlyaetsya pryamym matematicheskim
sledstviem iz fundamental'nyh uravnenij novoj kvantovoj mehaniki i sluzhit
ves'ma ubeditel'noj illyustraciej odnogo iz naibolee sushchestvennyh razlichij
mezhdu starymi i novymi predstavleniyami o dvizhenii. No hotya novaya mehanika
dopuskaet stol' neobychnye effekty, ona delaet eto tol'ko pri ves'ma sil'nyh
ogranicheniyah: v bol'shinstve sluchaev veroyatnost' peresecheniya bar'era
chrezvychajno mala, i popavshej v temnicu yadra chastice pridetsya neveroyatno
bol'shoe chislo raz brosat'sya na steny, prezhde chem ee popytki vybrat'sya na
svobodu uvenchayutsya uspehom. Kvantovaya teoriya daet nam tochnye pravila dlya
vychisleniya veroyatnosti takogo pobega. Bylo pokazano, chto nablyudaemye periody
al'fa-raspada nahodyatsya v polnom sootvetstvii s predskazaniyami teorii. V
sluchae al'fa-chastic, bombardiruyushchih atomnoe yadro izvne, rezul'taty
kvantovo-mehanicheskih raschetov nahodyatsya v velikolepnom sootvetstvii s
eksperimentom.
Prezhde chem ya prodolzhu svoyu lekciyu, mne hotelos' by pokazat' vam
nekotorye fotografii processov raspada razlichnyh yader, bombardiruemyh
atomnymi snaryadami vysokoj energii (pervyj slajd, pozhalujsta!).
Na etom slajde (sm. ris. na s. 174) vy vidite dva razlichnyh raspada,
sfotografirovannyh v puzyr'kovoj kamere, o kotoroj ya govoril v svoej
predydushchej lekcii. Na snimke (A) vy vidite stolknovenie yadra azota s bystroj
al'fa-chasticej. |to pervyj iz kogda-libo sdelannyh snimkov iskusstvennoj
transmutacii (prevrashcheniya) elementov. |tim snimkom my obyazany ucheniku lorda
Rezerforda Patriku Blekketu. Otchetlivo vidno bol'shoe chislo trekov
al'fa-chastic, ispuskaemyh moshchnym istochnikom al'fa-chastic. Bol'shinstvo
al'fa-chastic proletayut vse pole zreniya, ne preterpevaya ni odnogo ser'eznogo
stolknoveniya. Trek al'fa-chastic ostanavlivaetsya vot zdes', i vy vidite, kak
iz tochki stolknoveniya vyhodyat dva drugih treka. Dlinnyj tonkij trek
prinadlezhit protonu, vybitomu iz yadra azota, v to vremya kak korotkij tolstyj
trek sootvetstvuet otdache samogo yadra. No eto bolee uzhe ne yadro azota,
poskol'ku, poteryav proton i poglotiv naletevshuyu al'fa-chasticu, yadro azota
prevratilos' v yadro kisloroda. Takim obrazom, my stanovimsya svidetelyami
alhimicheskogo prevrashcheniya azota v kislorod s vodorodom v kachestve pobochnogo
produkta.
Na snimkah (B), (V) vy vidite raspad yadra pri stolknovenii s
iskusstvenno uskorennym protonom. Puchok bystryh protonov sozdaetsya
special'noj mashinoj, rabotayushchej pod vysokim napryazheniem i izvestnoj publike
pod nazvaniem "atomnaya drobilka", i postupaet v kameru cherez dlinnuyu trubku,
konec kotoroj viden na snimkah. Mishen', v dannom sluchae tonkij sloj bora,
pomeshchaetsya u otkrytogo konca trubki s takim raschetom, chtoby oskolki yadra,
voznikshie pri stolknovenii, dolzhny byli proletat' skvoz' vozduh v kamere,
obrazuya tumannye treki. Kak vy vidite na snimke (V), yadro bora pri
stolknovenii s protonom, raspadaetsya na tri chasti, i, s uchetom sohraneniya
elektricheskogo zaryada, my prihodim k zaklyucheniyu, chto kazhdyj iz oskolkov
deleniya predstavlyaet soboj al'fa-chasticu, t. e. yadro geliya. |ti dva yadernyh
prevrashcheniya predstavlyayut ves'ma tipichnye primery neskol'kih soten drugih
yadernyh prevrashchenij, issledovannyh sovremennoj eksperimental'noj fizikoj. Vo
vseh prevrashcheniyah takogo roda, izvestnyh pod nazvaniem _yadernye reakcii
zameshcheniya_, naletayushchaya chastica (proton, nejtron ili al'fa-chastica) pronikaet
v yadro, vybivaet kakuyu-to druguyu chasticu i ostaetsya na ee meste. Sushchestvuet
zameshchenie protona al'fa-chasticej, al'fa-chasticy protonom, protona nejtronom
i t.d. Vo vseh takih prevrashcheniyah novyj element, obrazovavshijsya v rezul'tate
reakcii, yavlyaetsya blizkim sosedom bombardiruemogo elementa v Periodicheskoj
sisteme.
No lish' sravnitel'no nedavno, pered vtoroj mirovoj vojnoj, dva nemeckih
himika O. Gan i F. SHtrassman otkryli sovershenno novyj tip yadernogo
prevrashcheniya, v kotorom _tyazheloe yadro raspadaetsya na dve ravnye poloviny s
vysvobozhdeniem ogromnogo kolichestva energii_. Na sleduyushchem slajde (sleduyushchij
slajd, pozhalujsta!) vy vidite (sm. s. 175) na snimke (B) dva oskolka yadra
urana, razletayushchihsya v raznye storony ot tonkoj uranovoj provolochki. |to
yavlenie, poluchivshee nazvanie _rasshcheplenie yadra_, vpervye nablyudalos' pri
bombardirovke urana puchkom nejtronov, no vskore fiziki obnaruzhili, chto i
drugie elementy, raspolozhennye v konce Periodicheskoj sistemy, obladayut
analogichnymi svojstvami. |ti tyazhelye yadra uzhe nahodyatsya u poroga svoej
stabil'nosti i malejshee vozmushchenie, vyzyvaemoe stolknoveniem s nejtronom,
dostatochno, chtoby oni raspalis' na dva oskolka, kak raspadaetsya na chasti
chrezmerno krupnaya kaplya rtuti. Nestabil'nost' tyazhelyh yader prolivaet svet na
vopros o tom, pochemu v prirode sushchestvuet tol'ko 92 elementa. Lyuboe yadro
tyazhelee urana ne mozhet sushchestvovat' skol'ko-nibud' prodolzhitel'noe vremya i
nemedlenno raspadaetsya na bolee melkie oskolki. YAvlenie rasshchepleniya yadra
predstavlyaet nemalyj interes i s prakticheskoj tochki zreniya, tak kak
otkryvaet opredelennye vozmozhnosti dlya ispol'zovaniya yadernoj energii. Delo v
tom, chto pri raspade yadra na dve polovinki iz yadra vyletaet neskol'ko
nejtronov, kotorye mogut vyzvat' rasshcheplenie sosednih yader. Dal'nejshee
rasprostranenie takogo processa mozhet privesti k vzryvnoj reakcii, pri
kotoroj vsya energiya, zapasennaya v yadrah, vysvobozhdaetsya za maluyu dolyu
sekundy. Esli vspomnit', chto yadernaya energiya, hranyashchayasya v odnom funte
urana, ekvivalentna energeticheskomu soderzhaniyu desyati tonn uglya, to stanet
yasno, chto vozmozhnost' vysvobozhdeniya yadernoj energii mogla by vyzvat'
glubokie peremeny v nashej ekonomike.
Iz privedennyh vyshe obshchih soobrazhenij vy mozhete zaklyuchit', chto takie
tyazhelye nestabil'nye yadra dolzhny ispuskat' protony, tak kak nejtrony ne
nesut nikakogo elektricheskogo zaryada, i poetomu na nih ne dejstvuyut sily
kulonovskogo ottalkivaniya. Odnako, kak pokazyvayut eksperimenty, nekotorye
radioaktivnye yadra ispuskayut tak nazyvaemye _al'fa-chasticy_ (yadra geliya), t.
e. slozhnye obrazovaniya, kazhdoe iz kotoryh sostoit iz dvuh protonov i dvuh
nejtronov. Ob座asnyaetsya eto osoboj gruppirovkoj chastic, obrazuyushchih atomnoe
yadro. Delo v tom, chto kombinaciya dvuh protonov i dvuh nejtronov, obrazuyushchaya
al'fu-chasticu, otlichaetsya povyshennoj stabil'nost'yu, i poetomu legche otorvat'
takuyu gruppu celikom, chem razdelit' ee na otdel'nye protony i nejtrony.
Kak vy, veroyatno, znaete, yavlenie radioaktivnogo raspada bylo vpervye
otkryto francuzskim fizikom Anri Bekkerelem, a znamenityj britanskij fizik
lord Rezerford, ch'e imya ya uzhe upominal v drugoj svyazi, kotoromu nauka stol'
mnogim obyazana za ego vazhnye otkrytiya v fizike atomnogo yadra, predlozhil
ob座asnenie radioaktivnogo raspada kak spontannogo, t. e. samoproizvol'nogo,
raspada atomnogo yadra na chasti.
Odna iz naibolee zamechatel'nyh osobennostej al'fa-raspada sostoit v
inogda neobychajno dolgih periodah vremeni, neobhodimyh al'fa-chasticam, chtoby
"vybrat'sya" iz atomnogo yadra na svobodu. Dlya _urana_ i _toriya_ etot period
sostavlyaet, po ocenkam, milliardy let, dlya radiya - okolo shestnadcati
stoletij, i hotya sushchestvuyut elementy, dlya kotoryh al'fa-raspad proishodit v
doli sekundy, prodolzhitel'nost' ih zhizni mozhno takzhe schitat' ochen' dolgoj po
sravneniyu s bystrotoj ih vnutriyadernogo dvizheniya.
CHto zhe zastavlyaet al'fa-chasticu ostavat'sya vnutri yadra na protyazhenii
inogda mnogih milliardov let? I esli al'fa-chastica tak dolgo nahoditsya
vnutri yadra, to chto zastavlyaet ee vse zhe pokinut' ego?
Dlya otveta na eti voprosy nam neobhodimo predvaritel'no uznat' nemnogo
bol'she o sravnitel'noj intensivnosti sil vnutriyadernogo scepleniya i
elektrostaticheskih sil ottalkivaniya, dejstvuyushchih na chasticu, kotoraya
pokidaet atomnoe yadro. Tshchatel'noe eksperimental'noe izuchenie etih sil bylo
provedeno Rezerfordom, kotoryj vospol'zovalsya metodom tak nazyvaemoj
_atomnoj bombardirovki_. V svoih znamenityh eksperimentah, vypolnennyh v
Kavendishskoj laboratorii, Rezerford napravlyal puchok bystro dvizhushchihsya
al'fa-chastic, ispuskaemyh kakim-nibud' radioaktivnym veshchestvom, na mishen' i
nablyudal otkloneniya (rasseyanie) etih atomnyh snaryadov pri stolknovenii ih s
yadrami bombardiruemogo veshchestva. |ksperimenty Rezerforda ubeditel'no
pokazali, chto na bol'shih rasstoyaniyah ot atomnogo yadra al'fa-chasticy
ispytyvali sil'noe ottalkivanie elektricheskimi silami zaryada yadra, no
ottalkivanie smenyalos' sil'nym prityazheniem v teh sluchayah, kogda
al'fa-chasticy proletali vplotnuyu ot vneshnih granic yadernoj oblasti. Vy
mozhete skazat', chto atomnoe yadro v kakoj-to mere analogichno kreposti,
okruzhennoj so vseh storon vysokimi krutymi stenami, ne pozvolyayushchimi chasticam
ni popast' vnutr', ni bezhat' naruzhu. No samyj porazitel'nyj rezul'tat
eksperimentov Rezerforda sostoyal v ustanovlenii sleduyushchego fakta:
_al'fa-chasticy, vyletayushchie iz yadra pri radioaktivnom raspade ili pronikayushchie
vnutr' yadra pri bombardirovke izvne, obladayut men'shej energiej, chem
trebovalos' by dlya preodoleniya vysoty sten kreposti, ili potencial'nogo
bar'era_, kak my obychno govorim. |to otkrytie Rezerforda polnost'yu
protivorechilo vsem fundamental'nym predstavleniyam klassicheskoj mehaniki. V
samom dele, kak mozhno ozhidat', chto myach perekatitsya cherez vershinu holma, esli
vy brosili ego s energiej, nedostatochnoj dlya pod容ma na vershinu holma?
Klassicheskaya fizika mogla lish' shiroko raskryt' glaza ot udivleniya i
vyskazat' predpolozhenie o tom, chto v eksperimenty Rezerforda gde-to vkralas'
kakaya-to oshibka.
No v dejstvitel'nosti nikakoj oshibki ne bylo, i esli kto-nibud' i
oshibalsya, to ne lord Rezerford, a... klassicheskaya mehanika! Situaciyu
proyasnili odnovremenno moj dobryj drug doktor Gamov i doktora Ronal'd Gernej
i |. U. London. Oni obratili vnimanie na to, chto nikakih trudnostej ne
voznikaet, esli podojti k probleme s tochki zreniya sovremennoj kvantovoj
teorii. Dejstvitel'no, kak my znaem, sovremennaya kvantovaya fizika otvergaet
chetko opredelennye traektorii-linii klassicheskoj teorii i zamenyaet ih
rasplyvchatymi prizrachnymi sledami. Podobno tomu, kak dobroe staromodnoe
prividenie moglo bez truda prohodit' skvoz' tolstye kamennye steny
starinnogo zamka, tak prizrachnye traektorii mogut pronikat' skvoz'
potencial'nye bar'ery, kotorye s klassicheskoj tochki zreniya kazalis'
sovershenno nepronicaemymi.
Ne dumajte, pozhalujsta, budto ya shuchu: pronicaemost' potencial'nyh
bar'erov dlya chastic s nedostatochnoj energiej yavlyaetsya pryamym matematicheskim
sledstviem iz fundamental'nyh uravnenij novoj kvantovoj mehaniki i sluzhit
ves'ma ubeditel'noj illyustraciej odnogo iz naibolee sushchestvennyh razlichij
mezhdu starymi i novymi predstavleniyami o dvizhenii. No hotya novaya mehanika
dopuskaet stol' neobychnye effekty, ona delaet eto tol'ko pri ves'ma sil'nyh
ogranicheniyah: v bol'shinstve sluchaev veroyatnost' peresecheniya bar'era
chrezvychajno mala, i popavshej v temnicu yadra chastice pridetsya neveroyatno
bol'shoe chislo raz brosat'sya na steny, prezhde chem ee popytki vybrat'sya na
svobodu uvenchayutsya uspehom. Kvantovaya teoriya daet nam tochnye pravila dlya
vychisleniya veroyatnosti takogo pobega. Bylo pokazano, chto nablyudaemye periody
al'fa-raspada nahodyatsya v polnom sootvetstvii s predskazaniyami teorii. V
sluchae al'fa-chastic, bombardiruyushchih atomnoe yadro izvne, rezul'taty
kvantovo-mehanicheskih raschetov nahodyatsya v velikolepnom sootvetstvii s
eksperimentom.
Prezhde chem ya prodolzhu svoyu lekciyu, mne hotelos' by pokazat' vam
nekotorye fotografii processov raspada razlichnyh yader, bombardiruemyh
atomnymi snaryadami vysokoj energii (pervyj slajd, pozhalujsta!).
Na etom slajde (sm. ris. na s. 174) vy vidite dva razlichnyh raspada,
sfotografirovannyh v puzyr'kovoj kamere, o kotoroj ya govoril v svoej
predydushchej lekcii. Na snimke (A) vy vidite stolknovenie yadra azota s bystroj
al'fa-chasticej. |to pervyj iz kogda-libo sdelannyh snimkov iskusstvennoj
transmutacii (prevrashcheniya) elementov. |tim snimkom my obyazany ucheniku lorda
Rezerforda Patriku Blekketu. Otchetlivo vidno bol'shoe chislo trekov
al'fa-chastic, ispuskaemyh moshchnym istochnikom al'fa-chastic. Bol'shinstvo
al'fa-chastic proletayut vse pole zreniya, ne preterpevaya ni odnogo ser'eznogo
stolknoveniya. Trek al'fa-chastic ostanavlivaetsya vot zdes', i vy vidite, kak
iz tochki stolknoveniya vyhodyat dva drugih treka. Dlinnyj tonkij trek
prinadlezhit protonu, vybitomu iz yadra azota, v to vremya kak korotkij tolstyj
trek sootvetstvuet otdache samogo yadra. No eto bolee uzhe ne yadro azota,
poskol'ku, poteryav proton i poglotiv naletevshuyu al'fa-chasticu, yadro azota
prevratilos' v yadro kisloroda. Takim obrazom, my stanovimsya svidetelyami
alhimicheskogo prevrashcheniya azota v kislorod s vodorodom v kachestve pobochnogo
produkta.
Na snimkah (B), (V) vy vidite raspad yadra pri stolknovenii s
iskusstvenno uskorennym protonom. Puchok bystryh protonov sozdaetsya
special'noj mashinoj, rabotayushchej pod vysokim napryazheniem i izvestnoj publike
pod nazvaniem "atomnaya drobilka", i postupaet v kameru cherez dlinnuyu trubku,
konec kotoroj viden na snimkah. Mishen', v dannom sluchae tonkij sloj bora,
pomeshchaetsya u otkrytogo konca trubki s takim raschetom, chtoby oskolki yadra,
voznikshie pri stolknovenii, dolzhny byli proletat' skvoz' vozduh v kamere,
obrazuya tumannye treki. Kak vy vidite na snimke (V), yadro bora pri
stolknovenii s protonom, raspadaetsya na tri chasti, i, s uchetom sohraneniya
elektricheskogo zaryada, my prihodim k zaklyucheniyu, chto kazhdyj iz oskolkov
deleniya predstavlyaet soboj al'fa-chasticu, t. e. yadro geliya. |ti dva yadernyh
prevrashcheniya predstavlyayut ves'ma tipichnye primery neskol'kih soten drugih
yadernyh prevrashchenij, issledovannyh sovremennoj eksperimental'noj fizikoj. Vo
vseh prevrashcheniyah takogo roda, izvestnyh pod nazvaniem _yadernye reakcii
zameshcheniya_, naletayushchaya chastica (proton, nejtron ili al'fa-chastica) pronikaet
v yadro, vybivaet kakuyu-to druguyu chasticu i ostaetsya na ee meste. Sushchestvuet
zameshchenie protona al'fa-chasticej, al'fa-chasticy protonom, protona nejtronom
i t.d. Vo vseh takih prevrashcheniyah novyj element, obrazovavshijsya v rezul'tate
reakcii, yavlyaetsya blizkim sosedom bombardiruemogo elementa v Periodicheskoj
sisteme.
No lish' sravnitel'no nedavno, pered vtoroj mirovoj vojnoj, dva nemeckih
himika O. Gan i F. SHtrassman otkryli sovershenno novyj tip yadernogo
prevrashcheniya, v kotorom _tyazheloe yadro raspadaetsya na dve ravnye poloviny s
vysvobozhdeniem ogromnogo kolichestva energii_. Na sleduyushchem slajde (sleduyushchij
slajd, pozhalujsta!) vy vidite (sm. s. 175) na snimke (B) dva oskolka yadra
urana, razletayushchihsya v raznye storony ot tonkoj uranovoj provolochki. |to
yavlenie, poluchivshee nazvanie _rasshcheplenie yadra_, vpervye nablyudalos' pri
bombardirovke urana puchkom nejtronov, no vskore fiziki obnaruzhili, chto i
drugie elementy, raspolozhennye v konce Periodicheskoj sistemy, obladayut
analogichnymi svojstvami. |ti tyazhelye yadra uzhe nahodyatsya u poroga svoej
stabil'nosti i malejshee vozmushchenie, vyzyvaemoe stolknoveniem s nejtronom,
dostatochno, chtoby oni raspalis' na dva oskolka, kak raspadaetsya na chasti
chrezmerno krupnaya kaplya rtuti. Nestabil'nost' tyazhelyh yader prolivaet svet na
vopros o tom, pochemu v prirode sushchestvuet tol'ko 92 elementa. Lyuboe yadro
tyazhelee urana ne mozhet sushchestvovat' skol'ko-nibud' prodolzhitel'noe vremya i
nemedlenno raspadaetsya na bolee melkie oskolki. YAvlenie rasshchepleniya yadra
predstavlyaet nemalyj interes i s prakticheskoj tochki zreniya, tak kak
otkryvaet opredelennye vozmozhnosti dlya ispol'zovaniya yadernoj energii. Delo v
tom, chto pri raspade yadra na dve polovinki iz yadra vyletaet neskol'ko
nejtronov, kotorye mogut vyzvat' rasshcheplenie sosednih yader. Dal'nejshee
rasprostranenie takogo processa mozhet privesti k vzryvnoj reakcii, pri
kotoroj vsya energiya, zapasennaya v yadrah, vysvobozhdaetsya za maluyu dolyu
sekundy. Esli vspomnit', chto yadernaya energiya, hranyashchayasya v odnom funte
urana, ekvivalentna energeticheskomu soderzhaniyu desyati tonn uglya, to stanet
yasno, chto vozmozhnost' vysvobozhdeniya yadernoj energii mogla by vyzvat'
glubokie peremeny v nashej ekonomike.

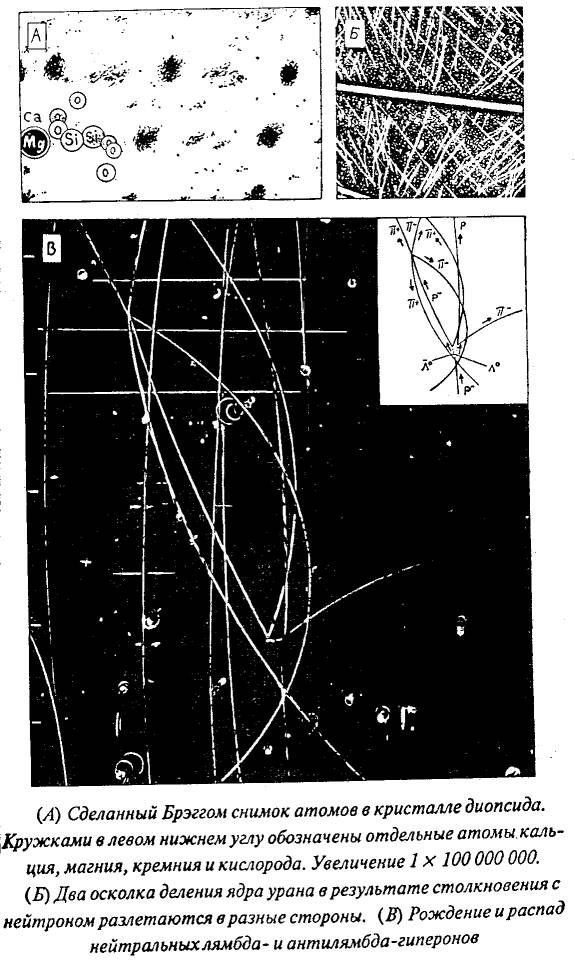 Odnako vse eti yadernye reakcii mogut byt' osushchestvleny lish' v ochen'
malom masshtabe, i, hotya oni pozvolyayut nam poluchit' bogatejshuyu informaciyu o
vnutrennem stroenii yadra, vplot' do sravnitel'no nedavnego vremeni ne bylo
ni malejshej nadezhdy na to, chto udastsya vysvobodit' ogromnoe kolichestvo
yadernoj energii. I lish' v 1939 g. nemeckie himiki O. Gan i F. SHtrassman
otkryli sovershenno novyj tip yadernogo prevrashcheniya: tyazheloe yadro urana pri
stolknovenii s odnim-edinstvennym nejtronom raspadaetsya na dve primerno
ravnye chasti s vysvobozhdeniem ogromnogo kolichestva energii i vyletom dvuh
ili treh nejtronov, kotorye v svoyu ochered' mogut stolknut'sya s yadrami urana
i rasshchepit' kazhdoe iz nih na dve chasti s vysvobozhdeniem novoj energii i
novyh nejtronov. Cepnoj process, deleniya yader urana mozhet privodit' k
vzryvam ili, esli sdelat' ego upravlyaemym, stat' pochti neischerpaemym
istochnikom energii. Schastliv soobshchit' vam, chto doktor Tallerkin, prinimavshij
uchastie v rabotah po sozdaniyu atomnoj bomby i izvestnyj takzhe kak otec
vodorodnoj bomby, lyubezno soglasilsya pribyt' k nam, nesmotrya na svoyu
chrezvychajnuyu zanyatost', i vystupit' s korotkim soobshcheniem o principah
ustrojstva yadernyh bomb. My ozhidaem ego pribytiya s minuty na minutu.
Edva professor uspel proiznesti eti slova, kak dver' otvorilas' i v
auditoriyu voshel chelovek ves'ma vnushitel'nogo vida s goryashchimi glazami i
navisshimi kustistymi brovyami. Obmenyavshis' s professorom rukopozhatiyami,
chelovek obratilsya k auditorii:
- Hoolgyeim es Uraim, - nachal on. - Roviden kell beszelnem, mert nagyon
sok a dolglom. Ma reggel tubb megbeszelesem volt a Pentagonban es a Feher
Hazban. Delutan... O, proshu proshcheniya! - voskliknul neznakomec. - Inogda ya
putayu yazyki. Pozvol'te mne nachat' eshche raz.
Ledi i dzhentl'meny! YA budu kratok, poskol'ku ochen' zanyat. Segodnya utrom
ya prisutstvoval na neskol'kih soveshchaniyah v Pentagone i v Belom dome, a dnem
mne neobhodimo byt' v French Flete, shtat Nevada, gde predstoit provesti
podzemnyj vzryv. Vecherom ya dolzhen proiznesti rech' na bankete, kotoryj
sostoitsya na baze VVS SSHA Vandenberg v Kalifornii.
Teper' o glavnom. Delo v tom, chto v atomnyh yadrah podderzhivaetsya
ravnovesie mezhdu silami dvoyakogo roda - yadernymi silami prityazheniya, kotorye
stremyatsya uderzhat' yadro v celosti, i elektricheskimi silami ottalkivaniya
mezhdu protonami. V tyazhelyh yadrah, takih kak yadra urana ili plutoniya, sily
ottalkivaniya preobladayut, i yadra pri malejshem vozmushchenii gotovy raspast'sya
na dva oskolka - produkty deleniya. Takim vozmushcheniem mozhet byt'
odin-edinstvennyj nejtron, stalkivayushchijsya s yadrom.
Obernuvshis' k doske, gost' prodolzhal:
- Vot delyashcheesya yadro, a vot stalkivayushchijsya s nim nejtron. Dva oskolka
deleniya razletayutsya v storony, i kazhdyj iz nih unosit okolo odnogo milliona
elektron-vol't energii. Krome togo, raspadayas', yadro vystrelilo neskol'kimi
novymi nejtronami deleniya (obychno ih byvaet dva v sluchae legkogo izotopa
urana i tri v sluchae plutoniya). Reakciya - bac, bac! - prodolzhaetsya, kak ya
izobrazil zdes' na doske. Esli kusok delyashchegosya materiala mal, to b_o_l'shaya
chast' nejtronov deleniya vyryvaetsya iz ego poverhnosti prezhde, chem oni imeyut
shans stolknut'sya s drugim delyashchimsya yadrom, i cepnaya reakciya tak i ne
nachinaetsya. No esli kusok delyashchegosya materiala imeet dostatochno bol'shie
razmery (my nazyvaem takoj kusok kriticheskoj massoj), dyujma tri-chetyre v
diametre, to bol'shinstvo nejtronov okazyvayutsya zahvachennymi, i vsya eta shtuka
vzryvaetsya. Takoe ustrojstvo my nazyvaem bomboj deleniya (v pechati ee
dovol'no chasto nepravil'no nazyvayut atomnoj bomboj).
Odnako vse eti yadernye reakcii mogut byt' osushchestvleny lish' v ochen'
malom masshtabe, i, hotya oni pozvolyayut nam poluchit' bogatejshuyu informaciyu o
vnutrennem stroenii yadra, vplot' do sravnitel'no nedavnego vremeni ne bylo
ni malejshej nadezhdy na to, chto udastsya vysvobodit' ogromnoe kolichestvo
yadernoj energii. I lish' v 1939 g. nemeckie himiki O. Gan i F. SHtrassman
otkryli sovershenno novyj tip yadernogo prevrashcheniya: tyazheloe yadro urana pri
stolknovenii s odnim-edinstvennym nejtronom raspadaetsya na dve primerno
ravnye chasti s vysvobozhdeniem ogromnogo kolichestva energii i vyletom dvuh
ili treh nejtronov, kotorye v svoyu ochered' mogut stolknut'sya s yadrami urana
i rasshchepit' kazhdoe iz nih na dve chasti s vysvobozhdeniem novoj energii i
novyh nejtronov. Cepnoj process, deleniya yader urana mozhet privodit' k
vzryvam ili, esli sdelat' ego upravlyaemym, stat' pochti neischerpaemym
istochnikom energii. Schastliv soobshchit' vam, chto doktor Tallerkin, prinimavshij
uchastie v rabotah po sozdaniyu atomnoj bomby i izvestnyj takzhe kak otec
vodorodnoj bomby, lyubezno soglasilsya pribyt' k nam, nesmotrya na svoyu
chrezvychajnuyu zanyatost', i vystupit' s korotkim soobshcheniem o principah
ustrojstva yadernyh bomb. My ozhidaem ego pribytiya s minuty na minutu.
Edva professor uspel proiznesti eti slova, kak dver' otvorilas' i v
auditoriyu voshel chelovek ves'ma vnushitel'nogo vida s goryashchimi glazami i
navisshimi kustistymi brovyami. Obmenyavshis' s professorom rukopozhatiyami,
chelovek obratilsya k auditorii:
- Hoolgyeim es Uraim, - nachal on. - Roviden kell beszelnem, mert nagyon
sok a dolglom. Ma reggel tubb megbeszelesem volt a Pentagonban es a Feher
Hazban. Delutan... O, proshu proshcheniya! - voskliknul neznakomec. - Inogda ya
putayu yazyki. Pozvol'te mne nachat' eshche raz.
Ledi i dzhentl'meny! YA budu kratok, poskol'ku ochen' zanyat. Segodnya utrom
ya prisutstvoval na neskol'kih soveshchaniyah v Pentagone i v Belom dome, a dnem
mne neobhodimo byt' v French Flete, shtat Nevada, gde predstoit provesti
podzemnyj vzryv. Vecherom ya dolzhen proiznesti rech' na bankete, kotoryj
sostoitsya na baze VVS SSHA Vandenberg v Kalifornii.
Teper' o glavnom. Delo v tom, chto v atomnyh yadrah podderzhivaetsya
ravnovesie mezhdu silami dvoyakogo roda - yadernymi silami prityazheniya, kotorye
stremyatsya uderzhat' yadro v celosti, i elektricheskimi silami ottalkivaniya
mezhdu protonami. V tyazhelyh yadrah, takih kak yadra urana ili plutoniya, sily
ottalkivaniya preobladayut, i yadra pri malejshem vozmushchenii gotovy raspast'sya
na dva oskolka - produkty deleniya. Takim vozmushcheniem mozhet byt'
odin-edinstvennyj nejtron, stalkivayushchijsya s yadrom.
Obernuvshis' k doske, gost' prodolzhal:
- Vot delyashcheesya yadro, a vot stalkivayushchijsya s nim nejtron. Dva oskolka
deleniya razletayutsya v storony, i kazhdyj iz nih unosit okolo odnogo milliona
elektron-vol't energii. Krome togo, raspadayas', yadro vystrelilo neskol'kimi
novymi nejtronami deleniya (obychno ih byvaet dva v sluchae legkogo izotopa
urana i tri v sluchae plutoniya). Reakciya - bac, bac! - prodolzhaetsya, kak ya
izobrazil zdes' na doske. Esli kusok delyashchegosya materiala mal, to b_o_l'shaya
chast' nejtronov deleniya vyryvaetsya iz ego poverhnosti prezhde, chem oni imeyut
shans stolknut'sya s drugim delyashchimsya yadrom, i cepnaya reakciya tak i ne
nachinaetsya. No esli kusok delyashchegosya materiala imeet dostatochno bol'shie
razmery (my nazyvaem takoj kusok kriticheskoj massoj), dyujma tri-chetyre v
diametre, to bol'shinstvo nejtronov okazyvayutsya zahvachennymi, i vsya eta shtuka
vzryvaetsya. Takoe ustrojstvo my nazyvaem bomboj deleniya (v pechati ee
dovol'no chasto nepravil'no nazyvayut atomnoj bomboj).
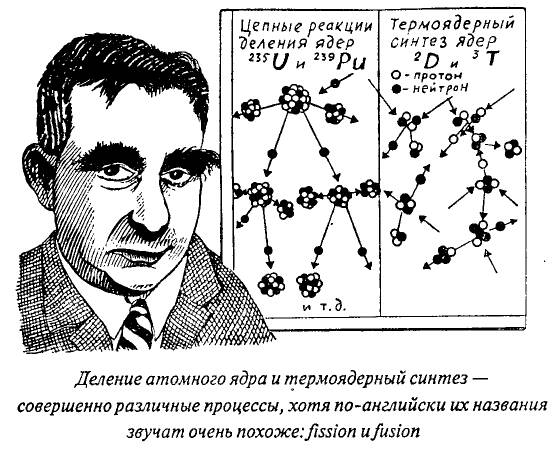 Gorazdo luchshih rezul'tatov mozhno dostich', esli obratit'sya k drugomu
koncu Periodicheskoj sistemy elementov, gde yadernye sily prevoshodyat
elektricheskoe ottalkivanie. Kogda dva legkih yadra prihodyat v
soprikosnovenie, oni slivayutsya, kak dve kapel'ki rtuti na blyudechke. Takoe
sliyanie mozhet proizojti tol'ko pri ochen' vysokoj temperature, tak kak
elektricheskoe ottalkivanie - meshaet legkim yadram sblizit'sya i prijti v
soprikosnovenie. No kogda temperatura dostigaet desyatkov millionov gradusov,
elektricheskoe ottalkivanie uzhe ne v silah pomeshat' sblizheniyu atomov i
process sliyaniya, ili termoyadernogo sinteza, nachinaetsya. Naibolee podhodyashchimi
yadrami dlya termoyadernogo sinteza yavlyayutsya dejtrony, t. e. yadra atomov
tyazhelogo vodoroda. Sprava na doske ya izobrazil prostuyu shemu termoyadernoj
reakcii v dejterii. Kogda my vpervye pridumali vodorodnuyu bombu, nam
kazalos', chto ona stanet blagosloveniem dlya vsego mira, tak kak pri ee
vzryve ne obrazuyutsya radioaktivnye produkty deleniya, kotorye potom
raznosyatsya po vsej zemnoj atmosfere. No nam ne udalos' sozdat' "chistuyu"
vodorodnuyu bombu, potomu chto dejterij, luchshee yadernoe toplivo, kotoroe legko
izvlekaetsya iz morskoj vody, nedostatochno horosho gorit sam po sebe. Nam
prishlos' okruzhit' dejterievuyu serdcevinu uranovoj obolochkoj. Takie obolochki
porozhdayut mnozhestvo oskolkov deleniya, i lyudi prozvali nashu konstrukciyu
"gryaznoj" vodorodnoj bomboj. Analogichnye trudnosti voznikli i pri
proektirovanii upravlyaemoj termoyadernoj reakcii s dejteriem i, nesmotrya na
vse usiliya, nam tak i ne udalos' osushchestvit' ee. No ya uveren, chto rano ili
pozdno problema upravlyaemogo termoyadernogo sinteza budet reshena.
- Doktor Tallerkin, - sprosil kto-to iz auditorii, - mogut li oskolki
deleniya yader pri ispytaniyah gryaznoj vodorodnoj bomby vyzvat' opasnye dlya
zdorov'ya cheloveka mutacii u naseleniya vsego zemnogo shara?
- Ne vse mutacii vredny, - ulybnulsya doktor Tallerkin. - Nekotorye
mutacii sposobstvuyut uluchsheniyu nasledstvennosti. Esli by v zhivyh organizmah
ne proishodili mutacii, to i vy, i ya vse eshche byli by amebami. Razve vy ne
znaete, chto evolyuciya zhizni na Zemle proishodit isklyuchitel'no blagodarya
mutaciyam i vyzhivaniyu naibolee prisposoblennyh mutantov?
- Uzh ne hotite li vy skazat', - istericheski zakrichala kakaya-to zhenshchina
v auditorii, - chto my dolzhny rozhat' detej dyuzhinami i, otobrav nailuchshih,
umervshchlyat' ostal'nyh?
- Vidite li... - nachal doktor Tallerkin, no v etot moment dver'
otvorilas' i v auditoriyu voshel chelovek v letnoj forme.
- Potoraplivajtes', ser! - skorogovorkoj dolozhil on. - Vash vertolet
priparkovan u vhoda i, esli my ne vyletim sejchas zhe, vy ne smozhete vovremya
pribyt' v aeroport, gde vas ozhidaet special'nyj reaktivnyj samolet!
- Proshu menya izvinit', - obratilsya doktor Tallerkin k auditorii, - no
mne pora idti. Isten veluk!
I oni oba, doktor Tallerkin i pilot, pospeshili iz auditorii.
Glava 13
Rezchik po derevu
Gorazdo luchshih rezul'tatov mozhno dostich', esli obratit'sya k drugomu
koncu Periodicheskoj sistemy elementov, gde yadernye sily prevoshodyat
elektricheskoe ottalkivanie. Kogda dva legkih yadra prihodyat v
soprikosnovenie, oni slivayutsya, kak dve kapel'ki rtuti na blyudechke. Takoe
sliyanie mozhet proizojti tol'ko pri ochen' vysokoj temperature, tak kak
elektricheskoe ottalkivanie - meshaet legkim yadram sblizit'sya i prijti v
soprikosnovenie. No kogda temperatura dostigaet desyatkov millionov gradusov,
elektricheskoe ottalkivanie uzhe ne v silah pomeshat' sblizheniyu atomov i
process sliyaniya, ili termoyadernogo sinteza, nachinaetsya. Naibolee podhodyashchimi
yadrami dlya termoyadernogo sinteza yavlyayutsya dejtrony, t. e. yadra atomov
tyazhelogo vodoroda. Sprava na doske ya izobrazil prostuyu shemu termoyadernoj
reakcii v dejterii. Kogda my vpervye pridumali vodorodnuyu bombu, nam
kazalos', chto ona stanet blagosloveniem dlya vsego mira, tak kak pri ee
vzryve ne obrazuyutsya radioaktivnye produkty deleniya, kotorye potom
raznosyatsya po vsej zemnoj atmosfere. No nam ne udalos' sozdat' "chistuyu"
vodorodnuyu bombu, potomu chto dejterij, luchshee yadernoe toplivo, kotoroe legko
izvlekaetsya iz morskoj vody, nedostatochno horosho gorit sam po sebe. Nam
prishlos' okruzhit' dejterievuyu serdcevinu uranovoj obolochkoj. Takie obolochki
porozhdayut mnozhestvo oskolkov deleniya, i lyudi prozvali nashu konstrukciyu
"gryaznoj" vodorodnoj bomboj. Analogichnye trudnosti voznikli i pri
proektirovanii upravlyaemoj termoyadernoj reakcii s dejteriem i, nesmotrya na
vse usiliya, nam tak i ne udalos' osushchestvit' ee. No ya uveren, chto rano ili
pozdno problema upravlyaemogo termoyadernogo sinteza budet reshena.
- Doktor Tallerkin, - sprosil kto-to iz auditorii, - mogut li oskolki
deleniya yader pri ispytaniyah gryaznoj vodorodnoj bomby vyzvat' opasnye dlya
zdorov'ya cheloveka mutacii u naseleniya vsego zemnogo shara?
- Ne vse mutacii vredny, - ulybnulsya doktor Tallerkin. - Nekotorye
mutacii sposobstvuyut uluchsheniyu nasledstvennosti. Esli by v zhivyh organizmah
ne proishodili mutacii, to i vy, i ya vse eshche byli by amebami. Razve vy ne
znaete, chto evolyuciya zhizni na Zemle proishodit isklyuchitel'no blagodarya
mutaciyam i vyzhivaniyu naibolee prisposoblennyh mutantov?
- Uzh ne hotite li vy skazat', - istericheski zakrichala kakaya-to zhenshchina
v auditorii, - chto my dolzhny rozhat' detej dyuzhinami i, otobrav nailuchshih,
umervshchlyat' ostal'nyh?
- Vidite li... - nachal doktor Tallerkin, no v etot moment dver'
otvorilas' i v auditoriyu voshel chelovek v letnoj forme.
- Potoraplivajtes', ser! - skorogovorkoj dolozhil on. - Vash vertolet
priparkovan u vhoda i, esli my ne vyletim sejchas zhe, vy ne smozhete vovremya
pribyt' v aeroport, gde vas ozhidaet special'nyj reaktivnyj samolet!
- Proshu menya izvinit', - obratilsya doktor Tallerkin k auditorii, - no
mne pora idti. Isten veluk!
I oni oba, doktor Tallerkin i pilot, pospeshili iz auditorii.
Glava 13
Rezchik po derevu
 Dver' byla bol'shaya i massivnaya. Posredine na nej krasovalas' nadpis',
sdelannaya krupnymi bukvami: "Ostorozhno! Vysokoe napryazhenie!". No pervoe
vpechatlenie negostepriimstva neskol'ko smyagchalos' krupnoj nadpis'yu "Dobro
pozhalovat'!" na kovrike u dveri, i posle minutnogo kolebaniya mister Tompkins
nazhal na knopku dvernogo zvonka. Dver' otkryl molodoj assistent, i mister
Tompkins okazalsya v ogromnom pomeshchenii, dobruyu polovinu kotorogo zanimala
zamyslovataya mashina samogo fantasticheskogo vida.
- |to nash ciklotron, ili "atomnaya drobilka", kak ego nazyvayut v
gazetah, - poyasnil assistent, lyubovno poglazhivaya vitki odnoj iz katushek
gigantskogo elektromagnita, sostavlyayushchego osnovnuyu chast' ves'ma vnushitel'no
vyglyadevshego orudiya sovremennoj fiziki.
- On pozvolyaet poluchat' chasticy s energiej do desyati millionov
elektron-vol't, - s gordost'yu prodolzhal assistent, - i nemnogo najdetsya
yader, kotorye sposobny vyderzhat' stolknovenie s chasticej, dvizhushchejsya s takoj
nevoobrazimoj energiej!
- Potryasayushche interesno! - otozvalsya mister Tompkins. - |ti yadra, dolzhno
byt', ochen' prochny! Trudno poverit', chto etakaya mahina byla postroena tol'ko
dlya togo, chtoby raskololos' krohotnoe yadro krohotnogo atoma. A kak rabotaet
eta mashina?
- Vy byli kogda-nibud' v cirke? - sprosil mistera Tompkinsa ego test',
vnezapno voznikaya otkuda-to iz-za gigantskogo ciklotrona.
- Razumeetsya, byl, - otvetil mister Tompkins, neskol'ko udivlennyj
neozhidannym voprosom. - Vy hotite predlozhit' mne pojti s vami segodnya v cirk
na vechernee predstavlenie?
- Ne sovsem, - ulybnulsya professor. - Prosto, esli vam sluchalos' byvat'
v cirke, eto pomozhet vam ponyat', kak rabotaet ciklotron. Vzglyanite mezhdu
polyusov etogo ogromnogo magnita i vy uvidite kruglyj mednyj kozhuh. On sluzhit
kol'com, v kotorom uskoryayutsya razlichnye zaryazhennye chasticy, ispol'zuemye v
eksperimentah po bombardirovke yader. V centre kozhuha raspolozhen istochnik,
ispuskayushchij vse eti zaryazhennye chasticy, ili iony. Vyletaya iz istochnika, iony
dvizhutsya s ochen' malen'kimi skorostyami, i sil'noe pole, sozdavaemoe
magnitom, izgibaet ih traektorii v nebol'shie okruzhnosti vokrug centra. Zatem
my nachinaem pogonyat' chasticy i razgonyaem ih do vse bol'shih i bol'shih
skorostej.
- YA ponimayu, kak pogonyat' loshad', - zametil mister Tompkins, - no kak
vam udaetsya pogonyat' krohotnye zaryazhennye chasticy, vyshe moego razumeniya.
- A mezhdu tem eto ochen' prosto. Esli chastica dvizhetsya po krugu, to vse,
chto neobhodimo delat', eto soobshchat' ej ryad posledovatel'nyh elektricheskih
tolchkov vsyakij raz, kogda chastica budet prohodit' cherez opredelennuyu tochku
svoej traektorii, podobno tomu, kak v cirke trener hlystom podgonyaet loshad'
vsyakij raz, kogda ta, opisyvaya po arene krug za krugom, probegaet mimo nego.
Dver' byla bol'shaya i massivnaya. Posredine na nej krasovalas' nadpis',
sdelannaya krupnymi bukvami: "Ostorozhno! Vysokoe napryazhenie!". No pervoe
vpechatlenie negostepriimstva neskol'ko smyagchalos' krupnoj nadpis'yu "Dobro
pozhalovat'!" na kovrike u dveri, i posle minutnogo kolebaniya mister Tompkins
nazhal na knopku dvernogo zvonka. Dver' otkryl molodoj assistent, i mister
Tompkins okazalsya v ogromnom pomeshchenii, dobruyu polovinu kotorogo zanimala
zamyslovataya mashina samogo fantasticheskogo vida.
- |to nash ciklotron, ili "atomnaya drobilka", kak ego nazyvayut v
gazetah, - poyasnil assistent, lyubovno poglazhivaya vitki odnoj iz katushek
gigantskogo elektromagnita, sostavlyayushchego osnovnuyu chast' ves'ma vnushitel'no
vyglyadevshego orudiya sovremennoj fiziki.
- On pozvolyaet poluchat' chasticy s energiej do desyati millionov
elektron-vol't, - s gordost'yu prodolzhal assistent, - i nemnogo najdetsya
yader, kotorye sposobny vyderzhat' stolknovenie s chasticej, dvizhushchejsya s takoj
nevoobrazimoj energiej!
- Potryasayushche interesno! - otozvalsya mister Tompkins. - |ti yadra, dolzhno
byt', ochen' prochny! Trudno poverit', chto etakaya mahina byla postroena tol'ko
dlya togo, chtoby raskololos' krohotnoe yadro krohotnogo atoma. A kak rabotaet
eta mashina?
- Vy byli kogda-nibud' v cirke? - sprosil mistera Tompkinsa ego test',
vnezapno voznikaya otkuda-to iz-za gigantskogo ciklotrona.
- Razumeetsya, byl, - otvetil mister Tompkins, neskol'ko udivlennyj
neozhidannym voprosom. - Vy hotite predlozhit' mne pojti s vami segodnya v cirk
na vechernee predstavlenie?
- Ne sovsem, - ulybnulsya professor. - Prosto, esli vam sluchalos' byvat'
v cirke, eto pomozhet vam ponyat', kak rabotaet ciklotron. Vzglyanite mezhdu
polyusov etogo ogromnogo magnita i vy uvidite kruglyj mednyj kozhuh. On sluzhit
kol'com, v kotorom uskoryayutsya razlichnye zaryazhennye chasticy, ispol'zuemye v
eksperimentah po bombardirovke yader. V centre kozhuha raspolozhen istochnik,
ispuskayushchij vse eti zaryazhennye chasticy, ili iony. Vyletaya iz istochnika, iony
dvizhutsya s ochen' malen'kimi skorostyami, i sil'noe pole, sozdavaemoe
magnitom, izgibaet ih traektorii v nebol'shie okruzhnosti vokrug centra. Zatem
my nachinaem pogonyat' chasticy i razgonyaem ih do vse bol'shih i bol'shih
skorostej.
- YA ponimayu, kak pogonyat' loshad', - zametil mister Tompkins, - no kak
vam udaetsya pogonyat' krohotnye zaryazhennye chasticy, vyshe moego razumeniya.
- A mezhdu tem eto ochen' prosto. Esli chastica dvizhetsya po krugu, to vse,
chto neobhodimo delat', eto soobshchat' ej ryad posledovatel'nyh elektricheskih
tolchkov vsyakij raz, kogda chastica budet prohodit' cherez opredelennuyu tochku
svoej traektorii, podobno tomu, kak v cirke trener hlystom podgonyaet loshad'
vsyakij raz, kogda ta, opisyvaya po arene krug za krugom, probegaet mimo nego.
 - No trener vidit loshad', - vozrazil mister Tompkins. - A razve vy
vidite chasticu, opisyvayushchuyu krug za krugom v toj mednoj korobke, chtoby
podtolknut' ee v nuzhnyj moment?
- Razumeetsya, ne vizhu, - soglasilsya professor, - no eto i
neobyazatel'no. Vsya hitrost' ustrojstva ciklotrona sostoit v tom, chto, hotya
uskoryaemaya chastica dvizhetsya vse bystree i bystree, ona vsegda sovershaet
polnyj oborot za odno i to zhe vremya. Delo v tom, chto po mere uvelicheniya
skorosti chasticy radius, a sledovatel'no, i dlina ee krugovoj traektorii
takzhe sootvetstvenno uvelichivayutsya. V rezul'tate uskoryaemaya chastica dvizhetsya
po raskruchivayushchejsya spirali i vsegda prihodit v odno i to zhe mesto "kol'ca"
cherez odinakovye promezhutki vremeni. Vse, chto neobhodimo sdelat', eto
pomestit' v dannom meste kakoe-nibud' elektricheskoe ustrojstvo, kotoroe
podtalkivalo by chasticu cherez odinakovye promezhutki vremeni. My delaem eto s
pomoshch'yu kolebatel'nogo elektricheskogo kontura, ochen' pohozhego na te shemy,
kotorye vy mozhete videt' na lyuboj radiostancii. Kazhdyj elektricheskij tolchok
ne ochen' silen, no kumulyativnyj effekt mnogih tolchkov pozvolyaet razgonyat'
chasticu do ochen' bol'shih skorostej. V etom ogromnoe preimushchestvo ciklotrona:
on pozvolyaet dostigat' takogo zhe effekta, kak napryazhenie vo mnogie milliony
vol't, hotya nigde v ciklotrone vy ne najdete vysokih napryazhenij.
- Ochen' ostroumno, - zadumchivo proiznes mister Tompkins, - A ch'e eto
izobretenie?
- Pervyj ciklotron byl postroen neskol'ko let nazad nyne pokojnym
|rnestom Orlando Lourensom v Kalifornijskom universitete, - otvetil
professor. - S teh por ciklotrony znachitel'no vyrosli v svoih razmerah i
rasprostranilis' po fizicheskim laboratoriyam so skorost'yu sluhov. Oni
okazalis' udobnee, chem starye uskoriteli s celym kaskadom transformatorov
ili drugie uskoriteli, rabotavshie kak elektrostaticheskie mashiny.
- A nel'zya li razbit' atomnoe yadro vdrebezgi, ne pribegaya ko vsem etim
slozhnym mashinam? - sprosil mister Tompkins, tverdo ubezhdennyj storonnik
prostoty, s nedoveriem otnosivshijsya k lyubym ustrojstvam slozhnee molotka.
- Razumeetsya, mozhno. Kogda Rezerford provodil svoi pervye eksperimenty
po iskusstvennomu prevrashcheniyu elementov, on kak raz ispol'zoval obychnye
al'fa-chasticy, ispuskaemye estestvennymi radioaktivnymi istochnikami. No eto
bylo bolee dvadcati let nazad, i, kak vy mozhete ubedit'sya, s teh por metody
deleniya atoma sushchestvenno usovershenstvovalis'.
- A ne mozhete li vy pokazat' mne, kak razbivayut atom? - poprosil mister
Tompkins, vsegda predpochitavshij uvidet' svoimi glazami vmesto togo, chtoby
vyslushivat' dlinnye ob座asneniya.
- S udovol'stviem, - otvetil professor. - My kak raz pristupaem k
eksperimentu po dal'nejshemu issledovaniyu deleniya yadra bora pri stolknovenii
s bystrymi protonami. Kogda yadro bora stalkivaetsya s protonom i eto
stolknovenie dostatochno sil'no dlya togo, chtoby bombardiruyushchaya chastica
pronikla skvoz' potencial'nyj bar'er i okazalas' vnutri yadra, ono
raspadaetsya na tri primerno ravnyh oskolka, kotorye razletayutsya vo vse
storony. Ves' process mozhno nablyudat' neposredstvenno v tak nazyvaemoj
puzyr'kovoj kamere, delayushchej vidimymi traektorii vseh chastic, uchastvuyushchih v
stolknovenii. Takaya kamera s nebol'shim kusochkom bora v seredine ustanovlena
u vyhoda uskoritel'noj sistemy, i kak tol'ko ciklotron zarabotaet, vy
uvidite delenie yadra sobstvennymi glazami.
- Vklyuchite, pozhalujsta, tok, - obratilsya professor k svoemu assistentu,
- a ya poka zajmus' regulirovkoj magnitnogo polya.
CHtoby zapustit' ciklotron, ponadobilos' nekotoroe vremya, i
predostavlennyj samomu sebe mister Tompkins prazdno brodil po laboratorii.
Ego vnimanie privlekla slozhnaya sistema usilitel'nyh lamp, tlevshih slabym
golubovatym svetom. Ne znaya v tochnosti, kakie elektricheskie napryazheniya
ispol'zuyutsya v ciklotrone (napryazhenie mozhet byt' malo dlya togo, chtoby
rasshchepit' atomnoe yadro, no vpolne dostatochno, chtoby svalit' byka!), mister
Tompkins ostorozhno naklonilsya nad lampami.
Posledoval rezkij shchelchok, slovno ukrotitel' l'vov vzmahnul svoim
hlystom, i mister Tompkins pochuvstvoval uzhasnuyu bol', pronzivshuyu vse ego
telo. V tot zhe mig t'ma okutala vse, i on poteryal soznanie.
Kogda mister Tompkins, nakonec, otkryl glaza, on obnaruzhil, chto lezhit
na polu v tom samom meste, gde ego srazil elektricheskij razryad. Pomeshchenie
vrode by ostavalos' prezhnim, no bylo obstavleno sovershenno po-drugomu.
Vmesto vozvyshavshegosya napodobie bashni ciklotronnogo magnita, siyayushchih mednyh
kontaktov i desyatkov slozhnyh elektricheskih ustrojstv, torchavshih tut i tam,
mister Tompkins uvidel derevyannyj stol, na kotorom byli razbrosany
plotnickie instrumenty. Na staromodnyh polkah, visevshih po stenam, mister
Tompkins zametil mnozhestvo vyrezannyh iz dereva figur strannyh i neobychnyh
form. Za stolom sidel privetlivyj starichok. Priglyadevshis' k ego chertam,
mister Tompkins byl porazhen sil'nym shodstvom so starikom Dzhepetto iz fil'ma
"Pinokkio" Uolta Disneya i s portretom pokojnogo Rezerforda lorda Nel'sona,
visevshim v laboratorii u professora.
- Proshu proshcheniya za nevol'noe vtorzhenie, - skazal mister Tompkins,
podnimayas' s pola. - Vidite li, ya byl na ekskursii v yadernoj laboratorii i
tam so mnoj priklyuchilos' chto-to strannoe.
- A, tak vy interesuetes' atomnym yadrom? - ozhivilsya starichok,
otkladyvaya v storonu derevyannuyu figurku, kotoruyu on vyrezal. Togda vy popali
kak raz tuda, kuda nado! YA izgotovlyayu vsevozmozhnye yadra i budu rad pokazat'
vam svoyu masterskuyu.
- YA ne oslyshalsya? - peresprosil mister Tompkins s ozadachennym vidom. -
Vy skazali, chto zanimaetes' izgotovleniem yader?
- Da, vy ne oslyshalis'. Pravda, eto trebuet izvestnoj snorovki, v
osobennosti izgotovlenie radioaktivnyh yader. Ved' ne uspeesh' ih vykrasit',
kak oni mogut raspast'sya.
- _Vykrasit'_?
- Da, polozhitel'no zaryazhennye chasticy ya obychno okrashivayu v krasnyj
cvet, a otricatel'no zaryazhennye - v zelenyj. Vy, dolzhno byt', znaete, chto
krasnyj i zelenyj cveta prinadlezhat k chislu tak nazyvaemyh _dopolnitel'nyh
cvetov_ i pri smeshivanii unichtozhayut drug druga {CHitatel' dolzhen imet' v
vidu, chto, govorya o smeshivanii cvetov, my imeem v vidu tol'ko luchi sveta
sootvetstvuyushchej okraski, a ne sami cveta. Esli smeshat' krasnuyu i zelenuyu
kraski, to poluchitsya nekij gryaznyj cvet. Esli zhe polovinu verhnej storony
volchka vykrasit' v krasnyj cvet, a druguyu polovinu - v zelenyj, to, zakrutiv
volchok, my uvidim, chto on belyj.}. Dopolnitel'nye cveta sootvetstvuyut
polozhitel'nym i otricatel'nym elektricheskim zaryadam, kotorye nejtralizuyut
drug druga. Esli atomnoe yadro sostoit iz odinakovogo chisla polozhitel'nyh i
otricatel'nyh zaryadov, bystro dvigayushchihsya v odnu i v druguyu storonu, to
takoe yadro budet elektricheski nejtral'nym i pokazhetsya vam belym. Esli zhe
polozhitel'nyh ili otricatel'nyh chastic budet bol'she, to vsya sistema budet
okrashena v krasnyj ili v zelenyj cvet. Ne pravda li, prosto?
- Zdes', - prodolzhal starichok, pokazyvaya misteru Tompkinsu dva bol'shih
derevyannyh yashchika, stoyavshih vozle stola, - ya hranyu materialy, iz kotoryh
mozhno izgotovit' razlichnye yadra. V pervom yashchike u menya hranyatsya _protony_ -
vidite eti krasnye shary? Oni ochen' stabil'ny i sohranyayut svoj krasnyj cvet,
dazhe esli vy vzdumaete poskoblit' ih nozhom ili chem-nibud' pocarapat'. S
_nejtronami_ vo vtorom yashchike hlopot gorazdo bol'she. Obychno oni belye, ili
elektricheski nejtral'nye, no obnaruzhivayut sil'nuyu tendenciyu prevrashchat'sya v
krasnye protony. Poka yashchik plotno zakryt, vse v poryadke, no stoit lish'
vynut' odin nejtron iz yashchika, kak proishodit sleduyushchee. Vot, polyubujtes'
sami.
Otkryv yashchik, staryj rezchik po derevu izvlek iz nego odin iz belyh sharov
i polozhil ego na stol. Kakoe-to vremya nichego ne proishodilo, no kak raz v
tot moment, kogda mister Tompkins nachal teryat' terpenie, shar vnezapno ozhil.
Na ego poverhnosti poyavilis' krasnovatye i zelenovatye polosy, i vskore
nekogda belyj shar vyglyadel, kak odin iz teh pestryh mramornyh sharikov, v
kotorye tak lyubyat igrat' deti. Zelenyj cvet nachal koncentrirovat'sya na odnoj
storone shara, kotoraya nachala vypyachivat'sya i zatem polnost'yu otdelilas' ot
shara, obrazovav blestyashchuyu zelenuyu kaplyu, kotoraya upala na pol. SHar posle
etogo stal krasnym i po vneshnemu vidu nichem ne otlichalsya ot krasnyh
sharov-protonov v pervom yashchike.
- No trener vidit loshad', - vozrazil mister Tompkins. - A razve vy
vidite chasticu, opisyvayushchuyu krug za krugom v toj mednoj korobke, chtoby
podtolknut' ee v nuzhnyj moment?
- Razumeetsya, ne vizhu, - soglasilsya professor, - no eto i
neobyazatel'no. Vsya hitrost' ustrojstva ciklotrona sostoit v tom, chto, hotya
uskoryaemaya chastica dvizhetsya vse bystree i bystree, ona vsegda sovershaet
polnyj oborot za odno i to zhe vremya. Delo v tom, chto po mere uvelicheniya
skorosti chasticy radius, a sledovatel'no, i dlina ee krugovoj traektorii
takzhe sootvetstvenno uvelichivayutsya. V rezul'tate uskoryaemaya chastica dvizhetsya
po raskruchivayushchejsya spirali i vsegda prihodit v odno i to zhe mesto "kol'ca"
cherez odinakovye promezhutki vremeni. Vse, chto neobhodimo sdelat', eto
pomestit' v dannom meste kakoe-nibud' elektricheskoe ustrojstvo, kotoroe
podtalkivalo by chasticu cherez odinakovye promezhutki vremeni. My delaem eto s
pomoshch'yu kolebatel'nogo elektricheskogo kontura, ochen' pohozhego na te shemy,
kotorye vy mozhete videt' na lyuboj radiostancii. Kazhdyj elektricheskij tolchok
ne ochen' silen, no kumulyativnyj effekt mnogih tolchkov pozvolyaet razgonyat'
chasticu do ochen' bol'shih skorostej. V etom ogromnoe preimushchestvo ciklotrona:
on pozvolyaet dostigat' takogo zhe effekta, kak napryazhenie vo mnogie milliony
vol't, hotya nigde v ciklotrone vy ne najdete vysokih napryazhenij.
- Ochen' ostroumno, - zadumchivo proiznes mister Tompkins, - A ch'e eto
izobretenie?
- Pervyj ciklotron byl postroen neskol'ko let nazad nyne pokojnym
|rnestom Orlando Lourensom v Kalifornijskom universitete, - otvetil
professor. - S teh por ciklotrony znachitel'no vyrosli v svoih razmerah i
rasprostranilis' po fizicheskim laboratoriyam so skorost'yu sluhov. Oni
okazalis' udobnee, chem starye uskoriteli s celym kaskadom transformatorov
ili drugie uskoriteli, rabotavshie kak elektrostaticheskie mashiny.
- A nel'zya li razbit' atomnoe yadro vdrebezgi, ne pribegaya ko vsem etim
slozhnym mashinam? - sprosil mister Tompkins, tverdo ubezhdennyj storonnik
prostoty, s nedoveriem otnosivshijsya k lyubym ustrojstvam slozhnee molotka.
- Razumeetsya, mozhno. Kogda Rezerford provodil svoi pervye eksperimenty
po iskusstvennomu prevrashcheniyu elementov, on kak raz ispol'zoval obychnye
al'fa-chasticy, ispuskaemye estestvennymi radioaktivnymi istochnikami. No eto
bylo bolee dvadcati let nazad, i, kak vy mozhete ubedit'sya, s teh por metody
deleniya atoma sushchestvenno usovershenstvovalis'.
- A ne mozhete li vy pokazat' mne, kak razbivayut atom? - poprosil mister
Tompkins, vsegda predpochitavshij uvidet' svoimi glazami vmesto togo, chtoby
vyslushivat' dlinnye ob座asneniya.
- S udovol'stviem, - otvetil professor. - My kak raz pristupaem k
eksperimentu po dal'nejshemu issledovaniyu deleniya yadra bora pri stolknovenii
s bystrymi protonami. Kogda yadro bora stalkivaetsya s protonom i eto
stolknovenie dostatochno sil'no dlya togo, chtoby bombardiruyushchaya chastica
pronikla skvoz' potencial'nyj bar'er i okazalas' vnutri yadra, ono
raspadaetsya na tri primerno ravnyh oskolka, kotorye razletayutsya vo vse
storony. Ves' process mozhno nablyudat' neposredstvenno v tak nazyvaemoj
puzyr'kovoj kamere, delayushchej vidimymi traektorii vseh chastic, uchastvuyushchih v
stolknovenii. Takaya kamera s nebol'shim kusochkom bora v seredine ustanovlena
u vyhoda uskoritel'noj sistemy, i kak tol'ko ciklotron zarabotaet, vy
uvidite delenie yadra sobstvennymi glazami.
- Vklyuchite, pozhalujsta, tok, - obratilsya professor k svoemu assistentu,
- a ya poka zajmus' regulirovkoj magnitnogo polya.
CHtoby zapustit' ciklotron, ponadobilos' nekotoroe vremya, i
predostavlennyj samomu sebe mister Tompkins prazdno brodil po laboratorii.
Ego vnimanie privlekla slozhnaya sistema usilitel'nyh lamp, tlevshih slabym
golubovatym svetom. Ne znaya v tochnosti, kakie elektricheskie napryazheniya
ispol'zuyutsya v ciklotrone (napryazhenie mozhet byt' malo dlya togo, chtoby
rasshchepit' atomnoe yadro, no vpolne dostatochno, chtoby svalit' byka!), mister
Tompkins ostorozhno naklonilsya nad lampami.
Posledoval rezkij shchelchok, slovno ukrotitel' l'vov vzmahnul svoim
hlystom, i mister Tompkins pochuvstvoval uzhasnuyu bol', pronzivshuyu vse ego
telo. V tot zhe mig t'ma okutala vse, i on poteryal soznanie.
Kogda mister Tompkins, nakonec, otkryl glaza, on obnaruzhil, chto lezhit
na polu v tom samom meste, gde ego srazil elektricheskij razryad. Pomeshchenie
vrode by ostavalos' prezhnim, no bylo obstavleno sovershenno po-drugomu.
Vmesto vozvyshavshegosya napodobie bashni ciklotronnogo magnita, siyayushchih mednyh
kontaktov i desyatkov slozhnyh elektricheskih ustrojstv, torchavshih tut i tam,
mister Tompkins uvidel derevyannyj stol, na kotorom byli razbrosany
plotnickie instrumenty. Na staromodnyh polkah, visevshih po stenam, mister
Tompkins zametil mnozhestvo vyrezannyh iz dereva figur strannyh i neobychnyh
form. Za stolom sidel privetlivyj starichok. Priglyadevshis' k ego chertam,
mister Tompkins byl porazhen sil'nym shodstvom so starikom Dzhepetto iz fil'ma
"Pinokkio" Uolta Disneya i s portretom pokojnogo Rezerforda lorda Nel'sona,
visevshim v laboratorii u professora.
- Proshu proshcheniya za nevol'noe vtorzhenie, - skazal mister Tompkins,
podnimayas' s pola. - Vidite li, ya byl na ekskursii v yadernoj laboratorii i
tam so mnoj priklyuchilos' chto-to strannoe.
- A, tak vy interesuetes' atomnym yadrom? - ozhivilsya starichok,
otkladyvaya v storonu derevyannuyu figurku, kotoruyu on vyrezal. Togda vy popali
kak raz tuda, kuda nado! YA izgotovlyayu vsevozmozhnye yadra i budu rad pokazat'
vam svoyu masterskuyu.
- YA ne oslyshalsya? - peresprosil mister Tompkins s ozadachennym vidom. -
Vy skazali, chto zanimaetes' izgotovleniem yader?
- Da, vy ne oslyshalis'. Pravda, eto trebuet izvestnoj snorovki, v
osobennosti izgotovlenie radioaktivnyh yader. Ved' ne uspeesh' ih vykrasit',
kak oni mogut raspast'sya.
- _Vykrasit'_?
- Da, polozhitel'no zaryazhennye chasticy ya obychno okrashivayu v krasnyj
cvet, a otricatel'no zaryazhennye - v zelenyj. Vy, dolzhno byt', znaete, chto
krasnyj i zelenyj cveta prinadlezhat k chislu tak nazyvaemyh _dopolnitel'nyh
cvetov_ i pri smeshivanii unichtozhayut drug druga {CHitatel' dolzhen imet' v
vidu, chto, govorya o smeshivanii cvetov, my imeem v vidu tol'ko luchi sveta
sootvetstvuyushchej okraski, a ne sami cveta. Esli smeshat' krasnuyu i zelenuyu
kraski, to poluchitsya nekij gryaznyj cvet. Esli zhe polovinu verhnej storony
volchka vykrasit' v krasnyj cvet, a druguyu polovinu - v zelenyj, to, zakrutiv
volchok, my uvidim, chto on belyj.}. Dopolnitel'nye cveta sootvetstvuyut
polozhitel'nym i otricatel'nym elektricheskim zaryadam, kotorye nejtralizuyut
drug druga. Esli atomnoe yadro sostoit iz odinakovogo chisla polozhitel'nyh i
otricatel'nyh zaryadov, bystro dvigayushchihsya v odnu i v druguyu storonu, to
takoe yadro budet elektricheski nejtral'nym i pokazhetsya vam belym. Esli zhe
polozhitel'nyh ili otricatel'nyh chastic budet bol'she, to vsya sistema budet
okrashena v krasnyj ili v zelenyj cvet. Ne pravda li, prosto?
- Zdes', - prodolzhal starichok, pokazyvaya misteru Tompkinsu dva bol'shih
derevyannyh yashchika, stoyavshih vozle stola, - ya hranyu materialy, iz kotoryh
mozhno izgotovit' razlichnye yadra. V pervom yashchike u menya hranyatsya _protony_ -
vidite eti krasnye shary? Oni ochen' stabil'ny i sohranyayut svoj krasnyj cvet,
dazhe esli vy vzdumaete poskoblit' ih nozhom ili chem-nibud' pocarapat'. S
_nejtronami_ vo vtorom yashchike hlopot gorazdo bol'she. Obychno oni belye, ili
elektricheski nejtral'nye, no obnaruzhivayut sil'nuyu tendenciyu prevrashchat'sya v
krasnye protony. Poka yashchik plotno zakryt, vse v poryadke, no stoit lish'
vynut' odin nejtron iz yashchika, kak proishodit sleduyushchee. Vot, polyubujtes'
sami.
Otkryv yashchik, staryj rezchik po derevu izvlek iz nego odin iz belyh sharov
i polozhil ego na stol. Kakoe-to vremya nichego ne proishodilo, no kak raz v
tot moment, kogda mister Tompkins nachal teryat' terpenie, shar vnezapno ozhil.
Na ego poverhnosti poyavilis' krasnovatye i zelenovatye polosy, i vskore
nekogda belyj shar vyglyadel, kak odin iz teh pestryh mramornyh sharikov, v
kotorye tak lyubyat igrat' deti. Zelenyj cvet nachal koncentrirovat'sya na odnoj
storone shara, kotoraya nachala vypyachivat'sya i zatem polnost'yu otdelilas' ot
shara, obrazovav blestyashchuyu zelenuyu kaplyu, kotoraya upala na pol. SHar posle
etogo stal krasnym i po vneshnemu vidu nichem ne otlichalsya ot krasnyh
sharov-protonov v pervom yashchike.
 - Vidite, chto proishodit, - skazal rezchik, podnimaya s pola zelenuyu
kaplyu, stavshuyu tverdoj i krugloj. - Belyj cvet nejtrona prevratilsya v
zelenyj i krasnyj, a sam nejtron raspalsya na dve otdel'nye chasticy - proton
i otricatel'no zaryazhennyj elektron.
- Vidite, chto proishodit, - skazal rezchik, podnimaya s pola zelenuyu
kaplyu, stavshuyu tverdoj i krugloj. - Belyj cvet nejtrona prevratilsya v
zelenyj i krasnyj, a sam nejtron raspalsya na dve otdel'nye chasticy - proton
i otricatel'no zaryazhennyj elektron.
 - Da, da, - dobavil starichok, vidya izumlennoe vyrazhenie na lice mistera
Tompkinsa, - eta chastica cveta nefrita - ne chto inoe, kak obyknovennyj
elektron, nichem ne otlichayushchijsya ot drugih elektronov v lyubom atome i v chem
ugodno.
- Podumat' tol'ko! - voskliknul mister Tompkins. - |to dejstvitel'no
prevoshodit vse fokusy s raznocvetnymi nosovymi platkami, kakie tol'ko mne
prihodilos' videt'. A mozhete li vy vernut' sharam ih ishodnuyu okrasku?
- Da, ya votru zelenuyu krasku v poverhnost' krasnogo shara, ot chego shar
snova stanet belym. Razumeetsya, dlya etogo pridetsya zatratit' opredelennoe
kolichestvo energii. Drugoj sposob sostoit v tom, chtoby soskresti s shara
krasnuyu krasku, no i on trebuet zatrat energii. Soskoblennaya s poverhnosti
protona krasnaya kraska obrazuet krasnuyu kaplyu, t. e. polozhitel'no zaryazhennyj
elektron, o kotorom vam, dolzhno byt', prihodilos' slyshat'.
- O da, kogda ya byl elektronom, - nachal bylo mister Tompkins, no vo
vremya spohvatilsya, - t. e. ya hochu skazat', chto slyshal, budto polozhitel'nye i
otricatel'nye elektrony pri stolknovenii annigiliruyut, t. e. vzaimno
unichtozhayutsya. Ne mogli by vy prodelat' etot tryuk dlya menya?
- S udovol'stviem, - otvetil staryj master. - Delaetsya eto ochen'
prosto. YA ne stanu soskrebat' krasku s etogo protona. U menya i tak ostalas'
parochka-drugaya protonov ot utrennej raboty.
Otkryv odin iz yashchikov, on izvlek iz nego nebol'shoj yarko-krasnyj shar i,
krepko derzha ego mezhdu ukazatel'nym i bol'shim pal'cami, prizhal k zelenomu
sharu, lezhavshemu na stole. Posledoval gromkij tresk, slovno vzorvalas'
hlopushka, i oba shara odnovremenno ischezli.
- Videli? - sprosil rezchik, duya na slegka obozhzhennye pal'cy. - Poetomu
iz elektronov i nel'zya stroit' yadra. Odnazhdy ya popytalsya, no potom brosil
etu zateyu i teper' stroyu yadra tol'ko iz protonov i nejtronov.
- No ved' nejtrony tozhe nestabil'ny, esli ya ne oshibayus'? - sprosil
mister Tompkins, vspominaya prevrashcheniya belogo shara.
- Esli brat' nejtrony poodinochke, to oni dejstvitel'no nestabil'ny. No
kogda oni plotno upakovany v yadre i okruzheny drugimi chasticami, to
stanovyatsya stabil'nymi. Esli zhe nejtronov ili protonov stanovitsya slishkom
mnogo, to oni mogut preterpevat' prevrashcheniya i ispuskat' iz yadra lishnyuyu
krasku v vide polozhitel'no ili otricatel'no zaryazhennyh elektronov. Takie
sobytiya my nazyvaem beta-raspadom.
- Ispol'zuete li vy pri izgotovlenii yader klej? - pointeresovalsya
mister Tompkins.
- Net, nikakoj klej mne ne nuzhen, - otvetil staryj master. - |ti
chasticy, izvol'te videt', sami slipayutsya, stoit lish' podnesti ih drug k
drugu. Poprobujte sami, esli hotite.
Posledovav etomu lyubeznomu priglasheniyu, mister Tompkins vzyal v odnu
ruku proton, v druguyu nejtron i ostorozhno nachal ih sblizhat'. On srazu zhe
pochuvstvoval sil'noe prityazhenie i, vzglyanuv na chasticy, zametil chrezvychajno
strannoe yavlenie: chasticy nachali obmenivat'sya okraskoj, stanovyas'
poperemenno to krasnymi, to belymi. Kazalos', budto krasnaya kraska
"pereprygivaet" s shara v pravoj ruke na shar v levoj ruke, a zatem s shara v
levoj ruke snova na shar v pravoj ruke. "Perekraska" sharov proishodila tak
bystro, chto kazalos', budto mezhdu sharami protyanulas' rozovataya lenta, po
kotoroj to v odnu, to v druguyu storonu peretekala kraska.
- Moi druz'ya-teoretiki nazyvayut eto obmennym vzaimodejstviem, - zametil
staryj master, posmeivayas' nad udivleniem mistera Tompkinsa. - Esli ugodno,
mozhno skazat', chto oba shara hotyat byt' krasnymi, no poskol'ku oni ne mogut
byt' krasnymi odnovremenno, shary kak by poperemenno peretyagivayut krasnuyu
okrasku k sebe. Ni odin iz sharov ne zhelaet ustupat' drugomu, i poetomu shary
vynuzhdeny prilipnut' drug k drugu i sosushchestvovat', pokuda vy ne razdelite
ih nasil'no. A teper' ya hochu pokazat' vam, kak prosto izgotovit' lyuboe yadro,
kakoe vy tol'ko pozhelaete. Kakoe yadro vam nravitsya bol'she drugih?
- Zoloto, - otvetil mister Tompkins, pomnya ob ambiciyah srednevekovyh
alhimikov.
- Zoloto? Sejchas posmotrim, - probormotal sebe pod nos staryj master,
oborachivayas' k ogromnoj tablice, visevshej na stene. - YAdro zolota vesit 197
edinic i neset 79 polozhitel'nyh elektricheskih zaryadov. Znachit, dlya
izgotovleniya yadra zolota ya dolzhen vzyat' 79 protonov i 118 nejtronov - togda
massa yadra poluchitsya pravil'noj.
Otschitav nuzhnoe kolichestvo sharov kazhdogo sorta, master pomestil ih v
vysokij cilindricheskij sosud i vstavil v nego tyazhelyj derevyannyj porshen'.
Zatem izo vseh sil on naleg na porshen', pytayas' sdvinut' ego vniz.
- |to neobhodimo dlya togo, - poyasnil on misteru Tompkinsu, - chtoby
preodolet' sil'noe elektricheskoe ottalkivanie mezhdu polozhitel'no zaryazhennymi
protonami. Lish' posle togo, kak szhatie porshnem preodoleet ottalkivanie
protonov, protony i nejtrony slipnutsya pod dejstviem obmennyh sil i obrazuyut
yadro zolota.
S siloj opustiv porshen' do otkaza vniz, master vynul ego i bystro
perevernul cilindricheskij sosud. Blestyashchij rozovatyj shar vykatilsya iz sosuda
na stol, i, prismotrevshis' povnimatel'nee, mister Tompkins ponyal, chto
rozovatyj cvet voznikal iz-za smesheniya krasnyh i belyh vspyshek, to i delo
proskakivavshih mezhdu bystro dvizhushchimisya chasticami.
- Kak krasivo! - voskliknul mister Tompkins. - Tak vot on kakoj, atom
zolota!
- Eshche ne atom, a tol'ko atomnoe yadro, - popravil ego staryj master. -
CHtoby zavershit' postroenie atoma, neobhodimo dobavit' nadlezhashchee kolichestvo
elektronov. Oni nejtralizuyut polozhitel'nyj zaryad yadra i sozdadut vokrug nego
obychnuyu elektronnuyu obolochku. Vprochem, sdelat' eto ne sostavlyaet osobogo
truda, tak kak yadro samo zahvatyvaet svoi elektrony, kak tol'ko te okazhutsya
poblizosti.
- Interesno, - zametil mister Tompkins. - Moj test' nikogda ne upominal
o tom, chto izgotovit' zoloto tak prosto.
- Vash test' i vse eti tak nazyvaemye fiziki-yadershchiki! - voskliknul
staryj master s notkami razdrazheniya v golose. - Ochen' uzh oni vazhnichayut, hotya
delat' umeyut ochen' malo. Oni utverzhdayut, budto protony nel'zya szhat' v
sostavnoe yadro, tak kak dlya etogo potrebovalos' by slishkom bol'shoe davlenie.
Odin iz nih dazhe podschital, chto dlya sblizheniya protonov ponadobilos' by
prilozhit' silu, ravnuyu vesu Luny. Tak pochemu by ne dostat' s neba Lunu, esli
im bol'she nechego delat'?
- No oni vse zhe nauchilis' osushchestvlyat' _nekotorye_ yadernye prevrashcheniya,
- myagko zametil mister Tompkins.
- Da, no s kakim trudom dayutsya im eti reakcii! A novye elementy oni
poluchayut v takih nichtozhnyh kolichestvah, chto sami zhe edva mogut ih
rassmotret'! YA sejchas prodemonstriruyu vam, kak oni eto delayut.
I shvativ proton, staryj master chto bylo sil zapustil im v yadro atoma
zolota, lezhavshee na stole. U samogo yadra proton chut' zamedlil svoe dvizhenie,
pokolebalsya kakoj-to moment i zatem nyrnul vnutr' yadra. Poglotiv proton,
yadro zatryaslos', slovno ot oznoba, a zatem ot nego s treskom otkololas'
nebol'shaya chast'.
- Vidite, - skazal master, podbiraya oskolok. - |to to, chto nazyvaetsya
al'fa-chasticej! Esli prismotret'sya povnimatel'nee, to vidno, chto ona sostoit
iz dvuh protonov i dvuh nejtronov. Takie chasticy obychno ispuskayutsya tyazhelymi
yadrami tak nazyvaemyh radioaktivnyh elementov, no al'fa-chasticu mozhno vybit'
i iz obychnyh stabil'nyh yader, esli stuknut' po nim dostatochno sil'no. Hochu
obratit' vashe vnimanie na to, chto ostavshijsya lezhat' na stole bolee krupnyj
oskolok uzhe ne yavlyaetsya yadrom atoma zolota. On utratil odin polozhitel'nyj
zaryad, i teper' pered nami yadro atoma platiny, predydushchego elementa v
periodicheskoj tablice. Odnako v nekotoryh sluchayah proton, proniknuv v yadro,
ne privodit k raspadu yadra na dva oskolka. V etom sluchae vy poluchite yadro
elementa, sleduyushchego za zolotom v periodicheskoj tablice, t. e. yadro rtuti.
Kombiniruya eti i analogichnye processy, mozhno prevrashchat' lyuboj element v
lyuboj drugoj.
- Teper' ya ponimayu, pochemu v yadernoj fizike ispol'zuyut puchki bystryh
protonov, razognannyh do vysokih energij na ciklotrone, - zadumchivo proiznes
mister Tompkins. - A pochemu vy schitaete, chto etot metod nehorosh?
- Potomu chto effektivnost' ego ochen' nizka. Prezhde vsego
fiziki-yadershchiki ne umeyut tak tochno popadat' v yadro, kak ya: u nih s yadrom
stalkivaetsya lish' odna chastica iz tysyachi. Vo-vtoryh, dazhe v tom sluchae, esli
chastica popala v yadro, ona s bol'shoj veroyatnost'yu ne pronikaet vnutr' yadra,
a otskakivaet ot nego. Vy, dolzhno byt', zametili, chto kogda ya zapustil
protonom v yadro atoma zolota, proton nemnogo pomedlil, prezhde chem vojti
vnutr' yadra i ya uzhe bylo podumal, chto proton otskochit nazad.
- A chto meshaet chasticam pronikat' v yadra? - pointeresovalsya mister
Tompkins.
- Ob etom vy mogli by dogadat'sya i sami, - skazal staryj master. - Esli
vy pomnite, i yadra, i bombardiruyushchie ih protony nesut polozhitel'nye zaryady.
Sily ottalkivaniya, dejstvuyushchie mezhdu etimi zaryadami, obrazuyut svoego roda
bar'er, preodolet' kotoryj ne tak-to legko. Esli bombardiruyushchie protony vse
zhe pronikayut v yadernuyu krepost', to proishodit eto tol'ko potomu, chto oni
ispol'zuyut priem, napominayushchij Troyanskogo konya: prohodyat skvoz' yadernye
steny, kak volny, a ne kak chasticy.
- Boyus', chto eto vyshe moego razumeniya, - pechal'no zametil mister
Tomgasins. - Iz vashih ob座asnenij ya ne ponyal ni slova.
- Boyus', chto eto tak, - skazal rezchik s ulybkoj. - Skazat' vam po
pravde, ya i sam ne ochen' razbirayus' vo vsem etom. Ved' ya master. YA mogu
delat' vse eti veshchi rukami, no v teoreticheskoj abrakadabre ya ne slishkom
silen. Glavnoe zdes' v tom, chto poskol'ku vse eti yadernye chasticy sdelany iz
kvantovogo materiala, oni legko prohodyat, ili prosachivayutsya, skvoz'
prepyatstviya, kotorye obychno schitayutsya nepronicaemymi.
- O, ya kazhetsya ponimayu, chto vy imeete v vidu! - voskliknul mister
Tompkins. - Pomnitsya, odnazhdy, eshche do togo, kak ya vstretil Mod, mne dovelos'
pobyvat' v odnom strannom meste, gde bil'yardnye shary veli sebya v tochnosti
tak, kak vy sejchas skazali. - Bil'yardnye shary? Vy imeete v vidu bil'yardnye
shary iz slonovoj kosti? - povtoril s gorech'yu staryj master.
- Da, naskol'ko ya znayu, shary byli vytocheny iz bivnej kvantovyh slonov,
- otvetil mister Tompkins.
- Nichego ne podelaesh', takova zhizn', - pechal'no skazal staryj master. -
Podumat' tol'ko, kto-to vyrezaet kakie-to durackie shary, rashoduya stol'
dragocennyj material dlya ch'ej-to zabavy, a mne prihoditsya vyrezat' protony i
nejtrony, fundamental'nejshie chasticy Vselennoj, iz prostogo kvantovogo duba!
- Vprochem, - prodolzhal on bodrym tonom, chtoby skryt' razocharovanie, -
moi neschastnye derevyannye igrushki nichut' ne ustupayut vsem etim dorogim
fintiflyushkam iz slonovoj kosti. Kak ya sejchas pokazhu vam, oni legko prohodyat
skvoz' lyuboj bar'er. Vzobravshis' na stul, master dostal s verhnej polki
reznuyu figurku neobychnogo vida, napominavshuyu model' vulkana.
- Vot, ne ugodno li vzglyanut', - prodolzhal master, ostorozhno smahivaya
pyl'. - Pered vami model' bar'era sil ottalkivaniya, kotoryj okruzhaet lyuboe
atomnoe yadro. Vneshnie sklony sootvetstvuyut ottalkivaniyu elektricheskih
zaryadov, a krater - silam scepleniya, uderzhivayushchim chasticy vnutri yadra. Esli
tolknut' sharik vverh po sklonu, no ne slishkom sil'no, chtoby on ne dostig
kraya kratera, to vy, estestvenno, ozhidaete, chto sharik skatitsya nazad. A vot
chto proishodit na samom dele.
- Da, da, - dobavil starichok, vidya izumlennoe vyrazhenie na lice mistera
Tompkinsa, - eta chastica cveta nefrita - ne chto inoe, kak obyknovennyj
elektron, nichem ne otlichayushchijsya ot drugih elektronov v lyubom atome i v chem
ugodno.
- Podumat' tol'ko! - voskliknul mister Tompkins. - |to dejstvitel'no
prevoshodit vse fokusy s raznocvetnymi nosovymi platkami, kakie tol'ko mne
prihodilos' videt'. A mozhete li vy vernut' sharam ih ishodnuyu okrasku?
- Da, ya votru zelenuyu krasku v poverhnost' krasnogo shara, ot chego shar
snova stanet belym. Razumeetsya, dlya etogo pridetsya zatratit' opredelennoe
kolichestvo energii. Drugoj sposob sostoit v tom, chtoby soskresti s shara
krasnuyu krasku, no i on trebuet zatrat energii. Soskoblennaya s poverhnosti
protona krasnaya kraska obrazuet krasnuyu kaplyu, t. e. polozhitel'no zaryazhennyj
elektron, o kotorom vam, dolzhno byt', prihodilos' slyshat'.
- O da, kogda ya byl elektronom, - nachal bylo mister Tompkins, no vo
vremya spohvatilsya, - t. e. ya hochu skazat', chto slyshal, budto polozhitel'nye i
otricatel'nye elektrony pri stolknovenii annigiliruyut, t. e. vzaimno
unichtozhayutsya. Ne mogli by vy prodelat' etot tryuk dlya menya?
- S udovol'stviem, - otvetil staryj master. - Delaetsya eto ochen'
prosto. YA ne stanu soskrebat' krasku s etogo protona. U menya i tak ostalas'
parochka-drugaya protonov ot utrennej raboty.
Otkryv odin iz yashchikov, on izvlek iz nego nebol'shoj yarko-krasnyj shar i,
krepko derzha ego mezhdu ukazatel'nym i bol'shim pal'cami, prizhal k zelenomu
sharu, lezhavshemu na stole. Posledoval gromkij tresk, slovno vzorvalas'
hlopushka, i oba shara odnovremenno ischezli.
- Videli? - sprosil rezchik, duya na slegka obozhzhennye pal'cy. - Poetomu
iz elektronov i nel'zya stroit' yadra. Odnazhdy ya popytalsya, no potom brosil
etu zateyu i teper' stroyu yadra tol'ko iz protonov i nejtronov.
- No ved' nejtrony tozhe nestabil'ny, esli ya ne oshibayus'? - sprosil
mister Tompkins, vspominaya prevrashcheniya belogo shara.
- Esli brat' nejtrony poodinochke, to oni dejstvitel'no nestabil'ny. No
kogda oni plotno upakovany v yadre i okruzheny drugimi chasticami, to
stanovyatsya stabil'nymi. Esli zhe nejtronov ili protonov stanovitsya slishkom
mnogo, to oni mogut preterpevat' prevrashcheniya i ispuskat' iz yadra lishnyuyu
krasku v vide polozhitel'no ili otricatel'no zaryazhennyh elektronov. Takie
sobytiya my nazyvaem beta-raspadom.
- Ispol'zuete li vy pri izgotovlenii yader klej? - pointeresovalsya
mister Tompkins.
- Net, nikakoj klej mne ne nuzhen, - otvetil staryj master. - |ti
chasticy, izvol'te videt', sami slipayutsya, stoit lish' podnesti ih drug k
drugu. Poprobujte sami, esli hotite.
Posledovav etomu lyubeznomu priglasheniyu, mister Tompkins vzyal v odnu
ruku proton, v druguyu nejtron i ostorozhno nachal ih sblizhat'. On srazu zhe
pochuvstvoval sil'noe prityazhenie i, vzglyanuv na chasticy, zametil chrezvychajno
strannoe yavlenie: chasticy nachali obmenivat'sya okraskoj, stanovyas'
poperemenno to krasnymi, to belymi. Kazalos', budto krasnaya kraska
"pereprygivaet" s shara v pravoj ruke na shar v levoj ruke, a zatem s shara v
levoj ruke snova na shar v pravoj ruke. "Perekraska" sharov proishodila tak
bystro, chto kazalos', budto mezhdu sharami protyanulas' rozovataya lenta, po
kotoroj to v odnu, to v druguyu storonu peretekala kraska.
- Moi druz'ya-teoretiki nazyvayut eto obmennym vzaimodejstviem, - zametil
staryj master, posmeivayas' nad udivleniem mistera Tompkinsa. - Esli ugodno,
mozhno skazat', chto oba shara hotyat byt' krasnymi, no poskol'ku oni ne mogut
byt' krasnymi odnovremenno, shary kak by poperemenno peretyagivayut krasnuyu
okrasku k sebe. Ni odin iz sharov ne zhelaet ustupat' drugomu, i poetomu shary
vynuzhdeny prilipnut' drug k drugu i sosushchestvovat', pokuda vy ne razdelite
ih nasil'no. A teper' ya hochu pokazat' vam, kak prosto izgotovit' lyuboe yadro,
kakoe vy tol'ko pozhelaete. Kakoe yadro vam nravitsya bol'she drugih?
- Zoloto, - otvetil mister Tompkins, pomnya ob ambiciyah srednevekovyh
alhimikov.
- Zoloto? Sejchas posmotrim, - probormotal sebe pod nos staryj master,
oborachivayas' k ogromnoj tablice, visevshej na stene. - YAdro zolota vesit 197
edinic i neset 79 polozhitel'nyh elektricheskih zaryadov. Znachit, dlya
izgotovleniya yadra zolota ya dolzhen vzyat' 79 protonov i 118 nejtronov - togda
massa yadra poluchitsya pravil'noj.
Otschitav nuzhnoe kolichestvo sharov kazhdogo sorta, master pomestil ih v
vysokij cilindricheskij sosud i vstavil v nego tyazhelyj derevyannyj porshen'.
Zatem izo vseh sil on naleg na porshen', pytayas' sdvinut' ego vniz.
- |to neobhodimo dlya togo, - poyasnil on misteru Tompkinsu, - chtoby
preodolet' sil'noe elektricheskoe ottalkivanie mezhdu polozhitel'no zaryazhennymi
protonami. Lish' posle togo, kak szhatie porshnem preodoleet ottalkivanie
protonov, protony i nejtrony slipnutsya pod dejstviem obmennyh sil i obrazuyut
yadro zolota.
S siloj opustiv porshen' do otkaza vniz, master vynul ego i bystro
perevernul cilindricheskij sosud. Blestyashchij rozovatyj shar vykatilsya iz sosuda
na stol, i, prismotrevshis' povnimatel'nee, mister Tompkins ponyal, chto
rozovatyj cvet voznikal iz-za smesheniya krasnyh i belyh vspyshek, to i delo
proskakivavshih mezhdu bystro dvizhushchimisya chasticami.
- Kak krasivo! - voskliknul mister Tompkins. - Tak vot on kakoj, atom
zolota!
- Eshche ne atom, a tol'ko atomnoe yadro, - popravil ego staryj master. -
CHtoby zavershit' postroenie atoma, neobhodimo dobavit' nadlezhashchee kolichestvo
elektronov. Oni nejtralizuyut polozhitel'nyj zaryad yadra i sozdadut vokrug nego
obychnuyu elektronnuyu obolochku. Vprochem, sdelat' eto ne sostavlyaet osobogo
truda, tak kak yadro samo zahvatyvaet svoi elektrony, kak tol'ko te okazhutsya
poblizosti.
- Interesno, - zametil mister Tompkins. - Moj test' nikogda ne upominal
o tom, chto izgotovit' zoloto tak prosto.
- Vash test' i vse eti tak nazyvaemye fiziki-yadershchiki! - voskliknul
staryj master s notkami razdrazheniya v golose. - Ochen' uzh oni vazhnichayut, hotya
delat' umeyut ochen' malo. Oni utverzhdayut, budto protony nel'zya szhat' v
sostavnoe yadro, tak kak dlya etogo potrebovalos' by slishkom bol'shoe davlenie.
Odin iz nih dazhe podschital, chto dlya sblizheniya protonov ponadobilos' by
prilozhit' silu, ravnuyu vesu Luny. Tak pochemu by ne dostat' s neba Lunu, esli
im bol'she nechego delat'?
- No oni vse zhe nauchilis' osushchestvlyat' _nekotorye_ yadernye prevrashcheniya,
- myagko zametil mister Tompkins.
- Da, no s kakim trudom dayutsya im eti reakcii! A novye elementy oni
poluchayut v takih nichtozhnyh kolichestvah, chto sami zhe edva mogut ih
rassmotret'! YA sejchas prodemonstriruyu vam, kak oni eto delayut.
I shvativ proton, staryj master chto bylo sil zapustil im v yadro atoma
zolota, lezhavshee na stole. U samogo yadra proton chut' zamedlil svoe dvizhenie,
pokolebalsya kakoj-to moment i zatem nyrnul vnutr' yadra. Poglotiv proton,
yadro zatryaslos', slovno ot oznoba, a zatem ot nego s treskom otkololas'
nebol'shaya chast'.
- Vidite, - skazal master, podbiraya oskolok. - |to to, chto nazyvaetsya
al'fa-chasticej! Esli prismotret'sya povnimatel'nee, to vidno, chto ona sostoit
iz dvuh protonov i dvuh nejtronov. Takie chasticy obychno ispuskayutsya tyazhelymi
yadrami tak nazyvaemyh radioaktivnyh elementov, no al'fa-chasticu mozhno vybit'
i iz obychnyh stabil'nyh yader, esli stuknut' po nim dostatochno sil'no. Hochu
obratit' vashe vnimanie na to, chto ostavshijsya lezhat' na stole bolee krupnyj
oskolok uzhe ne yavlyaetsya yadrom atoma zolota. On utratil odin polozhitel'nyj
zaryad, i teper' pered nami yadro atoma platiny, predydushchego elementa v
periodicheskoj tablice. Odnako v nekotoryh sluchayah proton, proniknuv v yadro,
ne privodit k raspadu yadra na dva oskolka. V etom sluchae vy poluchite yadro
elementa, sleduyushchego za zolotom v periodicheskoj tablice, t. e. yadro rtuti.
Kombiniruya eti i analogichnye processy, mozhno prevrashchat' lyuboj element v
lyuboj drugoj.
- Teper' ya ponimayu, pochemu v yadernoj fizike ispol'zuyut puchki bystryh
protonov, razognannyh do vysokih energij na ciklotrone, - zadumchivo proiznes
mister Tompkins. - A pochemu vy schitaete, chto etot metod nehorosh?
- Potomu chto effektivnost' ego ochen' nizka. Prezhde vsego
fiziki-yadershchiki ne umeyut tak tochno popadat' v yadro, kak ya: u nih s yadrom
stalkivaetsya lish' odna chastica iz tysyachi. Vo-vtoryh, dazhe v tom sluchae, esli
chastica popala v yadro, ona s bol'shoj veroyatnost'yu ne pronikaet vnutr' yadra,
a otskakivaet ot nego. Vy, dolzhno byt', zametili, chto kogda ya zapustil
protonom v yadro atoma zolota, proton nemnogo pomedlil, prezhde chem vojti
vnutr' yadra i ya uzhe bylo podumal, chto proton otskochit nazad.
- A chto meshaet chasticam pronikat' v yadra? - pointeresovalsya mister
Tompkins.
- Ob etom vy mogli by dogadat'sya i sami, - skazal staryj master. - Esli
vy pomnite, i yadra, i bombardiruyushchie ih protony nesut polozhitel'nye zaryady.
Sily ottalkivaniya, dejstvuyushchie mezhdu etimi zaryadami, obrazuyut svoego roda
bar'er, preodolet' kotoryj ne tak-to legko. Esli bombardiruyushchie protony vse
zhe pronikayut v yadernuyu krepost', to proishodit eto tol'ko potomu, chto oni
ispol'zuyut priem, napominayushchij Troyanskogo konya: prohodyat skvoz' yadernye
steny, kak volny, a ne kak chasticy.
- Boyus', chto eto vyshe moego razumeniya, - pechal'no zametil mister
Tomgasins. - Iz vashih ob座asnenij ya ne ponyal ni slova.
- Boyus', chto eto tak, - skazal rezchik s ulybkoj. - Skazat' vam po
pravde, ya i sam ne ochen' razbirayus' vo vsem etom. Ved' ya master. YA mogu
delat' vse eti veshchi rukami, no v teoreticheskoj abrakadabre ya ne slishkom
silen. Glavnoe zdes' v tom, chto poskol'ku vse eti yadernye chasticy sdelany iz
kvantovogo materiala, oni legko prohodyat, ili prosachivayutsya, skvoz'
prepyatstviya, kotorye obychno schitayutsya nepronicaemymi.
- O, ya kazhetsya ponimayu, chto vy imeete v vidu! - voskliknul mister
Tompkins. - Pomnitsya, odnazhdy, eshche do togo, kak ya vstretil Mod, mne dovelos'
pobyvat' v odnom strannom meste, gde bil'yardnye shary veli sebya v tochnosti
tak, kak vy sejchas skazali. - Bil'yardnye shary? Vy imeete v vidu bil'yardnye
shary iz slonovoj kosti? - povtoril s gorech'yu staryj master.
- Da, naskol'ko ya znayu, shary byli vytocheny iz bivnej kvantovyh slonov,
- otvetil mister Tompkins.
- Nichego ne podelaesh', takova zhizn', - pechal'no skazal staryj master. -
Podumat' tol'ko, kto-to vyrezaet kakie-to durackie shary, rashoduya stol'
dragocennyj material dlya ch'ej-to zabavy, a mne prihoditsya vyrezat' protony i
nejtrony, fundamental'nejshie chasticy Vselennoj, iz prostogo kvantovogo duba!
- Vprochem, - prodolzhal on bodrym tonom, chtoby skryt' razocharovanie, -
moi neschastnye derevyannye igrushki nichut' ne ustupayut vsem etim dorogim
fintiflyushkam iz slonovoj kosti. Kak ya sejchas pokazhu vam, oni legko prohodyat
skvoz' lyuboj bar'er. Vzobravshis' na stul, master dostal s verhnej polki
reznuyu figurku neobychnogo vida, napominavshuyu model' vulkana.
- Vot, ne ugodno li vzglyanut', - prodolzhal master, ostorozhno smahivaya
pyl'. - Pered vami model' bar'era sil ottalkivaniya, kotoryj okruzhaet lyuboe
atomnoe yadro. Vneshnie sklony sootvetstvuyut ottalkivaniyu elektricheskih
zaryadov, a krater - silam scepleniya, uderzhivayushchim chasticy vnutri yadra. Esli
tolknut' sharik vverh po sklonu, no ne slishkom sil'no, chtoby on ne dostig
kraya kratera, to vy, estestvenno, ozhidaete, chto sharik skatitsya nazad. A vot
chto proishodit na samom dele.
 Master slegka podtolknul sharik vverh po sklonu.
- Ne vizhu nichego neobychnogo, - zametil mister Tompkins, kogda sharik,
podnyavshis' primerno do serediny sklona, skatilsya nazad.
- Ne toropites', - spokojno skazal master. - Ne vse i ne vsegda
poluchaetsya s pervogo raza.
On eshche raz tolknul sharik vverh po sklonu, i sharik snova skatilsya vniz.
I lish' s tret'ej popytki sharik, podnyavshis' primerno do serediny sklona,
vnezapno ischez.
- Kak vy dumaete, gde teper' sharik? - torzhestvuyushche sprosil staryj
master s chuvstvom fokusnika, udachno vypolnivshego trudnyj tryuk.
- Navernoe, v kratere? - vyskazal predpolozhenie mister Tompkins.
- Vy sovershenno pravy, imenno v kratere, - podtverdil ego dogadku
staryj master, vynimaya sharik iz uglubleniya dvumya pal'cami.
- A teper' poprobuem zapustit' ego v obratnom napravlenii, - predlozhil
on misteru Tompkinsu, - i posmotrim, smozhet li sharik vybrat'sya iz kratera,
ne perekatyvayas' cherez kraj.
V techenie kakogo-to vremeni nichego ne proishodilo, i mister Tompkins
mog tol'ko slyshat' pogromyhivanie sharika, katavshegosya to v odnu, to v druguyu
storonu vnutri kratera. Zatem, kak po manoveniyu volshebnoj palochki, sharik
vdrug poyavilsya na seredine sklona i tiho skatilsya na stol.
- To, chto vy sejchas videli, mozhet sluzhit' horoshej illyustraciej togo,
chto proishodit pri radioaktivnom al'fa-raspade, - skazal rezchik, stavya
model' na polku, - tol'ko tam vmesto bar'era iz obychnogo kvantovogo duba
sushchestvuet bar'er sil ottalkivaniya elektricheskih zaryadov. V principe nikakoj
raznicy mezhdu model'yu i nastoyashchim al'fa-raspadom net. Inogda eti
elektricheskie bar'ery v atomah stanovyatsya nastol'ko "prozrachnymi", chto
chasticy pokidayut yadra za nichtozhnuyu dolyu sekundy. V drugih sluchayah yadernye
bar'ery nastol'ko "neprozrachnye", chto perehod iz yadra naruzhu zatyagivaetsya na
mnogie milliardy let, kak naprimer v yadre urana.
- No pochemu ne vse yadra radioaktivny? - pointeresovalsya mister
Tomtpsins.
- Potomu chto u bol'shinstva yader dno kratera raspolozheno nizhe urovnya
podoshvy vulkana, i tol'ko u samyh tyazhelyh iz izvestnyh yader dno kratera
podnyato dostatochno vysoko dlya togo, chtoby "pobeg" chasticy mog sostoyat'sya.
Trudno skazat', skol'ko chasov provel mister Tomtpsins v masterskoj u
milogo starogo mastera, s gotovnost'yu delivshegosya s nim svoimi poznaniyami na
lyubuyu temu, kotoruyu oni zatragivali v besede. Master pokazal misteru
Tompkinsu mnozhestvo neobychnyh veshchej, v tom chisle tshchatel'no zakrytuyu, no,
po-vidimomu, pustuyu shkatulku s nadpis'yu "NEJTRINO. _Obrashchat'sya s
ostorozhnost'yu_".
- Tam vnutri chto-nibud' est'? - s lyubopytstvom sprosil mister Tompkins,
vstryahivaya shkatulku u samogo uha.
- Ne znayu, - priznalsya staryj master. - Odni govoryat, chto est', drugie,
chto net. No vnutri shkatulki vy vse ravno nichego ne uvidite. |tu zanyatnuyu
shkatulku podaril mne odin priyatel', fizik-teoretik, i, po pravde govorya, ya
ne znayu, chto s nej delat'. Luchshe vsego poka ostavit' ee v pokoe.
Prodolzhaya osmatrivat' masterskuyu, mister Tompkins uvidel na verstake
pokrytuyu pyl'yu starinnuyu skripku. Ona kazalas' takoj staroj, slovno ee
izgotovil dedushka Stradivari.
- Vy igraete na skripke? - povernulsya k rezchiku mister Tompkins.
- Tol'ko gamma-melodii, - otvetil staryj master. - |to kvantovaya
skripka, i nichego drugogo na nej ispolnit' nel'zya. Kogda-to u menya byla
kvantovaya violonchel'. Na nej mozhno bylo ispolnyat' melodii v opticheskom
diapazone, no kto-to poprosil ee u menya poigrat', da tak i ne udosuzhilsya
vernut'.
Master slegka podtolknul sharik vverh po sklonu.
- Ne vizhu nichego neobychnogo, - zametil mister Tompkins, kogda sharik,
podnyavshis' primerno do serediny sklona, skatilsya nazad.
- Ne toropites', - spokojno skazal master. - Ne vse i ne vsegda
poluchaetsya s pervogo raza.
On eshche raz tolknul sharik vverh po sklonu, i sharik snova skatilsya vniz.
I lish' s tret'ej popytki sharik, podnyavshis' primerno do serediny sklona,
vnezapno ischez.
- Kak vy dumaete, gde teper' sharik? - torzhestvuyushche sprosil staryj
master s chuvstvom fokusnika, udachno vypolnivshego trudnyj tryuk.
- Navernoe, v kratere? - vyskazal predpolozhenie mister Tompkins.
- Vy sovershenno pravy, imenno v kratere, - podtverdil ego dogadku
staryj master, vynimaya sharik iz uglubleniya dvumya pal'cami.
- A teper' poprobuem zapustit' ego v obratnom napravlenii, - predlozhil
on misteru Tompkinsu, - i posmotrim, smozhet li sharik vybrat'sya iz kratera,
ne perekatyvayas' cherez kraj.
V techenie kakogo-to vremeni nichego ne proishodilo, i mister Tompkins
mog tol'ko slyshat' pogromyhivanie sharika, katavshegosya to v odnu, to v druguyu
storonu vnutri kratera. Zatem, kak po manoveniyu volshebnoj palochki, sharik
vdrug poyavilsya na seredine sklona i tiho skatilsya na stol.
- To, chto vy sejchas videli, mozhet sluzhit' horoshej illyustraciej togo,
chto proishodit pri radioaktivnom al'fa-raspade, - skazal rezchik, stavya
model' na polku, - tol'ko tam vmesto bar'era iz obychnogo kvantovogo duba
sushchestvuet bar'er sil ottalkivaniya elektricheskih zaryadov. V principe nikakoj
raznicy mezhdu model'yu i nastoyashchim al'fa-raspadom net. Inogda eti
elektricheskie bar'ery v atomah stanovyatsya nastol'ko "prozrachnymi", chto
chasticy pokidayut yadra za nichtozhnuyu dolyu sekundy. V drugih sluchayah yadernye
bar'ery nastol'ko "neprozrachnye", chto perehod iz yadra naruzhu zatyagivaetsya na
mnogie milliardy let, kak naprimer v yadre urana.
- No pochemu ne vse yadra radioaktivny? - pointeresovalsya mister
Tomtpsins.
- Potomu chto u bol'shinstva yader dno kratera raspolozheno nizhe urovnya
podoshvy vulkana, i tol'ko u samyh tyazhelyh iz izvestnyh yader dno kratera
podnyato dostatochno vysoko dlya togo, chtoby "pobeg" chasticy mog sostoyat'sya.
Trudno skazat', skol'ko chasov provel mister Tomtpsins v masterskoj u
milogo starogo mastera, s gotovnost'yu delivshegosya s nim svoimi poznaniyami na
lyubuyu temu, kotoruyu oni zatragivali v besede. Master pokazal misteru
Tompkinsu mnozhestvo neobychnyh veshchej, v tom chisle tshchatel'no zakrytuyu, no,
po-vidimomu, pustuyu shkatulku s nadpis'yu "NEJTRINO. _Obrashchat'sya s
ostorozhnost'yu_".
- Tam vnutri chto-nibud' est'? - s lyubopytstvom sprosil mister Tompkins,
vstryahivaya shkatulku u samogo uha.
- Ne znayu, - priznalsya staryj master. - Odni govoryat, chto est', drugie,
chto net. No vnutri shkatulki vy vse ravno nichego ne uvidite. |tu zanyatnuyu
shkatulku podaril mne odin priyatel', fizik-teoretik, i, po pravde govorya, ya
ne znayu, chto s nej delat'. Luchshe vsego poka ostavit' ee v pokoe.
Prodolzhaya osmatrivat' masterskuyu, mister Tompkins uvidel na verstake
pokrytuyu pyl'yu starinnuyu skripku. Ona kazalas' takoj staroj, slovno ee
izgotovil dedushka Stradivari.
- Vy igraete na skripke? - povernulsya k rezchiku mister Tompkins.
- Tol'ko gamma-melodii, - otvetil staryj master. - |to kvantovaya
skripka, i nichego drugogo na nej ispolnit' nel'zya. Kogda-to u menya byla
kvantovaya violonchel'. Na nej mozhno bylo ispolnyat' melodii v opticheskom
diapazone, no kto-to poprosil ee u menya poigrat', da tak i ne udosuzhilsya
vernut'.
 - Sygrajte mne, pozhalujsta, kakuyu-nibud' gamma-melodiyu, - poprosil
mister Tompkins. - Mne ne prihodilos' slyshat' takie melodii prezhde.
- YA sygrayu vam "Nukleat v tonal'nosti Th S diez", - skazal staryj
master, berya skripku, - no prigotov'tes', eto ochen' pechal'naya melodiya.
Muzyka, dejstvitel'no, zvuchala ochen' stranno. Nichego pohozhego misteru
Tompkinsu slyshat' ne prihodilos'. Melodiya napominala neumolchnyj shum morskih
voln, nakatyvayushchihsya na peschanyj bereg. Vremya ot vremeni shum priboya preryval
rezkij zvuk, napominavshij svist proletevshej mimo puli. Mister Tompkins ne
byl zavzyatym melomanom, no ispolnyaemaya masterom melodiya zacharovala i skovala
ego. On potyanulsya, ustroilsya poudobnee v starom kresle i zakryl glaza...
Glava 14
Dyry v pustote
Ledi i dzhentl'meny!
Segodnya ya proshu vas byt' osobenno vnimatel'nymi, poskol'ku problemy, o
kotoryh pojdet rech' v moej lekcii, stol' zhe trudny, skol' i uvlekatel'ny. YA
namerevayus' rasskazat' vam o novyh chasticah, izvestnyh pod nazvaniem
pozitrony i obladayushchih bolee chem neobychnymi svojstvami. Ves'ma pouchitel'no,
chto sushchestvovanie etoj novoj raznovidnosti chastic bylo predskazano na osnove
chisto teoreticheskih soobrazhenij za neskol'ko let do togo, kak oni byli
obnaruzheny eksperimental'no, otkrytiyu pozitronov v znachitel'noj mere
sposobstvovalo teoreticheskoe predskazanie ih osnovnyh svojstv.
CHest' sdelat' eti predskazaniya prinadlezhit britanskomu fiziku Polyu
Diraku, o kotorom vam uzhe prihodilos' slyshat'. K svoim zaklyucheniyam Dirak
prishel na osnove teoreticheskih soobrazhenij, stol' neobychnyh i
fantasticheskih, chto bol'shinstvo fizikov dolgoe vremya otkazyvalos' verit' v
nih. Osnovnuyu ideyu teorii Diraka mozhno sformulirovat' v sleduyushchih prostyh
slovah: "V pustom prostranstve dolzhny byt' dyry". YA vizhu, vy udivleny. Ne
menee vas byli udivleny i fiziki, kogda Dirak vpervye proiznes eti slova.
Kak mogut byt' dyry v pustom prostranstve? Est' li v podobnom utverzhdenii
kakoj-nibud' smysl? Okazyvaetsya, est', esli vspomnit', chto tak nazyvaemoe
pustoe prostranstvo v dejstvitel'nosti ne tak pusto, kak nam kazhetsya. V
samom dele, osnovnym ishodnym punktom teorii Diraka sluzhit predpolozhenie o
tom, chto _tak nazyvaemoe pustoe prostranstvo, ili vakuum, v dejstvitel'nosti
plotno zapolneno beskonechno mnogimi elektronami (obychnymi otricatel'no
zaryazhennymi elektronami), upakovannymi ves'ma pravil'no i ravnomerno_. Net
neobhodimosti govorit' o tom, chto eta staraya gipoteza prishla Diraku v golovu
ne prosto kak igra fantazii. K prinyatiyu ee Diraka vynudil celyj ryad
soobrazhenij, svyazannyh s teoriej obychnyh otricatel'no zaryazhennyh elektronov.
|ta teoriya privodit k neizbezhnomu zaklyucheniyu o tom, chto pomimo kvantovyh
sostoyanij dvizheniya v atome sushchestvuet takzhe beskonechno mnogo osobyh
_otricatel'nyh kvantovyh sostoyanij_, prinadlezhashchih chistomu vakuumu i chto
elektrony, esli nichto ne meshaet im perehodit' v eti "bolee udobnye"
sostoyaniya dvizheniya, pokinut svoi atomy i, tak skazat', rastvoryatsya v pustom
prostranstve. Bolee togo, poskol'ku sushchestvuet tol'ko odin sposob
vosprepyatstvovat' elektronu perehodit', kuda emu zablagorassuditsya, a imenno
zanyat' to sostoyanie, v kotoroe sobiraetsya perehodit' elektron, drugim
elektronom (vspomnite princip Pauli!), vse sostoyaniya v vakuume dolzhny byt'
zapolneny beskonechno mnogimi elektronami, ravnomerno raspredelennymi po
vsemu prostranstvu.
Boyus', chto moi slova zvuchat dlya vas, kak svoego roda nauchnaya
abrakadabra i chto golova u vas ot vsego etogo vdet krugom. Dolzhen zametit',
chto predmet moej lekcii segodnya osobenno truden, no ya nadeyus', chto esli vy
budete vnimatel'no slushat' menya, to v konce koncov vam udastsya sostavit'
opredelennoe predstavlenie o haraktere teorii Diraka.
No vernemsya k teme lekcii. Tak ili inache Dirak prishel k zaklyucheniyu o
tom, chto pustoe prostranstvo do otkaza zapolneno elektronami,
raspredelennymi ravnomerno, no s beskonechno bol'shoj plotnost'yu. Kak moglo
sluchit'sya, chto my voobshche ne zamechaem stol' gustogo skopleniya elektronov i
rassmatrivaem vakuum kak absolyutnoe prostranstvo?
Vy smozhete luchshe ponyat' otvet na eti voprosy, esli voobrazite sebya
glubokovodnoj ryboj, nahodyashchejsya v tolshche vod. Ponimaet li ryba, razumeetsya,
esli ona nadelena dostatochno razvitym intellektom dlya togo, chtoby zadat'
sebe vopros, chto ona okruzhena vodoj?
|ti slova vyveli mistera Tompkinsa iz dremoty, v kotoruyu on pogruzilsya
v nachale lekcii. On byl zayadlym rybakom i dazhe pochuvstvoval na svoem lice
svezhee dyhanie morskogo vetra i voochiyu uvidel plavno katyashchiesya volny. No
hotya mister Tompkins neploho plaval, pochemu-to na etot raz emu bylo trudno
uderzhat'sya na poverhnosti i on nachal medlenno idti ko dnu, opuskayas' vse
glubzhe i glubzhe. Kak ni stranno, no on ne oshchushchal nehvatki vozduha i
chuvstvoval sebya vpolne komfortno.
- Mozhet byt', - podumal on, - so mnoj proizoshla kakaya-nibud' osobaya
recessivnaya mutaciya?
Po dannym paleontologov, zhizn' zarodilas' v okeane i pervymi, kto
vybralsya iz vody na sushu, byli tak nazyvaemye _dvoyakodyshashchie_ ryby, hodivshie
na plavnikah. Po mneniyu biologov, eti pervye dvoyakodyshashchie ryby, kotoryh
nazyvayut po-raznomu (v Avstralii rogozubami, v Afrike protopterami, v YUzhnoj
Amerike cheshujchatnikami ili lepidosirenami), postepenno prevratilis' v
suhoputnyh zhivotnyh, takih kak myshi i koshki, i v lyudej. Nekotorye iz
zhivotnyh, naprimer, kity i del'finy, oznakomivshis' so vsemi trudnostyami
zhizni na sushe, vernulis' v okean. No i posle vozvrashcheniya v vodu oni
sohranili kachestva, priobretennye vo vremya bor'by za sushchestvovanie na sushe,
naprimer, ostalis' mlekopitayushchimi, ih samki vynashivayut potomstvo vnutri
svoego tela, a ne otkladyvayut ikru, kotoruyu zatem oplodotvoryayut samcy. Razve
znamenityj vengerskij uchenyj Leo Scilard {Avtor imeet v vidu
nauchno-fantasticheskuyu novellu Leo Scilarda "Golos del'finov".} ne skazal
kak-to, chto del'finy obladayut bolee razvitym intellektom, chem lyudi?
Tut razmyshleniya mistera Tompkinsa byli prervany razgovorom,
proishodivshim gde-to gluboko pod poverhnost'yu okeana mezhdu del'finom i
tipichnym gomo sapiensom, v kotorom Tompkins (po nekogda vidennoj fotografii)
srazu uznal fizika iz Kembridzhskogo universiteta Polya Adriena Morisa Diraka.
- Poslushaj, Pol', - govoril del'fin, - ty schitaesh', chto my nahodimsya ne
v vakuume, a v material'noj srede, sostoyashchej iz chastic s otricatel'noj
massoj. YA lichno schitayu, chto voda nichem ne otlichaetsya ot pustogo
prostranstva. Ona sovershenno odnorodna, i smogu svobodno dvigat'sya v nej po
vsem napravleniyam. Odnako ot svoego dalekogo predka -
pra-pra-pra-pra-pradedushki - ya slyshal legendu o tom, chto na sushe vse inache.
Tam est' gory i ushchel'ya, preodolet' kotorye stoit nemalyh usilij. Zdes', v
vode, ya mogu dvigat'sya v lyubuyu storonu, kuda zahochu.
- Sygrajte mne, pozhalujsta, kakuyu-nibud' gamma-melodiyu, - poprosil
mister Tompkins. - Mne ne prihodilos' slyshat' takie melodii prezhde.
- YA sygrayu vam "Nukleat v tonal'nosti Th S diez", - skazal staryj
master, berya skripku, - no prigotov'tes', eto ochen' pechal'naya melodiya.
Muzyka, dejstvitel'no, zvuchala ochen' stranno. Nichego pohozhego misteru
Tompkinsu slyshat' ne prihodilos'. Melodiya napominala neumolchnyj shum morskih
voln, nakatyvayushchihsya na peschanyj bereg. Vremya ot vremeni shum priboya preryval
rezkij zvuk, napominavshij svist proletevshej mimo puli. Mister Tompkins ne
byl zavzyatym melomanom, no ispolnyaemaya masterom melodiya zacharovala i skovala
ego. On potyanulsya, ustroilsya poudobnee v starom kresle i zakryl glaza...
Glava 14
Dyry v pustote
Ledi i dzhentl'meny!
Segodnya ya proshu vas byt' osobenno vnimatel'nymi, poskol'ku problemy, o
kotoryh pojdet rech' v moej lekcii, stol' zhe trudny, skol' i uvlekatel'ny. YA
namerevayus' rasskazat' vam o novyh chasticah, izvestnyh pod nazvaniem
pozitrony i obladayushchih bolee chem neobychnymi svojstvami. Ves'ma pouchitel'no,
chto sushchestvovanie etoj novoj raznovidnosti chastic bylo predskazano na osnove
chisto teoreticheskih soobrazhenij za neskol'ko let do togo, kak oni byli
obnaruzheny eksperimental'no, otkrytiyu pozitronov v znachitel'noj mere
sposobstvovalo teoreticheskoe predskazanie ih osnovnyh svojstv.
CHest' sdelat' eti predskazaniya prinadlezhit britanskomu fiziku Polyu
Diraku, o kotorom vam uzhe prihodilos' slyshat'. K svoim zaklyucheniyam Dirak
prishel na osnove teoreticheskih soobrazhenij, stol' neobychnyh i
fantasticheskih, chto bol'shinstvo fizikov dolgoe vremya otkazyvalos' verit' v
nih. Osnovnuyu ideyu teorii Diraka mozhno sformulirovat' v sleduyushchih prostyh
slovah: "V pustom prostranstve dolzhny byt' dyry". YA vizhu, vy udivleny. Ne
menee vas byli udivleny i fiziki, kogda Dirak vpervye proiznes eti slova.
Kak mogut byt' dyry v pustom prostranstve? Est' li v podobnom utverzhdenii
kakoj-nibud' smysl? Okazyvaetsya, est', esli vspomnit', chto tak nazyvaemoe
pustoe prostranstvo v dejstvitel'nosti ne tak pusto, kak nam kazhetsya. V
samom dele, osnovnym ishodnym punktom teorii Diraka sluzhit predpolozhenie o
tom, chto _tak nazyvaemoe pustoe prostranstvo, ili vakuum, v dejstvitel'nosti
plotno zapolneno beskonechno mnogimi elektronami (obychnymi otricatel'no
zaryazhennymi elektronami), upakovannymi ves'ma pravil'no i ravnomerno_. Net
neobhodimosti govorit' o tom, chto eta staraya gipoteza prishla Diraku v golovu
ne prosto kak igra fantazii. K prinyatiyu ee Diraka vynudil celyj ryad
soobrazhenij, svyazannyh s teoriej obychnyh otricatel'no zaryazhennyh elektronov.
|ta teoriya privodit k neizbezhnomu zaklyucheniyu o tom, chto pomimo kvantovyh
sostoyanij dvizheniya v atome sushchestvuet takzhe beskonechno mnogo osobyh
_otricatel'nyh kvantovyh sostoyanij_, prinadlezhashchih chistomu vakuumu i chto
elektrony, esli nichto ne meshaet im perehodit' v eti "bolee udobnye"
sostoyaniya dvizheniya, pokinut svoi atomy i, tak skazat', rastvoryatsya v pustom
prostranstve. Bolee togo, poskol'ku sushchestvuet tol'ko odin sposob
vosprepyatstvovat' elektronu perehodit', kuda emu zablagorassuditsya, a imenno
zanyat' to sostoyanie, v kotoroe sobiraetsya perehodit' elektron, drugim
elektronom (vspomnite princip Pauli!), vse sostoyaniya v vakuume dolzhny byt'
zapolneny beskonechno mnogimi elektronami, ravnomerno raspredelennymi po
vsemu prostranstvu.
Boyus', chto moi slova zvuchat dlya vas, kak svoego roda nauchnaya
abrakadabra i chto golova u vas ot vsego etogo vdet krugom. Dolzhen zametit',
chto predmet moej lekcii segodnya osobenno truden, no ya nadeyus', chto esli vy
budete vnimatel'no slushat' menya, to v konce koncov vam udastsya sostavit'
opredelennoe predstavlenie o haraktere teorii Diraka.
No vernemsya k teme lekcii. Tak ili inache Dirak prishel k zaklyucheniyu o
tom, chto pustoe prostranstvo do otkaza zapolneno elektronami,
raspredelennymi ravnomerno, no s beskonechno bol'shoj plotnost'yu. Kak moglo
sluchit'sya, chto my voobshche ne zamechaem stol' gustogo skopleniya elektronov i
rassmatrivaem vakuum kak absolyutnoe prostranstvo?
Vy smozhete luchshe ponyat' otvet na eti voprosy, esli voobrazite sebya
glubokovodnoj ryboj, nahodyashchejsya v tolshche vod. Ponimaet li ryba, razumeetsya,
esli ona nadelena dostatochno razvitym intellektom dlya togo, chtoby zadat'
sebe vopros, chto ona okruzhena vodoj?
|ti slova vyveli mistera Tompkinsa iz dremoty, v kotoruyu on pogruzilsya
v nachale lekcii. On byl zayadlym rybakom i dazhe pochuvstvoval na svoem lice
svezhee dyhanie morskogo vetra i voochiyu uvidel plavno katyashchiesya volny. No
hotya mister Tompkins neploho plaval, pochemu-to na etot raz emu bylo trudno
uderzhat'sya na poverhnosti i on nachal medlenno idti ko dnu, opuskayas' vse
glubzhe i glubzhe. Kak ni stranno, no on ne oshchushchal nehvatki vozduha i
chuvstvoval sebya vpolne komfortno.
- Mozhet byt', - podumal on, - so mnoj proizoshla kakaya-nibud' osobaya
recessivnaya mutaciya?
Po dannym paleontologov, zhizn' zarodilas' v okeane i pervymi, kto
vybralsya iz vody na sushu, byli tak nazyvaemye _dvoyakodyshashchie_ ryby, hodivshie
na plavnikah. Po mneniyu biologov, eti pervye dvoyakodyshashchie ryby, kotoryh
nazyvayut po-raznomu (v Avstralii rogozubami, v Afrike protopterami, v YUzhnoj
Amerike cheshujchatnikami ili lepidosirenami), postepenno prevratilis' v
suhoputnyh zhivotnyh, takih kak myshi i koshki, i v lyudej. Nekotorye iz
zhivotnyh, naprimer, kity i del'finy, oznakomivshis' so vsemi trudnostyami
zhizni na sushe, vernulis' v okean. No i posle vozvrashcheniya v vodu oni
sohranili kachestva, priobretennye vo vremya bor'by za sushchestvovanie na sushe,
naprimer, ostalis' mlekopitayushchimi, ih samki vynashivayut potomstvo vnutri
svoego tela, a ne otkladyvayut ikru, kotoruyu zatem oplodotvoryayut samcy. Razve
znamenityj vengerskij uchenyj Leo Scilard {Avtor imeet v vidu
nauchno-fantasticheskuyu novellu Leo Scilarda "Golos del'finov".} ne skazal
kak-to, chto del'finy obladayut bolee razvitym intellektom, chem lyudi?
Tut razmyshleniya mistera Tompkinsa byli prervany razgovorom,
proishodivshim gde-to gluboko pod poverhnost'yu okeana mezhdu del'finom i
tipichnym gomo sapiensom, v kotorom Tompkins (po nekogda vidennoj fotografii)
srazu uznal fizika iz Kembridzhskogo universiteta Polya Adriena Morisa Diraka.
- Poslushaj, Pol', - govoril del'fin, - ty schitaesh', chto my nahodimsya ne
v vakuume, a v material'noj srede, sostoyashchej iz chastic s otricatel'noj
massoj. YA lichno schitayu, chto voda nichem ne otlichaetsya ot pustogo
prostranstva. Ona sovershenno odnorodna, i smogu svobodno dvigat'sya v nej po
vsem napravleniyam. Odnako ot svoego dalekogo predka -
pra-pra-pra-pra-pradedushki - ya slyshal legendu o tom, chto na sushe vse inache.
Tam est' gory i ushchel'ya, preodolet' kotorye stoit nemalyh usilij. Zdes', v
vode, ya mogu dvigat'sya v lyubuyu storonu, kuda zahochu.
 - Esli govorit' o morskoj vode, to vy pravy, drug moj, - otvechal P.A.M.
- Voda sozdaet trenie o poverhnost' vashego tela, i esli vy ne budete dvigat'
hvostom i plavnikami, to ne smozhete dvigat'sya voobshche. Krome togo, poskol'ku
davlenie vody izmenyaetsya s glubinoj, vy mozhete vsplyvat' ili pogruzhat'sya,
rasshiryaya ili szhimaya svoe telo. No esli by voda ne byla vyazkoj i ne sozdavala
treniya o poverhnost' vashego tela i esli by ne bylo gradienta davleniya, to vy
byli by stol' zhe bespomoshchny, kak astronavt, u kotorogo issyaklo raketnoe
toplivo. Moj okean, sostoyashchij iz elektronov s otricatel'nymi massami,
absolyutno lishen vyazkosti i poetomu nenablyudaem. Fizicheskie pribory pozvolyayut
nablyudat' tol'ko _otsutstvie_ odnogo iz elektronov, tak kak otsutstvie
otricatel'nogo elektricheskogo zaryada ekvivalentno prisutstviyu polozhitel'nogo
elektricheskogo zaryada, poetomu dazhe Kulon mog by zametit', chto odnogo
elektrona ne hvataet.
Odnako pri sravnenii moego okeana elektronov s obychnym okeanom sleduet
imet' v vidu odno vazhnoe otlichie, chtoby eta analogiya ne zavela nas slishkom
daleko. Delo v tom, chto elektrony, obrazuyushchie moj okean, podchinyayutsya
principu Pauli. Ni odnogo elektrona nevozmozhno dobavit' k okeanu, esli vse
vozmozhnye kvantovye sostoyaniya zapolneny. Takoj "lishnij" elektron vynuzhden
byl by ostat'sya nad poverhnost'yu moego okeana i legko mog by byt' obnaruzhen
eksperimentatorami. |lektrony byli vpervye otkryty serom Dzh. Dzh. Tomsonom.
|lektrony, kotorye vrashchayutsya vokrug atomnyh yader ili letyat v vakuumnyh
trubkah, kak raz i prinadlezhat k chislu takih "lishnih" elektronov. Do togo
kak ya opublikoval svoyu pervuyu rabotu v 1930 g., ostal'noe prostranstvo
schitalos' pustym. Po obshchemu mneniyu, fizicheskoj real'nost'yu obladali togda
tol'ko sluchajnye vspleski, vzdymayushchiesya nad poverhnost'yu energii.
- No esli vash okean nenablyudaem, - zametil del'fin, - iz-za svoej
nepreryvnosti i otsutstviya treniya, to kakoj smysl tolkovat' o nem?
- Smysl est', da eshche kakoj! - vozrazil P.A.M. - Predpolozhim, chto
kakaya-to vneshnyaya sila podnyala odin iz elektronov s otricatel'noj massoj iz
glubin okeana nad ego poverhnost'yu. CHislo nablyudaemyh elektronov pri etom
uvelichilos' na edinicu, chto mozhno rassmatrivat' kak narushenie zakona
sohraneniya energii. No i pustaya dyrka v okeane, obrazovavshayasya v tom meste,
otkuda byl izvlechen elektron, takzhe budet nablyudaema, poskol'ku otsutstvie
otricatel'nogo zaryada v ravnomernom raspredelenii vosprinimaetsya, kak
prisutstvie ravnogo po velichine polozhitel'nogo zaryada. |ta polozhitel'no
zaryazhennaya chastica budet k tomu zhe obladat' polozhitel'noj massoj, i
napravlenie ee dvizheniya budet sovladat' s napravleniem sily tyazhesti.
- Vy hotite skazat', chto dyrka, ili polozhitel'no zaryazhennaya chastica,
budet vsplyvat', a ne tonut'? - s udivleniem sprosil del'fin.
- Sovershenno verno. Ne somnevayus', chto vam prihodilos' neodnokratno
videt', kak razlichnye predmety opuskayutsya na dno, uvlekaemye siloj tyazhesti,
inogda eto byli predmety, broshennye za bort s sudna, inogda sami suda.
- No poslushajte, - prerval samogo sebya P.A.M. - Vidite eti krohotnye
serebristye predmety, podnimayushchiesya k poverhnosti? Ih dvizhenie takzhe
obuslovleno dejstviem sily tyazhesti, no dvizhutsya oni v protivopolozhnuyu
storonu.
- No ved' eto zhe puzyr'ki, - zametil del'fin. - Oni, dolzhno byt',
otorvalis' ot chego-to, chto soderzhalo vozduh, kogda ono perevernulos' ili
razbilos', udarivshis' o kamenistoe dno.
- Vy sovershenno pravy, eto dejstvitel'no puzyr'ki, no ved' vam ne
prihodilos' videt', chtoby puzyr'ki vsplyvali v vakuume? Sledovatel'no, moj
okean ne pust.
- CHto i govorit', teoriya ochen' ostroumna, - soglasilsya del'fin, -
tol'ko verna li ona?
- Kogda ya predlozhil ee v 1930 g., - otvetil P.A.M., - nikto v nee ne
poveril. V znachitel'noj mere v etom nedoverii byl vinovat ya sam, poskol'ku
pervonachal'no predpolagal, chto polozhitel'no zaryazhennye chasticy predstavlyayut
soboj ne chto inoe, kak horosho izvestnye eksperimentatoram protony. Vy,
konechno, znaete, chto proton v 1840 raz tyazhelee elektrona, no ya togda pital
nadezhdu na to, chto s pomoshch'yu odnogo matematicheskogo tryuka mne udastsya
ob座asnit' vozrosshee soprotivlenie uskoreniyu pod dejstviem dannoj sily i
poluchit' chislo 1840 teoreticheski. No iz moej zatei nichego ne vyshlo, i
material'naya massa puzyr'kov v moem okeane okazalas' v tochnosti ravnoj masse
obychnogo elektrona. Moj kollega Pauli, kotoromu ya ne mogu otkazat' v chuvstve
yumora, nosilsya s ideej togo, chto on nazyval "Vtorym Principom Pauli". Po ego
vychisleniyam vyhodilo, chto esli obychnyj elektron priblizitsya k dyrke,
obrazovavshejsya pri izvlechenii odnogo elektrona iz moego okeana, to za
nichtozhno maloe vremya on zapolnit soboj dyrku. Sledovatel'no, esli proton
atoma vodoroda dejstvitel'no byl by "dyrkoj", to obrashchayushchijsya vokrug nego
elektron mgnovenno zapolnil by etu dyrku, i obe chasticy annigilirovali by so
vspyshkoj sveta, ili, luchshe skazat', so vspyshkoj gamma-izlucheniya. To zhe samoe
proizoshlo by i s atomami vseh drugih elementov. Vtoroj Princip Pauli
treboval takzhe, chtoby lyubaya vydvinutaya fizikom teoriya byla primenima i k
materii, iz kotoroj sostoit telo samogo fizika, poetomu ya annigiliroval by
prezhde, chem uspel by povedat' svoyu ideyu komu-nibud' eshche. Vot tak!
I s etimi slovami P.A.M. ischez, ispustiv yarkuyu vspyshku sveta.
- Ser, - poslyshalsya nad uhom mistera Tompkinsa chej-to razdrazhennyj
golos, - vy mozhete skol'ko ugodno spat' na lekcii, esli vam tak nravitsya, no
ne hrapite tak gromko! YA ne mogu rasslyshat' ni slova iz togo, chto govorit
professor.
Otkryv glaza, mister Tompkins uvidel snova perepolnennuyu lekcionnuyu
auditoriyu i starogo professora, kotoryj prodolzhal:
- Posmotrim, chto proizojdet, kogda stranstvuyushchaya dyrka vstrechaet na
svoem puti lishnij elektron, zanyatyj poiskom mestechka poudobnee v okeane
Diraka. YAsno, chto v rezul'tate takoj vstrechi lishnij elektron neizbezhno
svalitsya v dyrku, zapolnit ee i udivlennyj fizik, nablyudaya etot process,
otmetit yavlenie _vzaimnoj annigilyacii_ polozhitel'nogo i otricatel'nogo
elektronov. Vysvobodivshayasya pri padenii elektrona v dyrku energiya
ispuskaetsya v vide korotkovolnovogo izlucheniya i predstavlyaet soboj lish'
ostatok ot dvuh elektronov, poglotivshih drug druga, kak dva volka iz
izvestnoj detskoj skazki.
No mozhno predstavit' sebe i obratnyj process, v kotorom para chastic,
sostoyashchaya iz otricatel'nogo i polozhitel'nogo elektronov, rozhdaetsya iz nichego
pod dejstviem moshchnogo vneshnego izlucheniya. S tochki zreniya teorii Diraka,
rozhdenie pary predstavlyaet soboj prosto vybivanie elektrona iz nepreryvnogo
raspredeleniya, i rassmatrivat' ego sledovalo by ne kak rozhdenie, a kak
razdelenie dvuh protivopolozhnyh po znaku elektricheskih zaryadov. Na risunke,
kotoryj ya sejchas pokazhu vam (s. 205), eti dva processa rozhdeniya i
unichtozheniya elektronov izobrazheny ves'ma uslovno i shematichno, no, kak vy
vidite, nichego zagadochnogo v nih net. Dolzhen zametit', chto hotya process
rozhdeniya pary, strogo govorya, dolzhen proishodit' v absolyutnom vakuume,
veroyatnost' ego ochen' mala. Mozhno skazat', chto raspredelenie elektronov v
vakuume slishkom gladko, chtoby raspast'sya. S drugoj storony, v prisutstvii
tyazhelyh material'nyh chastic, sluzhashchih tochkoj shory dlya gamma-izlucheniya,
vnedryayushchegosya v raspredelenie elektronov, veroyatnost' rozhdeniya pary sil'no
vozrastaet, i process stanovitsya nablyudaemym.
- Esli govorit' o morskoj vode, to vy pravy, drug moj, - otvechal P.A.M.
- Voda sozdaet trenie o poverhnost' vashego tela, i esli vy ne budete dvigat'
hvostom i plavnikami, to ne smozhete dvigat'sya voobshche. Krome togo, poskol'ku
davlenie vody izmenyaetsya s glubinoj, vy mozhete vsplyvat' ili pogruzhat'sya,
rasshiryaya ili szhimaya svoe telo. No esli by voda ne byla vyazkoj i ne sozdavala
treniya o poverhnost' vashego tela i esli by ne bylo gradienta davleniya, to vy
byli by stol' zhe bespomoshchny, kak astronavt, u kotorogo issyaklo raketnoe
toplivo. Moj okean, sostoyashchij iz elektronov s otricatel'nymi massami,
absolyutno lishen vyazkosti i poetomu nenablyudaem. Fizicheskie pribory pozvolyayut
nablyudat' tol'ko _otsutstvie_ odnogo iz elektronov, tak kak otsutstvie
otricatel'nogo elektricheskogo zaryada ekvivalentno prisutstviyu polozhitel'nogo
elektricheskogo zaryada, poetomu dazhe Kulon mog by zametit', chto odnogo
elektrona ne hvataet.
Odnako pri sravnenii moego okeana elektronov s obychnym okeanom sleduet
imet' v vidu odno vazhnoe otlichie, chtoby eta analogiya ne zavela nas slishkom
daleko. Delo v tom, chto elektrony, obrazuyushchie moj okean, podchinyayutsya
principu Pauli. Ni odnogo elektrona nevozmozhno dobavit' k okeanu, esli vse
vozmozhnye kvantovye sostoyaniya zapolneny. Takoj "lishnij" elektron vynuzhden
byl by ostat'sya nad poverhnost'yu moego okeana i legko mog by byt' obnaruzhen
eksperimentatorami. |lektrony byli vpervye otkryty serom Dzh. Dzh. Tomsonom.
|lektrony, kotorye vrashchayutsya vokrug atomnyh yader ili letyat v vakuumnyh
trubkah, kak raz i prinadlezhat k chislu takih "lishnih" elektronov. Do togo
kak ya opublikoval svoyu pervuyu rabotu v 1930 g., ostal'noe prostranstvo
schitalos' pustym. Po obshchemu mneniyu, fizicheskoj real'nost'yu obladali togda
tol'ko sluchajnye vspleski, vzdymayushchiesya nad poverhnost'yu energii.
- No esli vash okean nenablyudaem, - zametil del'fin, - iz-za svoej
nepreryvnosti i otsutstviya treniya, to kakoj smysl tolkovat' o nem?
- Smysl est', da eshche kakoj! - vozrazil P.A.M. - Predpolozhim, chto
kakaya-to vneshnyaya sila podnyala odin iz elektronov s otricatel'noj massoj iz
glubin okeana nad ego poverhnost'yu. CHislo nablyudaemyh elektronov pri etom
uvelichilos' na edinicu, chto mozhno rassmatrivat' kak narushenie zakona
sohraneniya energii. No i pustaya dyrka v okeane, obrazovavshayasya v tom meste,
otkuda byl izvlechen elektron, takzhe budet nablyudaema, poskol'ku otsutstvie
otricatel'nogo zaryada v ravnomernom raspredelenii vosprinimaetsya, kak
prisutstvie ravnogo po velichine polozhitel'nogo zaryada. |ta polozhitel'no
zaryazhennaya chastica budet k tomu zhe obladat' polozhitel'noj massoj, i
napravlenie ee dvizheniya budet sovladat' s napravleniem sily tyazhesti.
- Vy hotite skazat', chto dyrka, ili polozhitel'no zaryazhennaya chastica,
budet vsplyvat', a ne tonut'? - s udivleniem sprosil del'fin.
- Sovershenno verno. Ne somnevayus', chto vam prihodilos' neodnokratno
videt', kak razlichnye predmety opuskayutsya na dno, uvlekaemye siloj tyazhesti,
inogda eto byli predmety, broshennye za bort s sudna, inogda sami suda.
- No poslushajte, - prerval samogo sebya P.A.M. - Vidite eti krohotnye
serebristye predmety, podnimayushchiesya k poverhnosti? Ih dvizhenie takzhe
obuslovleno dejstviem sily tyazhesti, no dvizhutsya oni v protivopolozhnuyu
storonu.
- No ved' eto zhe puzyr'ki, - zametil del'fin. - Oni, dolzhno byt',
otorvalis' ot chego-to, chto soderzhalo vozduh, kogda ono perevernulos' ili
razbilos', udarivshis' o kamenistoe dno.
- Vy sovershenno pravy, eto dejstvitel'no puzyr'ki, no ved' vam ne
prihodilos' videt', chtoby puzyr'ki vsplyvali v vakuume? Sledovatel'no, moj
okean ne pust.
- CHto i govorit', teoriya ochen' ostroumna, - soglasilsya del'fin, -
tol'ko verna li ona?
- Kogda ya predlozhil ee v 1930 g., - otvetil P.A.M., - nikto v nee ne
poveril. V znachitel'noj mere v etom nedoverii byl vinovat ya sam, poskol'ku
pervonachal'no predpolagal, chto polozhitel'no zaryazhennye chasticy predstavlyayut
soboj ne chto inoe, kak horosho izvestnye eksperimentatoram protony. Vy,
konechno, znaete, chto proton v 1840 raz tyazhelee elektrona, no ya togda pital
nadezhdu na to, chto s pomoshch'yu odnogo matematicheskogo tryuka mne udastsya
ob座asnit' vozrosshee soprotivlenie uskoreniyu pod dejstviem dannoj sily i
poluchit' chislo 1840 teoreticheski. No iz moej zatei nichego ne vyshlo, i
material'naya massa puzyr'kov v moem okeane okazalas' v tochnosti ravnoj masse
obychnogo elektrona. Moj kollega Pauli, kotoromu ya ne mogu otkazat' v chuvstve
yumora, nosilsya s ideej togo, chto on nazyval "Vtorym Principom Pauli". Po ego
vychisleniyam vyhodilo, chto esli obychnyj elektron priblizitsya k dyrke,
obrazovavshejsya pri izvlechenii odnogo elektrona iz moego okeana, to za
nichtozhno maloe vremya on zapolnit soboj dyrku. Sledovatel'no, esli proton
atoma vodoroda dejstvitel'no byl by "dyrkoj", to obrashchayushchijsya vokrug nego
elektron mgnovenno zapolnil by etu dyrku, i obe chasticy annigilirovali by so
vspyshkoj sveta, ili, luchshe skazat', so vspyshkoj gamma-izlucheniya. To zhe samoe
proizoshlo by i s atomami vseh drugih elementov. Vtoroj Princip Pauli
treboval takzhe, chtoby lyubaya vydvinutaya fizikom teoriya byla primenima i k
materii, iz kotoroj sostoit telo samogo fizika, poetomu ya annigiliroval by
prezhde, chem uspel by povedat' svoyu ideyu komu-nibud' eshche. Vot tak!
I s etimi slovami P.A.M. ischez, ispustiv yarkuyu vspyshku sveta.
- Ser, - poslyshalsya nad uhom mistera Tompkinsa chej-to razdrazhennyj
golos, - vy mozhete skol'ko ugodno spat' na lekcii, esli vam tak nravitsya, no
ne hrapite tak gromko! YA ne mogu rasslyshat' ni slova iz togo, chto govorit
professor.
Otkryv glaza, mister Tompkins uvidel snova perepolnennuyu lekcionnuyu
auditoriyu i starogo professora, kotoryj prodolzhal:
- Posmotrim, chto proizojdet, kogda stranstvuyushchaya dyrka vstrechaet na
svoem puti lishnij elektron, zanyatyj poiskom mestechka poudobnee v okeane
Diraka. YAsno, chto v rezul'tate takoj vstrechi lishnij elektron neizbezhno
svalitsya v dyrku, zapolnit ee i udivlennyj fizik, nablyudaya etot process,
otmetit yavlenie _vzaimnoj annigilyacii_ polozhitel'nogo i otricatel'nogo
elektronov. Vysvobodivshayasya pri padenii elektrona v dyrku energiya
ispuskaetsya v vide korotkovolnovogo izlucheniya i predstavlyaet soboj lish'
ostatok ot dvuh elektronov, poglotivshih drug druga, kak dva volka iz
izvestnoj detskoj skazki.
No mozhno predstavit' sebe i obratnyj process, v kotorom para chastic,
sostoyashchaya iz otricatel'nogo i polozhitel'nogo elektronov, rozhdaetsya iz nichego
pod dejstviem moshchnogo vneshnego izlucheniya. S tochki zreniya teorii Diraka,
rozhdenie pary predstavlyaet soboj prosto vybivanie elektrona iz nepreryvnogo
raspredeleniya, i rassmatrivat' ego sledovalo by ne kak rozhdenie, a kak
razdelenie dvuh protivopolozhnyh po znaku elektricheskih zaryadov. Na risunke,
kotoryj ya sejchas pokazhu vam (s. 205), eti dva processa rozhdeniya i
unichtozheniya elektronov izobrazheny ves'ma uslovno i shematichno, no, kak vy
vidite, nichego zagadochnogo v nih net. Dolzhen zametit', chto hotya process
rozhdeniya pary, strogo govorya, dolzhen proishodit' v absolyutnom vakuume,
veroyatnost' ego ochen' mala. Mozhno skazat', chto raspredelenie elektronov v
vakuume slishkom gladko, chtoby raspast'sya. S drugoj storony, v prisutstvii
tyazhelyh material'nyh chastic, sluzhashchih tochkoj shory dlya gamma-izlucheniya,
vnedryayushchegosya v raspredelenie elektronov, veroyatnost' rozhdeniya pary sil'no
vozrastaet, i process stanovitsya nablyudaemym.
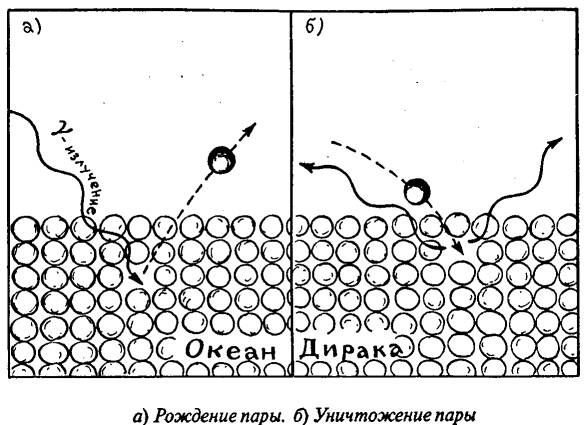 YAsno, chto pozitrony, rozhdennye opisannym vyshe obrazom, ne mogut
sushchestvovat' ochen' dolgo i vskore annigiliruyut pri vstreche s odnim iz
otricatel'nyh elektronov, obladayushchih v nashem ugolke Vselennoj bol'shim
chislennym preimushchestvom. Imenno etim ob座asnyaetsya sravnitel'no pozdnee
otkrytie takih zamechatel'nyh chastic, kak pozitrony: pervoe soobshchenie o
polozhitel'no zaryazhennyh elektronah bylo sdelano lish' v avguste 1932 g.
(teoriya Diraka byla opublikovana v 1930 g.) kalifornijskim fizikom Karlom
Andersonom, kotoryj, zanimayas' issledovaniem kosmicheskogo izlucheniya,
obnaruzhil chasticy, vo vseh otnosheniyah napominavshih obychnye elektrony, no
imevshih odno vazhnoe otlichie: vmesto otricatel'nogo zaryada eti chasticy nesli
polozhitel'nyj zaryad. Vskore posle otkrytiya Andersona my nauchilis' ochen'
prosto poluchat' elektron-pozitronnye pary v laboratornyh usloviyah, propuskaya
skvoz' kakoe-nibud' veshchestvo moshchnyj potok vysokochastotnogo izlucheniya
(radioaktivnogo gamma-izlucheniya).
YAsno, chto pozitrony, rozhdennye opisannym vyshe obrazom, ne mogut
sushchestvovat' ochen' dolgo i vskore annigiliruyut pri vstreche s odnim iz
otricatel'nyh elektronov, obladayushchih v nashem ugolke Vselennoj bol'shim
chislennym preimushchestvom. Imenno etim ob座asnyaetsya sravnitel'no pozdnee
otkrytie takih zamechatel'nyh chastic, kak pozitrony: pervoe soobshchenie o
polozhitel'no zaryazhennyh elektronah bylo sdelano lish' v avguste 1932 g.
(teoriya Diraka byla opublikovana v 1930 g.) kalifornijskim fizikom Karlom
Andersonom, kotoryj, zanimayas' issledovaniem kosmicheskogo izlucheniya,
obnaruzhil chasticy, vo vseh otnosheniyah napominavshih obychnye elektrony, no
imevshih odno vazhnoe otlichie: vmesto otricatel'nogo zaryada eti chasticy nesli
polozhitel'nyj zaryad. Vskore posle otkrytiya Andersona my nauchilis' ochen'
prosto poluchat' elektron-pozitronnye pary v laboratornyh usloviyah, propuskaya
skvoz' kakoe-nibud' veshchestvo moshchnyj potok vysokochastotnogo izlucheniya
(radioaktivnogo gamma-izlucheniya).
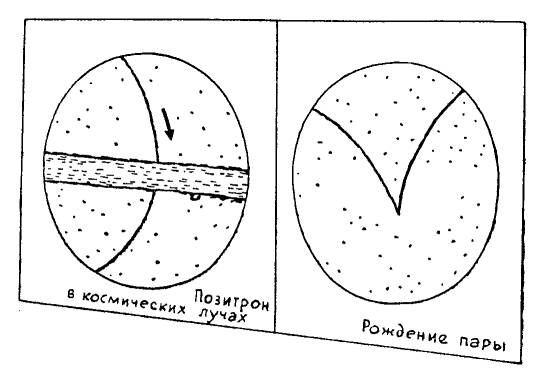 Na sleduyushchem slajde, kotoryj ya hochu pokazat' vam, vy uvidite snimki
pozitronov, obnaruzhennyh v kosmicheskom izluchenii s pomoshch'yu kamery Vil'sona,
i samogo processa rozhdeniya pary. Kamera Vil'sona - odin iz samyh poleznyh
priborov sovremennoj eksperimental'noj fiziki. Dejstvie ee osnovano na tom,
chto lyubaya chastica s nenulevym elektricheskim zaryadom, proletaya cherez gaz,
obrazuet vdol' svoego treka mnozhestvo ionov. Esli gaz nasyshchen vodyanymi
parami, to krohotnye kapel'ki vody kondensiruyutsya na etih ionah, obrazuya
tonkij sloj tumana, tyanushchijsya vdol' vsego treka. Osveshchaya etu polosku tumana
sil'nym puchkom sveta na temnom fone, my poluchaem velikolepnye kartiny, na
kotoryh otchetlivo razlichimy vse detali dvizheniya.
Na pervoj iz dvuh kartinok, sproecirovannyh na ekran, vy vidite
original snimka pozitrona, obnaruzhennogo Andersonom v kosmicheskom izluchenii.
Zamechu, chto eto samyj pervyj iz kogda-libo sdelannyh snimkov pozitrona.
SHirokaya gorizontal'naya polosa, idushchaya cherez ves' snimok, - sled tolstoj
svincovoj plastiny, polozhennoj poperek kamery Vil'sona, a trek pozitrona
vyglyadit, kak tonkaya iskrivlennaya carapina, idushchaya cherez snimok. Trek
iskrivlen potomu, chto vo vremya eksperimenta kamera Vil'sona byla pomeshchena v
sil'noe magnitnoe pole, vliyavshee na dvizhenie pozitrona. Svincovaya plastina i
magnitnoe pole ponadobilis' Andersonu dlya togo, chtoby opredelit' znak
elektricheskogo zaryada, perenosimogo chasticej. Sdelat' eto mozhno na osnove
sleduyushchih soobrazhenij. Izvestno, chto proizvodimoe magnitnym polem izgibanie
traektorii zavisit ot znaka zaryada dvizhushchejsya chasticy. V eksperimente
Andersona magnit raspolozhen tak, chto otricatel'no zaryazhennye elektrony
otklonyayutsya ot pervonachal'nogo napravleniya dvizheniya vlevo, a polozhitel'no
zaryazhennye elektrony - vpravo. Sledovatel'no, esli chastica na snimke
dvigalas' vverh, to ona dolzhna byla nesti otricatel'nyj zaryad. No kak
uznat', v kakuyu storonu dvigalas' chastica? Dlya etogo i ponadobilas'
Andersonu svincovaya plastina. Projdya skvoz' svincovuyu plastinu, chastica
neizbezhno teryaet nekuyu chast' svoej pervonachal'noj energii, i poetomu
izgibayushchee dejstvie magnitnogo polya usilivaetsya. Na snimke, kotoryj vy
vidite na slajde, trek izognut sil'nee pod svincovoj plastinoj (razlichie v
izgibah ne slishkom vidno na glaz, no otchetlivo zametno pri izmerenii).
Sledovatel'no, chastica dvigalas' sverhu vniz i nesla polozhitel'nyj zaryad.
Na pravom snimke (s. 206), poluchennom Dzhejmsom CHedvikom iz
Kembridzhskogo universiteta, vy vidite rozhdenie pary v kamere Vil'sona.
Sil'noe gamma-izluchenie postupaet v kameru snizu i, ne ostavlyaya na snimke
vidimyh sledov, porozhdaet v centre kamery paru chastic, kotorye razletayutsya v
sil'nom magnitnom pole v raznye storony. Glyadya na etot snimok, vy mozhete
gadat', pochemu pozitron (na snimke on sleva) ne annigiliruet na svoem puti
cherez gaz. Otvet na etot vopros takzhe daet teoriya Diraka, i etot otvet
ponyaten kazhdomu, kto igraet v gol'f. Esli, postaviv shar na travyanoe pole, vy
udarite po nemu slishkom sil'no, to shar ne popadet v lunku, dazhe esli vy
tochno pricelilis'. Proizojdet nechto inoe: bystro dvizhushchijsya shar prosto
pereprygnet cherez lunku i pokatitsya dal'she. Tochno tak zhe bystro dvizhushchijsya
pozitron ne popadet v dyrku Diraka, pokuda ego skorost' sushchestvenno ne
umen'shitsya. Poetomu pozitron imeet bol'shuyu veroyatnost' annigilirovat' v
konce traektorii, kogda stolknoveniya s drugimi chasticami po doroge
osnovatel'no zamedlyat ego. I, kak pokazyvayut tshchatel'nye nablyudeniya,
izluchenie, soprovozhdayushchee lyuboj process annigilyacii, dejstvitel'no
obnaruzhivaetsya v konce traektorii pozitrona. V etom - eshche odno podtverzhdenie
teorii Diraka.
Nam ostaetsya eshche obsudit' dva obshchih voprosa. Do sih por ya rassmatrival
otricatel'no zaryazhennye elektrony kak lishnie bryzgi perepolnennogo okeana
Diraka, a pozitrony - kak dyrki v nem. No vpolne dopustima i protivopolozhnaya
tochka zreniya, soglasno kotoroj obychnye elektrony nadlezhit rassmatrivat' kak
dyrki, a pozitrony - kak vybroshennye chasticy. Dlya etogo nam neobhodimo lish'
predpolozhit', chto okean Diraka ne perepolnyaetsya, a, naoborot, vsegda
ispytyvaet nedostatok chastic. V etom sluchae raspredelenie Diraka mozhno
naglyadno predstavit' kak nechto napominayushchee kusok shvejcarskogo syra s
mnozhestvom dyr v nem. Iz-za obshchej nehvatki chastic dyrki budut sushchestvovat'
vsegda, i dazhe esli kakaya-nibud' chastica okazhetsya vybroshennoj iz
raspredeleniya, ona vskore snova upadet v odnu iz dyrok. Sleduet skazat',
odnako, chto kak s fizicheskoj, tak i s matematicheskoj tochki zreniya obe
kartiny absolyutno ekvivalentny, i poetomu sovershenno bezrazlichno, kakoj iz
kartin my otdadim predpochtenie.
Vtoroe zamechanie mozhno sformulirovat' v vide sleduyushchego voprosa: "Esli
v toj chasti Vselennoj, gde my obitaem, sushchestvuet yavnoe chislennoe
preobladanie otricatel'no zaryazhennyh elektronov, to mozhno li predpolozhit',
chto gde-to v drugoj chasti Vselennoj chislennoe preimushchestvo nablyudaetsya za
polozhitel'no zaryazhennymi elektronami?" Inache govorya, kompensiruetsya li
perepolnenie okeana Diraka v nashej okrestnosti nedostatkom otricatel'no
zaryazhennyh elektronov gde-to v drugom meste?
Otvetit' na etot chrezvychajno interesnyj vopros ochen' trudno.
Dejstvitel'no, tak kak atomy, sostoyashchie iz polozhitel'no zaryazhennyh
elektronov, kotorye obrashchayutsya vokrug otricatel'no zaryazhennogo yadra, davali
by takie zhe opticheskie kartiny, kak i obychnye atomy, ne sushchestvuet sposoba
otvetit' na etot vopros s pomoshch'yu spektroskopicheskih nablyudenij. Sudya po
vsemu, chto my znaem, vpolne vozmozhno, chto obrazovanie veshchestva gde-nibud' v
Tumannosti Andromedy proishodit "naoborot" po otnosheniyu k privychnoj dlya nas
sheme, no edinstvennyj sposob podtverdit' ili oprovergnut' podobnuyu dogadku
sostoit v tom, chtoby razdobyt' kusochek togo veshchestva i proverit', ne
annigiliruet li ono pri soprikosnovenii s zemnym veshchestvom. Razumeetsya, v
sluchae annigilyacii posleduet uzhasnyj vzryv! V poslednee vremya stali
pogovarivat' o tom, chto nekotorye meteority, vzorvavshiesya pri vhozhdenii v
zemnuyu atmosferu, vozmozhno, sostoyali iz takogo "perevernutogo" veshchestva, no
ya ne dumayu, chtoby podobnye razgovory sledovalo prinimat' vser'ez. Ne
isklyucheno, chto vopros o perepolnenii okeana Diraka v odnih chastyah Vselennoj
i nehvatke chastic v drugih ee chastyah navsegda ostanetsya bez otveta.
Glava 15
Mister Tompkins znakomitsya s yaponskoj kuhnej
Odnazhdy Mod otpravilas' na vyhodnoj navestit' tetushku v Jorkshire, i
mister Tompkins priglasil professora otobedat' s nim v znamenitom yaponskom
restorane. Raspolozhivshis' na myagkih podushkah za nizkim stolikom, oni
probovali delikatesy yaponskoj kuhni i potyagivali iz chashechek sake.
- Skazhite, pozhalujsta, - obratilsya k professoru mister Tompkins, -
doktor Tallerkin upomyanul v svoej lekcii, chto protony i nejtrony
uderzhivayutsya v yadre osobymi silami scepleniya. |to te samye sily, kotorye
uderzhivayut elektrony v atome?
- O, net! - vozrazil professor. - YAdernye sily predstavlyayut soboj nechto
sovershenno drugoe. Atomnye elektrony prityagivayutsya k yadru obychnymi
elektrostaticheskimi silami, vpervye podrobno issledovannymi francuzskim
fizikom SHarlem Opostenom de Kulonom v konce XVIII veka. |to sravnitel'no
slabye sily, ubyvayushchie obratno proporcional'no kvadratu rasstoyaniya ot
centra. YAdernye sily imeyut sovershenno inuyu prirodu. Kogda proton i nejtron
sblizhayutsya vplotnuyu, no ne soprikasayutsya, to mezhdu nimi yadernye sily
prakticheski ne dejstvuyut. No kak tol'ko chasticy vhodyat v pryamoj kontakt,
mezhdu nimi voznikaet neobychajno moshchnaya sila, kotoraya uderzhivaet ih vmeste. V
etom smysle proton i nejtron napominayut dva kusochka lipkoj lenty, kotorye ne
prityagivayut drug druga dazhe na malyh rasstoyaniyah, no stanovyatsya
nerazluchnymi, kak brat'ya, stoit lish' im soprikosnut'sya. Fiziki nazvali sily,
uderzhivayushchie protony i nejtrony v yadre, _sil'nym vzaimodejstviem_. |ti sily
ne zavisyat ot elektricheskogo zaryada dvuh chastic i s odinakovoj
intensivnost'yu dejstvuyut i mezhdu dvumya nejtronami, i mezhdu protonom i
nejtronom, i mezhdu dvumya protonami.
- Sushchestvuyut li kakie-nibud' teorii, ob座asnyayushchie sil'noe
vzaimodejstvie? - sprosil mister Tompkins.
- Sushchestvuyut. V nachale 30-h godov yaponskij fizik Hideki YUkava vyskazal
gipotezu o tom, chto sil'noe vzaimodejstvie obuslovleno obmenom kakoj-to
neizvestnoj chasticej mezhdu dvumya nuklonami (nuklon - eto sobiratel'noe
nazvanie protona i nejtrona). Kogda dva nuklona sblizhayutsya, mezhdu nimi tuda
i obratno nachinayut prygat' kakie-to zagadochnye chasticy, chto i privodit k
vozniknoveniyu sil'noj svyazi, uderzhivayushchej nuklony vmeste. YUkave udalos'
teoreticheski ocenit' massu gipoteticheskih chastic. Okazalos', chto ona
primerno v 200 raz bol'she massy elektrona, ili primerno v 10 raz men'she
massy protona ili nejtrona. Takie chasticy poluchili nazvanie _mezatronov_. No
otec Vernera Gejzenberga, byvshij professorom klassicheskih yazykov, vozrazil
protiv stol' grubogo narusheniya drevnegrecheskogo yazyka. Delo v tom, chto
nazvanie _elektron_ proishodit ot grecheskogo ῆλεκτρον (yantar'), a nazvanie
_proton_ proishodit ot grecheskogo πρῶτον (pervyj). Nazvanie zhe chasticy YUkavy
bylo obrazovano ot grecheskogo μέσον (seredina), v kotorom net bukvy ρ.
Vystupiv na Mezhdunarodnoj konferencii fizikov, Gejzenberg-otec predlozhil
zamenit' nazvanie mezatron na mezon. Nekotorye francuzskie fiziki vozrazhali
potomu, chto nesmotrya na drugoe napisanie novoe nazvanie zvuchit, kak
francuzskoe slovo maison (dom, domashnij ochag). Odnako ih dovody ne byli
prinyaty vo vnimanie kollegami iz drugih stran, i novyj termin prochno
ukorenilsya v yadernoj fizike. No vzglyanite na scenu. Sejchas nam pokazhut
mezonnoe predstavlenie!
Dejstvitel'no, na scene poyavilis' shest' gejsh, kotorye nachali igrat' v
bil'boke: v kazhdoj ruke u gejsh bylo po chashke i oni lovko perebrasyvali sharik
iz odnoj chashki v druguyu i obratno. Mezhdu tem na zadnem plane poyavilsya
muzhchina i zapel:
Na sleduyushchem slajde, kotoryj ya hochu pokazat' vam, vy uvidite snimki
pozitronov, obnaruzhennyh v kosmicheskom izluchenii s pomoshch'yu kamery Vil'sona,
i samogo processa rozhdeniya pary. Kamera Vil'sona - odin iz samyh poleznyh
priborov sovremennoj eksperimental'noj fiziki. Dejstvie ee osnovano na tom,
chto lyubaya chastica s nenulevym elektricheskim zaryadom, proletaya cherez gaz,
obrazuet vdol' svoego treka mnozhestvo ionov. Esli gaz nasyshchen vodyanymi
parami, to krohotnye kapel'ki vody kondensiruyutsya na etih ionah, obrazuya
tonkij sloj tumana, tyanushchijsya vdol' vsego treka. Osveshchaya etu polosku tumana
sil'nym puchkom sveta na temnom fone, my poluchaem velikolepnye kartiny, na
kotoryh otchetlivo razlichimy vse detali dvizheniya.
Na pervoj iz dvuh kartinok, sproecirovannyh na ekran, vy vidite
original snimka pozitrona, obnaruzhennogo Andersonom v kosmicheskom izluchenii.
Zamechu, chto eto samyj pervyj iz kogda-libo sdelannyh snimkov pozitrona.
SHirokaya gorizontal'naya polosa, idushchaya cherez ves' snimok, - sled tolstoj
svincovoj plastiny, polozhennoj poperek kamery Vil'sona, a trek pozitrona
vyglyadit, kak tonkaya iskrivlennaya carapina, idushchaya cherez snimok. Trek
iskrivlen potomu, chto vo vremya eksperimenta kamera Vil'sona byla pomeshchena v
sil'noe magnitnoe pole, vliyavshee na dvizhenie pozitrona. Svincovaya plastina i
magnitnoe pole ponadobilis' Andersonu dlya togo, chtoby opredelit' znak
elektricheskogo zaryada, perenosimogo chasticej. Sdelat' eto mozhno na osnove
sleduyushchih soobrazhenij. Izvestno, chto proizvodimoe magnitnym polem izgibanie
traektorii zavisit ot znaka zaryada dvizhushchejsya chasticy. V eksperimente
Andersona magnit raspolozhen tak, chto otricatel'no zaryazhennye elektrony
otklonyayutsya ot pervonachal'nogo napravleniya dvizheniya vlevo, a polozhitel'no
zaryazhennye elektrony - vpravo. Sledovatel'no, esli chastica na snimke
dvigalas' vverh, to ona dolzhna byla nesti otricatel'nyj zaryad. No kak
uznat', v kakuyu storonu dvigalas' chastica? Dlya etogo i ponadobilas'
Andersonu svincovaya plastina. Projdya skvoz' svincovuyu plastinu, chastica
neizbezhno teryaet nekuyu chast' svoej pervonachal'noj energii, i poetomu
izgibayushchee dejstvie magnitnogo polya usilivaetsya. Na snimke, kotoryj vy
vidite na slajde, trek izognut sil'nee pod svincovoj plastinoj (razlichie v
izgibah ne slishkom vidno na glaz, no otchetlivo zametno pri izmerenii).
Sledovatel'no, chastica dvigalas' sverhu vniz i nesla polozhitel'nyj zaryad.
Na pravom snimke (s. 206), poluchennom Dzhejmsom CHedvikom iz
Kembridzhskogo universiteta, vy vidite rozhdenie pary v kamere Vil'sona.
Sil'noe gamma-izluchenie postupaet v kameru snizu i, ne ostavlyaya na snimke
vidimyh sledov, porozhdaet v centre kamery paru chastic, kotorye razletayutsya v
sil'nom magnitnom pole v raznye storony. Glyadya na etot snimok, vy mozhete
gadat', pochemu pozitron (na snimke on sleva) ne annigiliruet na svoem puti
cherez gaz. Otvet na etot vopros takzhe daet teoriya Diraka, i etot otvet
ponyaten kazhdomu, kto igraet v gol'f. Esli, postaviv shar na travyanoe pole, vy
udarite po nemu slishkom sil'no, to shar ne popadet v lunku, dazhe esli vy
tochno pricelilis'. Proizojdet nechto inoe: bystro dvizhushchijsya shar prosto
pereprygnet cherez lunku i pokatitsya dal'she. Tochno tak zhe bystro dvizhushchijsya
pozitron ne popadet v dyrku Diraka, pokuda ego skorost' sushchestvenno ne
umen'shitsya. Poetomu pozitron imeet bol'shuyu veroyatnost' annigilirovat' v
konce traektorii, kogda stolknoveniya s drugimi chasticami po doroge
osnovatel'no zamedlyat ego. I, kak pokazyvayut tshchatel'nye nablyudeniya,
izluchenie, soprovozhdayushchee lyuboj process annigilyacii, dejstvitel'no
obnaruzhivaetsya v konce traektorii pozitrona. V etom - eshche odno podtverzhdenie
teorii Diraka.
Nam ostaetsya eshche obsudit' dva obshchih voprosa. Do sih por ya rassmatrival
otricatel'no zaryazhennye elektrony kak lishnie bryzgi perepolnennogo okeana
Diraka, a pozitrony - kak dyrki v nem. No vpolne dopustima i protivopolozhnaya
tochka zreniya, soglasno kotoroj obychnye elektrony nadlezhit rassmatrivat' kak
dyrki, a pozitrony - kak vybroshennye chasticy. Dlya etogo nam neobhodimo lish'
predpolozhit', chto okean Diraka ne perepolnyaetsya, a, naoborot, vsegda
ispytyvaet nedostatok chastic. V etom sluchae raspredelenie Diraka mozhno
naglyadno predstavit' kak nechto napominayushchee kusok shvejcarskogo syra s
mnozhestvom dyr v nem. Iz-za obshchej nehvatki chastic dyrki budut sushchestvovat'
vsegda, i dazhe esli kakaya-nibud' chastica okazhetsya vybroshennoj iz
raspredeleniya, ona vskore snova upadet v odnu iz dyrok. Sleduet skazat',
odnako, chto kak s fizicheskoj, tak i s matematicheskoj tochki zreniya obe
kartiny absolyutno ekvivalentny, i poetomu sovershenno bezrazlichno, kakoj iz
kartin my otdadim predpochtenie.
Vtoroe zamechanie mozhno sformulirovat' v vide sleduyushchego voprosa: "Esli
v toj chasti Vselennoj, gde my obitaem, sushchestvuet yavnoe chislennoe
preobladanie otricatel'no zaryazhennyh elektronov, to mozhno li predpolozhit',
chto gde-to v drugoj chasti Vselennoj chislennoe preimushchestvo nablyudaetsya za
polozhitel'no zaryazhennymi elektronami?" Inache govorya, kompensiruetsya li
perepolnenie okeana Diraka v nashej okrestnosti nedostatkom otricatel'no
zaryazhennyh elektronov gde-to v drugom meste?
Otvetit' na etot chrezvychajno interesnyj vopros ochen' trudno.
Dejstvitel'no, tak kak atomy, sostoyashchie iz polozhitel'no zaryazhennyh
elektronov, kotorye obrashchayutsya vokrug otricatel'no zaryazhennogo yadra, davali
by takie zhe opticheskie kartiny, kak i obychnye atomy, ne sushchestvuet sposoba
otvetit' na etot vopros s pomoshch'yu spektroskopicheskih nablyudenij. Sudya po
vsemu, chto my znaem, vpolne vozmozhno, chto obrazovanie veshchestva gde-nibud' v
Tumannosti Andromedy proishodit "naoborot" po otnosheniyu k privychnoj dlya nas
sheme, no edinstvennyj sposob podtverdit' ili oprovergnut' podobnuyu dogadku
sostoit v tom, chtoby razdobyt' kusochek togo veshchestva i proverit', ne
annigiliruet li ono pri soprikosnovenii s zemnym veshchestvom. Razumeetsya, v
sluchae annigilyacii posleduet uzhasnyj vzryv! V poslednee vremya stali
pogovarivat' o tom, chto nekotorye meteority, vzorvavshiesya pri vhozhdenii v
zemnuyu atmosferu, vozmozhno, sostoyali iz takogo "perevernutogo" veshchestva, no
ya ne dumayu, chtoby podobnye razgovory sledovalo prinimat' vser'ez. Ne
isklyucheno, chto vopros o perepolnenii okeana Diraka v odnih chastyah Vselennoj
i nehvatke chastic v drugih ee chastyah navsegda ostanetsya bez otveta.
Glava 15
Mister Tompkins znakomitsya s yaponskoj kuhnej
Odnazhdy Mod otpravilas' na vyhodnoj navestit' tetushku v Jorkshire, i
mister Tompkins priglasil professora otobedat' s nim v znamenitom yaponskom
restorane. Raspolozhivshis' na myagkih podushkah za nizkim stolikom, oni
probovali delikatesy yaponskoj kuhni i potyagivali iz chashechek sake.
- Skazhite, pozhalujsta, - obratilsya k professoru mister Tompkins, -
doktor Tallerkin upomyanul v svoej lekcii, chto protony i nejtrony
uderzhivayutsya v yadre osobymi silami scepleniya. |to te samye sily, kotorye
uderzhivayut elektrony v atome?
- O, net! - vozrazil professor. - YAdernye sily predstavlyayut soboj nechto
sovershenno drugoe. Atomnye elektrony prityagivayutsya k yadru obychnymi
elektrostaticheskimi silami, vpervye podrobno issledovannymi francuzskim
fizikom SHarlem Opostenom de Kulonom v konce XVIII veka. |to sravnitel'no
slabye sily, ubyvayushchie obratno proporcional'no kvadratu rasstoyaniya ot
centra. YAdernye sily imeyut sovershenno inuyu prirodu. Kogda proton i nejtron
sblizhayutsya vplotnuyu, no ne soprikasayutsya, to mezhdu nimi yadernye sily
prakticheski ne dejstvuyut. No kak tol'ko chasticy vhodyat v pryamoj kontakt,
mezhdu nimi voznikaet neobychajno moshchnaya sila, kotoraya uderzhivaet ih vmeste. V
etom smysle proton i nejtron napominayut dva kusochka lipkoj lenty, kotorye ne
prityagivayut drug druga dazhe na malyh rasstoyaniyah, no stanovyatsya
nerazluchnymi, kak brat'ya, stoit lish' im soprikosnut'sya. Fiziki nazvali sily,
uderzhivayushchie protony i nejtrony v yadre, _sil'nym vzaimodejstviem_. |ti sily
ne zavisyat ot elektricheskogo zaryada dvuh chastic i s odinakovoj
intensivnost'yu dejstvuyut i mezhdu dvumya nejtronami, i mezhdu protonom i
nejtronom, i mezhdu dvumya protonami.
- Sushchestvuyut li kakie-nibud' teorii, ob座asnyayushchie sil'noe
vzaimodejstvie? - sprosil mister Tompkins.
- Sushchestvuyut. V nachale 30-h godov yaponskij fizik Hideki YUkava vyskazal
gipotezu o tom, chto sil'noe vzaimodejstvie obuslovleno obmenom kakoj-to
neizvestnoj chasticej mezhdu dvumya nuklonami (nuklon - eto sobiratel'noe
nazvanie protona i nejtrona). Kogda dva nuklona sblizhayutsya, mezhdu nimi tuda
i obratno nachinayut prygat' kakie-to zagadochnye chasticy, chto i privodit k
vozniknoveniyu sil'noj svyazi, uderzhivayushchej nuklony vmeste. YUkave udalos'
teoreticheski ocenit' massu gipoteticheskih chastic. Okazalos', chto ona
primerno v 200 raz bol'she massy elektrona, ili primerno v 10 raz men'she
massy protona ili nejtrona. Takie chasticy poluchili nazvanie _mezatronov_. No
otec Vernera Gejzenberga, byvshij professorom klassicheskih yazykov, vozrazil
protiv stol' grubogo narusheniya drevnegrecheskogo yazyka. Delo v tom, chto
nazvanie _elektron_ proishodit ot grecheskogo ῆλεκτρον (yantar'), a nazvanie
_proton_ proishodit ot grecheskogo πρῶτον (pervyj). Nazvanie zhe chasticy YUkavy
bylo obrazovano ot grecheskogo μέσον (seredina), v kotorom net bukvy ρ.
Vystupiv na Mezhdunarodnoj konferencii fizikov, Gejzenberg-otec predlozhil
zamenit' nazvanie mezatron na mezon. Nekotorye francuzskie fiziki vozrazhali
potomu, chto nesmotrya na drugoe napisanie novoe nazvanie zvuchit, kak
francuzskoe slovo maison (dom, domashnij ochag). Odnako ih dovody ne byli
prinyaty vo vnimanie kollegami iz drugih stran, i novyj termin prochno
ukorenilsya v yadernoj fizike. No vzglyanite na scenu. Sejchas nam pokazhut
mezonnoe predstavlenie!
Dejstvitel'no, na scene poyavilis' shest' gejsh, kotorye nachali igrat' v
bil'boke: v kazhdoj ruke u gejsh bylo po chashke i oni lovko perebrasyvali sharik
iz odnoj chashki v druguyu i obratno. Mezhdu tem na zadnem plane poyavilsya
muzhchina i zapel:
 For a meson I received the Nobel Prize,
An achievement I prefer to minimize.
Lambda zero, Yokohama,
Eta keon, Fujiyama -
For a meson I received the Nobel Prize.
They proposed to call it Yukon in Japan,
I demurred, for I'm a very modest man.
Lambda zero, Yokohama,
Eta keon, Fujiyama -
They proposed to call it Yukon in Japan.
(Za mezon ya poluchil Nobelevskuyu premiyu,
No hotel by, chtoby ob etom pomen'she shumeli.
Lyambda nol', Iokogama,
|ta kaon, Fudziyama -
Za mezon ya poluchil Nobelevskuyu premiyu.
V YAponii mezon predpochitayut nazyvat' yukonom,
YA protivlyus' etomu, tak kak chelovek ya ochen' skromnyj.
Lyambda nol', Iokogama,
|ta kaon, Fudziyama -
V YAponii mezon predpochitayut nazyvat' yukonom.)
- A pochemu vystupayut tri pary gejsh? - sprosil mister Tompkins.
- Oni izobrazhayut tri vozmozhnyh varianta obmena mezonami, - poyasnil
professor. - Mezony byvayut treh tipov: polozhitel'no zaryazhennye, otricatel'no
zaryazhennye i elektricheski nejtral'nye. Vozmozhno, chto yadernye sily porozhdeny
mezonami vseh treh tipov.
- Itak, nyne sushchestvuyut vosem' elementarnyh chastic, - podvel itog svoim
razmyshleniyam mister Tompkins i prinyalsya schitat' na pal'cah, - nejtrony,
protony (polozhitel'no i otricatel'no zaryazhennye), polozhitel'no i
otricatel'no zaryazhennye elektrony i mezony treh sortov.
- Net! - voskliknul professor. - |lementarnyh chastic sejchas izvestno ne
vosem', a blizhe k vos'midesyati. Snachala vyyasnilos', chto sushchestvuyut dve
raznovidnosti mezonov, tyazhelye i legkie. Tyazhelye mezony fiziki oboznachili
grecheskoj bukvoj pi i nazvali _pionami_, a legkie - grecheskoj bukvoj myu i
nazvali _myuonami_. Piony rozhdayutsya na granice atmosfery pri stolknovenii
protonov ochen' vysokoj energii s yadrami gazov, obrazuyushchih vozduh. No piony
ochen' nestabil'ny i raspadayutsya, prezhde chem dostignut poverhnosti Zemli, na
myuony i nejtrino (samye zagadochnye iz vseh chastic), kotorye ne obladayut ni
massoj, ni zaryadom, a tol'ko perenosyat energiyu. Myuony zhivut neskol'ko
dol'she, okolo neskol'kih mikrosekund, poetomu oni uspevayut dostignut'
poverhnosti Zemli i raspadayutsya na nashih glazah na obychnyj elektron i dva
nejtrino. Sushchestvuyut takzhe chasticy, oboznachaemye grecheskoj bukvoj ka i
nazyvaemye _kaonami_.
- A kakie iz chastic ispol'zuyut eti gejshi v svoej igre? -
pointeresovalsya mister Tompkins.
- Po-vidimomu, piony, skoree vsego nejtral'nye (oni igrayut naibolee
vazhnuyu rol'), no ya ne vpolne uveren. Bol'shinstvo novyh chastic, otkryvaemyh
nyne pochti kazhdyj mesyac, nastol'ko korotkozhivushchie, dazhe esli oni dvizhutsya so
skorost'yu sveta, chto raspadayutsya na rasstoyanii neskol'kih santimetrov ot
mesta rozhdeniya, i poetomu dazhe chuvstvitel'nye pribory, zapuskaemye v
atmosferu na sharah, "ne zamechayut" ih.
No teper' u nas est' moshchnye uskoriteli chastic, sposobnye razgonyat'
protony do stol' zhe vysokih energij, kakie te dostigayut v kosmicheskom
izluchenii, t. e. do mnogih tysyach millionov elektron-vol't. Odna iz etih
mashin pod nazvaniem lourenstron raspolozhena zdes' nepodaleku, blizhe k
vershine holma, i ya budu rad pokazat' ee vam.
For a meson I received the Nobel Prize,
An achievement I prefer to minimize.
Lambda zero, Yokohama,
Eta keon, Fujiyama -
For a meson I received the Nobel Prize.
They proposed to call it Yukon in Japan,
I demurred, for I'm a very modest man.
Lambda zero, Yokohama,
Eta keon, Fujiyama -
They proposed to call it Yukon in Japan.
(Za mezon ya poluchil Nobelevskuyu premiyu,
No hotel by, chtoby ob etom pomen'she shumeli.
Lyambda nol', Iokogama,
|ta kaon, Fudziyama -
Za mezon ya poluchil Nobelevskuyu premiyu.
V YAponii mezon predpochitayut nazyvat' yukonom,
YA protivlyus' etomu, tak kak chelovek ya ochen' skromnyj.
Lyambda nol', Iokogama,
|ta kaon, Fudziyama -
V YAponii mezon predpochitayut nazyvat' yukonom.)
- A pochemu vystupayut tri pary gejsh? - sprosil mister Tompkins.
- Oni izobrazhayut tri vozmozhnyh varianta obmena mezonami, - poyasnil
professor. - Mezony byvayut treh tipov: polozhitel'no zaryazhennye, otricatel'no
zaryazhennye i elektricheski nejtral'nye. Vozmozhno, chto yadernye sily porozhdeny
mezonami vseh treh tipov.
- Itak, nyne sushchestvuyut vosem' elementarnyh chastic, - podvel itog svoim
razmyshleniyam mister Tompkins i prinyalsya schitat' na pal'cah, - nejtrony,
protony (polozhitel'no i otricatel'no zaryazhennye), polozhitel'no i
otricatel'no zaryazhennye elektrony i mezony treh sortov.
- Net! - voskliknul professor. - |lementarnyh chastic sejchas izvestno ne
vosem', a blizhe k vos'midesyati. Snachala vyyasnilos', chto sushchestvuyut dve
raznovidnosti mezonov, tyazhelye i legkie. Tyazhelye mezony fiziki oboznachili
grecheskoj bukvoj pi i nazvali _pionami_, a legkie - grecheskoj bukvoj myu i
nazvali _myuonami_. Piony rozhdayutsya na granice atmosfery pri stolknovenii
protonov ochen' vysokoj energii s yadrami gazov, obrazuyushchih vozduh. No piony
ochen' nestabil'ny i raspadayutsya, prezhde chem dostignut poverhnosti Zemli, na
myuony i nejtrino (samye zagadochnye iz vseh chastic), kotorye ne obladayut ni
massoj, ni zaryadom, a tol'ko perenosyat energiyu. Myuony zhivut neskol'ko
dol'she, okolo neskol'kih mikrosekund, poetomu oni uspevayut dostignut'
poverhnosti Zemli i raspadayutsya na nashih glazah na obychnyj elektron i dva
nejtrino. Sushchestvuyut takzhe chasticy, oboznachaemye grecheskoj bukvoj ka i
nazyvaemye _kaonami_.
- A kakie iz chastic ispol'zuyut eti gejshi v svoej igre? -
pointeresovalsya mister Tompkins.
- Po-vidimomu, piony, skoree vsego nejtral'nye (oni igrayut naibolee
vazhnuyu rol'), no ya ne vpolne uveren. Bol'shinstvo novyh chastic, otkryvaemyh
nyne pochti kazhdyj mesyac, nastol'ko korotkozhivushchie, dazhe esli oni dvizhutsya so
skorost'yu sveta, chto raspadayutsya na rasstoyanii neskol'kih santimetrov ot
mesta rozhdeniya, i poetomu dazhe chuvstvitel'nye pribory, zapuskaemye v
atmosferu na sharah, "ne zamechayut" ih.
No teper' u nas est' moshchnye uskoriteli chastic, sposobnye razgonyat'
protony do stol' zhe vysokih energij, kakie te dostigayut v kosmicheskom
izluchenii, t. e. do mnogih tysyach millionov elektron-vol't. Odna iz etih
mashin pod nazvaniem lourenstron raspolozhena zdes' nepodaleku, blizhe k
vershine holma, i ya budu rad pokazat' ee vam.
 Posle neprodolzhitel'noj poezdki na avtomashine professor i mister
Tompkins pod容hali k ogromnomu zdaniyu, vnutri kotorogo nahodilsya uskoritel'.
Vojdya v zdanie, mister Tompkins byl potryasen slozhnost'yu gigantskogo
sooruzheniya. No po zavereniyu professora, uskoritel' v principe byl ne bolee
slozhen, chem prashcha, iz kotoroj David ubil Goliafa. Zaryazhennye chasticy
inzhektirovalis' (postupali) v centre gigantskogo barabana i, dvigayas' po
raskruchivayushchimsya spiralyam, uskoryalis' peremennymi elektricheskimi impul'sami.
Dvizheniem chastic upravlyaet sil'noe magnitnoe pole.
- Mne kazhetsya, ya uzhe videl nechto podobnoe, - skazal mister Tompkins, -
kogda neskol'ko let nazad posetil ciklotron, kotoryj nazyvalsya "atomnoj
drobilkoj".
- Vy sovershenno pravy, - podtverdil professor. - Ciklotron, kotoryj vy
togda videli, byl izobreten doktorom Lourensom. Uskoritel', kotoryj vy
vidite zdes', osnovan na tom zhe principe, no on mozhet razgonyat' chasticy uzhe
ne do neskol'kih millionov elektron-vol't, a do mnogih tysyach millionov
elektron-vol't. Dva takih uskoritelya byli nedavno sooruzheny v Soedinennyh
SHtatah. Odin iz nih nahoditsya v Berkli (shtat Kaliforniya) i nazyvaetsya
_bevatron_, poskol'ku razgonyaet chasticy do energij v milliardy
elektron-vol't. |to chisto amerikanskoe nazvanie, tak kak tol'ko v Amerike
tysyachu millionov prinyato nazyvat' billionom. V Velikobritanii billionom
nazyvaetsya million millionov, i nikto v dobroj staroj Anglii eshche ne pytalsya
dostich' stol' vysokih energij. Drugoj amerikanskij uskoritel' chastic
nahoditsya v Brukhejvene, Long-Ajlend, i nazyvaetsya _kosmotron_. |to nazvanie
neskol'ko pretenciozno, tak kak energii, dostizhimye v kosmicheskom izluchenii,
chasto namnogo prevyshayut te, do kotoryh razgonyaet chasticy kosmotron. V
Evrope, v Evropejskom centre yadernyh issledovanij (CERN) bliz ZHenevy,
postroeny uskoriteli, sravnimye s dvumya amerikanskimi uskoritelyami. V
Rossii, nedaleko ot Moskvy, postroen eshche odin uskoritel' takogo zhe tipa,
obshcheizvestnyj pod nazvaniem _hrushchevtron_. Vozmozhno, chto teper' on budet
pereimenovan v _brezhnevtron_.
Oglyadevshis' po storonam, mister Tompkins obratil vnimanie na dver', na
kotoroj krasovalas' nadpis':
Posle neprodolzhitel'noj poezdki na avtomashine professor i mister
Tompkins pod容hali k ogromnomu zdaniyu, vnutri kotorogo nahodilsya uskoritel'.
Vojdya v zdanie, mister Tompkins byl potryasen slozhnost'yu gigantskogo
sooruzheniya. No po zavereniyu professora, uskoritel' v principe byl ne bolee
slozhen, chem prashcha, iz kotoroj David ubil Goliafa. Zaryazhennye chasticy
inzhektirovalis' (postupali) v centre gigantskogo barabana i, dvigayas' po
raskruchivayushchimsya spiralyam, uskoryalis' peremennymi elektricheskimi impul'sami.
Dvizheniem chastic upravlyaet sil'noe magnitnoe pole.
- Mne kazhetsya, ya uzhe videl nechto podobnoe, - skazal mister Tompkins, -
kogda neskol'ko let nazad posetil ciklotron, kotoryj nazyvalsya "atomnoj
drobilkoj".
- Vy sovershenno pravy, - podtverdil professor. - Ciklotron, kotoryj vy
togda videli, byl izobreten doktorom Lourensom. Uskoritel', kotoryj vy
vidite zdes', osnovan na tom zhe principe, no on mozhet razgonyat' chasticy uzhe
ne do neskol'kih millionov elektron-vol't, a do mnogih tysyach millionov
elektron-vol't. Dva takih uskoritelya byli nedavno sooruzheny v Soedinennyh
SHtatah. Odin iz nih nahoditsya v Berkli (shtat Kaliforniya) i nazyvaetsya
_bevatron_, poskol'ku razgonyaet chasticy do energij v milliardy
elektron-vol't. |to chisto amerikanskoe nazvanie, tak kak tol'ko v Amerike
tysyachu millionov prinyato nazyvat' billionom. V Velikobritanii billionom
nazyvaetsya million millionov, i nikto v dobroj staroj Anglii eshche ne pytalsya
dostich' stol' vysokih energij. Drugoj amerikanskij uskoritel' chastic
nahoditsya v Brukhejvene, Long-Ajlend, i nazyvaetsya _kosmotron_. |to nazvanie
neskol'ko pretenciozno, tak kak energii, dostizhimye v kosmicheskom izluchenii,
chasto namnogo prevyshayut te, do kotoryh razgonyaet chasticy kosmotron. V
Evrope, v Evropejskom centre yadernyh issledovanij (CERN) bliz ZHenevy,
postroeny uskoriteli, sravnimye s dvumya amerikanskimi uskoritelyami. V
Rossii, nedaleko ot Moskvy, postroen eshche odin uskoritel' takogo zhe tipa,
obshcheizvestnyj pod nazvaniem _hrushchevtron_. Vozmozhno, chto teper' on budet
pereimenovan v _brezhnevtron_.
Oglyadevshis' po storonam, mister Tompkins obratil vnimanie na dver', na
kotoroj krasovalas' nadpis':
ZHIDKIJ VODOROD ALXVARESA
VANNOE OTDELENIE
- A chto za etoj dver'yu? - sprosil on.
- O! - otvetil professor. - Vidite li, lourenstron proizvodit vse
bol'she i bol'she razlichnyh elementarnyh chastic vse bol'shej i bol'shej energii.
Ih prihoditsya analizirovat', nablyudaya traektorii i vychislyaya massy, vremena
zhizni, vzaimodejstviya i mnogie drugie svojstva, takie kak strannost',
chetnost' i t. d. V davnie vremena dlya nablyudeniya traektorij ispol'zovalas'
tak nazyvaemaya kamera Vil'sona, za sozdanie kotoroj CH. T. R. Vil'son v 1927
g. poluchil Nobelevskuyu premiyu. V to vremya bystrye elektricheski zaryazhennye
chasticy s energiej v neskol'ko millionov elektron-vol't, issleduemye
fizikami, propuskalis' cherez kameru so steklyannoj kryshkoj, napolnennuyu
vozduhom, pochti do predela nasyshchennym vodyanymi parami. Kogda dno kamery
rezko opuskalos', vozduh vsledstvie rasshireniya ohlazhdalsya i vodyanoj par
stanovilsya _perenasyshchennym_. V rezul'tate nekotoraya dolya para
kondensirovalas' v krohotnye vodyanye kapel'ki. Vil'son obnaruzhil, chto takaya
kondensaciya parov v vodu proishodit gorazdo bystree vokrug ionov, t. e.
elektricheski zaryazhennyh chastic gaza. No vdol' traektorij elektricheski
zaryazhennyh chastic, proletayushchih skvoz' kameru, gaz ioniziruetsya. V rezul'tate
neprozrachnye poloski tumana, osveshchaemye istochnikom sveta, raspolozhennym na
stenke kamery, stanovyatsya vidimymi na vykrashennom v chernyj cvet dne kamery.
Vspomnite snimki, kotorye ya pokazyval vam na proshloj lekcii.
 V sluchae chastic iz kosmicheskih luchej s energiyami, tysyachekratno
prevoshodyashchimi energii chastic, kotorye my izuchali do sih por, situaciya inaya
potomu, chto treki chastic stanovyatsya ochen' dlinnymi i kamery Vil'sona,
zapolnennye vozduhom, slishkom maly dlya togo, chtoby mozhno bylo prosledit'
ves' trek chasticy ot nachala do konca, poetomu nablyudeniyu dostupna lish'
nebol'shaya chast' traektorii.
Bol'shoj shag vpered byl nedavno sdelan amerikanskim fizikom Donal'dom A.
Glezerom, kotoromu v 1960 g. byla prisuzhdena za eto Nobelevskaya premiya. Kak
rasskazyvaet sam Glezer, odnazhdy on sidel v bare i ugryumo nablyudal za
puzyr'kami, podnimavshimisya v stoyavshem pered nim bokale piva. Vnezapno emu
prishla v golovu ideya: "Esli CH. T. R. Vil'son mog izuchat' kapel'ki zhidkosti v
gaze, to pochemu by mne ne zanyat'sya izucheniem puzyr'kov gaza v zhidkosti?"
- Ne stanu vdavat'sya v tehnicheskie detali, - prodolzhal professor, - i
kasat'sya trudnostej, voznikshih na puti k tehnicheskomu voploshcheniyu idei
Glezera. Vam vse ravno oni byli by neponyatny. Skazhu tol'ko, chto dlya
nadlezhashchego funkcionirovaniya puzyr'kovoj kamery (takoe nazvanie poluchilo
izobretenie Glezera) naibolee podhodyashchej zhidkost'yu okazalsya zhidkij vodorod,
temperatura kotorogo sostavlyaet okolo dvuhsot pyatidesyati gradusov po
Farengejtu nizhe temperatury zamerzaniya vody. V sosednej komnate stoit
bol'shoj kontejner; postroennyj Luisom Al'varesom i zapolnennyj zhidkim
vodorodom. Obychno ego nazyvayut "vannoj Al'varesa".
- Br-r-r! - poezhilsya mister Tompkins. - Dlya menya holodnovato!
- Vam vovse ne nuzhno lezt' v vannu. Vpolne dostatochno nablyudat' za
traektoriyami chastic skvoz' prozrachnye stenki.
Vannaya funkcionirovala kak vsegda, i kamery so vspyshkoj, raspolozhennye
vokrug nee, nepreryvno delali snimok za snimkom. Sama vanna byla pomeshchena
vnutri bol'shogo elektromagnita, izgibavshego traektorii chastic, chtoby zatem
po izgibu eksperimentatory mogli ocenivat' skorost' ih dvizheniya.
- Proizvodstvo odnogo snimka zanimaet neskol'ko minut, - poyasnil
Al'vares. - V den' poluchaetsya do neskol'kih soten snimkov, esli ustanovka ne
vyhodit iz stroya i ne trebuet kakogo-nibud' remonta. Kazhdyj snimok
podvergaetsya tshchatel'nomu izucheniyu, vse treki analiziruyutsya, a ih krivizna
tshchatel'no izmeryaetsya. Analiz i izmereniya zanimayut ot neskol'kih minut do
chasa v zavisimosti ot togo, naskol'ko interesen snimok i naskol'ko bystro
spravlyaetsya s rabotoj devushka.
- Pochemu vy skazali "devushka"? - prerval ego mister Tompkins. - Razve
eto chisto zhenskoe zanyatie?
- Razumeetsya, net, - otvetil Al'vares. - Mnogie iz nashih devushek v
dejstvitel'nosti mal'chiki. No kogda my govorim o teh, kto zanimaetsya
obrabotkoj snimkov, to nazyvaem ih devushkami nezavisimo ot pola. Termin
"devushka" oznachaet edinicu effektivnosti i tochnosti. Kogda vy govorite
"mashinistka" ili "sekretar'", to obychno predstavlyaete sebe zhenshchinu, a ne
muzhchinu. Tak vot, dlya analiza vseh snimkov, poluchaemyh v nashej laboratorii,
nam ponadobilis' by sotni devushek, chto prevratilos' by v nelegkuyu problemu.
Poetomu my rassylaem mnozhestvo nashih snimkov v drugie universitety, ne
imeyushchie dostatochno sredstv, chtoby postroit' lourenstrony i puzyr'kovye
kamery, no raspolagayushchie summami deneg, kotoryh vpolne hvataet na pokupku
priborov dlya analiza nashih snimkov.
V sluchae chastic iz kosmicheskih luchej s energiyami, tysyachekratno
prevoshodyashchimi energii chastic, kotorye my izuchali do sih por, situaciya inaya
potomu, chto treki chastic stanovyatsya ochen' dlinnymi i kamery Vil'sona,
zapolnennye vozduhom, slishkom maly dlya togo, chtoby mozhno bylo prosledit'
ves' trek chasticy ot nachala do konca, poetomu nablyudeniyu dostupna lish'
nebol'shaya chast' traektorii.
Bol'shoj shag vpered byl nedavno sdelan amerikanskim fizikom Donal'dom A.
Glezerom, kotoromu v 1960 g. byla prisuzhdena za eto Nobelevskaya premiya. Kak
rasskazyvaet sam Glezer, odnazhdy on sidel v bare i ugryumo nablyudal za
puzyr'kami, podnimavshimisya v stoyavshem pered nim bokale piva. Vnezapno emu
prishla v golovu ideya: "Esli CH. T. R. Vil'son mog izuchat' kapel'ki zhidkosti v
gaze, to pochemu by mne ne zanyat'sya izucheniem puzyr'kov gaza v zhidkosti?"
- Ne stanu vdavat'sya v tehnicheskie detali, - prodolzhal professor, - i
kasat'sya trudnostej, voznikshih na puti k tehnicheskomu voploshcheniyu idei
Glezera. Vam vse ravno oni byli by neponyatny. Skazhu tol'ko, chto dlya
nadlezhashchego funkcionirovaniya puzyr'kovoj kamery (takoe nazvanie poluchilo
izobretenie Glezera) naibolee podhodyashchej zhidkost'yu okazalsya zhidkij vodorod,
temperatura kotorogo sostavlyaet okolo dvuhsot pyatidesyati gradusov po
Farengejtu nizhe temperatury zamerzaniya vody. V sosednej komnate stoit
bol'shoj kontejner; postroennyj Luisom Al'varesom i zapolnennyj zhidkim
vodorodom. Obychno ego nazyvayut "vannoj Al'varesa".
- Br-r-r! - poezhilsya mister Tompkins. - Dlya menya holodnovato!
- Vam vovse ne nuzhno lezt' v vannu. Vpolne dostatochno nablyudat' za
traektoriyami chastic skvoz' prozrachnye stenki.
Vannaya funkcionirovala kak vsegda, i kamery so vspyshkoj, raspolozhennye
vokrug nee, nepreryvno delali snimok za snimkom. Sama vanna byla pomeshchena
vnutri bol'shogo elektromagnita, izgibavshego traektorii chastic, chtoby zatem
po izgibu eksperimentatory mogli ocenivat' skorost' ih dvizheniya.
- Proizvodstvo odnogo snimka zanimaet neskol'ko minut, - poyasnil
Al'vares. - V den' poluchaetsya do neskol'kih soten snimkov, esli ustanovka ne
vyhodit iz stroya i ne trebuet kakogo-nibud' remonta. Kazhdyj snimok
podvergaetsya tshchatel'nomu izucheniyu, vse treki analiziruyutsya, a ih krivizna
tshchatel'no izmeryaetsya. Analiz i izmereniya zanimayut ot neskol'kih minut do
chasa v zavisimosti ot togo, naskol'ko interesen snimok i naskol'ko bystro
spravlyaetsya s rabotoj devushka.
- Pochemu vy skazali "devushka"? - prerval ego mister Tompkins. - Razve
eto chisto zhenskoe zanyatie?
- Razumeetsya, net, - otvetil Al'vares. - Mnogie iz nashih devushek v
dejstvitel'nosti mal'chiki. No kogda my govorim o teh, kto zanimaetsya
obrabotkoj snimkov, to nazyvaem ih devushkami nezavisimo ot pola. Termin
"devushka" oznachaet edinicu effektivnosti i tochnosti. Kogda vy govorite
"mashinistka" ili "sekretar'", to obychno predstavlyaete sebe zhenshchinu, a ne
muzhchinu. Tak vot, dlya analiza vseh snimkov, poluchaemyh v nashej laboratorii,
nam ponadobilis' by sotni devushek, chto prevratilos' by v nelegkuyu problemu.
Poetomu my rassylaem mnozhestvo nashih snimkov v drugie universitety, ne
imeyushchie dostatochno sredstv, chtoby postroit' lourenstrony i puzyr'kovye
kamery, no raspolagayushchie summami deneg, kotoryh vpolne hvataet na pokupku
priborov dlya analiza nashih snimkov.
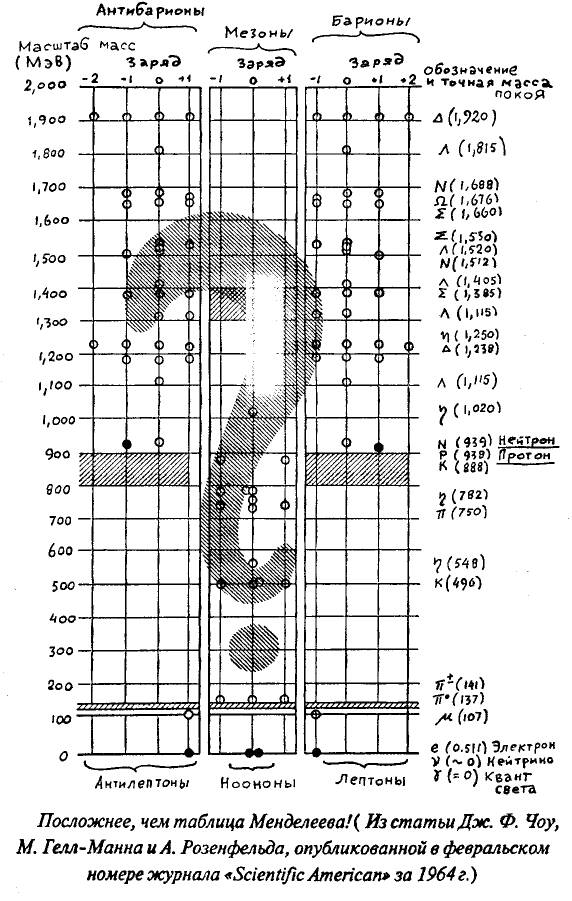 - Takogo roda snimki poluchaete tol'ko vy ili kto-nibud' eshche? -
pointeresovalsya mister Tompkins.
- Analogichnye uskoriteli imeyutsya v Brukhejvenskoj Nacional'noj
Laboratorii na Long-Ajlende v N'yu-Jorke, v CERNe (Evropejskom centre yadernyh
issledovanij) bliz ZHenevy i v Laboratorii "SHCHelkunchik" nepodaleku ot Moskvy v
Rossii. Vse eti laboratorii zanyaty poiskom igolki v stoge sena i, chto samoe
udivitel'noe, vremya ot vremeni im vse zhe udaetsya najti igolku!
- A dlya chego vedetsya eta kropotlivaya rabota? - sprosil v udivlenii
mister Tompkins.
- CHtoby iskat' i nahodit' novye elementarnye chasticy (najti kotorye,
kstati skazat', gorazdo trudnee, chem igolku v stoge sena!) i issledovat'
vzaimodejstvie mezhdu nimi. Zdes' na stene tablica izvestnyh elementarnyh
chastic i ona uzhe sejchas soderzhit bol'she chastic, chem elementov v
Periodicheskoj sisteme Mendeleeva.
- A pochemu stol' chudovishchnye usiliya predprinimayutsya lish' dlya togo, chtoby
najti novye chasticy? - prodolzhal udivlyat'sya mister Tompkins.
- Takova nauka, - otvetil professor, - popytka chelovecheskogo razuma
ponyat' vse, chto nas okruzhaet, bud' to gigantskie zvezdnye galaktiki,
mikroskopicheskie bakterii ili elementarnye chasticy. Poznavat' okruzhayushchij mir
zahvatyvayushche interesno, i poetomu my zanimaemsya etim.
- A ne sposobstvuet li razvitie nauki dostizheniyu prakticheskih celej,
uvelichivaya blagosostoyanie lyudej i delaya ih zhizn' bolee udobnoj?
- Razumeetsya, sposobstvuet, no eto lish' vtorostepennaya cel'. Ne dumaete
zhe vy, chto osnovnoe naznachenie muzyki sostoit v tom, chtoby uchit' gornistov
budit' po utram soldat, szyvat' ih na zavtraki, obedy i uzhiny ili prizyvat'
ih na bitvu? Govoryat: "Lyubopytstvo sgubilo koshku". YA govoryu:
"Lyuboznatel'nost' rozhdaet uchenogo".
S etimi slovami professor pozhelal misteru Tompkinsu spokojnoj nochi.
Zamechatel'nyj fizik-teoretik Georgij Antonovich (Dzhordzh) Gamov
(1904-1968) ne byl uzkim specialistom. On ostavil zametnyj sled v kvantovoj
mehanike, atomnoj i yadernoj fizike, astrofizike, kosmologii i biologii. Ego
idei, yarkie i original'nye, ne raz prokladyvali novye napravleniya nauchnyh
issledovanij. Emu prinadlezhat pionerskie raboty po kvantovoj teorii
al'fa-raspada i tunnel'nomu effektu, urovnyam energii v yadre, modelyam zvezd s
termoyadernymi istochnikami energii, roli nejtrino pri vspyshkah sverhnovyh i
novyh, obrazovaniyu himicheskih elementov putem zahvata nejtronov, reliktovomu
izlucheniyu i geneticheskomu kodu.
Ne menee obshirno, original'no i yarko literaturnoe nasledie G. A.
Gamova. Ego peru prinadlezhit uvlekatel'naya avtobiografiya "Moya mirovaya liniya"
i celaya rossyp' zamechatel'nyh nauchno-populyarnyh knig, takih, kak "Mister
Tompkins v Strane CHudes", "Mister Tompkins issleduet atom", "Raz, dva,
tri... beskonechnost'", "Tridcat' let, kotorye potryasli fiziku", "Sotvorenie
Vselennoj", "Biografiya fiziki", "Zvezda pod nazvaniem Solnce", "Biografiya
Zemli", "Planeta pod nazvaniem Zemlya".
Predlagaemaya vnimaniyu chitatelya kniga - pervaya publikaciya proizvedenij
G. A. Gamova na russkom yazyke.
- Takogo roda snimki poluchaete tol'ko vy ili kto-nibud' eshche? -
pointeresovalsya mister Tompkins.
- Analogichnye uskoriteli imeyutsya v Brukhejvenskoj Nacional'noj
Laboratorii na Long-Ajlende v N'yu-Jorke, v CERNe (Evropejskom centre yadernyh
issledovanij) bliz ZHenevy i v Laboratorii "SHCHelkunchik" nepodaleku ot Moskvy v
Rossii. Vse eti laboratorii zanyaty poiskom igolki v stoge sena i, chto samoe
udivitel'noe, vremya ot vremeni im vse zhe udaetsya najti igolku!
- A dlya chego vedetsya eta kropotlivaya rabota? - sprosil v udivlenii
mister Tompkins.
- CHtoby iskat' i nahodit' novye elementarnye chasticy (najti kotorye,
kstati skazat', gorazdo trudnee, chem igolku v stoge sena!) i issledovat'
vzaimodejstvie mezhdu nimi. Zdes' na stene tablica izvestnyh elementarnyh
chastic i ona uzhe sejchas soderzhit bol'she chastic, chem elementov v
Periodicheskoj sisteme Mendeleeva.
- A pochemu stol' chudovishchnye usiliya predprinimayutsya lish' dlya togo, chtoby
najti novye chasticy? - prodolzhal udivlyat'sya mister Tompkins.
- Takova nauka, - otvetil professor, - popytka chelovecheskogo razuma
ponyat' vse, chto nas okruzhaet, bud' to gigantskie zvezdnye galaktiki,
mikroskopicheskie bakterii ili elementarnye chasticy. Poznavat' okruzhayushchij mir
zahvatyvayushche interesno, i poetomu my zanimaemsya etim.
- A ne sposobstvuet li razvitie nauki dostizheniyu prakticheskih celej,
uvelichivaya blagosostoyanie lyudej i delaya ih zhizn' bolee udobnoj?
- Razumeetsya, sposobstvuet, no eto lish' vtorostepennaya cel'. Ne dumaete
zhe vy, chto osnovnoe naznachenie muzyki sostoit v tom, chtoby uchit' gornistov
budit' po utram soldat, szyvat' ih na zavtraki, obedy i uzhiny ili prizyvat'
ih na bitvu? Govoryat: "Lyubopytstvo sgubilo koshku". YA govoryu:
"Lyuboznatel'nost' rozhdaet uchenogo".
S etimi slovami professor pozhelal misteru Tompkinsu spokojnoj nochi.
Zamechatel'nyj fizik-teoretik Georgij Antonovich (Dzhordzh) Gamov
(1904-1968) ne byl uzkim specialistom. On ostavil zametnyj sled v kvantovoj
mehanike, atomnoj i yadernoj fizike, astrofizike, kosmologii i biologii. Ego
idei, yarkie i original'nye, ne raz prokladyvali novye napravleniya nauchnyh
issledovanij. Emu prinadlezhat pionerskie raboty po kvantovoj teorii
al'fa-raspada i tunnel'nomu effektu, urovnyam energii v yadre, modelyam zvezd s
termoyadernymi istochnikami energii, roli nejtrino pri vspyshkah sverhnovyh i
novyh, obrazovaniyu himicheskih elementov putem zahvata nejtronov, reliktovomu
izlucheniyu i geneticheskomu kodu.
Ne menee obshirno, original'no i yarko literaturnoe nasledie G. A.
Gamova. Ego peru prinadlezhit uvlekatel'naya avtobiografiya "Moya mirovaya liniya"
i celaya rossyp' zamechatel'nyh nauchno-populyarnyh knig, takih, kak "Mister
Tompkins v Strane CHudes", "Mister Tompkins issleduet atom", "Raz, dva,
tri... beskonechnost'", "Tridcat' let, kotorye potryasli fiziku", "Sotvorenie
Vselennoj", "Biografiya fiziki", "Zvezda pod nazvaniem Solnce", "Biografiya
Zemli", "Planeta pod nazvaniem Zemlya".
Predlagaemaya vnimaniyu chitatelya kniga - pervaya publikaciya proizvedenij
G. A. Gamova na russkom yazyke.
Last-modified: Sat, 25 Mar 2006 06:35:31 GMT




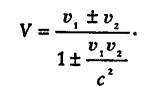

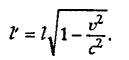
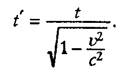
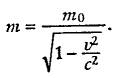




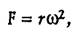
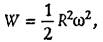
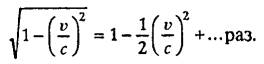
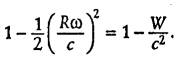
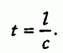
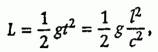
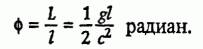
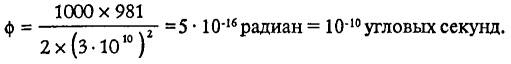
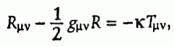









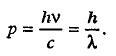
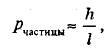



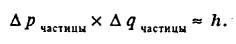
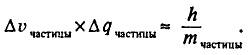
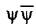 .
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej
.
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej 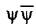 -funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
-funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono: