yu ee
dvizheniya - s pomoshch'yu matematicheskoj linii, poskol'ku v kvantovom mire vse
ob容kty rasplyvayutsya. Nam neobhodimo obratit'sya k drugim metodam opisaniya,
dayushchim, tak skazat', "plotnost' razmazni" v razlichnyh tochkah prostranstva.
Matematicheski eto oznachaet, chto my ispol'zuem nepreryvnye funkcii (takie
kak, naprimer, v gidromehanike), a fizicheski trebuet, chtoby pri opisanii
kvantovogo mira my upotreblyali takie oboroty rechi, kak "etot ob容kt v
osnovnom nahoditsya zdes', chastichno tam i dazhe von tam" ili "eta moneta na
75% nahoditsya v moem karmane i na 25% - v vashem". YA ponimayu, chto takie
utverzhdeniya kazhutsya vam dikimi, no v nashej povsednevnoj zhizni iz-za malosti
kvantovoj postoyannoj v nih net nadobnosti. No esli vy voznamerites' izuchat'
atomnuyu fiziku, to ya nastoyatel'no rekomenduyu vam predvaritel'no privyknut' k
takogo roda vyrazheniyam.
Schitayu svoim dolgom predosterech' vas ot oshibochnogo predstavleniya o tom,
budto funkciya, opisyvayushchaya "plotnost' prebyvaniya" ob容kta v razlichnyh tochkah
prostranstva, obladaet fizicheskoj real'nost'yu v nashem obychnom trehmernom
prostranstve. Dejstvitel'no, esli my opisyvaem povedenie, naprimer, dvuh
chastic, to nam neobhodimo otvetit' na vopros, nahoditsya li odna chastica v
odnom meste i, odnovremenno, vtoraya chastica v drugom meste. Dlya etogo nam
neobhodima funkciya shesti peremennyh (koordinat dvuh chastic), kotoruyu
nevozmozhno "lokalizovat'" v trehmernom prostranstve. Dlya opisaniya bolee
slozhnyh sistem nam ponadobilis' by funkcii eshche bol'shego chisla peremennyh. V
etom smysle "kvantovo-mehanicheskaya funkciya" analogichna "potencial'noj
funkcii", ili "potencialu", sistemy chastic v klassicheskoj mehanike ili
"entropii" sistemy v statisticheskoj mehanike: ona tol'ko opisyvaet dvizhenie
i pozvolyaet nam predskazyvat' rezul'tat lyubogo konkretnogo dvizheniya pri
dannyh usloviyah. Fizicheskaya real'nost' ostaetsya za chasticami, dvizhenie
kotoryh my opisyvaem.
Funkciya, kotoraya opisyvaet, kakaya "dolya" chasticy ili sistemy chastic
prisutstvuet v razlichnyh mestah prostranstva, trebuet special'nogo
matematicheskogo oboznacheniya. Sleduya |rvinu SHredingeru, kotoryj pervym
napisal uravnenie, opredelyayushchee povedenie takoj funkcii, ee stali oboznachat'
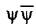 .
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej
.
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej 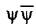 -funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
-funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
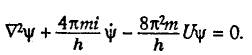 (7)
Zdes' U oznachaet potencial sil, dejstvuyushchih na nashu chasticu (s massoj
m), i porozhdaet opredelennoe reshenie zadachi o dvizhenii chasticy pri lyubom
zadannom raspredelenii sily. "Volnovoe uravnenie SHredingera" (tak prinyato
nazyvat' vyvedennoe SHredingerom fundamental'noe uravnenie) pozvolilo fizikam
v posleduyushchie sorok let ego sushchestvovaniya postroit' naibolee polnuyu i
logicheski neprotivorechivuyu kartinu yavlenij, proishodyashchih v mire atomov.
Nekotorye iz vas, dolzhno byt', udivlyayutsya, pochemu ya do sih por ni razu
ne upotrebil slovo "matrica", kotoroe chasto prihoditsya slyshat' v svyazi s
kvantovoj teoriej. Dolzhen priznat'sya, chto lichno ya pitayu sil'nuyu nepriyazn' k
matricam i predpochitayu obhodit'sya bez nih. No chtoby ne ostavlyat' vas v
absolyutnom nevedenii otnositel'no etogo matematicheskogo apparata kvantovoj
teorii, ya skazhu o matricah neskol'ko slov. Kak vy uzhe znaete, dvizhenie
chasticy ili slozhnoj mehanicheskoj sistemy vsegda mozhno opisat' s pomoshch'yu
nekotoryh nepreryvnyh volnovyh funkcij. |ti funkcii chasto byvayut ochen'
slozhnymi i predstavimy v vide nabora iz nekotorogo chisla bolee prostyh
kolebanij (tak nazyvaemyh "sobstvennyh funkcij") podobno tomu, kak slozhnyj
zvuk mozhno sostavit' iz nekotorogo chisla prostyh garmonicheskih tonov.
Slozhnoe dvizhenie mozhno opisyvat', zadavaya amplitudy ego razlichnyh komponent.
Poskol'ku chislo komponent (obertonov) beskonechno, my vypisyvaem beskonechnuyu
tablicu amplitud vida
(7)
Zdes' U oznachaet potencial sil, dejstvuyushchih na nashu chasticu (s massoj
m), i porozhdaet opredelennoe reshenie zadachi o dvizhenii chasticy pri lyubom
zadannom raspredelenii sily. "Volnovoe uravnenie SHredingera" (tak prinyato
nazyvat' vyvedennoe SHredingerom fundamental'noe uravnenie) pozvolilo fizikam
v posleduyushchie sorok let ego sushchestvovaniya postroit' naibolee polnuyu i
logicheski neprotivorechivuyu kartinu yavlenij, proishodyashchih v mire atomov.
Nekotorye iz vas, dolzhno byt', udivlyayutsya, pochemu ya do sih por ni razu
ne upotrebil slovo "matrica", kotoroe chasto prihoditsya slyshat' v svyazi s
kvantovoj teoriej. Dolzhen priznat'sya, chto lichno ya pitayu sil'nuyu nepriyazn' k
matricam i predpochitayu obhodit'sya bez nih. No chtoby ne ostavlyat' vas v
absolyutnom nevedenii otnositel'no etogo matematicheskogo apparata kvantovoj
teorii, ya skazhu o matricah neskol'ko slov. Kak vy uzhe znaete, dvizhenie
chasticy ili slozhnoj mehanicheskoj sistemy vsegda mozhno opisat' s pomoshch'yu
nekotoryh nepreryvnyh volnovyh funkcij. |ti funkcii chasto byvayut ochen'
slozhnymi i predstavimy v vide nabora iz nekotorogo chisla bolee prostyh
kolebanij (tak nazyvaemyh "sobstvennyh funkcij") podobno tomu, kak slozhnyj
zvuk mozhno sostavit' iz nekotorogo chisla prostyh garmonicheskih tonov.
Slozhnoe dvizhenie mozhno opisyvat', zadavaya amplitudy ego razlichnyh komponent.
Poskol'ku chislo komponent (obertonov) beskonechno, my vypisyvaem beskonechnuyu
tablicu amplitud vida
 (8)
Nad takimi tablicami mozhno proizvodit' matematicheskie operacii po
sravnitel'no prostym pravilam. Kazhdaya takaya tablica i nazyvaetsya "matricej",
i nekotorye fiziki vmesto togo, chtoby imet' delo neposredstvenno s volnovymi
funkciyami, predpochitayut operirovat' s matricami. Takaya "matrichnaya mehanika",
kak ee inogda nazyvayut, predstavlyaet soboj ne bolee chem matematicheskuyu
modifikaciyu obychnoj "volnovoj mehaniki". V nashih lekciyah, posvyashchennyh
glavnym obrazom principial'nym voprosam, bylo by izlishne vhodit' v eti
problemy bolee podrobno.
Ochen' zhal', chto nedostatok vremeni ne pozvolyaet mne rasskazat' vam o
dal'nejshem progresse kvantovoj teorii v svyazi s teoriej otnositel'nosti. |ta
glava v razvitii kvantovoj teorii, svyazannaya glavnym obrazom s rabotami
britanskogo fizika Polya Adriena Morisa Diraka, privodit ko mnogim
interesnejshim problemam i stala osnovoj nekotoryh chrezvychajno vazhnyh
eksperimental'nyh otkrytij. Vozmozhno, kogda-nibud' v drugoj raz ya eshche
vernus' k etim problemam, a poka ya dolzhen ostanovit'sya. Nadeyus', chto
prochitannaya mnoj seriya lekcij pozvolila vam sostavit' bolee yasnoe
predstavlenie o sovremennoj koncepcii fizicheskogo mira i probudila v vas
interes k dal'nejshim nauchnym zanyatiyam.
Glava 8
Kvantovye dzhungli
Na sleduyushchee utro mister Tompkins eshche nezhilsya v posteli, kak vdrug
pochuvstvoval, chto v komnate est' eshche kto-to. Oglyadevshis' vokrug, on
obnaruzhil svoego starogo druga professora. Tot sidel v kresle, utknuvshis' v
rasstelennuyu na kolenyah kartu i vnimatel'no izuchal ee.
- Tak vy so mnoj? - sprosil professor, podnimaya golovu.
- A kuda eto vy sobralis'? - pointeresovalsya mister Tompkins, razmyshlyaya
nad tem, kakim obrazom professor okazalsya u nego v komnate.
- Razumeetsya, dlya togo chtoby polyubovat'sya na slonov i drugih obitatelej
dzhunglej. Vladelec bil'yardnoj, gde my s vami nedavno pobyvali, soobshchil mne
po sekretu, otkuda on beret slonovuyu kost' dlya svoih bil'yardnyh sharov.
Vidite rajon, kotoryj ya obvel na karte krasnym karandashom? Imeyutsya osnovaniya
polagat', chto vnutri nego vse podchineno kvantovym zakonam s ochen' bol'shoj
kvantovoj postoyannoj. Mestnye zhiteli schitayut, chto v teh krayah poselilis'
d'yavoly, i ya boyus', chto nam budet ochen' trudno najti sebe provodnika. No
esli vy hotite otpravit'sya so mnoj v put', vam nado potoraplivat'sya. Sudno
othodit cherez chas, a nam eshche nuzhno po doroge v port zaehat' za serom
Richardom.
- A kto eto ser Richard? - sprosil mister Tompkins.
- Kak, vy nikogda ne slyhali o nem? - professor byl yavno izumlen. - Ser
Richard izvestnyj ohotnik na tigrov. On reshil otpravit'sya vmeste s nami,
kogda ya obeshchal emu interesnuyu ohotu.
Na prichal uchastniki ekspedicii pribyli kak raz vovremya dlya togo, chtoby
nablyudat' za pogruzkoj na bort sudna gruza iz neskol'kih dlinnyh yashchikov s
ruzh'yami sera Richarda i special'nymi pulyami, izgotovlennymi iz svinca,
kotoryj professor poluchil ot upravlyayushchego svincovymi rudnikami,
raspolozhennymi nepodaleku ot kvantovyh dzhunglej. Mister Tompkins eshche
raskladyval veshchi v kayute, kogda mernaya vibraciya korpusa sudna vozvestila
emu, chto parohod otoshel ot prichala. V morskom puteshestvii vsegda est' nechto
neotrazimo privlekatel'noe, i mister Tompkins ne zametil, kak ih sudno
prishvartovalos' v ocharovatel'nom vostochnom gorode - blizhajshem k tainstvennym
kvantovym dzhunglyam naselennom punkte.
- Dlya puteshestviya po sushe nam nuzhno priobresti slona, - ob座avil
professor. - Ne dumayu, chto kto-nibud' iz mestnyh zhitelej risknet otpravit'sya
s nami, poetomu upravlyat' slonom pridetsya nam samim. Polagayu, chto vy, mister
Tompkins, prekrasno spravites' s etoj zadachej. YA budu slishkom pogloshchen
nauchnymi nablyudeniyami, a ser Richard dolzhen budet upravlyat'sya so vsem
ohotnich'im snaryazheniem.
Na dushe u mistera Tompkinsa bylo ochen' nespokojno, kogda pridya na
slonovyj rynok, raspolozhennyj na okraine goroda, on uvidel ogromnyh
zhivotnyh, odnim iz kotoryh emu predstoyalo upravlyat'. Ser Richard, velikolepno
razbiravshijsya v slonah, vybral krasivogo krupnogo slona i sprosil u
vladel'ca, skol'ko tot hochet za zhivotnoe.
- Hrap hanvek o hobot ham. Hagori ho, o Hohohohi, - otvetil tuzemec,
obnazhiv v ulybke oslepitel'no belye zuby.
- On prosit za nego ujmu deneg, - perevel ser Richard, - no govorit, chto
ego slon iz kvantovyh dzhunglej i poetomu stoit dorozhe. Tak kak, kupim etogo
slona?
- Nepremenno, - skazal professor. - Na parohode mne dovelos' slyshat',
chto slony inogda zahodyat iz kvantovyh territorij i tuzemcy ih lovyat. Takie
slony gorazdo luchshe svoih sorodichej iz drugih oblastej, i sejchas nam prosto
povezlo, chto my mozhem kupit' zhivotnoe, kotoroe chuvstvuet sebya v kvantovyh
dzhunglyah, kak doma.
Mister Tompkins osmotrel slona so vseh storon. CHto i govorit', eto bylo
ochen' krasivoe, ogromnoe zhivotnoe, odnako, mister Tomtgkins ne zametil v
povadkah slona kakih-libo otlichij po sravneniyu s temi slonami, kotoryh emu
dovodilos' videt' v zooparke.
- Vy govorite, chto eto kvantovyj slon, a dlya menya on vpolne obychnyj
slon i vedet sebya ne tak zanyatno, kak bil'yardnye shary, sdelannye iz bivnej
nekotoryh iz ego sorodichej. Naprimer, pochemu on ne rasplyvaetsya po vsem
napravleniyam? - obratilsya mister Tompkins k professoru.
- Vy medlenno shvatyvaete sut' dela, - zametil professor. - Slon ne
rasplyvaetsya iz-za svoej ochen' bol'shoj massy. Nekotoroe vremya nazad ya uzhe
ob座asnyal vam, chto neopredelennost' v polozhenii i skorosti zavisit ot massy.
CHem bol'she massa, tem men'she neopredelennost'. Imenno poetomu kvantovye
zakony ne nablyudayutsya v obychnom mire dazhe dlya takih legkih tel, kak pylinki,
no stanovyatsya vpolne zametnymi dlya elektronov, kotorye v milliardy
milliardov raz legche pylinok. No v kvantovyh dzhunglyah kvantovaya postoyannaya
gorazdo bol'she, no vse zhe nedostatochno velika, chtoby porozhdat' porazitel'nye
effekty v povedenii stol' tyazhelogo zhivotnogo, kak slon. Neopredelennost' v
polozhenii kvantovogo slona mozhno zametit', tol'ko esli pristal'no vglyadet'sya
v ego ochertaniya. Vozmozhno, vy zametili, chto poverhnost' slonovoj kozhi ne
vpolne opredelenna i kazhetsya neskol'ko neotchetlivo vidimoj. So vremenem eta
neopredelennost' uvelichivaetsya ochen' medlenno. Mne kazhetsya, chto imenno s
etim obstoyatel'stvom svyazana mestnaya legenda, budto u staryh slonov iz
kvantovyh dzhunglej dlinnaya sherst'. YA polagayu, chto na ne stol' krupnyh
zhivotnyh, obitayushchih v kvantovyh dzhunglyah, zamechatel'nye kvantovye effekty
budut bolee zametnymi.
- Horosho, chto v etu ekspediciyu my otpravlyaemsya ne verhom na loshadyah, -
podumal mister Tompkins. - Ved' esli by my vzdumali otpravit'sya v kvantovye
dzhungli na loshadyah, ya nikogda ne mog by skazat' s uverennost'yu, gde moya
loshad' - u menya pod sedlom ili v sleduyushchej doline.
Posle togo, kak professor i ser Richard so svoimi ruzh'yami vzgromozdilis'
v korzinu, ukreplennuyu na spine slona, a mister Tompkins v novoj dlya sebya
dolzhnosti pogonshchika zanyal svoe mesto na shee slona, krepko szhimaya v ruke
nekoe podobie bagra - strekalo, kotorym _nastoyashchie_ pogonshchiki upravlyayut
svoim podopechnym; ekspediciya tronulas' v put' k tainstvennym dzhunglyam.
Ot zhitelej goroda nashi puteshestvenniki uznali, chto dobrat'sya do
dzhunglej mozhno primerno za chas, i mister Tompkins, izo vseh sil pytayas'
sohranit' ravnovesie mezhdu ushami slona, voznamerilsya s pol'zoj ispol'zovat'
vremya, chtoby porassprosit' u professora o kvantovyh yavleniyah.
- Skazhite, pozhalujsta, - nachal mister Tompkins, povernuvshis' k
professoru, - _pochemu_ tela s maloj massoj vedut sebya stol' neobychno i kak
mozhno istolkovat' s tochki zreniya obychnogo zdravogo smysla tu kvantovuyu
postoyannuyu, o kotoroj vy vse vremya govorite?
- O, - voskliknul professor, - ponyat' eto ne tak uzh trudno. Neobychnoe
povedenie vseh ob容ktov v kvantovom mire ob座asnyaetsya prosto tem, chto vy na
nih smotrite.
- Oni nastol'ko stydlivy? - ulybnulsya mister Tompkins.
- "Stydlivy" - ne to slovo, - surovo otvetstvoval professor. - Sut'
dela v tom, chto vsyakij raz, proizvodya lyuboe nablyudenie, vy nepremenno
vozmushchaete dvizhenie nablyudaemogo ob容kta. Raz vy uznaete chto-to o dvizhenii
kakogo-to tela, to eto oznachaet, chto dvizhushcheesya telo proizvelo kakoe-to
dejstvie na vashi organy chuvstv ili na pribor, kotoryj vy ispol'zovali pri
nablyudenii. V silu ravenstva dejstviya i protivodejstviya my prihodim k
zaklyucheniyu, chto vash izmeritel'nyj pribor takzhe vozdejstvoval na telo i, tak
skazat', "isportil" ego dvizhenie, vvedya neopredelennost' v polozhenie i
skorost' tela.
- Esli by ya tronul bil'yardnyj shar pal'cem, to, konechno, vnes by
vozmushchenie v ego dvizhenie, - nedoumenno proiznes mister Tompkins. - No ya
tol'ko posmotrel na nego. Neuzheli etogo dostatochno, chtoby vozmutit' dvizhenie
bil'yardnogo shara?
- Razumeetsya, vpolne dostatochno! Vy zhe ne mozhete videt' bil'yardnyj shar
v kromeshnoj t'me. A esli vy vynesete shar na svet, to luchi sveta,
otrazhayushchiesya ot shara i delayushchie ego vidimym, vozdejstvuyut na nego (my
govorim o takom vozdejstvii kak o "davlenii sveta") i "portyat" dvizhenie
shara.
- A chto esli ya vospol'zuyus' ochen' tonkimi i ochen' chuvstvitel'nymi
priborami? Razve ne smogu ya sdelat' vozdejstvie moih priborov na dvizhushcheesya
telo prenebrezhimo malym?
- Imenno tak my schitali, kogda u nas byla tol'ko klassicheskaya fizika,
do otkrytiya _kvanta dejstviya_. No v nachale XX stoletiya stalo yasno, chto
dejstvie na lyuboj ob容kt ne mozhet byt' nizvedeno do urovnya nizhe
opredelennogo predela, nazyvaemogo kvantovoj postoyannoj i oboznachaemogo
simvolom h. V obychnom mire kvant dejstviya ochen' mal; v obychnyh edinicah on
vyrazhaetsya chislom s dvadcat'yu sem'yu nulyami posle desyatichnoj zapyatoj. Kvant
dejstviya stanovitsya sushchestvennym tol'ko dlya takih legkih chastic, kak
elektrony: iz-za ih ochen' maloj massy na dvizhenii takih chastic zametno
skazyvayutsya i ochen' slabye vozdejstviya. V kvantovyh dzhunglyah, k kotorym my
sejchas priblizhaemsya, kvant dejstviya ochen' velik. |to grubyj mir, v kotorom
delikatnye dejstviya nevozmozhny. Esli kto-nibud' v takom mire popytaetsya
pogladit' kotenka, to tot libo voobshche ne oshchutit nikakoj laski, libo ego sheya
budet slomana pri pervom zhe prikosnovenii.
- Vse eto horosho, - zadumchivo progovoril mister Tompkins, - no vedut li
tela sebya prilichno, t.e. tak, kak obychno prinyato dumat', kogda na nih nikto
ne smotrit?
- Kogda na tela nikto ne smotrit, - otvetil professor, - nikto ne mozhet
skazat', kak oni sebya vedut. Vash vopros ne imeet fizicheskogo smysla.
- Dolzhen priznat'sya, - zametil mister Tompkins, - chto vse eto izryadno
smahivaet na filosofiyu, a ne na fiziku.
- Mozhete nazyvat' eto filosofiej, - professor byl yavno zadet, - no, v
dejstvitel'nosti, rech' idet o fundamental'nom principe sovremennoj fiziki -
_nikogda ne govorit' o tom, chego ne znaesh'_. Vsya sovremennaya fizicheskaya
teoriya osnovana na etom principe, mezhdu tem, kak filosofy obychno upuskayut
ego iz vidu. Naprimer, znamenityj nemeckij filosof Kant provel nemalo
vremeni, razmyshlyaya o svojstvah tel, ne takih, kakimi oni "vidyatsya nam", a
takih, kakie oni est' " v sebe". Dlya sovremennogo fizika imeyut smysl tol'ko
tak nazyvaemye "nablyudaemye" (t. e. principial'no nablyudaemye svojstva), i
vsya sovremennaya fizika osnovana na otnosheniyah mezhdu nablyudaemymi svojstvami.
To, chto nevozmozhno nablyudat', horosho tol'ko dlya prazdnyh razmyshlenij: vy
mozhete pridumyvat' chto ugodno, i plody vashih razmyshlenij nel'zya ni proverit'
(t. e. ubedit'sya v ih sushchestvovanii), ni vospol'zovat'sya imi. Dolzhen
skazat', chto...
(8)
Nad takimi tablicami mozhno proizvodit' matematicheskie operacii po
sravnitel'no prostym pravilam. Kazhdaya takaya tablica i nazyvaetsya "matricej",
i nekotorye fiziki vmesto togo, chtoby imet' delo neposredstvenno s volnovymi
funkciyami, predpochitayut operirovat' s matricami. Takaya "matrichnaya mehanika",
kak ee inogda nazyvayut, predstavlyaet soboj ne bolee chem matematicheskuyu
modifikaciyu obychnoj "volnovoj mehaniki". V nashih lekciyah, posvyashchennyh
glavnym obrazom principial'nym voprosam, bylo by izlishne vhodit' v eti
problemy bolee podrobno.
Ochen' zhal', chto nedostatok vremeni ne pozvolyaet mne rasskazat' vam o
dal'nejshem progresse kvantovoj teorii v svyazi s teoriej otnositel'nosti. |ta
glava v razvitii kvantovoj teorii, svyazannaya glavnym obrazom s rabotami
britanskogo fizika Polya Adriena Morisa Diraka, privodit ko mnogim
interesnejshim problemam i stala osnovoj nekotoryh chrezvychajno vazhnyh
eksperimental'nyh otkrytij. Vozmozhno, kogda-nibud' v drugoj raz ya eshche
vernus' k etim problemam, a poka ya dolzhen ostanovit'sya. Nadeyus', chto
prochitannaya mnoj seriya lekcij pozvolila vam sostavit' bolee yasnoe
predstavlenie o sovremennoj koncepcii fizicheskogo mira i probudila v vas
interes k dal'nejshim nauchnym zanyatiyam.
Glava 8
Kvantovye dzhungli
Na sleduyushchee utro mister Tompkins eshche nezhilsya v posteli, kak vdrug
pochuvstvoval, chto v komnate est' eshche kto-to. Oglyadevshis' vokrug, on
obnaruzhil svoego starogo druga professora. Tot sidel v kresle, utknuvshis' v
rasstelennuyu na kolenyah kartu i vnimatel'no izuchal ee.
- Tak vy so mnoj? - sprosil professor, podnimaya golovu.
- A kuda eto vy sobralis'? - pointeresovalsya mister Tompkins, razmyshlyaya
nad tem, kakim obrazom professor okazalsya u nego v komnate.
- Razumeetsya, dlya togo chtoby polyubovat'sya na slonov i drugih obitatelej
dzhunglej. Vladelec bil'yardnoj, gde my s vami nedavno pobyvali, soobshchil mne
po sekretu, otkuda on beret slonovuyu kost' dlya svoih bil'yardnyh sharov.
Vidite rajon, kotoryj ya obvel na karte krasnym karandashom? Imeyutsya osnovaniya
polagat', chto vnutri nego vse podchineno kvantovym zakonam s ochen' bol'shoj
kvantovoj postoyannoj. Mestnye zhiteli schitayut, chto v teh krayah poselilis'
d'yavoly, i ya boyus', chto nam budet ochen' trudno najti sebe provodnika. No
esli vy hotite otpravit'sya so mnoj v put', vam nado potoraplivat'sya. Sudno
othodit cherez chas, a nam eshche nuzhno po doroge v port zaehat' za serom
Richardom.
- A kto eto ser Richard? - sprosil mister Tompkins.
- Kak, vy nikogda ne slyhali o nem? - professor byl yavno izumlen. - Ser
Richard izvestnyj ohotnik na tigrov. On reshil otpravit'sya vmeste s nami,
kogda ya obeshchal emu interesnuyu ohotu.
Na prichal uchastniki ekspedicii pribyli kak raz vovremya dlya togo, chtoby
nablyudat' za pogruzkoj na bort sudna gruza iz neskol'kih dlinnyh yashchikov s
ruzh'yami sera Richarda i special'nymi pulyami, izgotovlennymi iz svinca,
kotoryj professor poluchil ot upravlyayushchego svincovymi rudnikami,
raspolozhennymi nepodaleku ot kvantovyh dzhunglej. Mister Tompkins eshche
raskladyval veshchi v kayute, kogda mernaya vibraciya korpusa sudna vozvestila
emu, chto parohod otoshel ot prichala. V morskom puteshestvii vsegda est' nechto
neotrazimo privlekatel'noe, i mister Tompkins ne zametil, kak ih sudno
prishvartovalos' v ocharovatel'nom vostochnom gorode - blizhajshem k tainstvennym
kvantovym dzhunglyam naselennom punkte.
- Dlya puteshestviya po sushe nam nuzhno priobresti slona, - ob座avil
professor. - Ne dumayu, chto kto-nibud' iz mestnyh zhitelej risknet otpravit'sya
s nami, poetomu upravlyat' slonom pridetsya nam samim. Polagayu, chto vy, mister
Tompkins, prekrasno spravites' s etoj zadachej. YA budu slishkom pogloshchen
nauchnymi nablyudeniyami, a ser Richard dolzhen budet upravlyat'sya so vsem
ohotnich'im snaryazheniem.
Na dushe u mistera Tompkinsa bylo ochen' nespokojno, kogda pridya na
slonovyj rynok, raspolozhennyj na okraine goroda, on uvidel ogromnyh
zhivotnyh, odnim iz kotoryh emu predstoyalo upravlyat'. Ser Richard, velikolepno
razbiravshijsya v slonah, vybral krasivogo krupnogo slona i sprosil u
vladel'ca, skol'ko tot hochet za zhivotnoe.
- Hrap hanvek o hobot ham. Hagori ho, o Hohohohi, - otvetil tuzemec,
obnazhiv v ulybke oslepitel'no belye zuby.
- On prosit za nego ujmu deneg, - perevel ser Richard, - no govorit, chto
ego slon iz kvantovyh dzhunglej i poetomu stoit dorozhe. Tak kak, kupim etogo
slona?
- Nepremenno, - skazal professor. - Na parohode mne dovelos' slyshat',
chto slony inogda zahodyat iz kvantovyh territorij i tuzemcy ih lovyat. Takie
slony gorazdo luchshe svoih sorodichej iz drugih oblastej, i sejchas nam prosto
povezlo, chto my mozhem kupit' zhivotnoe, kotoroe chuvstvuet sebya v kvantovyh
dzhunglyah, kak doma.
Mister Tompkins osmotrel slona so vseh storon. CHto i govorit', eto bylo
ochen' krasivoe, ogromnoe zhivotnoe, odnako, mister Tomtgkins ne zametil v
povadkah slona kakih-libo otlichij po sravneniyu s temi slonami, kotoryh emu
dovodilos' videt' v zooparke.
- Vy govorite, chto eto kvantovyj slon, a dlya menya on vpolne obychnyj
slon i vedet sebya ne tak zanyatno, kak bil'yardnye shary, sdelannye iz bivnej
nekotoryh iz ego sorodichej. Naprimer, pochemu on ne rasplyvaetsya po vsem
napravleniyam? - obratilsya mister Tompkins k professoru.
- Vy medlenno shvatyvaete sut' dela, - zametil professor. - Slon ne
rasplyvaetsya iz-za svoej ochen' bol'shoj massy. Nekotoroe vremya nazad ya uzhe
ob座asnyal vam, chto neopredelennost' v polozhenii i skorosti zavisit ot massy.
CHem bol'she massa, tem men'she neopredelennost'. Imenno poetomu kvantovye
zakony ne nablyudayutsya v obychnom mire dazhe dlya takih legkih tel, kak pylinki,
no stanovyatsya vpolne zametnymi dlya elektronov, kotorye v milliardy
milliardov raz legche pylinok. No v kvantovyh dzhunglyah kvantovaya postoyannaya
gorazdo bol'she, no vse zhe nedostatochno velika, chtoby porozhdat' porazitel'nye
effekty v povedenii stol' tyazhelogo zhivotnogo, kak slon. Neopredelennost' v
polozhenii kvantovogo slona mozhno zametit', tol'ko esli pristal'no vglyadet'sya
v ego ochertaniya. Vozmozhno, vy zametili, chto poverhnost' slonovoj kozhi ne
vpolne opredelenna i kazhetsya neskol'ko neotchetlivo vidimoj. So vremenem eta
neopredelennost' uvelichivaetsya ochen' medlenno. Mne kazhetsya, chto imenno s
etim obstoyatel'stvom svyazana mestnaya legenda, budto u staryh slonov iz
kvantovyh dzhunglej dlinnaya sherst'. YA polagayu, chto na ne stol' krupnyh
zhivotnyh, obitayushchih v kvantovyh dzhunglyah, zamechatel'nye kvantovye effekty
budut bolee zametnymi.
- Horosho, chto v etu ekspediciyu my otpravlyaemsya ne verhom na loshadyah, -
podumal mister Tompkins. - Ved' esli by my vzdumali otpravit'sya v kvantovye
dzhungli na loshadyah, ya nikogda ne mog by skazat' s uverennost'yu, gde moya
loshad' - u menya pod sedlom ili v sleduyushchej doline.
Posle togo, kak professor i ser Richard so svoimi ruzh'yami vzgromozdilis'
v korzinu, ukreplennuyu na spine slona, a mister Tompkins v novoj dlya sebya
dolzhnosti pogonshchika zanyal svoe mesto na shee slona, krepko szhimaya v ruke
nekoe podobie bagra - strekalo, kotorym _nastoyashchie_ pogonshchiki upravlyayut
svoim podopechnym; ekspediciya tronulas' v put' k tainstvennym dzhunglyam.
Ot zhitelej goroda nashi puteshestvenniki uznali, chto dobrat'sya do
dzhunglej mozhno primerno za chas, i mister Tompkins, izo vseh sil pytayas'
sohranit' ravnovesie mezhdu ushami slona, voznamerilsya s pol'zoj ispol'zovat'
vremya, chtoby porassprosit' u professora o kvantovyh yavleniyah.
- Skazhite, pozhalujsta, - nachal mister Tompkins, povernuvshis' k
professoru, - _pochemu_ tela s maloj massoj vedut sebya stol' neobychno i kak
mozhno istolkovat' s tochki zreniya obychnogo zdravogo smysla tu kvantovuyu
postoyannuyu, o kotoroj vy vse vremya govorite?
- O, - voskliknul professor, - ponyat' eto ne tak uzh trudno. Neobychnoe
povedenie vseh ob容ktov v kvantovom mire ob座asnyaetsya prosto tem, chto vy na
nih smotrite.
- Oni nastol'ko stydlivy? - ulybnulsya mister Tompkins.
- "Stydlivy" - ne to slovo, - surovo otvetstvoval professor. - Sut'
dela v tom, chto vsyakij raz, proizvodya lyuboe nablyudenie, vy nepremenno
vozmushchaete dvizhenie nablyudaemogo ob容kta. Raz vy uznaete chto-to o dvizhenii
kakogo-to tela, to eto oznachaet, chto dvizhushcheesya telo proizvelo kakoe-to
dejstvie na vashi organy chuvstv ili na pribor, kotoryj vy ispol'zovali pri
nablyudenii. V silu ravenstva dejstviya i protivodejstviya my prihodim k
zaklyucheniyu, chto vash izmeritel'nyj pribor takzhe vozdejstvoval na telo i, tak
skazat', "isportil" ego dvizhenie, vvedya neopredelennost' v polozhenie i
skorost' tela.
- Esli by ya tronul bil'yardnyj shar pal'cem, to, konechno, vnes by
vozmushchenie v ego dvizhenie, - nedoumenno proiznes mister Tompkins. - No ya
tol'ko posmotrel na nego. Neuzheli etogo dostatochno, chtoby vozmutit' dvizhenie
bil'yardnogo shara?
- Razumeetsya, vpolne dostatochno! Vy zhe ne mozhete videt' bil'yardnyj shar
v kromeshnoj t'me. A esli vy vynesete shar na svet, to luchi sveta,
otrazhayushchiesya ot shara i delayushchie ego vidimym, vozdejstvuyut na nego (my
govorim o takom vozdejstvii kak o "davlenii sveta") i "portyat" dvizhenie
shara.
- A chto esli ya vospol'zuyus' ochen' tonkimi i ochen' chuvstvitel'nymi
priborami? Razve ne smogu ya sdelat' vozdejstvie moih priborov na dvizhushcheesya
telo prenebrezhimo malym?
- Imenno tak my schitali, kogda u nas byla tol'ko klassicheskaya fizika,
do otkrytiya _kvanta dejstviya_. No v nachale XX stoletiya stalo yasno, chto
dejstvie na lyuboj ob容kt ne mozhet byt' nizvedeno do urovnya nizhe
opredelennogo predela, nazyvaemogo kvantovoj postoyannoj i oboznachaemogo
simvolom h. V obychnom mire kvant dejstviya ochen' mal; v obychnyh edinicah on
vyrazhaetsya chislom s dvadcat'yu sem'yu nulyami posle desyatichnoj zapyatoj. Kvant
dejstviya stanovitsya sushchestvennym tol'ko dlya takih legkih chastic, kak
elektrony: iz-za ih ochen' maloj massy na dvizhenii takih chastic zametno
skazyvayutsya i ochen' slabye vozdejstviya. V kvantovyh dzhunglyah, k kotorym my
sejchas priblizhaemsya, kvant dejstviya ochen' velik. |to grubyj mir, v kotorom
delikatnye dejstviya nevozmozhny. Esli kto-nibud' v takom mire popytaetsya
pogladit' kotenka, to tot libo voobshche ne oshchutit nikakoj laski, libo ego sheya
budet slomana pri pervom zhe prikosnovenii.
- Vse eto horosho, - zadumchivo progovoril mister Tompkins, - no vedut li
tela sebya prilichno, t.e. tak, kak obychno prinyato dumat', kogda na nih nikto
ne smotrit?
- Kogda na tela nikto ne smotrit, - otvetil professor, - nikto ne mozhet
skazat', kak oni sebya vedut. Vash vopros ne imeet fizicheskogo smysla.
- Dolzhen priznat'sya, - zametil mister Tompkins, - chto vse eto izryadno
smahivaet na filosofiyu, a ne na fiziku.
- Mozhete nazyvat' eto filosofiej, - professor byl yavno zadet, - no, v
dejstvitel'nosti, rech' idet o fundamental'nom principe sovremennoj fiziki -
_nikogda ne govorit' o tom, chego ne znaesh'_. Vsya sovremennaya fizicheskaya
teoriya osnovana na etom principe, mezhdu tem, kak filosofy obychno upuskayut
ego iz vidu. Naprimer, znamenityj nemeckij filosof Kant provel nemalo
vremeni, razmyshlyaya o svojstvah tel, ne takih, kakimi oni "vidyatsya nam", a
takih, kakie oni est' " v sebe". Dlya sovremennogo fizika imeyut smysl tol'ko
tak nazyvaemye "nablyudaemye" (t. e. principial'no nablyudaemye svojstva), i
vsya sovremennaya fizika osnovana na otnosheniyah mezhdu nablyudaemymi svojstvami.
To, chto nevozmozhno nablyudat', horosho tol'ko dlya prazdnyh razmyshlenij: vy
mozhete pridumyvat' chto ugodno, i plody vashih razmyshlenij nel'zya ni proverit'
(t. e. ubedit'sya v ih sushchestvovanii), ni vospol'zovat'sya imi. Dolzhen
skazat', chto...
 V etot moment uzhasnyj rev potryas vozduh. Slon ostanovilsya kak vkopannyj
tak vnezapno, chto mister Tompkins chut' ne svalilsya. Ogromnaya staya neskol'ko
razmazannyh tigrov napala na slona, vyprygnuv iz zasady so vseh storon. Ser
Richard shvatil svoe ruzh'e i, pricelivshis' blizhajshemu tigru mezhdu glaz,
spustil kurok. V sleduyushchij moment mister Tompkins otchetlivo uslyshal, kak ser
Richard proburchal sebe pod nos nekoe krepkoe vyrazhenie, prinyatoe sredi
ohotnikov. Eshche by! Vystrel byl metkim, no pulya proshla skvoz' golovu tigra,
ne prichiniv tomu ni malejshego vreda!
- Strelyaj eshche! - zakrichal professor. - Ne cel'tes'! Postarajtes'
sozdat' vokrug sebya kak mozhno bol'shuyu plotnost' ognya! Na nas napal tol'ko
odin tigr, no on raspredelen vokrug nashego slona, i nash edinstvennyj shans na
spasenie sostoit v tom, chtoby podnyat' gamil'tonian.
Professor shvatil drugoe ruzh'e, i grohot vystrelov smeshalsya s revom
kvantovogo tigra. Misteru Tompkinsu pokazalos', chto proshla celaya vechnost'
prezhde, chem ves' etot uzhasnyj shum zatih. Odna iz pul' "popala v cel'", i k
velichajshemu udivleniyu mistera Tomtpsinsa tigr, vnezapno prevrativshijsya v
odnogo-edinstvennogo titra, byl s siloj otbroshen nazad, i ego mertvoe telo,
opisav dugu v vozduhe, prizemlilos' gde-to za mayachivshej v otdalenii
pal'movoj roshchej.
- A kto etot Gamil'tonian? - sprosil mister Tompkins, kogda vse nemnogo
uspokoilos'. - Znamenityj ohotnik, kotorogo vy hoteli podnyat' iz mogily,
chtoby on spas nas?
- O, proshu velikodushno prostit' menya! - skazal professor. - V pylu
bitvy ya pereshel na nauchnuyu terminologiyu, kotoruyu vy ne ponimaete!
Gamil'tonianom prinyato nazyvat' matematicheskoe vyrazhenie, opisyvayushchee
kvantovoe vzaimodejstvie mezhdu dvumya telami. Ono poluchilo svoe nazvanie v
chest' irlandskogo matematika Gamil'tona, kotoryj pervym nachal ispol'zovat'
etu matematicheskuyu formu. YA hotel skazat', chto, vypuskaya kak mozhno bol'she
pul', my mozhem uvelichit' veroyatnost' vzaimodejstviya mezhdu pulej i telom
tigra. V kvantovom mire vy ne mozhete tochno pricelit'sya i byt' uvereny, chto
popadete v cel'. Iz-za rasplyvaniya puli i celi vsegda sushchestvuet lish'
otlichnaya ot nulya veroyatnost' popadaniya v cel', no eta veroyatnost' nikogda ne
ravna edinice. V nashem sluchae my vypustili po krajnej mere tridcat' pul',
prezhde chem dejstvitel'no popali v tigra, i togda dejstvie puli okazalos'
stol' sil'nym, chto tigra otbrosilo daleko nazad. To zhe samoe, tol'ko v
men'shih masshtabah, proishodit i v nashem privychnom mire. Kak ya uzhe upominal,
v obychnom mire, chtoby zametit' nechto podobnoe, neobhodimo issledovat'
povedenie takih malyh chastic, kak elektrony. Vozmozhno, vam prihodilos'
slyshat' o tom, chto kazhdyj atom sostoit iz sravnitel'no tyazhelogo yadra i
neskol'kih elektronov, obrashchayushchihsya vokrug nego. Snachala prinyato bylo
dumat', chto dvizhenie elektronov vokrug yadra sovershenno analogichno dvizheniyu
planet vokrug Solnca, no bolee glubokij analiz pokazal, chto obychnye ponyatiya,
otnosyashchiesya k dvizheniyu, slishkom gruby dlya takoj miniatyurnoj sistemy, kak
atom. Dejstviya, igrayushchie vazhnuyu rol' vnutri atoma, po poryadku velichiny
sravnimy s elementarnym kvantom dejstviya, i poetomu vsya kartina v celom
sil'no rasplyvaetsya. Dvizhenie elektrona vokrug atomnogo yadra vo mnogih
otnosheniyah analogichno dvizheniyu nashego kvantovogo tigra, kotoryj v odinochku
okruzhil nashego slona so vseh storon.
- A ne strelyal li kto-nibud' v elektron tak, kak my strelyali v tigra? -
sprosil mister Tompkins.
- Strelyali i ne raz! YAdro samo ispuskaet inogda kvanty sveta vysokoj
energii, ili, chto to zhe, elementarnye porcii dejstviya sveta. V elektron
mozhno vystrelit' i snaruzhi atoma, osveshchaya atom puchkom sveta. Pri etom vse
proizojdet tak zhe, kak s tigrom: mnogie kvanty sveta projdut cherez to mesto,
gde nahoditsya elektron, ne okazav na togo ni malejshego dejstviya, poka,
nakonec, odin iz kvantov sveta ne stolknetsya s elektronom i ne vyb'et ego iz
atoma. Na kvantovuyu sistemu nel'zya vozdejstvovat' chut'-chut'; ona libo voobshche
ne ispytyvaet nikakogo vozdejstviya, libo preterpevaet v rezul'tate
vozdejstviya sil'nye izmeneniya.
- Kak tot neschastnyj kotenok, kotorogo nel'zya prilaskat' v kvantovom
mire, ne riskuya nanesti emu smertel'noe uvech'e, - zaklyuchil mister Tompkins.
- Vzglyanite von tuda! Gazeli! Mnozhestvo gazelej! - voskliknul ser
Richard, podnimaya svoe ruzh'e. I, dejstvitel'no, ogromnoe stado gazelej
pokazalos' iz bambukovoj roshchi.
- Dressirovannye gazeli, - podumal mister Tompkins. - Begut stroem, kak
soldaty na parade. Hotel by ya znat', uzh ne kvantovyj li eto effekt?
V etot moment uzhasnyj rev potryas vozduh. Slon ostanovilsya kak vkopannyj
tak vnezapno, chto mister Tompkins chut' ne svalilsya. Ogromnaya staya neskol'ko
razmazannyh tigrov napala na slona, vyprygnuv iz zasady so vseh storon. Ser
Richard shvatil svoe ruzh'e i, pricelivshis' blizhajshemu tigru mezhdu glaz,
spustil kurok. V sleduyushchij moment mister Tompkins otchetlivo uslyshal, kak ser
Richard proburchal sebe pod nos nekoe krepkoe vyrazhenie, prinyatoe sredi
ohotnikov. Eshche by! Vystrel byl metkim, no pulya proshla skvoz' golovu tigra,
ne prichiniv tomu ni malejshego vreda!
- Strelyaj eshche! - zakrichal professor. - Ne cel'tes'! Postarajtes'
sozdat' vokrug sebya kak mozhno bol'shuyu plotnost' ognya! Na nas napal tol'ko
odin tigr, no on raspredelen vokrug nashego slona, i nash edinstvennyj shans na
spasenie sostoit v tom, chtoby podnyat' gamil'tonian.
Professor shvatil drugoe ruzh'e, i grohot vystrelov smeshalsya s revom
kvantovogo tigra. Misteru Tompkinsu pokazalos', chto proshla celaya vechnost'
prezhde, chem ves' etot uzhasnyj shum zatih. Odna iz pul' "popala v cel'", i k
velichajshemu udivleniyu mistera Tomtpsinsa tigr, vnezapno prevrativshijsya v
odnogo-edinstvennogo titra, byl s siloj otbroshen nazad, i ego mertvoe telo,
opisav dugu v vozduhe, prizemlilos' gde-to za mayachivshej v otdalenii
pal'movoj roshchej.
- A kto etot Gamil'tonian? - sprosil mister Tompkins, kogda vse nemnogo
uspokoilos'. - Znamenityj ohotnik, kotorogo vy hoteli podnyat' iz mogily,
chtoby on spas nas?
- O, proshu velikodushno prostit' menya! - skazal professor. - V pylu
bitvy ya pereshel na nauchnuyu terminologiyu, kotoruyu vy ne ponimaete!
Gamil'tonianom prinyato nazyvat' matematicheskoe vyrazhenie, opisyvayushchee
kvantovoe vzaimodejstvie mezhdu dvumya telami. Ono poluchilo svoe nazvanie v
chest' irlandskogo matematika Gamil'tona, kotoryj pervym nachal ispol'zovat'
etu matematicheskuyu formu. YA hotel skazat', chto, vypuskaya kak mozhno bol'she
pul', my mozhem uvelichit' veroyatnost' vzaimodejstviya mezhdu pulej i telom
tigra. V kvantovom mire vy ne mozhete tochno pricelit'sya i byt' uvereny, chto
popadete v cel'. Iz-za rasplyvaniya puli i celi vsegda sushchestvuet lish'
otlichnaya ot nulya veroyatnost' popadaniya v cel', no eta veroyatnost' nikogda ne
ravna edinice. V nashem sluchae my vypustili po krajnej mere tridcat' pul',
prezhde chem dejstvitel'no popali v tigra, i togda dejstvie puli okazalos'
stol' sil'nym, chto tigra otbrosilo daleko nazad. To zhe samoe, tol'ko v
men'shih masshtabah, proishodit i v nashem privychnom mire. Kak ya uzhe upominal,
v obychnom mire, chtoby zametit' nechto podobnoe, neobhodimo issledovat'
povedenie takih malyh chastic, kak elektrony. Vozmozhno, vam prihodilos'
slyshat' o tom, chto kazhdyj atom sostoit iz sravnitel'no tyazhelogo yadra i
neskol'kih elektronov, obrashchayushchihsya vokrug nego. Snachala prinyato bylo
dumat', chto dvizhenie elektronov vokrug yadra sovershenno analogichno dvizheniyu
planet vokrug Solnca, no bolee glubokij analiz pokazal, chto obychnye ponyatiya,
otnosyashchiesya k dvizheniyu, slishkom gruby dlya takoj miniatyurnoj sistemy, kak
atom. Dejstviya, igrayushchie vazhnuyu rol' vnutri atoma, po poryadku velichiny
sravnimy s elementarnym kvantom dejstviya, i poetomu vsya kartina v celom
sil'no rasplyvaetsya. Dvizhenie elektrona vokrug atomnogo yadra vo mnogih
otnosheniyah analogichno dvizheniyu nashego kvantovogo tigra, kotoryj v odinochku
okruzhil nashego slona so vseh storon.
- A ne strelyal li kto-nibud' v elektron tak, kak my strelyali v tigra? -
sprosil mister Tompkins.
- Strelyali i ne raz! YAdro samo ispuskaet inogda kvanty sveta vysokoj
energii, ili, chto to zhe, elementarnye porcii dejstviya sveta. V elektron
mozhno vystrelit' i snaruzhi atoma, osveshchaya atom puchkom sveta. Pri etom vse
proizojdet tak zhe, kak s tigrom: mnogie kvanty sveta projdut cherez to mesto,
gde nahoditsya elektron, ne okazav na togo ni malejshego dejstviya, poka,
nakonec, odin iz kvantov sveta ne stolknetsya s elektronom i ne vyb'et ego iz
atoma. Na kvantovuyu sistemu nel'zya vozdejstvovat' chut'-chut'; ona libo voobshche
ne ispytyvaet nikakogo vozdejstviya, libo preterpevaet v rezul'tate
vozdejstviya sil'nye izmeneniya.
- Kak tot neschastnyj kotenok, kotorogo nel'zya prilaskat' v kvantovom
mire, ne riskuya nanesti emu smertel'noe uvech'e, - zaklyuchil mister Tompkins.
- Vzglyanite von tuda! Gazeli! Mnozhestvo gazelej! - voskliknul ser
Richard, podnimaya svoe ruzh'e. I, dejstvitel'no, ogromnoe stado gazelej
pokazalos' iz bambukovoj roshchi.
- Dressirovannye gazeli, - podumal mister Tompkins. - Begut stroem, kak
soldaty na parade. Hotel by ya znat', uzh ne kvantovyj li eto effekt?
 Gruppa gazelej bystro priblizhalas' k slonu, na kotorom vossedali nashi
puteshestvenniki, i ser Richard izgotovilsya bylo strelyat', kak vdrug professor
ostanovil ego.
- Ne trat'te ponaprasnu vashi ohotnich'i pripasy, - skazal professor. -
Ochen' malo shansov popast' v zhivotnoe, kogda ono dvizhetsya v difrakcionnoj
kartine.
- Pochemu vy govorite ne o zhivotnyh, a ob odnom zhivotnom, udivlenno
sprosil ser Richard. - Zdes' po krajnej mere neskol'ko dyuzhin gazelej!
- Vy gluboko zabluzhdaetes', - vozrazil professor. - Zdes' pered nami
tol'ko odna malen'kaya gazel', kotoraya, ispugavshis' chego-to, mchitsya skvoz'
bambukovuyu roshchu. Delo v tom, chto "rasplyvanie" vseh tel obladaet odnim
svojstvom, analogichnym svojstvu obychnogo sveta: prohodya cherez pravil'nuyu
sistemu otverstij ("reshetku"), naprimer mezhdu stvolami bambuka v roshche, ono
porozhdaet yavlenie difrakcii, o kotorom vam, veroyatno, prihodilos' slyshat' v
shkole. Poetomu my govorim o volnovom haraktere materii.
No ni ser Richard, ni mister Tompkins ne mogli vspomnit', chto zhe,
sobstvenno govorya, oznachaet zagadochnoe slovo "difrakciya" i razgovor
oborvalsya.
Uglubivshis' v debri kvantovyh dzhunglej, nashi puteshestvenniki
povstrechali mnozhestvo drugih interesnejshih yavlenij, naprimer, poznakomilis'
s kvantovymi moskitami. Opredelit' mestonahozhdenie etih nasekomyh v
prostranstve bylo pochti nevozmozhno iz-za ih maloj massy. Ochen' zabavny byli
kvantovye obez'yany.
No vot vperedi pokazalos' chto-to napominayushchee tuzemnoe selenie.
- YA ne znal, chto v etih mestah zhivut lyudi, - zametil professor. - Sudya
po shumu, u nih kakoe-to prazdnestvo. Vy tol'ko prislushajtes' k neumolkaemomu
zvonu kolokol'chikov.
Razlichit' otdel'nye figury tuzemcev, ispolnyavshih vokrug bol'shogo kostra
kakoj-to dikij tanec, bylo ochen' trudno. Iz tolpy, kuda ni glyan', vsyudu
podnimalis' temno-korichnevye ruki s kolokol'chikami vseh razmerov. Kogda
puteshestvenniki priblizilis', vse, vklyuchaya hizhiny i okruzhavshie selenie
bol'shie derev'ya, nachalo rasplyvat'sya. Zvon kolokol'chikov stal nevynosimym
dlya mistera Tompkinsa. On protyanul ruku, shvatil chto-to i otbrosil v
storonu. Budil'nik razbil stakan s vodoj, stoyavshij na nochnom stolike, i
potok holodnoj vody privel mistera Tompkinsa v chuvstvo. On vskochil i
prinyalsya bystro odevat'sya. CHerez polchasa emu nuzhno bylo byt' v banke.
Glava 9
Demon Maksvella
Uchastvuya na protyazhenii mnogih mesyacev v neveroyatnyh priklyucheniyah, v
hode kotoryh professor ne upuskal udobnogo sluchaya posvyatit' mistera
Tompkinsa v tajny fiziki, mister Tompkins vse bolee pronikalsya ocharovaniem
miss Mod. Nakonec, nastal den', kogda mister Tompkins, zaikayas' i krasneya ot
smushcheniya, robko predlozhil miss Mod ruku i serdce. Predlozhenie bylo s
radost'yu prinyato, i vskore mister Tompkins i miss Mod stali muzhem i zhenoj. V
novoj dlya sebya roli testya professor schital svoej nepremennoj obyazannost'yu
vsyacheski sposobstvovat' rasshireniyu poznanij svoego zyatya v fizike i znakomit'
ego s novejshimi dostizheniyami etoj uvlekatel'noj nauki.
Odnazhdy mister i missis Tompkins, s udobstvom ustroivshis' v kreslah,
predavalis' voskresnomu otdyhu v svoej uyutnoj kvartirke. Missis Tompkins s
golovoj pogruzilas' v izuchenie zhurnala mod "Vogue", a ee suprug s uvlecheniem
chital stat'yu v zhurnale "Esquire" {Esli byt' tochnym, to sleduet skazat', chto
vnimanie mistera Tompkinsa privlekla stat'ya v yanvarskom nomere etogo zhurnala
za 1940 g.}.
- Podumat' tol'ko! - vnezapno voskliknul mister Tompkins. -
Okazyvaetsya, v azartnyh igrah sushchestvuyut besproigryshnye strategii!
- Siril, neuzheli ty vser'ez dumaesh', chto takoe vozmozhno? - sprosila
missis Tompkins, zadumchivo podnimaya glaza ot prikovavshih ee vnimanie stranic
modnogo zhurnala. - Pomnitsya, papa ne raz govoril nam o tom, chto v azartnyh
igrah besproigryshnyh strategij net i byt' i ne mozhet.
Gruppa gazelej bystro priblizhalas' k slonu, na kotorom vossedali nashi
puteshestvenniki, i ser Richard izgotovilsya bylo strelyat', kak vdrug professor
ostanovil ego.
- Ne trat'te ponaprasnu vashi ohotnich'i pripasy, - skazal professor. -
Ochen' malo shansov popast' v zhivotnoe, kogda ono dvizhetsya v difrakcionnoj
kartine.
- Pochemu vy govorite ne o zhivotnyh, a ob odnom zhivotnom, udivlenno
sprosil ser Richard. - Zdes' po krajnej mere neskol'ko dyuzhin gazelej!
- Vy gluboko zabluzhdaetes', - vozrazil professor. - Zdes' pered nami
tol'ko odna malen'kaya gazel', kotoraya, ispugavshis' chego-to, mchitsya skvoz'
bambukovuyu roshchu. Delo v tom, chto "rasplyvanie" vseh tel obladaet odnim
svojstvom, analogichnym svojstvu obychnogo sveta: prohodya cherez pravil'nuyu
sistemu otverstij ("reshetku"), naprimer mezhdu stvolami bambuka v roshche, ono
porozhdaet yavlenie difrakcii, o kotorom vam, veroyatno, prihodilos' slyshat' v
shkole. Poetomu my govorim o volnovom haraktere materii.
No ni ser Richard, ni mister Tompkins ne mogli vspomnit', chto zhe,
sobstvenno govorya, oznachaet zagadochnoe slovo "difrakciya" i razgovor
oborvalsya.
Uglubivshis' v debri kvantovyh dzhunglej, nashi puteshestvenniki
povstrechali mnozhestvo drugih interesnejshih yavlenij, naprimer, poznakomilis'
s kvantovymi moskitami. Opredelit' mestonahozhdenie etih nasekomyh v
prostranstve bylo pochti nevozmozhno iz-za ih maloj massy. Ochen' zabavny byli
kvantovye obez'yany.
No vot vperedi pokazalos' chto-to napominayushchee tuzemnoe selenie.
- YA ne znal, chto v etih mestah zhivut lyudi, - zametil professor. - Sudya
po shumu, u nih kakoe-to prazdnestvo. Vy tol'ko prislushajtes' k neumolkaemomu
zvonu kolokol'chikov.
Razlichit' otdel'nye figury tuzemcev, ispolnyavshih vokrug bol'shogo kostra
kakoj-to dikij tanec, bylo ochen' trudno. Iz tolpy, kuda ni glyan', vsyudu
podnimalis' temno-korichnevye ruki s kolokol'chikami vseh razmerov. Kogda
puteshestvenniki priblizilis', vse, vklyuchaya hizhiny i okruzhavshie selenie
bol'shie derev'ya, nachalo rasplyvat'sya. Zvon kolokol'chikov stal nevynosimym
dlya mistera Tompkinsa. On protyanul ruku, shvatil chto-to i otbrosil v
storonu. Budil'nik razbil stakan s vodoj, stoyavshij na nochnom stolike, i
potok holodnoj vody privel mistera Tompkinsa v chuvstvo. On vskochil i
prinyalsya bystro odevat'sya. CHerez polchasa emu nuzhno bylo byt' v banke.
Glava 9
Demon Maksvella
Uchastvuya na protyazhenii mnogih mesyacev v neveroyatnyh priklyucheniyah, v
hode kotoryh professor ne upuskal udobnogo sluchaya posvyatit' mistera
Tompkinsa v tajny fiziki, mister Tompkins vse bolee pronikalsya ocharovaniem
miss Mod. Nakonec, nastal den', kogda mister Tompkins, zaikayas' i krasneya ot
smushcheniya, robko predlozhil miss Mod ruku i serdce. Predlozhenie bylo s
radost'yu prinyato, i vskore mister Tompkins i miss Mod stali muzhem i zhenoj. V
novoj dlya sebya roli testya professor schital svoej nepremennoj obyazannost'yu
vsyacheski sposobstvovat' rasshireniyu poznanij svoego zyatya v fizike i znakomit'
ego s novejshimi dostizheniyami etoj uvlekatel'noj nauki.
Odnazhdy mister i missis Tompkins, s udobstvom ustroivshis' v kreslah,
predavalis' voskresnomu otdyhu v svoej uyutnoj kvartirke. Missis Tompkins s
golovoj pogruzilas' v izuchenie zhurnala mod "Vogue", a ee suprug s uvlecheniem
chital stat'yu v zhurnale "Esquire" {Esli byt' tochnym, to sleduet skazat', chto
vnimanie mistera Tompkinsa privlekla stat'ya v yanvarskom nomere etogo zhurnala
za 1940 g.}.
- Podumat' tol'ko! - vnezapno voskliknul mister Tompkins. -
Okazyvaetsya, v azartnyh igrah sushchestvuyut besproigryshnye strategii!
- Siril, neuzheli ty vser'ez dumaesh', chto takoe vozmozhno? - sprosila
missis Tompkins, zadumchivo podnimaya glaza ot prikovavshih ee vnimanie stranic
modnogo zhurnala. - Pomnitsya, papa ne raz govoril nam o tom, chto v azartnyh
igrah besproigryshnyh strategij net i byt' i ne mozhet.
 - Vzglyani sama, Mod, - predlozhil mister Tompkins, pokazyvaya svoej
supruge stat'yu, kotoruyu on izuchal s takim interesom v techenie poslednego
poluchasa. - YA nichego ne znayu o drugih vyigryshnyh strategiyah, no ta, o
kotoroj govoritsya v etoj stat'e, osnovana na ochen' prostyh matematicheskih
raschetah bez vsyakih obmanov i podvohov, i ya prosto ne znayu, gde zdes' v
rassuzhdeniya mozhet vkrast'sya kakaya-nibud' oshibka. CHtoby vyigrat', nuzhno lish'
vypisat' na listke bumagi chisla
�1, 2, 3 �
i neukosnitel'no priderzhivat'sya prostyh pravil, privodimyh v toj zhe stat'e.
- Poprobovat', konechno, mozhno, - soglasilas' Mod, nachinaya proyavlyat'
priznaki interesa. - A chto eto za pravila?
- Dlya bol'shej naglyadnosti ya budu sledovat' primeru, privodimomu v
stat'e, ved', kak ty znaesh', uchit'sya luchshe vsego na primerah. V kachestve
illyustracii besproigryshnoj strategii avtor stat'i vybral igru v ruletku. Kak
tebe, dolzhno byt', izvestno, igroki v ruletku delayut stavku na krasnoe ili
na chernoe, t. e., po sushchestvu, kak by zaklyuchayut mezhdu soboj pari
otnositel'no ishoda brosaniya monety - vypadet li moneta vverh orlom ili
reshkoj. YA nachinayu s togo, chto vypisyvayu na listke bumagi chisla
�1, 2, 3. �
Pervoe pravilo sostoit v tom, chto, delaya stavku, ya dolzhen vylozhit' na
stol chislo fishek, ravnoe summe pervogo i poslednego i vypisannyh chisel (a v
tom sluchae, esli na listke bumagi ostanetsya odno-edinstvennoe chislo, stavka
dolzhna byt' ravna odnomu chislu). Sleduya etomu pravilu, ya dolzhen vylozhit' na
stol chetyre (odnu plyus tri) fishki. Predpolozhim, chto ya stavlyu na krasnoe. Po
pravilam igry, v sluchae vyigrysha mne nuzhno zacherknut' pervoe i poslednee iz
vypisannyh chisel. V nashem primere eto chisla 1 i 3, poetomu, delaya sleduyushchuyu
stavku, ya dolzhen vylozhit' na stol dve fishki (poskol'ku posle vycherkivaniya
chisel 1 i 3 na listke bumagi ostanetsya odno-edinstvennoe chislo 2). V sluchae
proigrysha chislo fishek v predydushchej (proigrannoj) stavke neobhodimo pripisat'
sprava k uzhe vypisannym chislam, a pri opredelenii velichiny sleduyushchej stavki
priderzhivat'sya prezhnego pravila, t. e. vystavit' chislo fishek, ravnoe summe
pervogo i poslednego iz vypisannyh chisel (libo, esli na listke bumagi
ostanetsya tol'ko odno chislo, to etomu chislu).
Predpolozhim, chto ruletka ostanovitsya na chernom i krup'e special'noj
lopatkoj podvinet k sebe vystavlennye mnoj chetyre fishki. Poskol'ku ya
proigral, novyj ryad chisel, vypisannyh na listke bumagi, vyglyadit teper' tak:
�1, 2, 3, 4 �
(chislo vylozhennyh na stol fishek, ravnoe 4, pripisano sprava). Delaya
sleduyushchuyu stavku, ya dolzhen vylozhit' na stol pyat' (odnu plyus chetyre) fishek. V
stat'e govoritsya, chto i vo vtoroj raz ya snova proigryvayu i chto, nesmotrya na
povtornyj proigrysh, mne nadlezhit priderzhivat'sya prezhnej strategii, t. e.
pripisat' k uzhe vypisannym chislam sprava chislo 5 i vylozhit' na stol shest'
(odnu plyus pyat') fishek.
- Na etot raz ty nepremenno dolzhen vyigrat', - voskliknula Mod, vse
bolee vhodya v azart. - Ne mozhesh' zhe ty vse vremya proigryvat'!
- Eshche kak mogu! - zaveril suprugu mister Tompkins. - V detstve ya
chasten'ko igral s drugimi mal'chishkami v orlyanku - zaklyuchal pari otnositel'no
togo, kakoj storonoj vverh vypadet broshennaya moneta i, hochesh' ver', hochesh'
ne ver', odnazhdy stal svidetelem togo, kak moneta desyat' raz podryad vypala
vverh orlom. No predpolozhim, kak eto delaetsya v stat'e, chto na etot raz ya
dlya raznoobraziya vyigral. V etom sluchae po pravilam igry ya dolzhen poluchit'
svoyu udvoennuyu stavku - dvenadcat' fishek - i po sravneniyu so svoim
pervonachal'nym kapitalom stanu na tri fishki bogache. Sleduya rekomenduemoj
strategii, ya dolzhen vycherknut' chisla 1 i 5, posle chego zapis' na listke
bumagi primet sleduyushchij vid:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto)
Delaya sleduyushchuyu stavku, ya dolzhen vylozhit' na stol shest' (dve plyus
chetyre) fishek.
- Zdes' v stat'e napisano, chto ty snova proigral, - vzdohnula Mod,
zaglyadyvaya v zhurnal cherez plecho muzha. - Znachit, teper' ty dolzhen pripisat' k
chislam sprava shesterku i, delaya sleduyushchuyu stavku, vylozhit' na stol vosem'
fishek. Pravil'no?
- Ty absolyutno prava, no i na etot raz menya podsteregaet proigrysh, i
zapis' na listke bumagi vyglyadit teper' tak:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto), 6, 8
Delaya ocherednuyu stavku, ya dolzhen teper' vylozhit' na stol desyat' (dve
plyus vosem') fishek. V stat'e govoritsya, chto na etot raz ya vyigral. Znachit, ya
dolzhen zacherknut' chisla 2 i 8 i, delaya sleduyushchuyu stavku, vylozhit' na stol
devyat' (tri plyus shest') fishek. No tut menya (tak govoritsya v stat'e) snova
podsteregaet proigrysh.
- Kakoj vse-taki neudachnyj primer! - posetovala, naduv gubki, Mod. - Ty
uspel proigrat' tri raza, a vyigral vsego lish' odin raz!
- Nevazhno, - uspokoil ee mister Tompkins so snishoditel'noj
uverennost'yu fokusnika. - Vse ravno v samom konce cikla vyigrysh ostanetsya za
nami. Poslednij zapusk ruletki prines mne (po utverzhdeniyu avtora stat'i)
proigrysh v devyat' fishek. Poetomu teper' ya dolzhen pripisat' k uzhe vypisannym
chislam sprava devyatku, posle chego zapis' na moem listke budet vyglyadet' tak:
1 (zacherknuto), 2 (zacherknuto), 3, 4, 5 (zacherknuto), 6, 8 (zacherknuto), 9
Na stol mne nuzhno vylozhit' dvenadcat' (tri plyus devyat') fishek. Na etot
raz vyigrysh ostaetsya za mnoj, poetomu ya vycherkivayu chisla 3 i 9 i, delaya
novuyu stavku, vykladyvayu na stol desyat' (chetyre plyus shest') fishek.
Posleduyushchij vyigrysh zavershaet cikl, tak kak vse chisla, vypisannye na listke
bumagi, okazyvayutsya zacherknutymi. YA stal bogache na shest' fishek, hotya vyigral
v ruletku tol'ko chetyre raza, a proigral pyat' raz!
- A ty dejstvitel'no stal na shest' fishek bogache? - nedoverchivo sprosila
Mod.
- V etom ne mozhet byt' nikakih somnenij. Strategiya postroena tak, chto
vsyakij raz po zavershenii cikla ty, hochesh', ne hochesh', nepremenno vyigryvaesh'
shest' fishek. V etom netrudno ubedit'sya s pomoshch'yu neslozhnyh vychislenij,
poetomu ya nazyvayu etu strategiyu matematicheskoj. Kak vidish', ona
besproigryshna. Esli ugodno, mozhesh' vzyat' listok bumagi i proverit' vse
vykladki sama.
- Veryu tebe na slovo, chto strategiya dejstvitel'no besproigryshna, -
zadumchivo skazala Mod, - no ved' shest' fishchek - ne takoj uzh bol'shoj vyigrysh.
- Kak skazat', - vozrazil mister Tompkins, - ved' vyigrysh shesti fishek v
konce kazhdogo cikla _garantirovan_. Povtoryaya proceduru snova i snova
(nachinaya kazhdyj raz s vypisyvaniya chisel 1, 2, 3), ty mozhesh' vyigrat' skol'ko
tvoej dushe ugodno deneg, a eto sovsem neploho.
- |to prosto velikolepno! - soglasilas' Mod. - Teper' ty smozhesh'
ostavit' sluzhbu v banke, my smozhem pereehat' v bolee prostornuyu kvartiru, a
ne dalee, kak vchera, ya videla v vitrine odnogo mehovogo magazina chudesnoe
manto. I stoit ono kakih-nibud'...
- Razumeetsya, my kupim tebe eto manto, dorogaya, - pospeshil zaverit'
zhenu mister Tompkins. - No snachala nam nuzhno kak mozhno skoree otpravit'sya v
Monte-Karlo. Ved' stat'yu, opublikovannuyu v zhurnale "Esquire", prochitaet
mnozhestvo lyudej, i bylo by ochen' dosadno pribyt' v Monte-Karlo lish' dlya
togo, chtoby zastat' tam schastlivchika, kotoryj operedil nas i dovel kazino do
polnogo razoreniya.
- YA sejchas pozvonyu v aeroport, - predlozhila Mod, - i uznayu, kogda
otpravlyaetsya blizhajshij rejs v Monte-Karlo.
- CHto za speshka? - razdalsya v prihozhej znakomyj golos, i v komnatu
voshel staryj professor. Ostanovivshis' v dveryah, on s udivleniem smotrel na
supruzheskuyu chetu Tompkinsov, neskol'ko razgoryachennyh vnezapno otkryvshimisya
pered nimi perspektivami finansovogo blagopoluchiya.
- My namerevaemsya otpravit'sya blizhajshim zhe rejsom v Monte-Karlo i
nadeemsya vernut'sya osnovatel'no razbogatevshimi, - poyasnil mister Tompkins,
podnimayas' iz kresla navstrechu testyu.
- Ah, vot v chem delo! Togda vse ponyatno, - ulybnulsya professor, s
komfortom ustraivayas' v staromodnom kresle u kamina. - U vas est' novaya
besproigryshnaya strategiya?
- No, papa, eta strategiya dejstvitel'no besproigryshnaya, - s uprekom
skazala Mod, vse eshche derzha ruku na telefonnoj trubke.
- Mod sovershenno prava, - podtverdil mister Tompkins, protyagivaya
professoru zhurnal. - Predlagaemaya strategiya prosto ne mozhet ne vyigrat'!
- Tak-taki i ne mozhet? - ironicheski peresprosil professor s ulybkoj. -
Sejchas uvidim!
Beglo oznakomivshis' so stat'ej, professor prodolzhal:
- Otlichitel'naya osobennost' predlagaemoj strategii sostoit v tom, chto
pravilo, reguliruyushchee velichinu stavok, zastavlyaet vas uvelichivat' stavku
posle kazhdogo proigrysha i snizhat' stavku posle kazhdogo vyigrysha.
Sledovatel'no, esli vy budete poperemenno vyigryvat' i proigryvat', prichem
vyigryshi i proigryshi budut cheredovat'sya s absolyutnoj regulyarnost'yu, to vash
kapital budet kolebat'sya, prichem kazhdoe uvelichenie kapitala budet chut'
bol'she ego umen'sheniya. V etom sluchae vy, nesomnenno, dostatochno skoro
stanete millionerom. No, kak vy ponimaete, absolyutnaya regulyarnost'
vstrechaetsya nechasto. V dejstvitel'nosti veroyatnost' poyavleniya pravil'no
chereduyushchejsya posledovatel'nosti vyigryshej i proigryshej stol' zhe mala, kak i
veroyatnost' poyavleniya odinakovoj po dline serii odnih tol'ko vyigryshej.
Takim obrazom, neobhodimo vyyasnit', chto proizojdet, esli neskol'ko vyigryshej
(ili neskol'ko proigryshej) sleduyut podryad drug za drugom. Esli vam, kak
govoryat igroki, ulybnulas' fortuna, to pravila besproigryshnoj strategii
vynuzhdayut vas libo ponizhat', libo po krajnej mere ne povyshat' stavku posle
kazhdogo vyigrysha, poetomu obshchij vyigrysh okazhetsya ne slishkom bol'shim. S
drugoj storony, te zhe pravila zastavlyayut vas posle kazhdogo proigrysha
povyshat' stavku, poetomu polosa neudach mozhet imet' dlya vas katastroficheskie
posledstviya i dazhe pobudit' vas vyjti iz igry. Krivaya kolebanij vashego
kapitala na etot raz sostoit iz neskol'kih medlenno vozrastayushchih uchastkov,
smenyayushchihsya rezkimi spadami. V nachale igry vy s bol'shej veroyatnost'yu
popadaete na dlinnuyu medlenno vozrastayushchuyu chast' krivoj i v techenie
kakogo-to vremeni naslazhdaetes' priyatnym oshchushcheniem togo, chto vash kapital
medlenno, no neuklonno uvelichivaetsya. No esli vy prodolzhaete igru dostatochno
dolgo v nadezhde na poluchenie vse bol'shej i bol'shej pribyli, to sovershenno
neozhidanno dlya vas vnezapno nastupaet rezkij spad, kotoryj mozhet okazat'sya
dostatochno glubokim dlya togo, chtoby vy, sdelav ocherednuyu stavku, poteryali
poslednij penni. Mozhno pokazat', prichem v sovershenno obshchem vide, chto v
predlagaemoj avtorom stat'i strategii, ravno kak i v lyuboj drugoj vyigryshnoj
strategii, veroyatnost' togo, chto krivaya dostignet dvojnoj otmetki, ravna
veroyatnosti dostignut' nulevogo znacheniya. Inache govorya, vy imeete tochno
takoj zhe shans na okonchatel'nyj vyigrysh, kak esli by postavili vse svoi
den'gi na krasnoe ili chernoe i udvoili svoj kapital ili spustili vse, chto
imeli, za odin-edinstvennyj zapusk ruletki. Vse "besproigryshnye" strategii
sposobny lish' prodlit' igru i tem samym dat' vam vozmozhnost' poluchit' za
svoi den'gi bol'she udovol'stviya. No dazhe esli vy ne trebuete ot igry nichego
bol'shego, to i togda igru ne sleduet tak uslozhnyat'. Kak vy znaete, na obode
kolesa ruletki naneseny tridcat' shest' chisel. Nichto ne meshaet postavit' po
fishke na kazhdoe iz chisel, krome kakogo-nibud' odnogo. V etom sluchae vy
imeete tridcat' pyat' shansov iz tridcati shesti na vyigrysh i na to, chto bank
vyplatit vam za odnu fishku bol'she, chem te tridcat' pyat' fishek, kotorye vy,
delaya stavku, vylozhili na stol. Odnako v odnom iz tridcati shesti zapuskov
ruletochnogo kolesa sharik ostanovitsya na tom chisle, na kotoroe vy reshili ne
stavit' svoyu fishku, i vy poteryaete vse svoi tridcat' pyat' fishek. Esli vy
budete priderzhivat'sya takoj strategii v dostatochno prodolzhitel'noj igre, to
krivaya vashego fluktuiruyushchego kapitala budet vyglyadet' tochno tak zhe, kak
krivaya, kotoruyu vy poluchili, sleduya strategii, predlozhennoj zhurnalom.
Razumeetsya, v svoih rassuzhdeniyah ya ishodil iz predpolozheniya o tom, chto
bank ne predprinimaet nikakih mer, chtoby iskusstvenno ponizit' shansy igroka
na vyigrysh. V dejstvitel'nosti zhe na kazhdom ruletochnom kolese, kotoroe mne
prihodilos' videt', byl nul' - "zero", a inogda dazhe dva nulya, chto ponizhaet
shansy igroka na vyigrysh. Takim obrazom, nezavisimo ot vybrannoj igrokom
strategii ego denezhki malo-pomalu perekochevyvayut iz ego karmana v karman
vladel'ca kazino.
- Vy hotite skazat', - udruchenno progovoril mister Tompkins, - chto
nadezhnoj besproigryshnoj strategii ne sushchestvuet i chto vyigrat' den'gi bez
riska proigrat' s veroyatnost'yu chut' bol'she, chem veroyatnost' vyigrysha, prosto
nevozmozhno?
- Imenno eto ya hotel skazat'! - podtverdil dogadku mistera Tompkinsa
professor. - Bolee togo, vyskazannye mnoj soobrazheniya otnosyatsya ne tol'ko k
takim v sushchnosti pustyakovym problemam, kak azartnye igry, no i ko mnogim
razlichnym fizicheskim yavleniyam, kotorye, na pervyj vzglyad, ne imeyut nikakogo
otnosheniya k veroyatnostnym zakonam. Poetomu esli by vam udalos' izobresti
nadezhnuyu vyigryshnuyu strategiyu dlya preodoleniya zakonov sluchaya, to dlya nee
nashlos' by nemalo gorazdo bolee uvlekatel'nyh primenenij, chem igra na den'gi
v kazino. Naprimer, takaya strategiya pozvolila by sozdavat' avtomashiny,
sposobnye sovershat' probegi lyuboj protyazhennosti bez kapli benzina, stroit'
fabriki, rabotayushchie bez uglya, i osushchestvlyat' mnozhestvo drugih ne menee
fantasticheskih proektov.
- YA gde-to chital o takih fantasticheskih mashinah. Kazhetsya, oni
nazyvayutsya vechnymi dvigatelyami? - zametil mister Tompkins. - Esli ya
pravil'no pomnyu, vechnye dvigateli po zamyslu ih sozdatelej d
- Vzglyani sama, Mod, - predlozhil mister Tompkins, pokazyvaya svoej
supruge stat'yu, kotoruyu on izuchal s takim interesom v techenie poslednego
poluchasa. - YA nichego ne znayu o drugih vyigryshnyh strategiyah, no ta, o
kotoroj govoritsya v etoj stat'e, osnovana na ochen' prostyh matematicheskih
raschetah bez vsyakih obmanov i podvohov, i ya prosto ne znayu, gde zdes' v
rassuzhdeniya mozhet vkrast'sya kakaya-nibud' oshibka. CHtoby vyigrat', nuzhno lish'
vypisat' na listke bumagi chisla
�1, 2, 3 �
i neukosnitel'no priderzhivat'sya prostyh pravil, privodimyh v toj zhe stat'e.
- Poprobovat', konechno, mozhno, - soglasilas' Mod, nachinaya proyavlyat'
priznaki interesa. - A chto eto za pravila?
- Dlya bol'shej naglyadnosti ya budu sledovat' primeru, privodimomu v
stat'e, ved', kak ty znaesh', uchit'sya luchshe vsego na primerah. V kachestve
illyustracii besproigryshnoj strategii avtor stat'i vybral igru v ruletku. Kak
tebe, dolzhno byt', izvestno, igroki v ruletku delayut stavku na krasnoe ili
na chernoe, t. e., po sushchestvu, kak by zaklyuchayut mezhdu soboj pari
otnositel'no ishoda brosaniya monety - vypadet li moneta vverh orlom ili
reshkoj. YA nachinayu s togo, chto vypisyvayu na listke bumagi chisla
�1, 2, 3. �
Pervoe pravilo sostoit v tom, chto, delaya stavku, ya dolzhen vylozhit' na
stol chislo fishek, ravnoe summe pervogo i poslednego i vypisannyh chisel (a v
tom sluchae, esli na listke bumagi ostanetsya odno-edinstvennoe chislo, stavka
dolzhna byt' ravna odnomu chislu). Sleduya etomu pravilu, ya dolzhen vylozhit' na
stol chetyre (odnu plyus tri) fishki. Predpolozhim, chto ya stavlyu na krasnoe. Po
pravilam igry, v sluchae vyigrysha mne nuzhno zacherknut' pervoe i poslednee iz
vypisannyh chisel. V nashem primere eto chisla 1 i 3, poetomu, delaya sleduyushchuyu
stavku, ya dolzhen vylozhit' na stol dve fishki (poskol'ku posle vycherkivaniya
chisel 1 i 3 na listke bumagi ostanetsya odno-edinstvennoe chislo 2). V sluchae
proigrysha chislo fishek v predydushchej (proigrannoj) stavke neobhodimo pripisat'
sprava k uzhe vypisannym chislam, a pri opredelenii velichiny sleduyushchej stavki
priderzhivat'sya prezhnego pravila, t. e. vystavit' chislo fishek, ravnoe summe
pervogo i poslednego iz vypisannyh chisel (libo, esli na listke bumagi
ostanetsya tol'ko odno chislo, to etomu chislu).
Predpolozhim, chto ruletka ostanovitsya na chernom i krup'e special'noj
lopatkoj podvinet k sebe vystavlennye mnoj chetyre fishki. Poskol'ku ya
proigral, novyj ryad chisel, vypisannyh na listke bumagi, vyglyadit teper' tak:
�1, 2, 3, 4 �
(chislo vylozhennyh na stol fishek, ravnoe 4, pripisano sprava). Delaya
sleduyushchuyu stavku, ya dolzhen vylozhit' na stol pyat' (odnu plyus chetyre) fishek. V
stat'e govoritsya, chto i vo vtoroj raz ya snova proigryvayu i chto, nesmotrya na
povtornyj proigrysh, mne nadlezhit priderzhivat'sya prezhnej strategii, t. e.
pripisat' k uzhe vypisannym chislam sprava chislo 5 i vylozhit' na stol shest'
(odnu plyus pyat') fishek.
- Na etot raz ty nepremenno dolzhen vyigrat', - voskliknula Mod, vse
bolee vhodya v azart. - Ne mozhesh' zhe ty vse vremya proigryvat'!
- Eshche kak mogu! - zaveril suprugu mister Tompkins. - V detstve ya
chasten'ko igral s drugimi mal'chishkami v orlyanku - zaklyuchal pari otnositel'no
togo, kakoj storonoj vverh vypadet broshennaya moneta i, hochesh' ver', hochesh'
ne ver', odnazhdy stal svidetelem togo, kak moneta desyat' raz podryad vypala
vverh orlom. No predpolozhim, kak eto delaetsya v stat'e, chto na etot raz ya
dlya raznoobraziya vyigral. V etom sluchae po pravilam igry ya dolzhen poluchit'
svoyu udvoennuyu stavku - dvenadcat' fishek - i po sravneniyu so svoim
pervonachal'nym kapitalom stanu na tri fishki bogache. Sleduya rekomenduemoj
strategii, ya dolzhen vycherknut' chisla 1 i 5, posle chego zapis' na listke
bumagi primet sleduyushchij vid:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto)
Delaya sleduyushchuyu stavku, ya dolzhen vylozhit' na stol shest' (dve plyus
chetyre) fishek.
- Zdes' v stat'e napisano, chto ty snova proigral, - vzdohnula Mod,
zaglyadyvaya v zhurnal cherez plecho muzha. - Znachit, teper' ty dolzhen pripisat' k
chislam sprava shesterku i, delaya sleduyushchuyu stavku, vylozhit' na stol vosem'
fishek. Pravil'no?
- Ty absolyutno prava, no i na etot raz menya podsteregaet proigrysh, i
zapis' na listke bumagi vyglyadit teper' tak:
1 (zacherknuto), 2, 3, 4, 5 (zacherknuto), 6, 8
Delaya ocherednuyu stavku, ya dolzhen teper' vylozhit' na stol desyat' (dve
plyus vosem') fishek. V stat'e govoritsya, chto na etot raz ya vyigral. Znachit, ya
dolzhen zacherknut' chisla 2 i 8 i, delaya sleduyushchuyu stavku, vylozhit' na stol
devyat' (tri plyus shest') fishek. No tut menya (tak govoritsya v stat'e) snova
podsteregaet proigrysh.
- Kakoj vse-taki neudachnyj primer! - posetovala, naduv gubki, Mod. - Ty
uspel proigrat' tri raza, a vyigral vsego lish' odin raz!
- Nevazhno, - uspokoil ee mister Tompkins so snishoditel'noj
uverennost'yu fokusnika. - Vse ravno v samom konce cikla vyigrysh ostanetsya za
nami. Poslednij zapusk ruletki prines mne (po utverzhdeniyu avtora stat'i)
proigrysh v devyat' fishek. Poetomu teper' ya dolzhen pripisat' k uzhe vypisannym
chislam sprava devyatku, posle chego zapis' na moem listke budet vyglyadet' tak:
1 (zacherknuto), 2 (zacherknuto), 3, 4, 5 (zacherknuto), 6, 8 (zacherknuto), 9
Na stol mne nuzhno vylozhit' dvenadcat' (tri plyus devyat') fishek. Na etot
raz vyigrysh ostaetsya za mnoj, poetomu ya vycherkivayu chisla 3 i 9 i, delaya
novuyu stavku, vykladyvayu na stol desyat' (chetyre plyus shest') fishek.
Posleduyushchij vyigrysh zavershaet cikl, tak kak vse chisla, vypisannye na listke
bumagi, okazyvayutsya zacherknutymi. YA stal bogache na shest' fishek, hotya vyigral
v ruletku tol'ko chetyre raza, a proigral pyat' raz!
- A ty dejstvitel'no stal na shest' fishek bogache? - nedoverchivo sprosila
Mod.
- V etom ne mozhet byt' nikakih somnenij. Strategiya postroena tak, chto
vsyakij raz po zavershenii cikla ty, hochesh', ne hochesh', nepremenno vyigryvaesh'
shest' fishek. V etom netrudno ubedit'sya s pomoshch'yu neslozhnyh vychislenij,
poetomu ya nazyvayu etu strategiyu matematicheskoj. Kak vidish', ona
besproigryshna. Esli ugodno, mozhesh' vzyat' listok bumagi i proverit' vse
vykladki sama.
- Veryu tebe na slovo, chto strategiya dejstvitel'no besproigryshna, -
zadumchivo skazala Mod, - no ved' shest' fishchek - ne takoj uzh bol'shoj vyigrysh.
- Kak skazat', - vozrazil mister Tompkins, - ved' vyigrysh shesti fishek v
konce kazhdogo cikla _garantirovan_. Povtoryaya proceduru snova i snova
(nachinaya kazhdyj raz s vypisyvaniya chisel 1, 2, 3), ty mozhesh' vyigrat' skol'ko
tvoej dushe ugodno deneg, a eto sovsem neploho.
- |to prosto velikolepno! - soglasilas' Mod. - Teper' ty smozhesh'
ostavit' sluzhbu v banke, my smozhem pereehat' v bolee prostornuyu kvartiru, a
ne dalee, kak vchera, ya videla v vitrine odnogo mehovogo magazina chudesnoe
manto. I stoit ono kakih-nibud'...
- Razumeetsya, my kupim tebe eto manto, dorogaya, - pospeshil zaverit'
zhenu mister Tompkins. - No snachala nam nuzhno kak mozhno skoree otpravit'sya v
Monte-Karlo. Ved' stat'yu, opublikovannuyu v zhurnale "Esquire", prochitaet
mnozhestvo lyudej, i bylo by ochen' dosadno pribyt' v Monte-Karlo lish' dlya
togo, chtoby zastat' tam schastlivchika, kotoryj operedil nas i dovel kazino do
polnogo razoreniya.
- YA sejchas pozvonyu v aeroport, - predlozhila Mod, - i uznayu, kogda
otpravlyaetsya blizhajshij rejs v Monte-Karlo.
- CHto za speshka? - razdalsya v prihozhej znakomyj golos, i v komnatu
voshel staryj professor. Ostanovivshis' v dveryah, on s udivleniem smotrel na
supruzheskuyu chetu Tompkinsov, neskol'ko razgoryachennyh vnezapno otkryvshimisya
pered nimi perspektivami finansovogo blagopoluchiya.
- My namerevaemsya otpravit'sya blizhajshim zhe rejsom v Monte-Karlo i
nadeemsya vernut'sya osnovatel'no razbogatevshimi, - poyasnil mister Tompkins,
podnimayas' iz kresla navstrechu testyu.
- Ah, vot v chem delo! Togda vse ponyatno, - ulybnulsya professor, s
komfortom ustraivayas' v staromodnom kresle u kamina. - U vas est' novaya
besproigryshnaya strategiya?
- No, papa, eta strategiya dejstvitel'no besproigryshnaya, - s uprekom
skazala Mod, vse eshche derzha ruku na telefonnoj trubke.
- Mod sovershenno prava, - podtverdil mister Tompkins, protyagivaya
professoru zhurnal. - Predlagaemaya strategiya prosto ne mozhet ne vyigrat'!
- Tak-taki i ne mozhet? - ironicheski peresprosil professor s ulybkoj. -
Sejchas uvidim!
Beglo oznakomivshis' so stat'ej, professor prodolzhal:
- Otlichitel'naya osobennost' predlagaemoj strategii sostoit v tom, chto
pravilo, reguliruyushchee velichinu stavok, zastavlyaet vas uvelichivat' stavku
posle kazhdogo proigrysha i snizhat' stavku posle kazhdogo vyigrysha.
Sledovatel'no, esli vy budete poperemenno vyigryvat' i proigryvat', prichem
vyigryshi i proigryshi budut cheredovat'sya s absolyutnoj regulyarnost'yu, to vash
kapital budet kolebat'sya, prichem kazhdoe uvelichenie kapitala budet chut'
bol'she ego umen'sheniya. V etom sluchae vy, nesomnenno, dostatochno skoro
stanete millionerom. No, kak vy ponimaete, absolyutnaya regulyarnost'
vstrechaetsya nechasto. V dejstvitel'nosti veroyatnost' poyavleniya pravil'no
chereduyushchejsya posledovatel'nosti vyigryshej i proigryshej stol' zhe mala, kak i
veroyatnost' poyavleniya odinakovoj po dline serii odnih tol'ko vyigryshej.
Takim obrazom, neobhodimo vyyasnit', chto proizojdet, esli neskol'ko vyigryshej
(ili neskol'ko proigryshej) sleduyut podryad drug za drugom. Esli vam, kak
govoryat igroki, ulybnulas' fortuna, to pravila besproigryshnoj strategii
vynuzhdayut vas libo ponizhat', libo po krajnej mere ne povyshat' stavku posle
kazhdogo vyigrysha, poetomu obshchij vyigrysh okazhetsya ne slishkom bol'shim. S
drugoj storony, te zhe pravila zastavlyayut vas posle kazhdogo proigrysha
povyshat' stavku, poetomu polosa neudach mozhet imet' dlya vas katastroficheskie
posledstviya i dazhe pobudit' vas vyjti iz igry. Krivaya kolebanij vashego
kapitala na etot raz sostoit iz neskol'kih medlenno vozrastayushchih uchastkov,
smenyayushchihsya rezkimi spadami. V nachale igry vy s bol'shej veroyatnost'yu
popadaete na dlinnuyu medlenno vozrastayushchuyu chast' krivoj i v techenie
kakogo-to vremeni naslazhdaetes' priyatnym oshchushcheniem togo, chto vash kapital
medlenno, no neuklonno uvelichivaetsya. No esli vy prodolzhaete igru dostatochno
dolgo v nadezhde na poluchenie vse bol'shej i bol'shej pribyli, to sovershenno
neozhidanno dlya vas vnezapno nastupaet rezkij spad, kotoryj mozhet okazat'sya
dostatochno glubokim dlya togo, chtoby vy, sdelav ocherednuyu stavku, poteryali
poslednij penni. Mozhno pokazat', prichem v sovershenno obshchem vide, chto v
predlagaemoj avtorom stat'i strategii, ravno kak i v lyuboj drugoj vyigryshnoj
strategii, veroyatnost' togo, chto krivaya dostignet dvojnoj otmetki, ravna
veroyatnosti dostignut' nulevogo znacheniya. Inache govorya, vy imeete tochno
takoj zhe shans na okonchatel'nyj vyigrysh, kak esli by postavili vse svoi
den'gi na krasnoe ili chernoe i udvoili svoj kapital ili spustili vse, chto
imeli, za odin-edinstvennyj zapusk ruletki. Vse "besproigryshnye" strategii
sposobny lish' prodlit' igru i tem samym dat' vam vozmozhnost' poluchit' za
svoi den'gi bol'she udovol'stviya. No dazhe esli vy ne trebuete ot igry nichego
bol'shego, to i togda igru ne sleduet tak uslozhnyat'. Kak vy znaete, na obode
kolesa ruletki naneseny tridcat' shest' chisel. Nichto ne meshaet postavit' po
fishke na kazhdoe iz chisel, krome kakogo-nibud' odnogo. V etom sluchae vy
imeete tridcat' pyat' shansov iz tridcati shesti na vyigrysh i na to, chto bank
vyplatit vam za odnu fishku bol'she, chem te tridcat' pyat' fishek, kotorye vy,
delaya stavku, vylozhili na stol. Odnako v odnom iz tridcati shesti zapuskov
ruletochnogo kolesa sharik ostanovitsya na tom chisle, na kotoroe vy reshili ne
stavit' svoyu fishku, i vy poteryaete vse svoi tridcat' pyat' fishek. Esli vy
budete priderzhivat'sya takoj strategii v dostatochno prodolzhitel'noj igre, to
krivaya vashego fluktuiruyushchego kapitala budet vyglyadet' tochno tak zhe, kak
krivaya, kotoruyu vy poluchili, sleduya strategii, predlozhennoj zhurnalom.
Razumeetsya, v svoih rassuzhdeniyah ya ishodil iz predpolozheniya o tom, chto
bank ne predprinimaet nikakih mer, chtoby iskusstvenno ponizit' shansy igroka
na vyigrysh. V dejstvitel'nosti zhe na kazhdom ruletochnom kolese, kotoroe mne
prihodilos' videt', byl nul' - "zero", a inogda dazhe dva nulya, chto ponizhaet
shansy igroka na vyigrysh. Takim obrazom, nezavisimo ot vybrannoj igrokom
strategii ego denezhki malo-pomalu perekochevyvayut iz ego karmana v karman
vladel'ca kazino.
- Vy hotite skazat', - udruchenno progovoril mister Tompkins, - chto
nadezhnoj besproigryshnoj strategii ne sushchestvuet i chto vyigrat' den'gi bez
riska proigrat' s veroyatnost'yu chut' bol'she, chem veroyatnost' vyigrysha, prosto
nevozmozhno?
- Imenno eto ya hotel skazat'! - podtverdil dogadku mistera Tompkinsa
professor. - Bolee togo, vyskazannye mnoj soobrazheniya otnosyatsya ne tol'ko k
takim v sushchnosti pustyakovym problemam, kak azartnye igry, no i ko mnogim
razlichnym fizicheskim yavleniyam, kotorye, na pervyj vzglyad, ne imeyut nikakogo
otnosheniya k veroyatnostnym zakonam. Poetomu esli by vam udalos' izobresti
nadezhnuyu vyigryshnuyu strategiyu dlya preodoleniya zakonov sluchaya, to dlya nee
nashlos' by nemalo gorazdo bolee uvlekatel'nyh primenenij, chem igra na den'gi
v kazino. Naprimer, takaya strategiya pozvolila by sozdavat' avtomashiny,
sposobnye sovershat' probegi lyuboj protyazhennosti bez kapli benzina, stroit'
fabriki, rabotayushchie bez uglya, i osushchestvlyat' mnozhestvo drugih ne menee
fantasticheskih proektov.
- YA gde-to chital o takih fantasticheskih mashinah. Kazhetsya, oni
nazyvayutsya vechnymi dvigatelyami? - zametil mister Tompkins. - Esli ya
pravil'no pomnyu, vechnye dvigateli po zamyslu ih sozdatelej d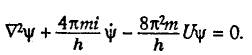
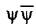 .
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej
.
YA ne stanu sejchas vdavat'sya v detali matematicheskogo vyvoda
fundamental'nogo uravneniya SHredingera. Hochu lish' obratit' vashe vnimanie na
trebovaniya, kotorye priveli k ego vyvodu. Samoe vazhnoe iz etih trebovanij
ves'ma neobychno: _uravnenie dolzhno byt' zapisano v takom vide, chtoby
funkciya, opisyvayushchaya dvizhenie material'nyh chastic, obladala vsemi svojstvami
volny_.
Na neobhodimost' nadelit' dvizhenie material'nyh chastic volnovymi
svojstvami vpervye ukazal francuzskij fizik Lui de Brojl' na osnove svoih
teoreticheskih issledovanij stroeniya atoma. V posleduyushchie gody volnovye
svojstva dvizheniya material'nyh chastic byli nadezhno podtverzhdeny
mnogochislennymi eksperimentami, prodemonstrirovavshimi takie yavleniya, kak
_difrakciya_ puchka elektronov pri prohozhdenii cherez maloe otverstie i
_interferencionnye yavleniya_, proishodyashchie dazhe s takimi sravnitel'no
bol'shimi i slozhnymi chasticami, kak molekuly.
|ksperimental'no ustanovlennye volnovye svojstva material'nyh chastic
byli sovershenno neponyatny s tochki zreniya klassicheskih predstavlenij o
dvizhenii, i de Brojl' byl vynuzhden prinyat' ves'ma neobychnuyu (chtoby ne
skazat' neestestvennuyu) tochku zreniya: po de Brojlyu, vse chasticy
"soprovozhdayutsya" opredelennymi volnami, kotorye, tak skazat', "napravlyayut"
ih dvizheniya.
No kak tol'ko my otkazyvaemsya ot klassicheskih ponyatij i perehodim k
opisaniyu dvizheniya s pomoshch'yu nepreryvnyh funkcij, trebovanie o volnovom
haraktere stanovitsya gorazdo bolee ponyatnym. Ono prosto utverzhdaet, chto
rasprostranenie nashej 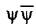 -funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono:
-funkcii analogichno (naprimer) nerasprostraneniyu
tepla skvoz' stenku, nagrevaemuyu s odnoj storony, a rasprostraneniyu skvoz'
tu zhe samuyu stenku mehanicheskoj deformacii (zvuka). Matematicheski eto
oznachaet, chto my ishchem uravnenie opredelennogo (a ne ogranichennogo) vida. |to
fundamental'noe uslovie vmeste s dopolnitel'nym trebovaniem, chtoby nashi
uravneniya, esli ih primenyat' k chasticam bol'shoj massy, perehodili v
uravneniya klassicheskoj mehaniki, poskol'ku kvantovye effekty dlya takih
chastic stanovyatsya prenebrezhimo slabymi, prakticheski svodyat problemu vyvoda
uravneniya k chisto matematicheskomu uprazhneniyu.
Esli vas interesuet, kak vyglyadit okonchatel'nyj otvet - fundamental'noe
uravnenie SHredingera, to ya mogu vypisat' ego. Vot ono: