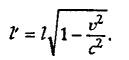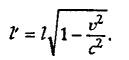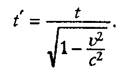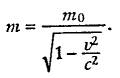izmeryaemye v
razlichnyh dvizhushchihsya sistemah otscheta, mogut rashodit'sya.
Sravnitel'no prostoj matematicheskij analiz etoj problemy, v kotoryj,
odnako, ya ne hotel by vhodit' na etih lekciyah, privodit k vpolne
opredelennym formulam dlya izmeneniya dlin prostranstvennyh i vremenn_y_h
intervalov. Iz nih sleduet, chto lyuboj ob容kt dliny l, dvizhushchijsya
otnositel'no nablyudatelya so skorost'yu u, sokratitsya na velichinu, zavisyashchuyu
ot skorosti, i izmerennaya dlina ob容kta okazhetsya ravnoj
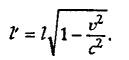 (2)
Analogichno, lyuboj process, dlyashchijsya vremya t, pri nablyudenii iz
dvizhushchejsya otnositel'no nego sistemy otscheta, budet dlit'sya dol'she - vremya
t', kotoroe mozhet byt' vychisleno po formule
(2)
Analogichno, lyuboj process, dlyashchijsya vremya t, pri nablyudenii iz
dvizhushchejsya otnositel'no nego sistemy otscheta, budet dlit'sya dol'she - vremya
t', kotoroe mozhet byt' vychisleno po formule
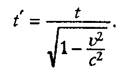 (3)
|to i est' znamenitoe "sokrashchenie prostranstva" i "zamedlenie vremeni"
v teorii otnositel'nosti.
Obychno, kogda skorost' u gorazdo men'she skorosti sveta s, eti effekty
ochen' maly, no pri dostatochno bol'shih skorostyah dliny, nablyudaemye iz
dvizhushchejsya sistemy otscheta, mogut byt' sdelany skol' ugodno malymi, a
vremenn_y_e intervaly - skol' ugodno prodolzhitel'nymi.
YA hochu, chtoby vy ne zabyvali, chto oba effekta - i sokrashchenie
prostranstvennyh intervalov, i zamedlenie vremeni - sovershenno simmetrichny
i, esli passazhiry bystro mchashchegosya poezda budut udivlyat'sya, pochemu passazhiry
stoyashchego poezda takie toshchie i dvizhutsya tak medlenno, passazhiry stoyashchego
poezda budut razmyshlyat' o tom zhe, glyadya na passazhirov mchashchegosya poezda.
Eshche odno sledstvie sushchestvovaniya maksimal'noj dostizhimoj skorosti
otnositsya k masse dvizhushchihsya tel. Kak yavstvuet iz obshchih osnov mehaniki,
massa tela opredelyaet, naskol'ko trudno privesti ego v dvizhenie ili, esli
ono uzhe dvizhetsya, uskorit' ego: chem bol'she massa, tem trudnee uvelichit'
skorost' tela na dannuyu velichinu.
To, chto ni odno telo ni pri kakih obstoyatel'stvah ne mozhet dvigat'sya so
skorost'yu, bol'shej skorosti sveta, privodit nas neposredstvenno k vyvodu,
chto ego soprotivlenie dal'nejshemu uskoreniyu, ili, inache govorya, ego massa,
neogranichenno vozrastaet, kogda skorost' tela priblizhaetsya k skorosti sveta.
Matematicheskij analiz pozvolyaet vyvesti formulu zavisimosti massy tela ot
ego skorosti, analogichnuyu formulam (2) i (3). Esli m0 - massa tela pri ochen'
malyh skorostyah, to massa m tela pri skorosti u opredelyaetsya po formule
(3)
|to i est' znamenitoe "sokrashchenie prostranstva" i "zamedlenie vremeni"
v teorii otnositel'nosti.
Obychno, kogda skorost' u gorazdo men'she skorosti sveta s, eti effekty
ochen' maly, no pri dostatochno bol'shih skorostyah dliny, nablyudaemye iz
dvizhushchejsya sistemy otscheta, mogut byt' sdelany skol' ugodno malymi, a
vremenn_y_e intervaly - skol' ugodno prodolzhitel'nymi.
YA hochu, chtoby vy ne zabyvali, chto oba effekta - i sokrashchenie
prostranstvennyh intervalov, i zamedlenie vremeni - sovershenno simmetrichny
i, esli passazhiry bystro mchashchegosya poezda budut udivlyat'sya, pochemu passazhiry
stoyashchego poezda takie toshchie i dvizhutsya tak medlenno, passazhiry stoyashchego
poezda budut razmyshlyat' o tom zhe, glyadya na passazhirov mchashchegosya poezda.
Eshche odno sledstvie sushchestvovaniya maksimal'noj dostizhimoj skorosti
otnositsya k masse dvizhushchihsya tel. Kak yavstvuet iz obshchih osnov mehaniki,
massa tela opredelyaet, naskol'ko trudno privesti ego v dvizhenie ili, esli
ono uzhe dvizhetsya, uskorit' ego: chem bol'she massa, tem trudnee uvelichit'
skorost' tela na dannuyu velichinu.
To, chto ni odno telo ni pri kakih obstoyatel'stvah ne mozhet dvigat'sya so
skorost'yu, bol'shej skorosti sveta, privodit nas neposredstvenno k vyvodu,
chto ego soprotivlenie dal'nejshemu uskoreniyu, ili, inache govorya, ego massa,
neogranichenno vozrastaet, kogda skorost' tela priblizhaetsya k skorosti sveta.
Matematicheskij analiz pozvolyaet vyvesti formulu zavisimosti massy tela ot
ego skorosti, analogichnuyu formulam (2) i (3). Esli m0 - massa tela pri ochen'
malyh skorostyah, to massa m tela pri skorosti u opredelyaetsya po formule
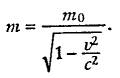 (4)
My vidim, chto soprotivlenie tela dal'nejshemu uskoreniyu stanovitsya
beskonechno bol'shim, kogda i stremitsya k c. |tot effekt relyativistskogo
izmeneniya massy mozhet byt' legko nablyudaem eksperimental'no na chasticah,
dvizhushchihsya s ochen' bol'shimi skorostyami. Naprimer, massa elektronov,
ispuskaemyh radioaktivnymi telami (so skorost'yu, sostavlyayushchej 99 % skorosti
sveta), v neskol'ko raz bol'she, chem v sostoyanii pokoya, a massy elektronov,
obrazuyushchih tak nazyvaemye kosmicheskie livni i neredko dvizhushchihsya so
skorost'yu 99,98 % skorosti sveta, v 1000 raz bol'she. K takim skorostyam
klassicheskaya mehanika stanovitsya absolyutno neprimenimoj, i my vstupaem v
oblast' chistoj teorii otnositel'nosti.
�Glava 3�
Mister Tompkins beret otpusk
Misteru Tompkinsu ochen' ponravilis' priklyucheniya v relyativistskom
gorode, ogorchalo tol'ko, chto s nim ne bylo professora, kotoryj mog by
ob座asnit' neobychnye yavleniya, kotorye emu, misteru Tompkinsu, dovelos' tam
nablyudat', naprimer, pomoch' razreshit' zagadku, osobenno zanimavshuyu ego:
kakim obrazom tormoznomu konduktoru udavalos' predupredit' starenie
passazhirov? Mnogo nochej podryad mister Tompkins ukladyvalsya v postel' s
nadezhdoj snova uvidet' polyubivshijsya emu gorod, no sny mister Tompkins videl
redko i, v osnovnom, dovol'no nepriyatnye. Naprimer, v poslednij raz misteru
Tompkinsu prisnilos', chto upravlyayushchij bankom uvolil ego za nebrezhnost' v
vedenii bankovskih schetov. Prosnuvshis', mister Tompkins schel za blago vzyat'
otpusk i otpravit'sya na nedel'ku kuda-nibud' na more. Tak mister Tompkins
okazalsya v kupe poezda, nablyudaya v okno, kak serye kryshi prigoroda
postepenno ustupayut mesto zelenym luzhajkam sel'skoj mestnosti. Mister
Tompkins dostal gazetu i popytalsya sosredotochit'sya na poslednih
korrespondenciyah s teatra voennyh dejstvij vo V'etname. No vse soobshcheniya
pokazalis' emu nevynosimo skuchnymi, a zheleznodorozhnyj vagon tak priyatno
pokachivalo...
Kogda Tompkins opustil gazetu i snova vyglyanul v okno, pejzazh sil'no
izmenilsya. Telegrafnye stolby stoyali tak blizko drug ot druga, chto
napominali gigantskuyu izgorod', a krony derev'ev byli takimi uzkimi, chto
derev'ya napominali ital'yanskie kiparisy. Naprotiv mistera Tompkinsa v kupe
sidel ego staryj znakomyj - professor i s zhivejshim interesom smotrel v okno.
Po-vidimomu, on voshel v kupe, poka mister Tompkins byl zanyat chteniem gazety.
- My nahodimsya v strane otnositel'nosti, esli ya ne oshibayus', - zametil
mister Tompkins.
- O! - voskliknul professor. - Ne ozhidal vstretit' poputchika,
obladayushchego stol' glubokimi poznaniyami! A po kakomu uchebniku vy izuchali
teoriyu otnositel'nosti?
- Mne uzhe dovodilos' byvat' zdes', hotya ya ne imel chesti byt' vashim
poputchikom.
- Na etot raz vam pridetsya byt' moim gidom, - skazal staryj professor.
- Boyus', chto mne pridetsya otkazat'sya ot etoj pochetnoj roli, - otklonil
lestnoe predlozhenie mister Tompkins. - YA dejstvitel'no videl mnozhestvo
neobychnyh veshchej, no mestnye zhiteli, k kotorym ya obrashchalsya za raz座asneniyami,
nikak ne mogli vzyat' v tolk, chto menya smushchaet.
- Vpolne estestvenno, - zametil professor. - Ved' oni rodilis' v etom
mire, i vse proishodyashchie vokrug nih yavleniya kazhutsya im samoochevidnymi.
Predstavlyayu, kak oni udivilis' by, esli by im dovelos' pobyvat' v tom mire,
gde privykli zhit' vy. Dumayu, on pokazalsya by im ves'ma neobychnym.
- Pozvol'te zadat' vam odin vopros, - skazal mister Tompkins. - V
proshlyj raz, kogda ya byl zdes', mne vstretilsya tormoznoj konduktor s
zheleznoj dorogi. On utverzhdal, budto iz-za togo, chto poezd ostanavlivaetsya i
trogaetsya v put', passazhiry staryatsya bystree, chem lyudi v gorode. CHto eto -
chudesa ili yavlenie, kotoroe soglasuetsya s sovremennoj naukoj?
- Ssylat'sya na chudesa pri ob座asnenii chego ugodno - priem zapreshchennyj, -
otvetil professor. - YAvlenie, o kotorom govoril vash konduktor, sleduet iz
zakonov fiziki. Analiziruya novye (ili, luchshe skazat', starye, no lish'
nezadolgo do togo otkrytye) ponyatiya prostranstva i vremeni, |jnshtejn
pokazal, chto vse fizicheskie processy zamedlyayutsya, kogda sistema, v kotoroj
oni proishodyat, izmenyaet svoyu skorost'. V nashem mire takie effekty pochti
nezametny, no zdes' iz-za maloj skorosti sveta oni stanovyatsya legko
nablyudaemymi. Naprimer, esli vy popytaetes' zdes' svarit' sebe na zavtrak
yajco i vmesto togo, chtoby dat' kastryul'ke spokojno stoyat' na ogne, nachnete
dvigat' ee to v odnu, to v druguyu storonu, to svarit' yajco vkrutuyu vam
udastsya ne za pyat', a, skazhem, za shest' minut. Vse processy v chelovecheskom
tele takzhe zamedlyayutsya, esli, naprimer, chelovek kachaetsya v kresle-kachalke
ili sidit v kupe poezda, kotoryj zamedlyaet ili uskoryaet hod: v takogo roda
usloviyah my zhivem medlennee. No poskol'ku vse processy zamedlyayutsya
odinakovo, fiziki predpochitayut govorit', chto v _neravnomerno dvizhushchejsya
sisteme vremya techet medlennee_.
- A nablyudayut li takie yavleniya uchenye v nashem mire, tak skazat', u nas
doma?
- Nablyudayut, hotya dlya etogo im prihoditsya proyavlyat' nedyuzhinnoe
eksperimental'noe iskusstvo. Tehnicheski ochen' trudno dostich' neobhodimyh
uskorenij, a fizicheskie usloviya v neravnomerno dvizhushchejsya sisteme
analogichny, ya by dazhe skazal "tozhdestvenny", rezul'tatu vozdejstviya ochen'
bol'shoj sily tyazhesti. Vam, dolzhno byt', prihodilos' zamechat', chto v kabine
podnimayushchegosya s uskoreniem lifta vam kazhetsya, chto vy stanovites' tyazhelee.
Naoborot, esli lift opuskaetsya (naprimer, esli oborvalsya tros i lift
padaet), to vy oshchushchaete kak by poteryu vesa. Ob座asnenie izmenenij vesa
sostoit v tom, chto sozdavaemoe uskoreniem gravitacionnoe pole dobavlyaetsya
ili vychitaetsya iz sily tyazhesti Zemli. Potencial sily tyazhesti na Solnce vo
mnogo raz bol'she, chem na poverhnosti Zemli, i poetomu vse processy na Solnce
nemnogo zamedlyayutsya. Astronomy nablyudayut eto.
- No ved' oni ne mogut otpravit'sya na Solnce, chtoby nablyudat'
zamedlenie vseh processov?
- Im i ne nuzhno tuda otpravlyat'sya. Oni nablyudayut svet, prihodyashchij k nam
ot Solnca. |tot svet porozhdaetsya kolebaniyami razlichnyh atomov v solnechnoj
atmosfere. Esli vse processy na Solnce idut medlennee, to skorost' atomnyh
kolebanij takzhe ubyvaet i, sravnivaya svet, ispuskaemyj Solncem i zemnymi
istochnikami, astronomy mogut zametit' raznicu.
- Kstati, vy ne znaete, kak nazyvaetsya nebol'shaya stanciya, mimo kotoroj
my sejchas proezzhaem? - prerval sebya professor.
Poezd katilsya vdol' perrona malen'koj zaholustnoj stancii. Perron byl
sovershenno pust, esli ne schitat' nachal'nika stancii i molodogo nosil'shchika,
sidevshego na bagazhnoj telezhke i chitavshego gazetu. Vdrug nachal'nik stancii
kak-to nelepo vzmahnul rukami i upal nichkom. Mister Tomkins ne slyshal zvuka
vystrela, dolzhno byt', zaglushennogo stukom koles poezda, no luzha krovi u
tela nachal'nika stancii ne ostavlyala somnenij v tom, chto proizoshlo ubijstvo.
Professor ne medlya dernul stop-kran, i poezd ryvkom ostanovilsya. Kogda
mister Tompkins i professor vyshli iz vagona, nosil'shchik bezhal k telu i na
perrone poyavilsya mestnyj polismen.
- Ubit vystrelom v serdce, - konstatiroval polismen, osmotrev telo, i,
polozhiv tyazheluyu ruku na plecho nosil'shchika, prodolzhil:
- Vy arestovany za ubijstvo nachal'nika stancii.
- Ne ubival ya ego, - zakrichal neschastnyj nosil'shchik. - YA chital gazetu,
kak vdrug uslyshal vystrel. Vozmozhno, eti dzhentl'meny s poezda videli, kak
vse proizoshlo i mogut podtverdit', chto ya ne vinoven.
- Dejstvitel'no, - podtverdil mister Tompkins, - ya videl svoimi
sobstvennymi glazami, kak etot chelovek chital gazetu v tot moment, kogda byl
zastrelen nachal'nik stancii. Mogu poklyast'sya na Biblii.
- No vy nahodilis' v dvizhushchemsya poezde, - zametil polismen, obretaya
nachal'stvennyj ton, - i poetomu vashi pokazaniya ne imeyut dokazatel'noj sily.
S tochki zreniya nablyudatelya na perrone etot chelovek mog byt' zastrelen v tot
zhe samyj moment. Razve vy ne znaete, chto odnovremennost' sobytij zavisit ot
sistemy otscheta, iz kotoroj vy ee nablyudaete? Projdem bez lishnego shuma, -
obratilsya on k nosil'shchiku.
- Proshu izvinit' menya, konstebl', - prerval ego professor, - no vy
sovershenno ne pravy i ya ne dumayu, chto v policejskom upravlenii ochen'
obraduyutsya, uznav o vashem nevezhestve. Nikto ne sporit: v vashej strane
ponyatie odnovremennosti v vysshej stepeni otnositel'no. |to pravda. Verno i
to, chto dva sobytiya, proishodyashchih v razlichnyh mestah, mogut byt'
odnovremennymi ili ne odnovremennymi v zavisimosti ot dvizheniya nablyudatelya.
No dazhe v vashej strane ni odin nablyudatel' ne mozhet videt' sledstvie ran'she,
chem prichinu. Vam zhe nikogda ne sluchalos' poluchat' telegrammu do togo, kak ta
byla otpravlena, ved' verno? Ne sluchalos' i pit' do togo, kak butylku
otkuporili. Naskol'ko ya vas ponimayu, vy polagaete, chto iz-za dvizheniya poezda
my, passazhiry, nablyudali vystrel gorazdo _pozzhe_, chem ego sledstvie,
poskol'ku, vyskochiv iz vagona totchas zhe posle ekstrennoj ostanovki poezda,
my uvideli nachal'nika stancii lezhashchim na zemle, no eshche ne videli samogo
vystrela. YA znayu, chto v policii vas uchat verit' tol'ko tomu, chto napisano v
vashih instrukciyah. Vzglyanite v nih i vy, veroyatno, otyshchite chto-nibud'
podhodyashchee k sluchayu.
Ton professora proizvel neizgladimoe vpechatlenie na polismena i,
vytashchiv karmannyj svod instrukcij, on prinyalsya medlenno, stranica za
stranicej izuchat' ih. Vskore po ego shirokoj krasnoj fizionomii razlilas'
ulybka oblegcheniya.
- Vot, - skazal on, - razdel 37, chast' 12, paragraf e: "V kachestve
absolyutno nadezhnogo alibi sleduet schitat' lyuboe avtoritetnoe dokazatel'stvo
togo, chto iz lyuboj dvizhushchejsya sistemy otscheta v moment soversheniya
prestupleniya ili v techenie intervala vremeni +-cd (gde s - skorost' sveta, a
d - rasstoyanie ot mesta prestupleniya) podozrevaemogo videli v drugom meste".
- Vy svobodny, moj milyj, - obratilsya polismen k nosil'shchiku i dobavil,
povernuvshis' k professoru:
- Ochen' priznatelen vam, ser, chto vy izbavili menya ot nepriyatnostej s
policejskim upravleniem. YA v policii sluzhu nedavno i eshche ne vyuchil nazubok
vse pravila. No mne vse ravno neobhodimo dolozhit' ob ubijstve. I polismen
pospeshil k telefonnoj budke. CHerez minutu on zakrichal na ves' perron:
- Vse v poryadke! Oni pojmali nastoyashchego ubijcu, kogda tot bezhal so
stancii. Eshche raz blagodaryu vas, ser!
- Dolzhno byt', ya neprohodimo glup, - zametil mister Tompkins, kogda
poezd snova tronulsya, - no chto oznachaet vsya eta nerazberiha s
odnovremennost'yu? Imeet li odnovremennost' voobshche kakoj-nibud' smysl v etoj
strane?
- Imeet, - glasil otvet professora, - no lish' v opredelennoj stepeni,
inache ya ne smog by pomoch' bednyage-nosil'shchiku. Delo v tom, chto esli
sushchestvuet estestvennyj predel skorosti dlya dvizheniya lyubogo tela ili
rasprostraneniya lyubogo signala, to odnovremennost' v obychnom smysle etogo
slova utrachivaet smysl. Vam, veroyatno, budet legche ponyat' sut' dela na
sleduyushchem primere. Predpolozhim, chto u vas est' drug, zhivushchij v dalekom
gorode, s kotorym vy perepisyvaetes', i pochtovyj poezd, kotoryj otpravlyaetsya
raz v sutki, - samoe bystroe sredstvo soobshcheniya. Predpolozhim teper', chto
kakoe-to proisshestvie sluchilos' s vami v voskresen'e i vy uznali, chto
analogichnoe proisshestvie dolzhno proizojti s vashim drugom. YAsno, chto vy ne
mozhete uvedomit' ego ob etom ran'she vtornika. S drugoj storony, esli by on
znal zaranee o tom, chto proizojdet s vami, to poslednij den', kogda on mog
predupredit' vas o gryadushchem sobytii, byl chetverg na proshloj nedele. Takim
obrazom, v techenie shesti dnej - s chetverga na proshloj nedele do vtornika na
budushchej nedele - vash drug ne sposoben ni povliyat' na vashu sud'bu v
voskresen'e, ni uznat' o tom, chto s vami proizoshlo. S tochki zreniya
prichinnosti on iz座at iz obshcheniya s vami, ili, tak skazat', ekskommunicirovan.
- A chto esli emu poslat' telegrammu? - predlozhil mister Tompkins.
- No ved' ya predpolozhil, chto skorost' pochtovogo poezda - maksimal'no
vozmozhnaya. Primerno tak i obstoit delo v etoj strane. U nas na rodine
maksimal'noj skorost'yu yavlyaetsya skorost' sveta, i vy ne mozhete poslat'
signal, kotoroj rasprostranyalsya by bystree, chem radiosignal.
- Pust' tak, - soglasilsya mister Tompkins, - no dazhe esli nichto ne
mozhet prevzojti skorost' pochtovogo poezda, ya vse ravno ne ponimayu, kakoe eto
imeet otnoshenie k odnovremennosti. Moj drug i ya po-prezhnemu obedaem po
voskresen'yam v odno i to zhe vremya. Razve ne tak?
- Net, ne tak. Vashe utverzhdenie voobshche ne imelo by smysla: odin
nablyudatel' soglasilsya by s tem, chto vy s priyatelem obedaete odnovremenno, a
drugie nablyudateli, proizvodivshie svoi nablyudeniya iz drugih poezdov,
utverzhdali by, chto vy obedaete po voskresen'yam v to samoe vremya, kogda vash
drug zavtrakaet po pyatnicam ili uzhinaet po vtornikam. No nikto ne mozhet
nablyudat' vas i vashego druga za odnovremennoj trapezoj, esli vas razdelyaet
vremennoj interval bolee treh dnej.
- No kak eto mozhet byt'? - voskliknul nedoverchivo mister Tompkins.
- Proishodit vse eto tochno tak, kak vy, vozmozhno, uyasnili sebe iz moih
lekcij. Verhnij predel skorosti dolzhen ostavat'sya odnim i tem zhe pri
nablyudenii iz razlichnyh dvizhushchihsya sistem otscheta. Prinyav takoe
predpolozhenie, my s neobhodimost'yu prihodim k zaklyucheniyu o tom, chto...
Tut razgovor, k sozhaleniyu, prervalsya, tak kak poezd pribyl na tu
stanciyu, gde misteru Tompkinsu nuzhno bylo shodit'.
Kogda mister Tompkins spustilsya k zavtraku na dlinnuyu zasteklennuyu
verandu otelya na sleduyushchee utro posle svoego pribytiya na poberezh'e, ego
ozhidal priyatnyj syurpriz: na protivopolozhnom konce stola protiv nego vossedal
staryj professor s krasivoj molodoj devushkoj, kotoraya ozhivlenno chto-to
govorila emu, chasto poglyadyvaya v tu storonu, gde sidel mister Tompkins.
- Dolzhno byt', ya sovershil bol'shuyu glupost', kogda zasnul v poezde, -
podumal mister Tompkins, serdyas' na sebya vse bol'she i bol'she, - a professor
vse eshche pomnit tot glupyj vopros, kotoryj ya zadal emu o molodeyushchih
passazhirah. No po krajnej mere eto pozvolyaet mne prodolzhit' znakomstvo s
professorom i rassprosit' ego o tom, chto mne po-prezhnemu neponyatno.
Dazhe samomu sebe mister Tompkins ne hotel priznat'sya, chto dumaet ne
tol'ko o professore, no i o ego horoshen'koj sputnice.
- Da, da, konechno, ya pomnyu, chto videl vas na svoih lekciyah, - skazal
professor, kogda oni vyhodili iz obedennogo zala. - Poznakom'tes', eto moya
doch' Mod. Ona zanimaetsya zhivopis'yu.
- Rad poznakomit'sya s vami, miss Mod, - otvetil mister Tompkins i
podumal, chto nikogda ne slyshal bolee krasivogo imeni. - Dumayu, chto zdeshnie
krasoty dadut vam nemalo materiala dlya vashih etyudov.
- Mod nepremenno pokazhet ih vam kogda-nibud', - poobeshchal professor. - A
sejchas skazhite mne luchshe, mnogo li vy pocherpnuli iz moej lekcii?
- O da, ochen' mnogo! Bolee togo, ya na sebe prochuvstvoval vse eti
relyativistskie sokrashcheniya material'nyh ob容ktov i sumasshedshee povedenie
chasov, kogda pobyval v gorode, gde skorost' sveta sostavlyala tol'ko
kilometrov desyat' v chas.
- ZHal', chto vy propustili moyu sleduyushchuyu lekciyu o krivizne prostranstva
i ee svyazi s silami n'yutonovskoj gravitacii, - zadumchivo proiznes professor.
- No zdes', na poberezh'e, u nas hvatit vremeni, i ya nadeyus' ob座asnit' vam
vse eto. Naprimer, ponimaete li vy, v chem raznica mezhdu polozhitel'noj i
otricatel'noj kriviznoj prostranstva?
- Papochka, - vmeshalas' miss Mod, kaprizno naduv guby, - esli vy
sobiraetes' snova besedovat' o fizike, to ya luchshe zajmus' etyudami.
- Horosho, devochka, idi, - soglasilsya professor, opuskayas' v legkoe
kreslo. - YA vizhu, chto vy molodoj chelovek, ne ochen' svedushchi v matematike, no
dumayu, chto udastsya ob座asnit' vam vse ochen' prosto. Dlya bol'shej naglyadnosti ya
budu govorit' o poverhnosti. Predstav'te sebe, chto mister SHell (vy znaete, o
kom ya govoryu, - eto tot samyj gospodin, kotoryj vladeet benzozapravochnymi
stanciyami "SHell Ojl") reshil kak-to raz prosledit' za tem, chtoby ego
zapravochnye stancii byli ravnomerno raspredeleny po territorii kakoj-nibud'
strany, naprimer, Ameriki. Dlya etogo mister SHell otdal pravleniyu svoej
firmy, raspolozhennomu gde-to v centre strany (esli ya ne oshibayus', mnogie
sklonny dumat', chto serdce Ameriki nahoditsya v Kanzas-Siti), rasporyazhenie
soschitat' chislo stancij na rasstoyanii sto, dvesti, trista i t. d. mil' ot
centra. So shkol'noj skam'i mister SHell vynes vospominaniya o tom, chto ploshchad'
kruga proporcional'na kvadratu ego radiusa, i ozhidaet, chto v sluchae
ravnomernogo raspredeleniya zapravochnyh stancij chislo ih v rezul'tate
podschetov budet vozrastat', kak posledovatel'nost' chisel 1; 4; 9; 16 i t.d.
Kogda v pravlenie "SHell Ojl" stali postupat' otchety, glava firmy k svoemu
velikomu udivleniyu obnaruzhil, chto chislo stancij vozrastaet gorazdo
medlennee, naprimer, kak chisla, obrazuyushchie posledovatel'nost' 1; 3,8; 8,5;
15,0 i t.d.
(4)
My vidim, chto soprotivlenie tela dal'nejshemu uskoreniyu stanovitsya
beskonechno bol'shim, kogda i stremitsya k c. |tot effekt relyativistskogo
izmeneniya massy mozhet byt' legko nablyudaem eksperimental'no na chasticah,
dvizhushchihsya s ochen' bol'shimi skorostyami. Naprimer, massa elektronov,
ispuskaemyh radioaktivnymi telami (so skorost'yu, sostavlyayushchej 99 % skorosti
sveta), v neskol'ko raz bol'she, chem v sostoyanii pokoya, a massy elektronov,
obrazuyushchih tak nazyvaemye kosmicheskie livni i neredko dvizhushchihsya so
skorost'yu 99,98 % skorosti sveta, v 1000 raz bol'she. K takim skorostyam
klassicheskaya mehanika stanovitsya absolyutno neprimenimoj, i my vstupaem v
oblast' chistoj teorii otnositel'nosti.
�Glava 3�
Mister Tompkins beret otpusk
Misteru Tompkinsu ochen' ponravilis' priklyucheniya v relyativistskom
gorode, ogorchalo tol'ko, chto s nim ne bylo professora, kotoryj mog by
ob座asnit' neobychnye yavleniya, kotorye emu, misteru Tompkinsu, dovelos' tam
nablyudat', naprimer, pomoch' razreshit' zagadku, osobenno zanimavshuyu ego:
kakim obrazom tormoznomu konduktoru udavalos' predupredit' starenie
passazhirov? Mnogo nochej podryad mister Tompkins ukladyvalsya v postel' s
nadezhdoj snova uvidet' polyubivshijsya emu gorod, no sny mister Tompkins videl
redko i, v osnovnom, dovol'no nepriyatnye. Naprimer, v poslednij raz misteru
Tompkinsu prisnilos', chto upravlyayushchij bankom uvolil ego za nebrezhnost' v
vedenii bankovskih schetov. Prosnuvshis', mister Tompkins schel za blago vzyat'
otpusk i otpravit'sya na nedel'ku kuda-nibud' na more. Tak mister Tompkins
okazalsya v kupe poezda, nablyudaya v okno, kak serye kryshi prigoroda
postepenno ustupayut mesto zelenym luzhajkam sel'skoj mestnosti. Mister
Tompkins dostal gazetu i popytalsya sosredotochit'sya na poslednih
korrespondenciyah s teatra voennyh dejstvij vo V'etname. No vse soobshcheniya
pokazalis' emu nevynosimo skuchnymi, a zheleznodorozhnyj vagon tak priyatno
pokachivalo...
Kogda Tompkins opustil gazetu i snova vyglyanul v okno, pejzazh sil'no
izmenilsya. Telegrafnye stolby stoyali tak blizko drug ot druga, chto
napominali gigantskuyu izgorod', a krony derev'ev byli takimi uzkimi, chto
derev'ya napominali ital'yanskie kiparisy. Naprotiv mistera Tompkinsa v kupe
sidel ego staryj znakomyj - professor i s zhivejshim interesom smotrel v okno.
Po-vidimomu, on voshel v kupe, poka mister Tompkins byl zanyat chteniem gazety.
- My nahodimsya v strane otnositel'nosti, esli ya ne oshibayus', - zametil
mister Tompkins.
- O! - voskliknul professor. - Ne ozhidal vstretit' poputchika,
obladayushchego stol' glubokimi poznaniyami! A po kakomu uchebniku vy izuchali
teoriyu otnositel'nosti?
- Mne uzhe dovodilos' byvat' zdes', hotya ya ne imel chesti byt' vashim
poputchikom.
- Na etot raz vam pridetsya byt' moim gidom, - skazal staryj professor.
- Boyus', chto mne pridetsya otkazat'sya ot etoj pochetnoj roli, - otklonil
lestnoe predlozhenie mister Tompkins. - YA dejstvitel'no videl mnozhestvo
neobychnyh veshchej, no mestnye zhiteli, k kotorym ya obrashchalsya za raz座asneniyami,
nikak ne mogli vzyat' v tolk, chto menya smushchaet.
- Vpolne estestvenno, - zametil professor. - Ved' oni rodilis' v etom
mire, i vse proishodyashchie vokrug nih yavleniya kazhutsya im samoochevidnymi.
Predstavlyayu, kak oni udivilis' by, esli by im dovelos' pobyvat' v tom mire,
gde privykli zhit' vy. Dumayu, on pokazalsya by im ves'ma neobychnym.
- Pozvol'te zadat' vam odin vopros, - skazal mister Tompkins. - V
proshlyj raz, kogda ya byl zdes', mne vstretilsya tormoznoj konduktor s
zheleznoj dorogi. On utverzhdal, budto iz-za togo, chto poezd ostanavlivaetsya i
trogaetsya v put', passazhiry staryatsya bystree, chem lyudi v gorode. CHto eto -
chudesa ili yavlenie, kotoroe soglasuetsya s sovremennoj naukoj?
- Ssylat'sya na chudesa pri ob座asnenii chego ugodno - priem zapreshchennyj, -
otvetil professor. - YAvlenie, o kotorom govoril vash konduktor, sleduet iz
zakonov fiziki. Analiziruya novye (ili, luchshe skazat', starye, no lish'
nezadolgo do togo otkrytye) ponyatiya prostranstva i vremeni, |jnshtejn
pokazal, chto vse fizicheskie processy zamedlyayutsya, kogda sistema, v kotoroj
oni proishodyat, izmenyaet svoyu skorost'. V nashem mire takie effekty pochti
nezametny, no zdes' iz-za maloj skorosti sveta oni stanovyatsya legko
nablyudaemymi. Naprimer, esli vy popytaetes' zdes' svarit' sebe na zavtrak
yajco i vmesto togo, chtoby dat' kastryul'ke spokojno stoyat' na ogne, nachnete
dvigat' ee to v odnu, to v druguyu storonu, to svarit' yajco vkrutuyu vam
udastsya ne za pyat', a, skazhem, za shest' minut. Vse processy v chelovecheskom
tele takzhe zamedlyayutsya, esli, naprimer, chelovek kachaetsya v kresle-kachalke
ili sidit v kupe poezda, kotoryj zamedlyaet ili uskoryaet hod: v takogo roda
usloviyah my zhivem medlennee. No poskol'ku vse processy zamedlyayutsya
odinakovo, fiziki predpochitayut govorit', chto v _neravnomerno dvizhushchejsya
sisteme vremya techet medlennee_.
- A nablyudayut li takie yavleniya uchenye v nashem mire, tak skazat', u nas
doma?
- Nablyudayut, hotya dlya etogo im prihoditsya proyavlyat' nedyuzhinnoe
eksperimental'noe iskusstvo. Tehnicheski ochen' trudno dostich' neobhodimyh
uskorenij, a fizicheskie usloviya v neravnomerno dvizhushchejsya sisteme
analogichny, ya by dazhe skazal "tozhdestvenny", rezul'tatu vozdejstviya ochen'
bol'shoj sily tyazhesti. Vam, dolzhno byt', prihodilos' zamechat', chto v kabine
podnimayushchegosya s uskoreniem lifta vam kazhetsya, chto vy stanovites' tyazhelee.
Naoborot, esli lift opuskaetsya (naprimer, esli oborvalsya tros i lift
padaet), to vy oshchushchaete kak by poteryu vesa. Ob座asnenie izmenenij vesa
sostoit v tom, chto sozdavaemoe uskoreniem gravitacionnoe pole dobavlyaetsya
ili vychitaetsya iz sily tyazhesti Zemli. Potencial sily tyazhesti na Solnce vo
mnogo raz bol'she, chem na poverhnosti Zemli, i poetomu vse processy na Solnce
nemnogo zamedlyayutsya. Astronomy nablyudayut eto.
- No ved' oni ne mogut otpravit'sya na Solnce, chtoby nablyudat'
zamedlenie vseh processov?
- Im i ne nuzhno tuda otpravlyat'sya. Oni nablyudayut svet, prihodyashchij k nam
ot Solnca. |tot svet porozhdaetsya kolebaniyami razlichnyh atomov v solnechnoj
atmosfere. Esli vse processy na Solnce idut medlennee, to skorost' atomnyh
kolebanij takzhe ubyvaet i, sravnivaya svet, ispuskaemyj Solncem i zemnymi
istochnikami, astronomy mogut zametit' raznicu.
- Kstati, vy ne znaete, kak nazyvaetsya nebol'shaya stanciya, mimo kotoroj
my sejchas proezzhaem? - prerval sebya professor.
Poezd katilsya vdol' perrona malen'koj zaholustnoj stancii. Perron byl
sovershenno pust, esli ne schitat' nachal'nika stancii i molodogo nosil'shchika,
sidevshego na bagazhnoj telezhke i chitavshego gazetu. Vdrug nachal'nik stancii
kak-to nelepo vzmahnul rukami i upal nichkom. Mister Tomkins ne slyshal zvuka
vystrela, dolzhno byt', zaglushennogo stukom koles poezda, no luzha krovi u
tela nachal'nika stancii ne ostavlyala somnenij v tom, chto proizoshlo ubijstvo.
Professor ne medlya dernul stop-kran, i poezd ryvkom ostanovilsya. Kogda
mister Tompkins i professor vyshli iz vagona, nosil'shchik bezhal k telu i na
perrone poyavilsya mestnyj polismen.
- Ubit vystrelom v serdce, - konstatiroval polismen, osmotrev telo, i,
polozhiv tyazheluyu ruku na plecho nosil'shchika, prodolzhil:
- Vy arestovany za ubijstvo nachal'nika stancii.
- Ne ubival ya ego, - zakrichal neschastnyj nosil'shchik. - YA chital gazetu,
kak vdrug uslyshal vystrel. Vozmozhno, eti dzhentl'meny s poezda videli, kak
vse proizoshlo i mogut podtverdit', chto ya ne vinoven.
- Dejstvitel'no, - podtverdil mister Tompkins, - ya videl svoimi
sobstvennymi glazami, kak etot chelovek chital gazetu v tot moment, kogda byl
zastrelen nachal'nik stancii. Mogu poklyast'sya na Biblii.
- No vy nahodilis' v dvizhushchemsya poezde, - zametil polismen, obretaya
nachal'stvennyj ton, - i poetomu vashi pokazaniya ne imeyut dokazatel'noj sily.
S tochki zreniya nablyudatelya na perrone etot chelovek mog byt' zastrelen v tot
zhe samyj moment. Razve vy ne znaete, chto odnovremennost' sobytij zavisit ot
sistemy otscheta, iz kotoroj vy ee nablyudaete? Projdem bez lishnego shuma, -
obratilsya on k nosil'shchiku.
- Proshu izvinit' menya, konstebl', - prerval ego professor, - no vy
sovershenno ne pravy i ya ne dumayu, chto v policejskom upravlenii ochen'
obraduyutsya, uznav o vashem nevezhestve. Nikto ne sporit: v vashej strane
ponyatie odnovremennosti v vysshej stepeni otnositel'no. |to pravda. Verno i
to, chto dva sobytiya, proishodyashchih v razlichnyh mestah, mogut byt'
odnovremennymi ili ne odnovremennymi v zavisimosti ot dvizheniya nablyudatelya.
No dazhe v vashej strane ni odin nablyudatel' ne mozhet videt' sledstvie ran'she,
chem prichinu. Vam zhe nikogda ne sluchalos' poluchat' telegrammu do togo, kak ta
byla otpravlena, ved' verno? Ne sluchalos' i pit' do togo, kak butylku
otkuporili. Naskol'ko ya vas ponimayu, vy polagaete, chto iz-za dvizheniya poezda
my, passazhiry, nablyudali vystrel gorazdo _pozzhe_, chem ego sledstvie,
poskol'ku, vyskochiv iz vagona totchas zhe posle ekstrennoj ostanovki poezda,
my uvideli nachal'nika stancii lezhashchim na zemle, no eshche ne videli samogo
vystrela. YA znayu, chto v policii vas uchat verit' tol'ko tomu, chto napisano v
vashih instrukciyah. Vzglyanite v nih i vy, veroyatno, otyshchite chto-nibud'
podhodyashchee k sluchayu.
Ton professora proizvel neizgladimoe vpechatlenie na polismena i,
vytashchiv karmannyj svod instrukcij, on prinyalsya medlenno, stranica za
stranicej izuchat' ih. Vskore po ego shirokoj krasnoj fizionomii razlilas'
ulybka oblegcheniya.
- Vot, - skazal on, - razdel 37, chast' 12, paragraf e: "V kachestve
absolyutno nadezhnogo alibi sleduet schitat' lyuboe avtoritetnoe dokazatel'stvo
togo, chto iz lyuboj dvizhushchejsya sistemy otscheta v moment soversheniya
prestupleniya ili v techenie intervala vremeni +-cd (gde s - skorost' sveta, a
d - rasstoyanie ot mesta prestupleniya) podozrevaemogo videli v drugom meste".
- Vy svobodny, moj milyj, - obratilsya polismen k nosil'shchiku i dobavil,
povernuvshis' k professoru:
- Ochen' priznatelen vam, ser, chto vy izbavili menya ot nepriyatnostej s
policejskim upravleniem. YA v policii sluzhu nedavno i eshche ne vyuchil nazubok
vse pravila. No mne vse ravno neobhodimo dolozhit' ob ubijstve. I polismen
pospeshil k telefonnoj budke. CHerez minutu on zakrichal na ves' perron:
- Vse v poryadke! Oni pojmali nastoyashchego ubijcu, kogda tot bezhal so
stancii. Eshche raz blagodaryu vas, ser!
- Dolzhno byt', ya neprohodimo glup, - zametil mister Tompkins, kogda
poezd snova tronulsya, - no chto oznachaet vsya eta nerazberiha s
odnovremennost'yu? Imeet li odnovremennost' voobshche kakoj-nibud' smysl v etoj
strane?
- Imeet, - glasil otvet professora, - no lish' v opredelennoj stepeni,
inache ya ne smog by pomoch' bednyage-nosil'shchiku. Delo v tom, chto esli
sushchestvuet estestvennyj predel skorosti dlya dvizheniya lyubogo tela ili
rasprostraneniya lyubogo signala, to odnovremennost' v obychnom smysle etogo
slova utrachivaet smysl. Vam, veroyatno, budet legche ponyat' sut' dela na
sleduyushchem primere. Predpolozhim, chto u vas est' drug, zhivushchij v dalekom
gorode, s kotorym vy perepisyvaetes', i pochtovyj poezd, kotoryj otpravlyaetsya
raz v sutki, - samoe bystroe sredstvo soobshcheniya. Predpolozhim teper', chto
kakoe-to proisshestvie sluchilos' s vami v voskresen'e i vy uznali, chto
analogichnoe proisshestvie dolzhno proizojti s vashim drugom. YAsno, chto vy ne
mozhete uvedomit' ego ob etom ran'she vtornika. S drugoj storony, esli by on
znal zaranee o tom, chto proizojdet s vami, to poslednij den', kogda on mog
predupredit' vas o gryadushchem sobytii, byl chetverg na proshloj nedele. Takim
obrazom, v techenie shesti dnej - s chetverga na proshloj nedele do vtornika na
budushchej nedele - vash drug ne sposoben ni povliyat' na vashu sud'bu v
voskresen'e, ni uznat' o tom, chto s vami proizoshlo. S tochki zreniya
prichinnosti on iz座at iz obshcheniya s vami, ili, tak skazat', ekskommunicirovan.
- A chto esli emu poslat' telegrammu? - predlozhil mister Tompkins.
- No ved' ya predpolozhil, chto skorost' pochtovogo poezda - maksimal'no
vozmozhnaya. Primerno tak i obstoit delo v etoj strane. U nas na rodine
maksimal'noj skorost'yu yavlyaetsya skorost' sveta, i vy ne mozhete poslat'
signal, kotoroj rasprostranyalsya by bystree, chem radiosignal.
- Pust' tak, - soglasilsya mister Tompkins, - no dazhe esli nichto ne
mozhet prevzojti skorost' pochtovogo poezda, ya vse ravno ne ponimayu, kakoe eto
imeet otnoshenie k odnovremennosti. Moj drug i ya po-prezhnemu obedaem po
voskresen'yam v odno i to zhe vremya. Razve ne tak?
- Net, ne tak. Vashe utverzhdenie voobshche ne imelo by smysla: odin
nablyudatel' soglasilsya by s tem, chto vy s priyatelem obedaete odnovremenno, a
drugie nablyudateli, proizvodivshie svoi nablyudeniya iz drugih poezdov,
utverzhdali by, chto vy obedaete po voskresen'yam v to samoe vremya, kogda vash
drug zavtrakaet po pyatnicam ili uzhinaet po vtornikam. No nikto ne mozhet
nablyudat' vas i vashego druga za odnovremennoj trapezoj, esli vas razdelyaet
vremennoj interval bolee treh dnej.
- No kak eto mozhet byt'? - voskliknul nedoverchivo mister Tompkins.
- Proishodit vse eto tochno tak, kak vy, vozmozhno, uyasnili sebe iz moih
lekcij. Verhnij predel skorosti dolzhen ostavat'sya odnim i tem zhe pri
nablyudenii iz razlichnyh dvizhushchihsya sistem otscheta. Prinyav takoe
predpolozhenie, my s neobhodimost'yu prihodim k zaklyucheniyu o tom, chto...
Tut razgovor, k sozhaleniyu, prervalsya, tak kak poezd pribyl na tu
stanciyu, gde misteru Tompkinsu nuzhno bylo shodit'.
Kogda mister Tompkins spustilsya k zavtraku na dlinnuyu zasteklennuyu
verandu otelya na sleduyushchee utro posle svoego pribytiya na poberezh'e, ego
ozhidal priyatnyj syurpriz: na protivopolozhnom konce stola protiv nego vossedal
staryj professor s krasivoj molodoj devushkoj, kotoraya ozhivlenno chto-to
govorila emu, chasto poglyadyvaya v tu storonu, gde sidel mister Tompkins.
- Dolzhno byt', ya sovershil bol'shuyu glupost', kogda zasnul v poezde, -
podumal mister Tompkins, serdyas' na sebya vse bol'she i bol'she, - a professor
vse eshche pomnit tot glupyj vopros, kotoryj ya zadal emu o molodeyushchih
passazhirah. No po krajnej mere eto pozvolyaet mne prodolzhit' znakomstvo s
professorom i rassprosit' ego o tom, chto mne po-prezhnemu neponyatno.
Dazhe samomu sebe mister Tompkins ne hotel priznat'sya, chto dumaet ne
tol'ko o professore, no i o ego horoshen'koj sputnice.
- Da, da, konechno, ya pomnyu, chto videl vas na svoih lekciyah, - skazal
professor, kogda oni vyhodili iz obedennogo zala. - Poznakom'tes', eto moya
doch' Mod. Ona zanimaetsya zhivopis'yu.
- Rad poznakomit'sya s vami, miss Mod, - otvetil mister Tompkins i
podumal, chto nikogda ne slyshal bolee krasivogo imeni. - Dumayu, chto zdeshnie
krasoty dadut vam nemalo materiala dlya vashih etyudov.
- Mod nepremenno pokazhet ih vam kogda-nibud', - poobeshchal professor. - A
sejchas skazhite mne luchshe, mnogo li vy pocherpnuli iz moej lekcii?
- O da, ochen' mnogo! Bolee togo, ya na sebe prochuvstvoval vse eti
relyativistskie sokrashcheniya material'nyh ob容ktov i sumasshedshee povedenie
chasov, kogda pobyval v gorode, gde skorost' sveta sostavlyala tol'ko
kilometrov desyat' v chas.
- ZHal', chto vy propustili moyu sleduyushchuyu lekciyu o krivizne prostranstva
i ee svyazi s silami n'yutonovskoj gravitacii, - zadumchivo proiznes professor.
- No zdes', na poberezh'e, u nas hvatit vremeni, i ya nadeyus' ob座asnit' vam
vse eto. Naprimer, ponimaete li vy, v chem raznica mezhdu polozhitel'noj i
otricatel'noj kriviznoj prostranstva?
- Papochka, - vmeshalas' miss Mod, kaprizno naduv guby, - esli vy
sobiraetes' snova besedovat' o fizike, to ya luchshe zajmus' etyudami.
- Horosho, devochka, idi, - soglasilsya professor, opuskayas' v legkoe
kreslo. - YA vizhu, chto vy molodoj chelovek, ne ochen' svedushchi v matematike, no
dumayu, chto udastsya ob座asnit' vam vse ochen' prosto. Dlya bol'shej naglyadnosti ya
budu govorit' o poverhnosti. Predstav'te sebe, chto mister SHell (vy znaete, o
kom ya govoryu, - eto tot samyj gospodin, kotoryj vladeet benzozapravochnymi
stanciyami "SHell Ojl") reshil kak-to raz prosledit' za tem, chtoby ego
zapravochnye stancii byli ravnomerno raspredeleny po territorii kakoj-nibud'
strany, naprimer, Ameriki. Dlya etogo mister SHell otdal pravleniyu svoej
firmy, raspolozhennomu gde-to v centre strany (esli ya ne oshibayus', mnogie
sklonny dumat', chto serdce Ameriki nahoditsya v Kanzas-Siti), rasporyazhenie
soschitat' chislo stancij na rasstoyanii sto, dvesti, trista i t. d. mil' ot
centra. So shkol'noj skam'i mister SHell vynes vospominaniya o tom, chto ploshchad'
kruga proporcional'na kvadratu ego radiusa, i ozhidaet, chto v sluchae
ravnomernogo raspredeleniya zapravochnyh stancij chislo ih v rezul'tate
podschetov budet vozrastat', kak posledovatel'nost' chisel 1; 4; 9; 16 i t.d.
Kogda v pravlenie "SHell Ojl" stali postupat' otchety, glava firmy k svoemu
velikomu udivleniyu obnaruzhil, chto chislo stancij vozrastaet gorazdo
medlennee, naprimer, kak chisla, obrazuyushchie posledovatel'nost' 1; 3,8; 8,5;
15,0 i t.d.
 - CHto za d'yavol'shchina, - voskliknul mister SHell, - moi upravlyayushchie v
Amerike nichego ne smyslyat v svoem dele! Nu skazhite na milost', zachem im
ponadobilos' sosredotachivat' zapravochnye stancii v okrestnostyah Kanzas-Siti?
Prav li mister SHell v svoem zaklyuchenii?
- V samom dele, prav li on? - povtoril mister Tompkins, mysli kotorogo
gde-to vitali.
- Mister SHell gluboko zabluzhdaetsya, - mrachno izrek professor. - On
upustil iz vidu, chto poverhnost' Zemli ne ploskaya, a sfericheskaya, a na sfere
ploshchad', zaklyuchennaya vnutri kruga dannogo radiusa, rastet medlennee, chem na
ploskosti. Mozhete vy predstavit' sebe eto naglyadno? Net? Togda voz'mite
globus i ubedites' sami v tom, chto ya prav. Naprimer, esli vy nahodites' na
Severnom polyuse, to okruzhnost' radiusom v polovinu meridiana est' ne chto
inoe, kak ekvator, a zaklyuchennaya vnutri nee ploshchad' poverhnosti Zemli est'
ploshchad' severnogo polushariya. S uvelicheniem radiusa ploshchad' na poverhnosti
sfery vozrastaet tol'ko vdvoe, a ne vchetvero, kak bylo by na ploskosti.
Teper', nadeyus', yasno?
- O, da, - kivnul mister Tompkins, delaya vid, budto on vnimatel'no
sledit za ob座asneniyami. - A chto takoe polozhitel'naya ili otricatel'naya
krivizna?
- U sfery krivizna schitaetsya polozhitel'noj. Kak vy videli na primere
zemnogo shara, polozhitel'naya krivizna sootvetstvuet konechnoj poverhnosti,
imeyushchej konechnuyu ploshchad'. Primerom poverhnosti s otricatel'noj kriviznoj
mozhet sluzhit' sedlo.
- Sedlo? - peresprosil mister Tompkins.
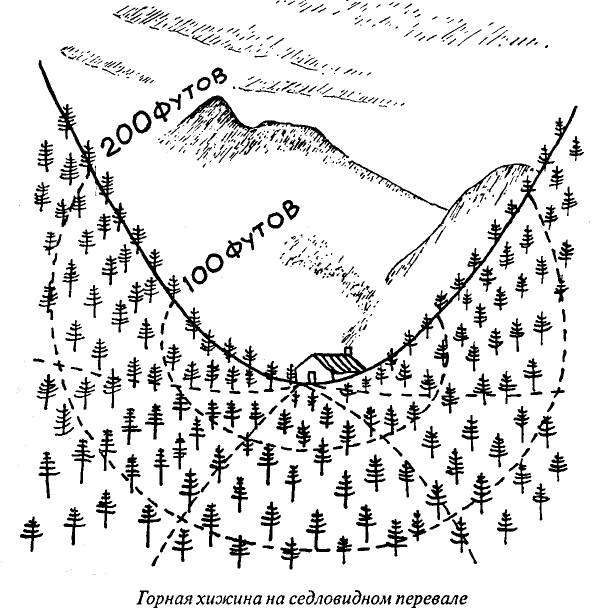
- Da, sedlo, ili na poverhnosti Zemli sedloobraznyj pereval mezhdu dvumya
gornymi vershinami. Predpolozhim, chto nekij botanik obitaet v gornoj hizhine,
raspolozhennoj na takom sedlovidnom perevale, i zanimaetsya izucheniem
plotnosti sosen, rastushchih vokrug ego zhilishcha. Podschitav chislo sosen, rastushchih
ne dalee sta, dvuhsot, trehsot i t. d. futov ot hizhiny, on obnaruzhit, chto
chislo sosen vozrastaet bystree, chem kvadrat rasstoyaniya, poskol'ku na
sedlovidnoj poverhnosti ploshchad', zaklyuchennaya vnutri dannogo radiusa, rastet
bystree, chem na ploskosti. O takih poverhnostyah govoryat, chto oni obladayut
otricatel'noj kriviznoj. Esli vy popytaetes', rastyanuv, nalozhit' sedlovidnuyu
poverhnost' na ploskost', to vam pridetsya sdelat' skladki. Esli zhe vy
zadumaete nalozhit' na ploskost' sfericheskuyu poverhnost', to vam pridetsya
gde-to prodelat' v nej dyrochku.
- Kazhetsya, ya nachinayu ponimat', - zadumchivo proiznes mister Tompkins. -
Vy hotite skazat', chto sedlovidnaya poverhnost' beskonechnaya, hotya i
iskrivlennaya.
- Vot imenno! - odobritel'no kivnul professor. - Sedlovidnaya
poverhnost' prostiraetsya vo vse storony do beskonechnosti i nigde ne
zamykaetsya. Razumeetsya, v moem primere s sedlovidnym perevalom poverhnost'
perestaet byt' poverhnost'yu otricatel'noj krivizny, kak tol'ko vy
spuskaetes' s gor, i perehodit v iskrivlennuyu poverhnost' zemnogo shara s
polozhitel'noj kriviznoj. No, razumeetsya, nichto ne meshaet vam voobrazit'
poverhnost', sohranyayushchuyu povsyudu otricatel'nuyu kriviznu.
- No kakoe otnoshenie imeet vse eto k iskrivlennomu trehmernomu
prostranstvu?
- Samoe neposredstvennoe. Predstav'te sebe, chto kakie-to vashi ob容kty
ravnomerno raspredeleny po vsemu prostranstvu. Pod ravnomernym ya ponimayu
takoe raspredelenie, pri kotorom rasstoyanie mezhdu lyubymi sosednimi ob容ktami
vsegda odno i to zhe. Predpolozhim, chto vy podschityvaete chislo ob容ktov,
raspolozhennyh ne dalee togo ili inogo rasstoyaniya ot vas. Esli eto chislo
rastet kak kvadrat rasstoyaniya, to prostranstvo ploskoe. Esli zhe chislo
ob容ktov rastet medlennee ili bystree, to prostranstvo obladaet
sootvetstvenno polozhitel'noj ili otricatel'noj kriviznoj.
- CHto za d'yavol'shchina, - voskliknul mister SHell, - moi upravlyayushchie v
Amerike nichego ne smyslyat v svoem dele! Nu skazhite na milost', zachem im
ponadobilos' sosredotachivat' zapravochnye stancii v okrestnostyah Kanzas-Siti?
Prav li mister SHell v svoem zaklyuchenii?
- V samom dele, prav li on? - povtoril mister Tompkins, mysli kotorogo
gde-to vitali.
- Mister SHell gluboko zabluzhdaetsya, - mrachno izrek professor. - On
upustil iz vidu, chto poverhnost' Zemli ne ploskaya, a sfericheskaya, a na sfere
ploshchad', zaklyuchennaya vnutri kruga dannogo radiusa, rastet medlennee, chem na
ploskosti. Mozhete vy predstavit' sebe eto naglyadno? Net? Togda voz'mite
globus i ubedites' sami v tom, chto ya prav. Naprimer, esli vy nahodites' na
Severnom polyuse, to okruzhnost' radiusom v polovinu meridiana est' ne chto
inoe, kak ekvator, a zaklyuchennaya vnutri nee ploshchad' poverhnosti Zemli est'
ploshchad' severnogo polushariya. S uvelicheniem radiusa ploshchad' na poverhnosti
sfery vozrastaet tol'ko vdvoe, a ne vchetvero, kak bylo by na ploskosti.
Teper', nadeyus', yasno?
- O, da, - kivnul mister Tompkins, delaya vid, budto on vnimatel'no
sledit za ob座asneniyami. - A chto takoe polozhitel'naya ili otricatel'naya
krivizna?
- U sfery krivizna schitaetsya polozhitel'noj. Kak vy videli na primere
zemnogo shara, polozhitel'naya krivizna sootvetstvuet konechnoj poverhnosti,
imeyushchej konechnuyu ploshchad'. Primerom poverhnosti s otricatel'noj kriviznoj
mozhet sluzhit' sedlo.
- Sedlo? - peresprosil mister Tompkins.
- Da, sedlo, ili na poverhnosti Zemli sedloobraznyj pereval mezhdu dvumya
gornymi vershinami. Predpolozhim, chto nekij botanik obitaet v gornoj hizhine,
raspolozhennoj na takom sedlovidnom perevale, i zanimaetsya izucheniem
plotnosti sosen, rastushchih vokrug ego zhilishcha. Podschitav chislo sosen, rastushchih
ne dalee sta, dvuhsot, trehsot i t. d. futov ot hizhiny, on obnaruzhit, chto
chislo sosen vozrastaet bystree, chem kvadrat rasstoyaniya, poskol'ku na
sedlovidnoj poverhnosti ploshchad', zaklyuchennaya vnutri dannogo radiusa, rastet
bystree, chem na ploskosti. O takih poverhnostyah govoryat, chto oni obladayut
otricatel'noj kriviznoj. Esli vy popytaetes', rastyanuv, nalozhit' sedlovidnuyu
poverhnost' na ploskost', to vam pridetsya sdelat' skladki. Esli zhe vy
zadumaete nalozhit' na ploskost' sfericheskuyu poverhnost', to vam pridetsya
gde-to prodelat' v nej dyrochku.
- Kazhetsya, ya nachinayu ponimat', - zadumchivo proiznes mister Tompkins. -
Vy hotite skazat', chto sedlovidnaya poverhnost' beskonechnaya, hotya i
iskrivlennaya.
- Vot imenno! - odobritel'no kivnul professor. - Sedlovidnaya
poverhnost' prostiraetsya vo vse storony do beskonechnosti i nigde ne
zamykaetsya. Razumeetsya, v moem primere s sedlovidnym perevalom poverhnost'
perestaet byt' poverhnost'yu otricatel'noj krivizny, kak tol'ko vy
spuskaetes' s gor, i perehodit v iskrivlennuyu poverhnost' zemnogo shara s
polozhitel'noj kriviznoj. No, razumeetsya, nichto ne meshaet vam voobrazit'
poverhnost', sohranyayushchuyu povsyudu otricatel'nuyu kriviznu.
- No kakoe otnoshenie imeet vse eto k iskrivlennomu trehmernomu
prostranstvu?
- Samoe neposredstvennoe. Predstav'te sebe, chto kakie-to vashi ob容kty
ravnomerno raspredeleny po vsemu prostranstvu. Pod ravnomernym ya ponimayu
takoe raspredelenie, pri kotorom rasstoyanie mezhdu lyubymi sosednimi ob容ktami
vsegda odno i to zhe. Predpolozhim, chto vy podschityvaete chislo ob容ktov,
raspolozhennyh ne dalee togo ili inogo rasstoyaniya ot vas. Esli eto chislo
rastet kak kvadrat rasstoyaniya, to prostranstvo ploskoe. Esli zhe chislo
ob容ktov rastet medlennee ili bystree, to prostranstvo obladaet
sootvetstvenno polozhitel'noj ili otricatel'noj kriviznoj.
 - Znachit, v sluchae prostranstva polozhitel'noj krivizny ob容m,
zaklyuchennyj v predelah dannogo rasstoyaniya, men'she, a v sluchae prostranstva
otricatel'noj krivizny - bol'she, chem v sluchae ploskogo prostranstva? - s
udivleniem sprosil mister Tompkins.
- Vot imenno! - ulybnulsya professor. - YA vizhu, chto teper' vy ponyali
menya pravil'no. CHtoby opredelit' znak krivizny toj ogromnoj Vselennoj, v
kotoroj my zhivem, neobhodimo lish' proizvodit' takie podschety udalennyh
ob容ktov. Bol'shie tumannosti, o kotoryh vy, vozmozhno, slyshali, rasseyany
ravnomerno v kosmicheskom prostranstve, i ih mozhno nablyudat' vplot' do
rasstoyanij v neskol'ko millionov svetovyh let. Dlya issledovaniya krivizny
Vselennoj eto ochen' udobnye ob容kty.
- I poluchaetsya, chto nasha Vselennaya konechna i zamknuta?
- Vidite li, - otvetil professor, - v dejstvitel'nosti eta problema vse
eshche ne reshena. V svoih rabotah po kosmologii |jnshtejn utverzhdal, chto nasha
Vselennaya imeet konechnye razmery, zamknuta i ne izmenyaetsya vo vremeni.
Odnako v bolee pozdnej rabote russkogo matematika Al. Fridmana bylo
pokazano, chto fundamental'nye uravneniya |jnshtejna dopuskayut takuyu
vozmozhnost', kak rasshirenie ili szhatie Vselennoj na bolee pozdnem etape
razvitiya. |to matematicheskoe zaklyuchenie bylo podtverzhdeno amerikanskim
astronomom |. Habblom, kotoryj, ispol'zuya stodyujmovyj teleskop observatorii
Maunt Vilson, obnaruzhil, chto galaktiki razletayutsya, t.e. nasha Vselennaya
rasshiryaetsya. Sushchestvuet, odnako, vse eshche nereshennaya problema otnositel'no
togo, budet li eto rasshirenie prodolzhat'sya neogranichenno ili radius
Vselennoj dostignet svoego maksimal'nogo znacheniya, posle chego v otdalennom
budushchem rasshirenie smenitsya szhatiem. Otvet na etot vopros mogut dat' tol'ko
bolee podrobnye astronomicheskie nablyudeniya.
Poka professor govoril, vokrug stali proishodit' ves'ma neobychnye
izmeneniya: odin konec koridora szhalsya i stal krohotnym, sdaviv vsyu stoyavshuyu
tam mebel', zato drugoj konec rasshirilsya i prodolzhal uvelichivat'sya v
razmerah, hotya uzhe sejchas, kak pokazalos' misteru Tompkinsu, on mog vmestit'
vsyu Vselennuyu. Uzhasnaya mysl' proneslas' v golove mistera Tompkinsa: chto esli
kusochek prostranstva s plyazhem, gde miss Mod risovala svoi etyudy, otorvalsya
ot osnovnoj chasti Vselennoj? - Togda, - podumal mister Tompkins, - ya nikogda
ne uvizhu ee snova!
Mister Tompkins brosilsya k vyhodu. Poslednee, chto on uslyshal, byl golos
professora, krichavshego emu vsled:
- Ostorozhnee! Kvantovaya postoyannaya takzhe shodit s uma!
Kogda mister Tompkins dostig plyazha, emu pokazalos', chto on perepolnen.
Tysyachi devushek nosilis' po vsem napravleniyam, sozdavaya dikuyu nerazberihu.
- Kak zhe ya smogu najti moyu Mod v etoj tolpe? - rasteryanno podumal
mister Tompkins. No priglyadevshis', on zametil, chto vse devushki vyglyadeli
tochno tak zhe, kak doch' professora, i ponyal, chto eto neobychajnoe shodstvo
bylo igroj principa neopredelennosti. V sleduyushchij moment volna anomal'no
bol'shoj kvantovoj postoyannoj proshla, i pered misterom Tompkinsom na plyazhe
okazalas' miss Mod s ispugannym vyrazheniem v glazah.
- Ah, eto vy! - vzdohnula ona s oblegcheniem. - A mne pokazalos', chto
ogromnaya tolpa zatopchet menya. Dolzhno byt', ya peregrelas' na solnce i eto mne
pomereshchilos'. Podozhdite, pozhalujsta, menya zdes', ya tol'ko na minutku sbegayu
v otel' za shlyapoj.
- Net-net, my ne dolzhny rasstavat'sya, - zaprotestoval mister Tompkins.
- Mne kazhetsya, chto skorost' sveta takzhe menyaetsya. Vernuvshis' so shlyapoj, vy
mozhete zastat' menya dryahlym starikom.
- Ne govorite chepuhi, - vozrazila devushka, no vzyala mistera Tompkinsa
pod ruku. A na polputi k otelyu novaya volna neopredelennosti nakryla ih, i
mister Tompkins i ego sputnica okazalis' razmazannymi po vsemu beregu.
Odnovremenno s okrestnyh holmov nachala rasprostranyat'sya skladka
prostranstva, prichudlivo iskazhaya ochertaniya pribrezhnyh skal i rybackih
domikov. Luchi Solnca, otrazhennye ot intensivnogo gravitacionnogo polya,
polnost'yu ischezli za gorizontom, i mister Tompkins pogruzilsya v kromeshnuyu
t'mu.
Proshla celaya vechnost', prezhde chem stol' milyj ego serdcu golos ne
privel ego v chuvstvo.
- O, ya vizhu moj papochka sovsem usypil vas svoimi razgovorami o fizike,
- proshchebetala miss Mod. - Ne hotite li vy pojti so mnoj poplavat'? Voda
segodnya prosto velikolepnaya.
Mister Tompkins podprygnul so svoego legkogo kresla, kak na pruzhinah.
- Tak eto byl tol'ko son, - podumal on, kogda oni spuskalis' k plyazhu. -
Ili son tol'ko teper' nachinaetsya?
�Glava 4�
Lekciya professora ob iskrivlennom prostranstve, gravitacii i vselennoj
Ledi i dzhentl'meny!
Segodnya ya namerevayus' rassmotret' problemu iskrivlennogo prostranstva i
ee svyaz' s yavleniyami gravitacii. Ne somnevayus', chto kazhdyj iz vas bez truda
mozhet predstavit' sebe iskrivlennuyu liniyu (krivuyu) ili iskrivlennuyu
poverhnost', no pri upominanii ob iskrivlennom trehmernom prostranstve vashi
lica vytyagivayutsya i vy sklonny dumat', chto eto nechto ves'ma neobychnoe i
pochti sverh容stestvennoe. Pochemu iskrivlennoe prostranstvo vyzyvaet vseobshchij
"uzhas"? Dejstvitel'no li ponyatie iskrivlennogo prostranstva trudnee dlya
ponimaniya, chem ponyatie iskrivlennoj poverhnosti? Mnogie iz vas, porazmysliv
nemnogo nad etimi voprosami, veroyatno, skazhut, chto predstavit' iskrivlennoe
trehmernoe prostranstvo trudnee po odnoj-edinstvennoj prichine: my ne mozhem
vzglyanut' na prostranstvo "so storony", kak my smotrim na iskrivlennuyu
poverhnost' shara, ili, esli obratit'sya k drugomu primeru, na takuyu osobym
obrazom izognutuyu poverhnost', kak sedlo. No te, kto tak govoryat, obrekayut
sebya na neznanie strogo matematicheskogo smysla krivizny, sushchestvenno
otlichayushchegosya ot obshcheupotreblyaemogo znacheniya etogo slova. My, matematiki,
nazyvaem poverhnost' iskrivlennoj, esli svojstva geometricheskih figur,
nacherchennyh na nej, otlichny ot svojstv figur na ploskosti, i izmeryaem
kriviznu otkloneniem ot klassicheskih pravil Evklida. Esli vy nachertite
treugol'nik na ploskom liste bumagi, to, kak izvestno iz elementarnoj
geometrii, summa ego vnutrennih uglov ravna dvum pryamym. Vy mozhete izognut'
etot list bumagi, pridav emu formu cilindra, konusa ili kakoj-nibud' bolee
slozhnoj figury, no summa uglov nacherchennogo na nem treugol'nika neizmenno
budet ostavat'sya ravnoj dvum pryamym uglam.
Geometriya poverhnosti ne menyaetsya pri etih deformaciyah i s tochki zreniya
"vnutrennej" krivizny poluchayushchiesya poverhnosti (iskrivlennye v obychnom
smysle) takie zhe ploskie, kak obychnaya ploskost'. No vy ne mozhete nalozhit'
list bumagi, ne rastyagivaya ego, na poverhnost' sfery ili sedla, a esli vy
nachertite treugol'nik na poverhnosti sfery (t.e. postroite sfericheskij
treugol'nik), to prostye teoremy evklidovoj geometrii vypolnyat'sya ne budut.
Naprimer, treugol'nik, obrazovannyj severnymi polovinami meridianov i
zaklyuchennoj mezhdu nimi dugoj ekvatora, imeet dva pryamyh ugla pri osnovanii i
proizvol'nyj ugol pri vershine.
Vozmozhno, vy udivites', kogda uznaete, chto na sedlovidnoj poverhnosti
summa uglov treugol'nika, naoborot, vsegda men'she dvuh pryamyh.
Takim obrazom, _chtoby opredelit' kriviznu poverhnosti, neobhodimo
izuchit' geometriyu na etoj poverhnosti_. Vzglyad zhe izvne na poverhnost' chasto
byvaet oshibochnym. Glyadya na poverhnost' izvne, vy skoree vsego otnesli by
poverhnost' cilindra k tomu zhe klassu, chto i poverhnost' obruchal'nogo
kol'ca. Mezhdu tem pervaya poverhnost' ploskaya, a vtoraya neizlechimo
iskrivlena. Kak tol'ko vy privyknite k etomu novomu strogomu ponyatiyu
krivizny, u vas ne budet bolee nikakih trudnostej v ponimanii togo, chto
imeyut v vidu fiziki, rassuzhdaya o tom, iskrivleno ili plosko prostranstvo, v
kotorom my zhivem. Problema zaklyuchaetsya tol'ko v vyyasnenii togo, podchinyayutsya
ili ne podchinyayutsya obychnym pravilam evklidovoj geometrii geometricheskie
figury, postroennye v fizicheskom prostranstve.
No poskol'ku my govorim o real'nom fizicheskom prostranstve, nam
neobhodimo prezhde vsego dat' _fizicheskoe opredelenie terminov, ispol'zuemyh
v geometrii_, i, v chastnosti, ukazat', chto my ponimaem pod pryamymi, iz
kotoryh postroeny figury.
- Znachit, v sluchae prostranstva polozhitel'noj krivizny ob容m,
zaklyuchennyj v predelah dannogo rasstoyaniya, men'she, a v sluchae prostranstva
otricatel'noj krivizny - bol'she, chem v sluchae ploskogo prostranstva? - s
udivleniem sprosil mister Tompkins.
- Vot imenno! - ulybnulsya professor. - YA vizhu, chto teper' vy ponyali
menya pravil'no. CHtoby opredelit' znak krivizny toj ogromnoj Vselennoj, v
kotoroj my zhivem, neobhodimo lish' proizvodit' takie podschety udalennyh
ob容ktov. Bol'shie tumannosti, o kotoryh vy, vozmozhno, slyshali, rasseyany
ravnomerno v kosmicheskom prostranstve, i ih mozhno nablyudat' vplot' do
rasstoyanij v neskol'ko millionov svetovyh let. Dlya issledovaniya krivizny
Vselennoj eto ochen' udobnye ob容kty.
- I poluchaetsya, chto nasha Vselennaya konechna i zamknuta?
- Vidite li, - otvetil professor, - v dejstvitel'nosti eta problema vse
eshche ne reshena. V svoih rabotah po kosmologii |jnshtejn utverzhdal, chto nasha
Vselennaya imeet konechnye razmery, zamknuta i ne izmenyaetsya vo vremeni.
Odnako v bolee pozdnej rabote russkogo matematika Al. Fridmana bylo
pokazano, chto fundamental'nye uravneniya |jnshtejna dopuskayut takuyu
vozmozhnost', kak rasshirenie ili szhatie Vselennoj na bolee pozdnem etape
razvitiya. |to matematicheskoe zaklyuchenie bylo podtverzhdeno amerikanskim
astronomom |. Habblom, kotoryj, ispol'zuya stodyujmovyj teleskop observatorii
Maunt Vilson, obnaruzhil, chto galaktiki razletayutsya, t.e. nasha Vselennaya
rasshiryaetsya. Sushchestvuet, odnako, vse eshche nereshennaya problema otnositel'no
togo, budet li eto rasshirenie prodolzhat'sya neogranichenno ili radius
Vselennoj dostignet svoego maksimal'nogo znacheniya, posle chego v otdalennom
budushchem rasshirenie smenitsya szhatiem. Otvet na etot vopros mogut dat' tol'ko
bolee podrobnye astronomicheskie nablyudeniya.
Poka professor govoril, vokrug stali proishodit' ves'ma neobychnye
izmeneniya: odin konec koridora szhalsya i stal krohotnym, sdaviv vsyu stoyavshuyu
tam mebel', zato drugoj konec rasshirilsya i prodolzhal uvelichivat'sya v
razmerah, hotya uzhe sejchas, kak pokazalos' misteru Tompkinsu, on mog vmestit'
vsyu Vselennuyu. Uzhasnaya mysl' proneslas' v golove mistera Tompkinsa: chto esli
kusochek prostranstva s plyazhem, gde miss Mod risovala svoi etyudy, otorvalsya
ot osnovnoj chasti Vselennoj? - Togda, - podumal mister Tompkins, - ya nikogda
ne uvizhu ee snova!
Mister Tompkins brosilsya k vyhodu. Poslednee, chto on uslyshal, byl golos
professora, krichavshego emu vsled:
- Ostorozhnee! Kvantovaya postoyannaya takzhe shodit s uma!
Kogda mister Tompkins dostig plyazha, emu pokazalos', chto on perepolnen.
Tysyachi devushek nosilis' po vsem napravleniyam, sozdavaya dikuyu nerazberihu.
- Kak zhe ya smogu najti moyu Mod v etoj tolpe? - rasteryanno podumal
mister Tompkins. No priglyadevshis', on zametil, chto vse devushki vyglyadeli
tochno tak zhe, kak doch' professora, i ponyal, chto eto neobychajnoe shodstvo
bylo igroj principa neopredelennosti. V sleduyushchij moment volna anomal'no
bol'shoj kvantovoj postoyannoj proshla, i pered misterom Tompkinsom na plyazhe
okazalas' miss Mod s ispugannym vyrazheniem v glazah.
- Ah, eto vy! - vzdohnula ona s oblegcheniem. - A mne pokazalos', chto
ogromnaya tolpa zatopchet menya. Dolzhno byt', ya peregrelas' na solnce i eto mne
pomereshchilos'. Podozhdite, pozhalujsta, menya zdes', ya tol'ko na minutku sbegayu
v otel' za shlyapoj.
- Net-net, my ne dolzhny rasstavat'sya, - zaprotestoval mister Tompkins.
- Mne kazhetsya, chto skorost' sveta takzhe menyaetsya. Vernuvshis' so shlyapoj, vy
mozhete zastat' menya dryahlym starikom.
- Ne govorite chepuhi, - vozrazila devushka, no vzyala mistera Tompkinsa
pod ruku. A na polputi k otelyu novaya volna neopredelennosti nakryla ih, i
mister Tompkins i ego sputnica okazalis' razmazannymi po vsemu beregu.
Odnovremenno s okrestnyh holmov nachala rasprostranyat'sya skladka
prostranstva, prichudlivo iskazhaya ochertaniya pribrezhnyh skal i rybackih
domikov. Luchi Solnca, otrazhennye ot intensivnogo gravitacionnogo polya,
polnost'yu ischezli za gorizontom, i mister Tompkins pogruzilsya v kromeshnuyu
t'mu.
Proshla celaya vechnost', prezhde chem stol' milyj ego serdcu golos ne
privel ego v chuvstvo.
- O, ya vizhu moj papochka sovsem usypil vas svoimi razgovorami o fizike,
- proshchebetala miss Mod. - Ne hotite li vy pojti so mnoj poplavat'? Voda
segodnya prosto velikolepnaya.
Mister Tompkins podprygnul so svoego legkogo kresla, kak na pruzhinah.
- Tak eto byl tol'ko son, - podumal on, kogda oni spuskalis' k plyazhu. -
Ili son tol'ko teper' nachinaetsya?
�Glava 4�
Lekciya professora ob iskrivlennom prostranstve, gravitacii i vselennoj
Ledi i dzhentl'meny!
Segodnya ya namerevayus' rassmotret' problemu iskrivlennogo prostranstva i
ee svyaz' s yavleniyami gravitacii. Ne somnevayus', chto kazhdyj iz vas bez truda
mozhet predstavit' sebe iskrivlennuyu liniyu (krivuyu) ili iskrivlennuyu
poverhnost', no pri upominanii ob iskrivlennom trehmernom prostranstve vashi
lica vytyagivayutsya i vy sklonny dumat', chto eto nechto ves'ma neobychnoe i
pochti sverh容stestvennoe. Pochemu iskrivlennoe prostranstvo vyzyvaet vseobshchij
"uzhas"? Dejstvitel'no li ponyatie iskrivlennogo prostranstva trudnee dlya
ponimaniya, chem ponyatie iskrivlennoj poverhnosti? Mnogie iz vas, porazmysliv
nemnogo nad etimi voprosami, veroyatno, skazhut, chto predstavit' iskrivlennoe
trehmernoe prostranstvo trudnee po odnoj-edinstvennoj prichine: my ne mozhem
vzglyanut' na prostranstvo "so storony", kak my smotrim na iskrivlennuyu
poverhnost' shara, ili, esli obratit'sya k drugomu primeru, na takuyu osobym
obrazom izognutuyu poverhnost', kak sedlo. No te, kto tak govoryat, obrekayut
sebya na neznanie strogo matematicheskogo smysla krivizny, sushchestvenno
otlichayushchegosya ot obshcheupotreblyaemogo znacheniya etogo slova. My, matematiki,
nazyvaem poverhnost' iskrivlennoj, esli svojstva geometricheskih figur,
nacherchennyh na nej, otlichny ot svojstv figur na ploskosti, i izmeryaem
kriviznu otkloneniem ot klassicheskih pravil Evklida. Esli vy nachertite
treugol'nik na ploskom liste bumagi, to, kak izvestno iz elementarnoj
geometrii, summa ego vnutrennih uglov ravna dvum pryamym. Vy mozhete izognut'
etot list bumagi, pridav emu formu cilindra, konusa ili kakoj-nibud' bolee
slozhnoj figury, no summa uglov nacherchennogo na nem treugol'nika neizmenno
budet ostavat'sya ravnoj dvum pryamym uglam.
Geometriya poverhnosti ne menyaetsya pri etih deformaciyah i s tochki zreniya
"vnutrennej" krivizny poluchayushchiesya poverhnosti (iskrivlennye v obychnom
smysle) takie zhe ploskie, kak obychnaya ploskost'. No vy ne mozhete nalozhit'
list bumagi, ne rastyagivaya ego, na poverhnost' sfery ili sedla, a esli vy
nachertite treugol'nik na poverhnosti sfery (t.e. postroite sfericheskij
treugol'nik), to prostye teoremy evklidovoj geometrii vypolnyat'sya ne budut.
Naprimer, treugol'nik, obrazovannyj severnymi polovinami meridianov i
zaklyuchennoj mezhdu nimi dugoj ekvatora, imeet dva pryamyh ugla pri osnovanii i
proizvol'nyj ugol pri vershine.
Vozmozhno, vy udivites', kogda uznaete, chto na sedlovidnoj poverhnosti
summa uglov treugol'nika, naoborot, vsegda men'she dvuh pryamyh.
Takim obrazom, _chtoby opredelit' kriviznu poverhnosti, neobhodimo
izuchit' geometriyu na etoj poverhnosti_. Vzglyad zhe izvne na poverhnost' chasto
byvaet oshibochnym. Glyadya na poverhnost' izvne, vy skoree vsego otnesli by
poverhnost' cilindra k tomu zhe klassu, chto i poverhnost' obruchal'nogo
kol'ca. Mezhdu tem pervaya poverhnost' ploskaya, a vtoraya neizlechimo
iskrivlena. Kak tol'ko vy privyknite k etomu novomu strogomu ponyatiyu
krivizny, u vas ne budet bolee nikakih trudnostej v ponimanii togo, chto
imeyut v vidu fiziki, rassuzhdaya o tom, iskrivleno ili plosko prostranstvo, v
kotorom my zhivem. Problema zaklyuchaetsya tol'ko v vyyasnenii togo, podchinyayutsya
ili ne podchinyayutsya obychnym pravilam evklidovoj geometrii geometricheskie
figury, postroennye v fizicheskom prostranstve.
No poskol'ku my govorim o real'nom fizicheskom prostranstve, nam
neobhodimo prezhde vsego dat' _fizicheskoe opredelenie terminov, ispol'zuemyh
v geometrii_, i, v chastnosti, ukazat', chto my ponimaem pod pryamymi, iz
kotoryh postroeny figury.
 Dumayu, vse vy znaete, chto pryamuyu chashche vsego opredelyayut kak kratchajshee
rasstoyanie mezhdu dvumya tochkami. Pryamuyu mozhno postroit', libo natyanuv nit'
mezhdu dvumya tochkami, libo s pomoshch'yu kakogo-nibud' ekvivalentnogo, no bolee
slozhnogo processa, ustanoviv opytnym putem liniyu mezhdu dvumya dannymi
tochkami, vdol' kotoroj minimal'noe chislo raz ukladyvaetsya mernyj sterzhen'
dannoj dliny.
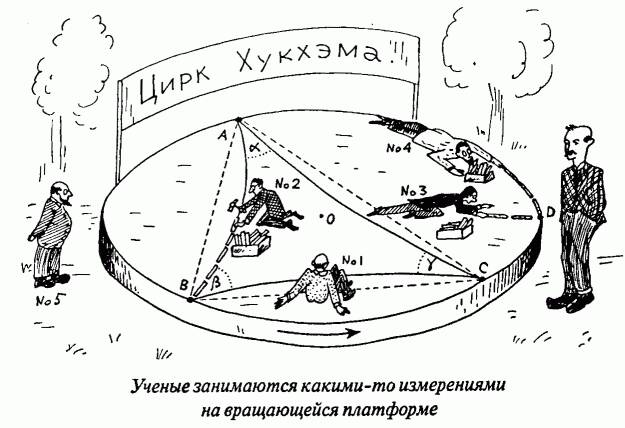
CHtoby pokazat', chto rezul'taty postroeniya pryamoj s pomoshch'yu takogo
metoda zavisyat ot fizicheskih uslovij, predstavim sebe bol'shuyu krugluyu
platformu, ravnomerno vrashchayushchuyusya vokrug svoej osi {Nazvanie "Cirk Hukhema"
voshodit k misteru Dzhonu Hukhemu, rabotavshemu hudozhnikom-illyustratorom v
izdatel'stve Kembridzhskogo universiteta. Nezadolgo do vyhoda v otstavku
mister Hukhem sozdal mnogie iz risunkov, ukrasivshih etu knigu.}, i pust'
eksperimentator |2 pytaetsya najti kratchajshee rasstoyanie mezhdu dvumya tochkami
na krayu platformy. U eksperimentatora imeetsya korobka s ogromnym chislom
sterzhnej, kazhdyj dlinoj 5 dyujmov, i on pytaetsya vylozhit' iz minimal'nogo
chisla etih sterzhnej liniyu, soedinyayushchuyu dve dannye tochki A i V. Esli by
platforma ne vrashchalas', to nash eksperimentator raspolozhil by sterzhni vdol'
shtrihovoj linii mezhdu tochkami A i V. No iz-za vrashcheniya platformy ego mernye
sterzhni preterpevayut relyativistskoe sokrashchenie, o kotorom ya rasskazal vam v
moej predydushchej lekcii, prichem te iz nih, kotorye raspolozheny blizhe k krayu
platformy (i, sledovatel'no, obladayut bol'shimi linejnymi skorostyami),
sokrashchayutsya sil'nee, chem sterzhni, raspolozhennye blizhe k centru. YAsno, chto
dlya togo chtoby kazhdyj sterzhen' pokryval kak mozhno bol'shee rasstoyanie,
sterzhni neobhodimo raspolagat' kak mozhno blizhe k centru. No poskol'ku oba
konca linii zakrepleny na krayu platformy, sdvigat' vse sterzhni ot serediny
linii slishkom blizko k centru nevygodno.
V rezul'tate nash fizik dostignet nekoego kompromissa mezhdu etimi dvumya
usloviyami, i _kratchajshee rasstoyanie budet v konce koncov predstavleno
krivoj, slegka vypukloj v storonu centra_.
Esli nash eksperimentator vmesto otdel'nyh sterzhnej natyanet mezhdu dvumya
dannymi tochkami A i V nit', to rezul'tat, kak netrudno ponyat', poluchitsya
prezhnim, poskol'ku kazhdyj otrezok niti preterpevaet takoe zhe relyativistskoe
sokrashchenie, kak otdel'nye sterzhni. YA hochu osobo podcherknut', chto
relyativistskaya deformaciya natyanutoj niti, proishodyashchaya, kogda platforma
nachinaet vrashchat'sya, ne imeet nichego obshchego s obychnymi effektami centrobezhnoj
sily. Relyativistskaya deformaciya ostaetsya neizmennoj, kak by sil'no ni byla
natyanuta nit', ne govorya uzhe o tom, chto obychnaya centrobezhnaya sila dejstvuet
v protivopolozhnom napravlenii.
Esli nablyudatel', nahodyashchijsya na platforme, vzdumaet proverit'
rezul'tat svoih postroenij, sravniv poluchennuyu "pryamuyu" s luchom sveta, to on
obnaruzhit, chto svet dejstvitel'no rasprostranyaetsya vdol' postroennoj im
linii. Razumeetsya, dlya nablyudatelej, stoyashchih u platformy, luch sveta voobshche
ne budet iskrivlen. Oni budut interpretirovat' rezul'taty dvizhushchegosya
nablyudatelya putem superpozicii, ili nalozheniya, vrashcheniya platformy i
pryamolinejnogo rasprostraneniya sveta. Oni skazhut vam, chto esli vy nanesete
carapinu na vrashchayushchuyusya grammofonnuyu plastinku, dvinuv rukoj po pryamoj, to
carapina na plastinke, konechno zhe, budet iskrivlennoj.
No dlya nablyudatelya, nahodyashchegosya na vrashchayushchejsya platforme, nazvanie
"pryamaya" dlya postroennoj im krivoj vpolne razumno: eta krivaya daet
_kratchajshee rasstoyanie_ i sovpadaet s _luchom sveta_ v sisteme otscheta nashego
nablyudatelya. Predpolozhim, chto on vybral na krayu platformy tri tochki i
soedinil ih pryamymi, postroiv tem samym treugol'nik. _Summa uglov v etom
treugol'nike men'she dvuh pryamyh_, iz chego nash nablyudatel' zaklyuchaet (i
sovershenno spravedlivo), chto prostranstvo vokrug nego iskrivleno.
Rassmotrim drugoj primer. Predpolozhim, chto dva drugih nablyudatelya na
platforme (|3 i |4) reshili ocenit' chislo pi, izmeryaya dlinu okruzhnosti
platformy i ee diametr. Na mernyj sterzhen' nablyudatelya |3 vrashchenie ne
vliyaet, poskol'ku dvizhenie sterzhnya vsegda perpendikulyarno ego dline. S
drugoj storony, mernyj sterzhen' nablyudatelya |4 vsegda budet sokrashchen, i dlya
dliny okruzhnosti platformy etot nablyudatel' poluchit bol'shee znachenie, chem v
sluchae nevrashchayushchejsya platformy. Delya rezul'tat, poluchennyj nablyudatelem 4,
na rezul'tat, poluchennyj nablyudatelem 3, my poluchim znachenie, prevyshayushchee
znachenie pi, obychno privodimoe v uchebnikah. |to takzhe yavlyaetsya sledstviem
krivizny prostranstva.
Vrashchenie vliyaet ne tol'ko na izmereniya dlin. CHasy, raspolozhennye na
krayu platformy, budut dvigat'sya s bol'shej skorost'yu i, kak bylo pokazano v
predydushchej lekcii, ih hod zamedlitsya po sravneniyu s hodom chasov,
ustanovlennyh v centre platformy.
Esli dva eksperimentatora (|4 i |5) sveryat chasy v centre platformy, a
zatem eksperimentator |5 na kakoe-to vremya otneset svoi chasy na kraj
platformy, to po vozvrashchenii v centr on obnaruzhit, chto ego chasy otstayut po
sravneniyu s chasami, vse vremya ostavavshimisya v centre platformy. Iz etogo
eksperimentator |5 sdelaet vyvod, chto v razlichnyh mestah platformy vse
fizicheskie processy idut s razlichnymi skorostyami. Predpolozhim teper', chto
nashi eksperimentatory ostanovilis' i nemnogo porazmyslili nad prichinoj
neobychnyh rezul'tatov, tol'ko chto poluchennyh imi v geometricheskih
izmereniyah. Predpolozhim takzhe, chto vrashchayushchayasya platforma zakryta so vseh
storon i predstavlyaet soboj vrashchayushchuyusya komnatu bez okon, chtoby
eksperimentatory ne mogli nablyudat' svoe dvizhenie otnositel'no okruzhayushchih
predmetov. Mogli by v etom sluchae eksperimentatory ob座asnit' vse poluchennye
rezul'taty chisto fizicheskimi usloviyami na platforme bez ucheta ee vrashcheniya
otnositel'no "tverdoj osnovy", na kotoroj ustanovlena platforma?
Glyadya na razlichiya mezhdu fizicheskimi usloviyami na platforme i na
"tverdoj osnove", posredstvom kotoryh mozhno bylo by ob座asnit' nablyudaemye
izmeneniya v geometrii, nashi eksperimentatory srazu zhe zametili by, chto
sushchestvuet kakaya-to novaya sila, kotoraya stremitsya otbrosit' vse tela ot
centra platformy k ee okruzhnosti. Vpolne estestvenno, chto oni pripisali by
nablyudaemye effekty dejstviyu etoj sily, utverzhdaya, naprimer, chto iz dvuh
chasov te budut idti medlennee, kotorye raspolozheny dal'she ot centra v
napravlenii novoj sily.
No dejstvitel'no li eta novaya sila nova, t. e. ne nablyudaema na
"tverdoj osnove"? Razve my ne nablyudaem, kak vse tela prityagivayutsya k centru
Zemli siloj, kotoraya poluchila nazvanie sily tyazhesti? Razumeetsya, v odnom
sluchae my imeem prityazhenie k okruzhnosti diska, v drugom - prityazhenie k
centru Zemli, no eto oznachaet tol'ko razlichie v raspredelenii sily.
Netrudno, odnako, privesti drugoj primer, kogda "novaya" sila, porozhdaemaya
neravnomernym dvizheniem sistemy otscheta, vyglyadit tochno tak zhe, kak sila
tyazhesti v etoj lekcionnoj auditorii.
Predpolozhim, chto kosmicheskij korabl', prednaznachennyj dlya mezhzvezdnyh
pereletov, svobodno letit gde-to v kosmicheskom prostranstve nastol'ko daleko
ot razlichnyh zvezd, chto vnutri korablya sila tyazhesti ne dejstvuet. Vse
predmety vnutri kosmicheskogo korablya i sami puteshestvuyushchie v nem
eksperimentatory nevesomy i svobodno plavayut v vozduhe primerno tak zhe, kak
Mishel' Ardan i ego sputniki vo vremya puteshestviya na Lunu v znamenitom romane
ZHyulya Verna.
No vot dvigateli vklyucheny i kosmicheskij korabl' prihodit v dvizhenie,
postepenno nabiraya skorost'. CHto proishodit vnutri nego? Netrudno videt',
chto poka kosmicheskij korabl' uskoryaetsya, vse predmety vnutri nego
obnaruzhivayut stremlenie dvigat'sya k polu, ili, chto to zhe, pol dvizhetsya
navstrechu etim predmetam. Naprimer, esli nash eksperimentator derzhit v ruke
yabloko i vypuskaet ego, to yabloko prodolzhaet dvigat'sya (otnositel'no
okruzhayushchih korabl' zvezd) s postoyannoj skorost'yu - toj samoj, s kotoroj
dvigalsya kosmicheskij korabl', kogda eksperimentator vypustil iz ruk yabloko.
No kosmicheskij korabl' uskoryaetsya. Sledovatel'no, pol kabiny, dvigayas' vse
bystree i bystree, v konce koncov dogonit yabloko i stuknet ego. S etogo
momenta yabloko ostanetsya v postoyannom kontakte s polom, buduchi prizhato k
polu postoyanno dejstvuyushchim uskoreniem.
No dlya eksperimentatora, nahodyashchegosya vnutri kosmicheskogo korablya, vse
vyglyadit inache: yabloko "padaet" s kakim-to uskoreniem i, udarivshis' ob pol,
ostaetsya lezhat' na polu, pridavlennoe k nemu sobstvennym vesom. Brosaya
razlichnye predmety, nash eksperiment
Dumayu, vse vy znaete, chto pryamuyu chashche vsego opredelyayut kak kratchajshee
rasstoyanie mezhdu dvumya tochkami. Pryamuyu mozhno postroit', libo natyanuv nit'
mezhdu dvumya tochkami, libo s pomoshch'yu kakogo-nibud' ekvivalentnogo, no bolee
slozhnogo processa, ustanoviv opytnym putem liniyu mezhdu dvumya dannymi
tochkami, vdol' kotoroj minimal'noe chislo raz ukladyvaetsya mernyj sterzhen'
dannoj dliny.
CHtoby pokazat', chto rezul'taty postroeniya pryamoj s pomoshch'yu takogo
metoda zavisyat ot fizicheskih uslovij, predstavim sebe bol'shuyu krugluyu
platformu, ravnomerno vrashchayushchuyusya vokrug svoej osi {Nazvanie "Cirk Hukhema"
voshodit k misteru Dzhonu Hukhemu, rabotavshemu hudozhnikom-illyustratorom v
izdatel'stve Kembridzhskogo universiteta. Nezadolgo do vyhoda v otstavku
mister Hukhem sozdal mnogie iz risunkov, ukrasivshih etu knigu.}, i pust'
eksperimentator |2 pytaetsya najti kratchajshee rasstoyanie mezhdu dvumya tochkami
na krayu platformy. U eksperimentatora imeetsya korobka s ogromnym chislom
sterzhnej, kazhdyj dlinoj 5 dyujmov, i on pytaetsya vylozhit' iz minimal'nogo
chisla etih sterzhnej liniyu, soedinyayushchuyu dve dannye tochki A i V. Esli by
platforma ne vrashchalas', to nash eksperimentator raspolozhil by sterzhni vdol'
shtrihovoj linii mezhdu tochkami A i V. No iz-za vrashcheniya platformy ego mernye
sterzhni preterpevayut relyativistskoe sokrashchenie, o kotorom ya rasskazal vam v
moej predydushchej lekcii, prichem te iz nih, kotorye raspolozheny blizhe k krayu
platformy (i, sledovatel'no, obladayut bol'shimi linejnymi skorostyami),
sokrashchayutsya sil'nee, chem sterzhni, raspolozhennye blizhe k centru. YAsno, chto
dlya togo chtoby kazhdyj sterzhen' pokryval kak mozhno bol'shee rasstoyanie,
sterzhni neobhodimo raspolagat' kak mozhno blizhe k centru. No poskol'ku oba
konca linii zakrepleny na krayu platformy, sdvigat' vse sterzhni ot serediny
linii slishkom blizko k centru nevygodno.
V rezul'tate nash fizik dostignet nekoego kompromissa mezhdu etimi dvumya
usloviyami, i _kratchajshee rasstoyanie budet v konce koncov predstavleno
krivoj, slegka vypukloj v storonu centra_.
Esli nash eksperimentator vmesto otdel'nyh sterzhnej natyanet mezhdu dvumya
dannymi tochkami A i V nit', to rezul'tat, kak netrudno ponyat', poluchitsya
prezhnim, poskol'ku kazhdyj otrezok niti preterpevaet takoe zhe relyativistskoe
sokrashchenie, kak otdel'nye sterzhni. YA hochu osobo podcherknut', chto
relyativistskaya deformaciya natyanutoj niti, proishodyashchaya, kogda platforma
nachinaet vrashchat'sya, ne imeet nichego obshchego s obychnymi effektami centrobezhnoj
sily. Relyativistskaya deformaciya ostaetsya neizmennoj, kak by sil'no ni byla
natyanuta nit', ne govorya uzhe o tom, chto obychnaya centrobezhnaya sila dejstvuet
v protivopolozhnom napravlenii.
Esli nablyudatel', nahodyashchijsya na platforme, vzdumaet proverit'
rezul'tat svoih postroenij, sravniv poluchennuyu "pryamuyu" s luchom sveta, to on
obnaruzhit, chto svet dejstvitel'no rasprostranyaetsya vdol' postroennoj im
linii. Razumeetsya, dlya nablyudatelej, stoyashchih u platformy, luch sveta voobshche
ne budet iskrivlen. Oni budut interpretirovat' rezul'taty dvizhushchegosya
nablyudatelya putem superpozicii, ili nalozheniya, vrashcheniya platformy i
pryamolinejnogo rasprostraneniya sveta. Oni skazhut vam, chto esli vy nanesete
carapinu na vrashchayushchuyusya grammofonnuyu plastinku, dvinuv rukoj po pryamoj, to
carapina na plastinke, konechno zhe, budet iskrivlennoj.
No dlya nablyudatelya, nahodyashchegosya na vrashchayushchejsya platforme, nazvanie
"pryamaya" dlya postroennoj im krivoj vpolne razumno: eta krivaya daet
_kratchajshee rasstoyanie_ i sovpadaet s _luchom sveta_ v sisteme otscheta nashego
nablyudatelya. Predpolozhim, chto on vybral na krayu platformy tri tochki i
soedinil ih pryamymi, postroiv tem samym treugol'nik. _Summa uglov v etom
treugol'nike men'she dvuh pryamyh_, iz chego nash nablyudatel' zaklyuchaet (i
sovershenno spravedlivo), chto prostranstvo vokrug nego iskrivleno.
Rassmotrim drugoj primer. Predpolozhim, chto dva drugih nablyudatelya na
platforme (|3 i |4) reshili ocenit' chislo pi, izmeryaya dlinu okruzhnosti
platformy i ee diametr. Na mernyj sterzhen' nablyudatelya |3 vrashchenie ne
vliyaet, poskol'ku dvizhenie sterzhnya vsegda perpendikulyarno ego dline. S
drugoj storony, mernyj sterzhen' nablyudatelya |4 vsegda budet sokrashchen, i dlya
dliny okruzhnosti platformy etot nablyudatel' poluchit bol'shee znachenie, chem v
sluchae nevrashchayushchejsya platformy. Delya rezul'tat, poluchennyj nablyudatelem 4,
na rezul'tat, poluchennyj nablyudatelem 3, my poluchim znachenie, prevyshayushchee
znachenie pi, obychno privodimoe v uchebnikah. |to takzhe yavlyaetsya sledstviem
krivizny prostranstva.
Vrashchenie vliyaet ne tol'ko na izmereniya dlin. CHasy, raspolozhennye na
krayu platformy, budut dvigat'sya s bol'shej skorost'yu i, kak bylo pokazano v
predydushchej lekcii, ih hod zamedlitsya po sravneniyu s hodom chasov,
ustanovlennyh v centre platformy.
Esli dva eksperimentatora (|4 i |5) sveryat chasy v centre platformy, a
zatem eksperimentator |5 na kakoe-to vremya otneset svoi chasy na kraj
platformy, to po vozvrashchenii v centr on obnaruzhit, chto ego chasy otstayut po
sravneniyu s chasami, vse vremya ostavavshimisya v centre platformy. Iz etogo
eksperimentator |5 sdelaet vyvod, chto v razlichnyh mestah platformy vse
fizicheskie processy idut s razlichnymi skorostyami. Predpolozhim teper', chto
nashi eksperimentatory ostanovilis' i nemnogo porazmyslili nad prichinoj
neobychnyh rezul'tatov, tol'ko chto poluchennyh imi v geometricheskih
izmereniyah. Predpolozhim takzhe, chto vrashchayushchayasya platforma zakryta so vseh
storon i predstavlyaet soboj vrashchayushchuyusya komnatu bez okon, chtoby
eksperimentatory ne mogli nablyudat' svoe dvizhenie otnositel'no okruzhayushchih
predmetov. Mogli by v etom sluchae eksperimentatory ob座asnit' vse poluchennye
rezul'taty chisto fizicheskimi usloviyami na platforme bez ucheta ee vrashcheniya
otnositel'no "tverdoj osnovy", na kotoroj ustanovlena platforma?
Glyadya na razlichiya mezhdu fizicheskimi usloviyami na platforme i na
"tverdoj osnove", posredstvom kotoryh mozhno bylo by ob座asnit' nablyudaemye
izmeneniya v geometrii, nashi eksperimentatory srazu zhe zametili by, chto
sushchestvuet kakaya-to novaya sila, kotoraya stremitsya otbrosit' vse tela ot
centra platformy k ee okruzhnosti. Vpolne estestvenno, chto oni pripisali by
nablyudaemye effekty dejstviyu etoj sily, utverzhdaya, naprimer, chto iz dvuh
chasov te budut idti medlennee, kotorye raspolozheny dal'she ot centra v
napravlenii novoj sily.
No dejstvitel'no li eta novaya sila nova, t. e. ne nablyudaema na
"tverdoj osnove"? Razve my ne nablyudaem, kak vse tela prityagivayutsya k centru
Zemli siloj, kotoraya poluchila nazvanie sily tyazhesti? Razumeetsya, v odnom
sluchae my imeem prityazhenie k okruzhnosti diska, v drugom - prityazhenie k
centru Zemli, no eto oznachaet tol'ko razlichie v raspredelenii sily.
Netrudno, odnako, privesti drugoj primer, kogda "novaya" sila, porozhdaemaya
neravnomernym dvizheniem sistemy otscheta, vyglyadit tochno tak zhe, kak sila
tyazhesti v etoj lekcionnoj auditorii.
Predpolozhim, chto kosmicheskij korabl', prednaznachennyj dlya mezhzvezdnyh
pereletov, svobodno letit gde-to v kosmicheskom prostranstve nastol'ko daleko
ot razlichnyh zvezd, chto vnutri korablya sila tyazhesti ne dejstvuet. Vse
predmety vnutri kosmicheskogo korablya i sami puteshestvuyushchie v nem
eksperimentatory nevesomy i svobodno plavayut v vozduhe primerno tak zhe, kak
Mishel' Ardan i ego sputniki vo vremya puteshestviya na Lunu v znamenitom romane
ZHyulya Verna.
No vot dvigateli vklyucheny i kosmicheskij korabl' prihodit v dvizhenie,
postepenno nabiraya skorost'. CHto proishodit vnutri nego? Netrudno videt',
chto poka kosmicheskij korabl' uskoryaetsya, vse predmety vnutri nego
obnaruzhivayut stremlenie dvigat'sya k polu, ili, chto to zhe, pol dvizhetsya
navstrechu etim predmetam. Naprimer, esli nash eksperimentator derzhit v ruke
yabloko i vypuskaet ego, to yabloko prodolzhaet dvigat'sya (otnositel'no
okruzhayushchih korabl' zvezd) s postoyannoj skorost'yu - toj samoj, s kotoroj
dvigalsya kosmicheskij korabl', kogda eksperimentator vypustil iz ruk yabloko.
No kosmicheskij korabl' uskoryaetsya. Sledovatel'no, pol kabiny, dvigayas' vse
bystree i bystree, v konce koncov dogonit yabloko i stuknet ego. S etogo
momenta yabloko ostanetsya v postoyannom kontakte s polom, buduchi prizhato k
polu postoyanno dejstvuyushchim uskoreniem.
No dlya eksperimentatora, nahodyashchegosya vnutri kosmicheskogo korablya, vse
vyglyadit inache: yabloko "padaet" s kakim-to uskoreniem i, udarivshis' ob pol,
ostaetsya lezhat' na polu, pridavlennoe k nemu sobstvennym vesom. Brosaya
razlichnye predmety, nash eksperiment