![\includegraphics [width=5cm]{Oto/SunAngel.eps}](img47.gif) |
Общая теория относительности является довольно молодой теорией. Так как она работает с самым слабым по силе взаимодействием (гравитационным), то эксперименты для ее подтверждения при существующем уровне экспериментальной техники в лабораторных условиях практически невозможны. Практически все имеющиеся на данный момент косвенные экспериментальные подтверждения теории пришли из астрофизики.
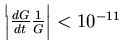 лет
лет
Одним из косвенных экспериментальных подтверждений ОТО является отклонение луча света в поле Солнца. Из эксперимента было получено, что электромагнитное поле взаимодействует с гравитационным полем. Схема эксперимента приведена на рис. 1. Мы точно знаем, когда звезда должна скрываться за Солнцем. Мы измеряем время, когда мы перестаем видеть эту звезду (эти эксперименты проводятся во время полных солнечных затмений), и извлекаем угол отклонения луча света от прямой. Из теории угол отклонения для Солнца равен:
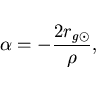 |
(5) |
где ![]() -- гравитационный
радиус Солнца (см. (3)),
-- гравитационный
радиус Солнца (см. (3)), ![]() -- прицельный параметр (в данной
постановке эксперимента он примерно равен радиусу Солнца).
-- прицельный параметр (в данной
постановке эксперимента он примерно равен радиусу Солнца).
Из эксперимента
![]() с точность около 0,3% (данные 1984 г.),
что полностью соответствует теории.
с точность около 0,3% (данные 1984 г.),
что полностью соответствует теории.
В принципе, отклонение луча в поле Солнца вытекает также и из ньютоновской корпускулярной теории света, но угол отклонения предсказывается ровно в два раза меньше, чем дает эксперимент.. Расчет для этой теории был проведен Зольдерном еще в 1804 году. Любопытно, что в своих расчетах Зольдерн сделал ошибку и получил "правильный" ответ с экспериментальной точки зрения (расчет был сделан до проведения эксперимента). Позже эту ошибку обнаружили.
Космический телескоп Хаббл (Hubble) сфотографировал объект, который представлял собой диск звезды (не Солнца), на краю которого была выемка. Была высказана гипотеза, что такое изображение возникло из-за того, что вокруг этой звезды вращается планета (массой от 0.1 до 10 масс Юпитера) и именно эта планета изменила траекторию лучей так, что в диске появилась выемка. Это не подтверждение ОТО, но показатель того, что взаимодействие луча света с гравитационным полем можно использовать как инструмент для исследования объектов, которых иным способом разглядеть невозможно.
Теория предсказывает изменение частоты (красное смещение) ![]() при распространении
между точками 1 и 2, разность гравитационных потенциалов между которыми равна
при распространении
между точками 1 и 2, разность гравитационных потенциалов между которыми равна
![]() ,
где
,
где ![]() -- ускорение свободного падения,
-- ускорение свободного падения,
![]() -- перепад высот между точками 1 и 2. Это верно если мы проводим
эксперимент в лабораторных условиях, то есть перепад высот мал по
сравнению с радиусом Земли (
-- перепад высот между точками 1 и 2. Это верно если мы проводим
эксперимент в лабораторных условиях, то есть перепад высот мал по
сравнению с радиусом Земли (
![]() )
)
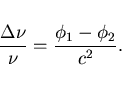 |
(6) |
Эксперименты в лаборатории подтвердили эту формулу с точностью
1% (для регистрации изменения частоты использовался
эффект Мессбауэра), а с помощью водородного мазера, установленного на
ракете, точность доведена до ![]() от предсказываемой
величины (1980).
от предсказываемой
величины (1980).
Еще один косвенный эксперимент, подтверждающий ОТО -- запаздывание сигнала в поле Солнца. Схема эксперимента показана на рис. 2. Сигнал посылается на Венеру и регистрируется время прихода сигнала обратно. Значение времени прохождения сигнала туда и обратно в поле Солнца (гравитационный объект искажает пространство-время) отличается от значения если бы Солнца не было (свободное пространство -- нет искажений). Время задержки сигнала из теории примерно равно
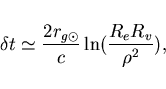 |
(7) |
где ![]() -- гравитационный
радиус Солнца (см. 3),
-- гравитационный
радиус Солнца (см. 3), ![]() -- радиус орбиты Земли,
-- радиус орбиты Земли,
![]() -- радиус орбиты Венеры,
-- радиус орбиты Венеры, ![]() -- прицельный параметр,
-- прицельный параметр,
![]() -- скорость света.
-- скорость света.
Из эксперимента
![]() с с точностью до 0,1%,
что полностью соответствует теории.
с с точностью до 0,1%,
что полностью соответствует теории.
Эксперименты проводились с помощью радиолокации планет Меркурий и Венера во время их прохождения за диском Солнца, а также с помощью ретрансляции радиолокационных сигналов космическими кораблями, в том числе кораблями, движущимися вокруг планеты Марс.
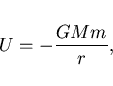 |
(8) |
где ![]() -- расстояние между взаимодействующими телами массы
-- расстояние между взаимодействующими телами массы ![]() и
и ![]() ,
,
![]() -- гравитационная постоянная.
-- гравитационная постоянная.
Существует лишь два типа центральных полей, в которых все траектории
финитных (тело не уходит на бесконечность) движений замкнуты.
Это поля, в которых потенциальная энергия
частицы пропорциональна
![]() или
или ![]() (для
подробного объяснения смотрите [3], параграф 14, "Движение
в центральном поле").
(для
подробного объяснения смотрите [3], параграф 14, "Движение
в центральном поле").
Есть несколько причин смещения перигелия (точка максимального сближения тел), но их суммарный вклад недает совпадения теории с экспериментом. ОТО дает недостающую поправку.
Из-за того, что Солнце массивный объект, пространство искривлено,
а так как планеты двигаются по эллипсам (то приближаются, то удаляются),
то зависимость потенциальной энергии от радиуса
![]() нарушается (она переходит в зависимость
нарушается (она переходит в зависимость
![]() )
и орбита планеты перестает быть замкнутой.
)
и орбита планеты перестает быть замкнутой.
Самый удобный объект для исследований -- Меркурий -- он ближе всех к Солнцу.
Угол смещения перигелия за один оборот равен:
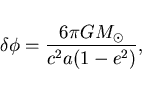 |
(9) |
За 100 лет смещение перигелия Меркурия составило
![]() ,
а по теории это смещение равно
,
а по теории это смещение равно ![]() -- потрясающая точность.
-- потрясающая точность.
Ниже идут теоретические и экспериментальные значения угла смещения перигелия за 100 лет еще для некоторых небесных тел:
| Смещение перигелия за 100 лет | ||
| Планета | Эксперимент | Теория |
| Меркурий |
|
|
| Венера |
|
|
| Икарус | ||
| Земля | ||
Так как лучи света искривляются в поле Солнца, то, вероятно, массивные
объекты можно использовать как линзы. Схема эксперимента приведена на
рис. 3. Наблюдатель находится в точке O, в точке
A находится источник света (например, галактика). Если
в точке C находится массивный гравитационный объект (туманность,
галактика или другое массивное тело), то из-за искривления хода луча,
нам будет казаться, что наблюдаемый удаленный объект находится в точке
B, то есть мы его как бы увеличиваем. Этот эффект называется
гравитационным линзированием. Он наблюдаем только в том
случае, если масса гравитационной линзы порядка ![]() масс Солнца
и больше.
масс Солнца
и больше.
Конечно, гравитационная линза своим поведением сильно отличается от оптической в силу того, что теория гравитации принципиально нелинейна. Если бы удаленный объект находился на линии наблюдатель -- линза, то наблюдатель увидел бы кольцо (на рис. 3 справа выделено пунктиром) -- кольцо Эйнштейна. Вероятность подобного совпадения мала (мы не имеем возможностей изменять какую либо из базовых точек), точечный источник будет виден как две дуги (на рис. 3 справа) внутри и снаружи относительно кольца Эйнштейна. Впервые подобный объект был обнаружен в 1979 году. Он выглядел как две туманности с абсолютно одинаковым спектром излучения. Сейчас ведется поиск подобных объектов. Серьезно изучается вопрос о наблюдении структуры галактик с помощью этого эффекта.
С помощью подобного эффекта (гравитационного микролинзрования -- масса гравитационной линзы очень мала) были обнаружены коричневые карлики. Коричневые карлики -- это невидимые объекты не очень большой (по звездным меркам) массы. Если какой-либо коричневый карлик встанет на линию наблюдатель -- яркий объект, то наблюдается изменение яркости объекта. Коричневый карлик играет роль линзы. По изменению яркости и расстоянию до наблюдаемого объекта можно грубо оценить массу гравитационной линзы. Эти оценки показывают, что наблюдаемые таким образом объекты являются коричневыми карликами.
На данный момент не существует других способов зарегистрировать темный объект, кроме как использовать эффект гравитационной линзы.
Известно, что электромагнитное взаимодействие квантуется. Существуют
частицы -- ![]() -кванты, которые переносят это взаимодействие.
-кванты, которые переносят это взаимодействие.
![]() -кванты -- это фотоны из которых состоит луч света. Эйнштейн хотел
написать общую теорию взаимодействия, которая объединила бы все
известные типы взаимодействия в одно. Логично
предположить, что существует некая частица, которая переносит
гравитационное взаимодействие (следует отметить, что сам Эйнштейн
был противником квантовой механики). Если есть кванты
взаимодействия, то есть и гравитационное излучение. Очень заманчиво
научиться делать приемники, которые улавливают это излучение,
так как в этом случае мы получили бы еще один инструмент изучения
Вселенной.
-кванты -- это фотоны из которых состоит луч света. Эйнштейн хотел
написать общую теорию взаимодействия, которая объединила бы все
известные типы взаимодействия в одно. Логично
предположить, что существует некая частица, которая переносит
гравитационное взаимодействие (следует отметить, что сам Эйнштейн
был противником квантовой механики). Если есть кванты
взаимодействия, то есть и гравитационное излучение. Очень заманчиво
научиться делать приемники, которые улавливают это излучение,
так как в этом случае мы получили бы еще один инструмент изучения
Вселенной.
Попытки создать подобный приемник предпринимаются в данное время, но гравитационные волны на существующих установках (MAUTIGUS, AURIGA, EXPLORER -- название работающих установок) не обнаружены, что не удивительно, слишком уж гравитационное взаимодействие слабое.
Существуют другой, косвенный метод проверки гипотезы о существовании гравитационного излучения. В великолепном учебнике [4], написанном Л.Д. Ландау и Е.М. Лифшицом, в параграфе 110 "Излучение гравитационных волн" была предложена и разобрана задача:
Задача: Два тела, притягивающиеся по закону Ньютона, движутся по круговым орбитам (вокруг их общего центра инерции). Определить среднюю (по периоду обращения) интенсивность излучения гравитационных волн.
Если предположить, что такой объект существует, то из-за потери энергии на гравитационное излучение происходит постепенное (как говорят вековое) сближение тел, а следовательно и увеличение частоты вращения. Скорость изменения частоты вращения двойной звезды со временем равна:
где ![]() -- угловая частота вращения двойной системы вокруг общего
центра масс,
-- угловая частота вращения двойной системы вокруг общего
центра масс, ![]() -- гравитационная постоянная,
-- гравитационная постоянная, ![]() и
и ![]() -- массы
вращающихся тел,
-- массы
вращающихся тел, ![]() -- расстояние между телами.
-- расстояние между телами.
Коэффициент перед ![]() весьма нетривиален. Если она верна, то это сильный
довод в пользу существования гравитационных волн.
весьма нетривиален. Если она верна, то это сильный
довод в пользу существования гравитационных волн.
Несколько лет назад были опубликованы результаты (Тэйлор и Кол -- они получили за это Нобелевскую премию) наблюдения одного астрофизического объекта (изучение движения пульсара PSR 1913+16 в двойной системе). Объект представлял из себя систему двойной звезды. Партнеры в этой системы очень сильно отличались друг от друга (в паре есть пульсар). За этим объектом велись наблюдения в течении 14 лет (1975-89) -- он был очень хорошо изучен. Было обнаружено, что со временем период вращения уменьшается. Результаты были обработаны и полностью (с точностью до 1%) совпали с теорией (скорость изменения угловой частоты вращения полностью совпала с результатом формулы (10)). При опубликовании результатов авторы ссылались на задачу в учебнике Ландау -- Лифшица. Вся теория была взята именно оттуда. На данный момент ведется очень активный поиск подобных объектов (по крайней мере, найдено еще два таких объекта).