Vopros: CHto takoe demon Maksvella?
Otvet: Vot takoe opredelenie demona Maksvella dano v izvestnom bestsellere "Ponedel'nik nachinaetsya v subbotu" Arkadiya i Borisa Strugackih: Demon Maksvella -- vazhnyj element myslennogo eksperimenta krupnogo anglijskogo fizika Maksvella. Prednaznachalsya dlya napadeniya na vtoroj princip termodinamiki. V myslennom eksperimente Maksvella demon raspolagalsya ryadom s otverstiem v pereborke, razdelyayushchej sosud, napolnennyj dvizhushchimisya molekulami. Rabota demona sostoit v tom, chtoby vypuskat' iz odnoj poloviny sosuda v druguyu bystrye molekuly i zakryvat' otverstiya pered nosom medlennyh. Ideal'nyj demon sposoben takim obrazom bez zatraty truda sozdat' ochen' vysokuyu temperaturu v odnoj polovine sosuda i ochen' nizkuyu -- v drugoj, osushchestvlyaya vechnyj dvigatel' vtorogo roda. Odnako tol'ko sravnitel'no nedavno i tol'ko v nashem institute (imeetsya v vidu NIICHAVO -- Nauchno-Issledovatel'skij Institut CHArodejstva i VOlshebstva) udalos' najti i prisposobit' k rabote takih demonov.
Teper' po poryadku: Vtoroe nachalo termodinamiki bylo sformulirovano R. Klauziusom v 1850 godu: "Nevozmozhen process, pri kotorom teplota perehodila by samoproizvol'no ot tel bolee holodnyh k telam bolee nagretym". Vtoroe nachalo termodinamiki isklyuchaet vozmozhnost' sozdaniya vechnyh dvigatelej vtorogo roda -- mashin nepreryvnogo dejstviya, sposobnyh prevrashchat' v poleznuyu rabotu vsyu podvodimuyu k nim teplotu (obhodit'sya tol'ko nagrevatelem i ne ispol'zovat' holodil'nik pri svoej rabote).
Seredina XIX veka -- eto vremya, kogda proishodila lomka stereotipov. Na mesto prichinnyh dinamicheskih zakonov stanovyatsya statisticheskie zakony, pozvolyayushchie predvidet' evolyuciyu prirody ne s absolyutnoj tochnost'yu, a lish' s bol'shoj stepen'yu veroyatnosti. Dlya togo chtoby pokazat', chto vtoroe nachalo termodinamiki ne yavlyaetsya absolyutnym (neprelozhnym i vsegda vypolnimym) zakonom prirody na scenu poyavilsya myslennyj eksperiment s demonom Maksvella (1871 g.).
Demon rabotaet takim obrazom, chto odna chast' sosuda samoproizvol'no nagrevaetsya, a drugaya ohlazhdaetsya -- eto narushaet vtoroe nachalo termodinamiki. Preodolenie trudnostej s narusheniem vtorogo nachala potrebovalo ot Bol'cmana radikal'nogo novovvedeniya: vtoroe nachalo termodinamiki rassmatrivaetsya ne kak dostovernyj zakon prirody (kotoryj taki narushaetsya s pomoshch'yu demonov Maksvella), a kak v vysshej stepeni veroyatnyj.
Dopustim u nas est' rezervuar s goryachimi (![]() shtuk)
i holodnymi (
shtuk)
i holodnymi (![]() shtuk) molekulami (gaz ideal'nyj
i vzaimodejstviya mezhdu molekulami ne proishodit).
My ego ostavili na dlitel'noe vremya. Myslenno podelim rezervuar
popolam. Veroyatnost' togo chto holodnaya molekula okazhetsya v pravoj
polovine ravna
shtuk) molekulami (gaz ideal'nyj
i vzaimodejstviya mezhdu molekulami ne proishodit).
My ego ostavili na dlitel'noe vremya. Myslenno podelim rezervuar
popolam. Veroyatnost' togo chto holodnaya molekula okazhetsya v pravoj
polovine ravna ![]() (podelili popolam), to zhe samoe mozhno skazat'
i pro veroyatnost' dlya goryachej molekuly okazat'sya v levoj polovine.
Veroyatnost' togo, chto vse goryachie molekuly soberutsya sleva, a vse holodnye
sprava, est' prosto proizvedenie veroyatnostej i ravno:
(podelili popolam), to zhe samoe mozhno skazat'
i pro veroyatnost' dlya goryachej molekuly okazat'sya v levoj polovine.
Veroyatnost' togo, chto vse goryachie molekuly soberutsya sleva, a vse holodnye
sprava, est' prosto proizvedenie veroyatnostej i ravno:
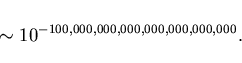
CHem zhe zanimalis' demony Maksvella v NIICHAVO: "Demony igrali v samuyu stohasticheskuyu iz igr -- v orlyanku... Odin vyigryval, a drugoj, sootvetstvenno, proigryval, i eto ih bespokoilo, tak kak narushalo statisticheskoe ravnovesie."
Rekomenduemaya literatura: Mario L'occi "Istoriya Fiziki", Fizicheskij |nciklopedicheskij slovar'.
Ochen' rekomenduemaya literatura: "Ponedel'nik nachinaetsya v subbotu" -- skazka dlya nauchnyh rabotnikov mladshego vozrasta, Arkadij i Boris Strugackie.