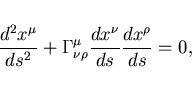 |
(1) |
Vopros: V chem zaklyuchaetsya uslozhnennyj variant teorii otnositel'nosti?
Pod uslozhnennym variantom, po vidimomu, podrazumevaetsya obshchaya teoriya otnositel'nosti (OTO). |jnshtejn (A. Einstein), kak izvestno, pytalsya postroit' obshchuyu teoriyu iz kotoroj by sledovali vse vzaimodejstviya, no ne preuspel. Nazvanie "Obshchaya teoriya otnositel'nosti" prinadlezhit |jnshtejnu. |to nazvanie yavlyaetsya neadekvatnym i postepenno ischezaet iz literatury, zamenyayas' na "teoriyu tyagoteniya" [1].
Postroenie OTO |jnshtejn nachal v 1907 godu i zakonchil vmeste H.D. Gil'bertom (H.D Hilbert) v 1915. Bol'shoj vklad v razvitie matematicheskogo apparata teorii vnes v 1908-10 godah G. Minkovskij (H. Minkowski).
V osnove OTO lezhit eksperimental'nyj fakt ravenstva inertnoj massy (vhodyashchej vo 2-oj zakona N'yutona) i gravitacionnoj massy (vhodyashchej v zakon tyagoteniya) dlya lyubogo tela. |to ravenstvo proyavlyaetsya v tom, chto dvizhenie tela v pole tyagoteniya ne zavisit ot ego massy. Sledstviem etogo yavlyaetsya otsutstvie gravitacionno nejtral'nyh tel.
V rabote, sdelannoj v 1907 g., |jnshtejn predlozhil myslennyj eksperiment [2]: predstavim sebe gigantskij neboskreb vysotoj 1000 km i fizika, nahodyashchegosya vnutri svobodno padayushchego lifta v etom neboskrebe. Fizik vypuskaet iz ruk platok i chasy i ubezhdaetsya, chto oni ne padayut na pol lifta. Esli on soobshchaet etim veshcham tolchok, to oni dvizhutsya ravnomerno i pryamolinejno, poka ne stolknutsya so stenkami lifta. Fizik prihodit k vyvodu: ya nahozhus' v ogranichennoj galileevoj sisteme. Uslovie ogranichennosti neobhodimo dlya togo, chtoby mozhno bylo schitat', chto vse tela ispytyvayut odinakovoe uskorenie. No fizik, nablyudayushchij izvne za padeniem lifta, budet sudit' o veshchah sovershenno inache. On vidit, chto lift i vse nahodyashcheesya v nem dvizhutsya uskorenno v sootvetstvii s zakonom tyagoteniya N'yutona.
|tot primer pokazyvaet, chto mozhno perejti ot galileevoj sistemy k uskorennoj, esli uchest' gravitacionnoe pole. Inymi slovami gravitacionnoe pole (v kotorom proyavlyaetsya gravitacionnaya massa) ekvivalentno uskorennomu dvizheniyu (v kotorom proyavlyaetsya inertnaya massa). Gravitacionnaya massa i inertnaya massa harakterizuyut odno i to zhe svojstvo materii, rassmatrivaemoe po-raznomu (raznost' massy sovremennymi eksperimental'nymi metodami ne obnaruzhena). Takim obrazom, |jnshtejn prishel k principu ekvivalentnosti, kotoryj on tak sformuliroval v svoej avtobiografii:
V pole tyagoteniya (maloj prostranstvennoj protyazhennosti) vse proishodit tak, kak v prostranstve bez tyagoteniya, esli v nem vmesto "inercial'noj" sistemy otscheta vvesti sistemu, uskorennuyu otnositel'no nee.
Dannyj princip pozvolyaet traktovat' tyagotenie kak iskrivlenie prostranstva-vremeni.
Iskrivlenie prostranstva-vremeni harakterizuetsya simvolami Kristofelya.
Esli vse simvoly Kristofelya ravny 0, chto sootvetstvuet
otsutstviyu gravitacionnogo polya, to uravnenie geodezicheskoj
perehodit v uravnenie pryamoj ![]() ,
gde
,
gde
![]() --
uskorenie tela, to est' my poluchaem pervyj zakon N'yutona.
V priblizhenii N'yutona geodezicheskimi liniyami yavlyayutsya pryamye.
--
uskorenie tela, to est' my poluchaem pervyj zakon N'yutona.
V priblizhenii N'yutona geodezicheskimi liniyami yavlyayutsya pryamye.
Podrobno matematicheskij apparat i vyvody sledstvij obshchej teorii otnositel'nosti opisany v [4].
|to vyrazhenie otlichaetsya ot N'yutonovskogo vyrazheniya dlya uskoreniya kornem
v znamenatele. Velichina ![]() stremitsya k beskonechnosti, kogda
stremitsya k beskonechnosti, kogda ![]() stremitsya
k
stremitsya
k
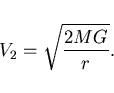 |
(4) |
Teoreticheskaya astrofizika predskazyvaet vozniknovenie chernyh dyr v konce evolyucii massivnyh zvezd; vozmozhno sushchestvovanie chernyh dyr i drugogo proishozhdeniya (reliktovye chernye dyry -- ostatki posle "bol'shogo vzryva"). Na dannyj moment astronomy nablyudayut ob®ekty, kotorye predstavlyayut iz sebya dvojnye zvezdnye sistemy, v sostav kotoryh (kak predpolagaetsya) vhodyat chernye dyry.